人教版 必修第一册 2.3匀变速直线运动的位移与时间的关系(共37张PPT)
文档属性
| 名称 | 人教版 必修第一册 2.3匀变速直线运动的位移与时间的关系(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-30 09:42:28 | ||
图片预览










文档简介
(共37张PPT)
专题四 运动图像及追及相遇问题
概念(y=kx+b)
k:斜率(直线的倾斜程度) 大小:看陡平
正负:看上下 计算:k=
(x1,y1)
(x2,y2)
(x1,y1)
(x2,y2)
x-t图像中直线的或曲线的切线的斜率表示速度(位置变化率)
v-t图像中直线的或曲线的切线的斜率表示加速度(速度变化率)
物体运动方向与速度方向相同
k>0,v>0,运动方向为正
k<0,v<0,运动方向为负
速度在t轴上为正(v>0),在t轴下为负(v<0)
远离t轴为加速,靠近t轴为减速
k>0,a>0,加速度方向为正
k<0,a<0,加速度方向为负
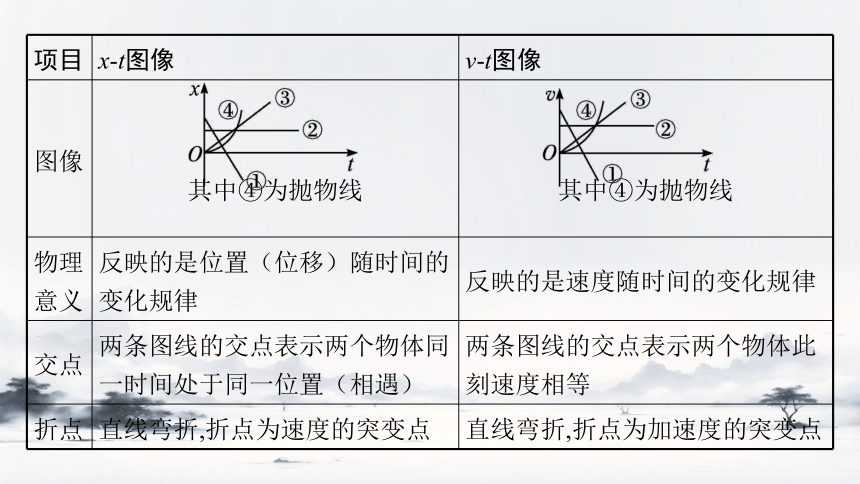
知识点一 x-t图像与v-t图像的区别
在物理学中,图像法是一种十分重要的方法,用图像法分析和解决物理问题往往比用解析法更简洁直观。运动学中,位移—时间图像(x-t图像)和速度—时间图像(v-t图像)是两种最典型的图像。这两种图像里包含了大量的信息,考试时可能会从各个方面考查,下面我们进行具体全面的描述。
项目 x-t图像 v-t图像
图像 其中④为抛物线
其中④为抛物线
物理 意义 反映的是位置(位移)随时间的变化规律 反映的是速度随时间的变化规律
交点 两条图线的交点表示两个物体同一时间处于同一位置(相遇) 两条图线的交点表示两个物体此刻速度相等
折点 直线弯折,折点为速度的突变点 直线弯折,折点为加速度的突变点
项目 x-t图像 v-t图像
线 (1)倾斜直线表示物体做匀速直线运动 (2)图像为曲线时,物体做变速直线运动 (3)图像平行于时间轴表示物体静止 (1)倾斜直线表示物体做匀变速直线运动
(2)图像为曲线时,物体做变速直线运动
(3)图像平行于时间轴表示物体做匀速直线运动
截距 (1)纵坐标截距表示t=0时刻的位移 (2)横坐标截距表示物体位置坐标为零的时刻 (1)纵坐标截距表示t=0时刻的速度
(2)横坐标截距表示速度为零的时刻
项目 x-t图像 v-t图像
斜率 描述速度:斜率的大小表示速度的大小,斜率的正负表示速度的方向 描述加速度:斜率的大小表示加速度的大小,斜率的正负表示加速度的方向
面积 无实际意义 (1)横轴上方的图线表示速度的方向为正方向,故在横轴上方围成的面积为正,表示质点通过的位移为正方向
(2)横轴下方的图线表示速度的方向为负方向,在横轴下方围成的面积为负,表示位移为负方向
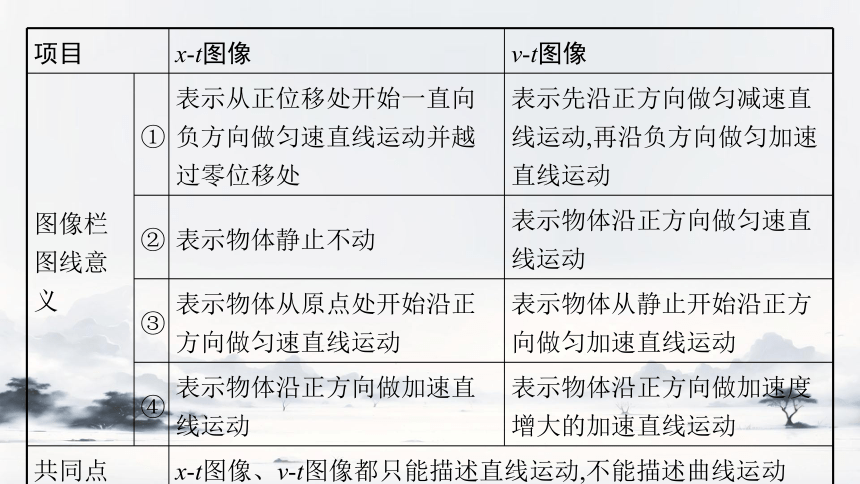
项目 x-t图像 v-t图像
图像栏图线意义 ① 表示从正位移处开始一直向负方向做匀速直线运动并越过零位移处 表示先沿正方向做匀减速直线运动,再沿负方向做匀加速直线运动
② 表示物体静止不动 表示物体沿正方向做匀速直线运动
③ 表示物体从原点处开始沿正方向做匀速直线运动 表示物体从静止开始沿正方向做匀加速直线运动
④ 表示物体沿正方向做加速直线运动 表示物体沿正方向做加速度增大的加速直线运动
共同点 x-t图像、v-t图像都只能描述直线运动,不能描述曲线运动 【例1】 (多选)甲、乙两物体同时同地沿同一方向做直线运动,甲的x-t图像和乙的v-t图像如图所示,下列说法正确的是( )
A.0~2 s内,甲、乙两物体之间的距离一直增大
B.第3 s内,甲、乙两物体速度方向相反
C.2~4 s内,甲、乙均做减速运动
D.6 s末,甲、乙两物体均回到原出发点
BD
方法技巧 v-t图像和x-t图像的应用技巧
(1)确认是哪种图像,究竟是v-t图像还是x-t图像。
(2)理解并熟记五个对应关系
①斜率与加速度或速度对应;
②纵截距与初速度或初始位置对应;
③横截距对应速度或位移为零的时刻;
④交点对应速度或位置相同;
⑤拐点对应运动状态发生改变。
例2.ETC是高速公路上电子不停车收费系统的简称。一辆汽车在进入ETC通道入口前减速到以54 km/h的速度匀速行驶,在进入ETC通道入口时速度减为18 km/h,匀速到达自动栏杆处,在通道内,ETC已完成车辆信息识别同时自动栏杆抬起,汽车通过自动栏杆之后,立刻加速到原来的速度,这一过程中其v-t图像如图所示,则( )
知识点二 非常规图像及应用
1.a-t图像中的五点信息
线 截距 交点 斜率 面积
(1)倾斜直线表示变加速直线运动; (2)平行于横轴的直线表示匀变速直线运动 纵截距表示t=0时的加速度 表示两物体该时刻加速度相同 过某点直线(或切线)的斜率表示加速度变化的快慢 表示物体的速度变化量
2.利用a-t图像求末速度:已知某段时间的初速度v0,求出a-t图像与坐标轴所围面积Δv,则这段时间的末速度v=v0+Δv。
3.v2-x图像中的四点信息
线 截距 交点 斜率
倾斜直线表 示匀变速直 线运动 纵截距表示初速度的二次方 表示两物体该时刻速度的二次方相等 表示加速度的2倍
【例3】 (多选)无人驾驶汽车作为汽车的前沿科技,目前尚在完善中,它车头装有一个激光雷达,就像车辆的“鼻子”,随时“嗅”着前方88 m范围内车辆和行人的“气息”,制动反应时间为0.2 s,比有人驾驶汽车平均快1 s。如图所示为在某次测试场地进行制动测试时获得的一部分图像(v为汽车的速度,x为位置坐标)。关于该无人驾驶汽车在该路段的制动测试,下列说法正确的是( )
A.制动加速度大小为10 m/s2
B.以30 m/s的速度匀速行驶时,从“嗅”到前方行人
“气息”到停止需要3 s
C.以30 m/s的速度匀速行驶时,从“嗅”到前方行人
“气息”到停止的距离为51 m
D.最大安全速度是40 m/s
ACD
例4.(2023山东济南高一期末)如图所示,小勤用手机传感器记录了一段时间内某汽车加速度随时间变化的图像。设汽车前进的方向为正方向,已知小勤计时的零时刻汽车仪表盘显示车速为72 km/h。根据所学知识分析,以下说法正确的是( )
A.第5 s末汽车的速度约为12 m/s
B.第7 s末汽车速度为负,此时该汽车可能正在倒车
C.第7 s末汽车的速度约为16 m/s
D.汽车在2~5 s内位移小于5~7 s内位移
C
2
5
7
16
20
32
知识点三 追及和相遇问题
1.对“相遇”“追及”的认识
(1)相遇问题
两个物体(均可看成质点)在同一直线上运动,当它们同时到达同一位置时,即相遇。
①如图所示,若两个物体相向运动,则二者位移大小之和等于开始时两物体间的距离,即xA+xB=x0时相遇。
A
B
②如图所示,若两个物体同向运动,则二者位移大小之差等于开始时两物体间的距离,即xA-xB=x0时相遇。
(2)追及问题
同向运动的物体,若后者能追上前者,则追上时,两者处于同一位置,且后者的速度不小于前者的速度。
B
A
2.追及相遇问题中的一个条件和两个关系
(1)一个条件:即两者速度相等,它往往是物体间能够追上、追不上或两者距离最大、最小的临界条件,也是分析判断的切入点。
(2)两个关系:即两者时间关系和位移关系,这两个关系可通过画两者的运动示意图得到。
对点训练一
3.追及相遇问题常见的情况
假设物体A追物体B,开始时两个物体相距x0,有三种常见情况:
(1)若vA=vB时,xA≥xB+x0,则A追上B;若xA=xB+x0时,vA≥vB,则A追上B。若vA=vB时,xA(2)要使两物体恰好不相撞,两物体同时到达同一位置时速度相同,即vA=vB时,xA=x0+xB,则A与B恰好不相撞。
(3)若使两物体不相撞,则要求当vA=vB时,xA(4)若被追赶的物体做匀减速直线运动,一定要注意判断追上前该物体是否已经停止运动。
4.四种常用方法
物理分 析法 建立两物体运动的情境并画出示意图,找出两物体的位移、速度及时间关系,选择公式列方程求解
函数法 设两物体在t时刻相遇,然后根据位移关系列出关于t的方程f(t)=0,若方程f(t)=0无正实数解,则说明这两个物体不可能相遇;若方程f(t)=0存在正实数解,说明这两个物体能相遇
图像法 ①若用x-t图像求解,分别作出两物体的x-t图像,如果两物体的位移—时间图线相交,则说明两物体相遇;②若用v-t图像求解,则注意比较图线与时间轴所围图形的面积
相对运 动法 取其中一个运动物体为参考系,分析另一个物体相对它的运动,当两者的相对位移为零时相遇,计算时需要将速度、位移、加速度都转换为相对速度、相对位移、相对加速度代入公式
5.解题思路流程
对点训练三
【例5】 一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车的旁边通过,运动方向与汽车相同。试求:
(1)汽车在追上自行车前与自行车相距最远时的运动时间以及此时两者间的距离。
(2)汽车追上自行车所用时间和追上自行车时汽车的瞬时速度。
汽车
自行车
解析 (1)方法一:物理分析法
汽车与自行车的速度相等时两车相距最远,设此时经过的时间为t1,汽车的速度为v1,两车间的距离为Δx,则有v1=at1=v自
汽车与自行车相距的最远距离为
方法二:图像法
自行车和汽车运动的v-t图像如图所示,由图可以看出,在相遇前,t1时刻两车速度相等,两车相距最远,此时的距离为阴影三角形的面积,
方法三:函数法
设汽车在追上自行车之前经过时间t1两车相距最远,则
由二次函数求极值的条件知t1=2 s时,Δx最大
所以Δx=6 m。
(2)方法一:当两车位移相等时,汽车追上自行车,设此时经过的时间为t2,汽车的瞬时速度为v2,则有
v2=at2=3×4 m/s=12 m/s。
方法二:由图可以看出,在t1时刻之后,由图线v自、v汽和t=t2构成的三角形的面积与标有阴影的三角形面积相等,此时汽车与自行车的位移相等,即汽车与自行车相遇。由几何关系知t2=2t1=4 s
v2=at2=3×4 m/s=12 m/s。
方法技巧 追及问题常用的临界条件
(1)速度小者(但加速度大)追速度大者(但加速度小),追上前两个物体速度相等时,有最大距离。
(2)速度大者追速度小者,若不能追上,则两个物体速度相等时,有最小距离。即必须在此之前追上,否则就追不上。
例6.图a为马拉松比赛中两位参赛选手的某一情形,甲、乙两人起跑时都做匀加速直线运动,达到某一速度后都各自做匀速直线运动直至终点,他们的速度—时间图像如图b所示,则下列说法正确的是( )
A.乙选手起跑2 s后刚好追上甲选手
B.乙选手起跑时,甲选手正好跑了3 m
C.相遇前甲、乙两选手之间的最大距离为4 m
D.乙选手超过甲选手后,两选手可能再次相遇
C
1.(用图像分析追击相遇问题)(2023广东广州高一期末)某兴趣小组举行机器人跑步比赛,甲、乙两机器人均做直线运动。两机器人运动的位移—时间图像如图所示,其中机器人乙的x-t图线是关于x轴对称的抛物线的一部分,则下列说法正确的是( )
A.机器人甲先做匀减速直线运动后做匀速直线运动
B.机器人甲在0~10 s内的平均速度为-1.5 m/s
C.机器人乙一定做初速度为零的匀加速直线运动
D.在0~10 s内甲、乙机器人相遇两次,且相遇时速度可能相等
C
2.(追及相遇问题)甲车以3 m/s2的加速度由静止开始做匀加速直线运动,乙车落后2 s在同一地点由静止出发,以4 m/s2的加速度做匀加速直线运动,两车速度方向一致。在乙车追上甲车之前,两车距离的最大值是( )
A.18 m B.24 m C.22 m D.28 m
B
3.(v-t图像的应用)物体a、b从同一位置沿同一直线运动的v-t图像如图所示,下列说法正确的是( )
A.t=2 s时,a、b的速度方向均发生改变
B.t=4 s时,a、b相距20 m
C.前4 s,a、b均做匀变速直线运动
D.前4 s,a与b的加速度始终相同
B
4.(a-t图像的应用)(2023安徽阜阳高一月考)某同学正用遥控器控制一架无人机运送物体,t=0时物体的速度向上,且为1 m/s,取竖直向上为正方向,无人机的加速度随时间变化的关系图像如图所示,则下列说法正确的是( )
A.在0~1 s内物体做匀加速直线运动
B.物体在1 s末的速度为3 m/s
C.1 s末物体开始向下运动
D.0~3 s内,3 s末物体离地面最远
D
专题四 运动图像及追及相遇问题
概念(y=kx+b)
k:斜率(直线的倾斜程度) 大小:看陡平
正负:看上下 计算:k=
(x1,y1)
(x2,y2)
(x1,y1)
(x2,y2)
x-t图像中直线的或曲线的切线的斜率表示速度(位置变化率)
v-t图像中直线的或曲线的切线的斜率表示加速度(速度变化率)
物体运动方向与速度方向相同
k>0,v>0,运动方向为正
k<0,v<0,运动方向为负
速度在t轴上为正(v>0),在t轴下为负(v<0)
远离t轴为加速,靠近t轴为减速
k>0,a>0,加速度方向为正
k<0,a<0,加速度方向为负
知识点一 x-t图像与v-t图像的区别
在物理学中,图像法是一种十分重要的方法,用图像法分析和解决物理问题往往比用解析法更简洁直观。运动学中,位移—时间图像(x-t图像)和速度—时间图像(v-t图像)是两种最典型的图像。这两种图像里包含了大量的信息,考试时可能会从各个方面考查,下面我们进行具体全面的描述。
项目 x-t图像 v-t图像
图像 其中④为抛物线
其中④为抛物线
物理 意义 反映的是位置(位移)随时间的变化规律 反映的是速度随时间的变化规律
交点 两条图线的交点表示两个物体同一时间处于同一位置(相遇) 两条图线的交点表示两个物体此刻速度相等
折点 直线弯折,折点为速度的突变点 直线弯折,折点为加速度的突变点
项目 x-t图像 v-t图像
线 (1)倾斜直线表示物体做匀速直线运动 (2)图像为曲线时,物体做变速直线运动 (3)图像平行于时间轴表示物体静止 (1)倾斜直线表示物体做匀变速直线运动
(2)图像为曲线时,物体做变速直线运动
(3)图像平行于时间轴表示物体做匀速直线运动
截距 (1)纵坐标截距表示t=0时刻的位移 (2)横坐标截距表示物体位置坐标为零的时刻 (1)纵坐标截距表示t=0时刻的速度
(2)横坐标截距表示速度为零的时刻
项目 x-t图像 v-t图像
斜率 描述速度:斜率的大小表示速度的大小,斜率的正负表示速度的方向 描述加速度:斜率的大小表示加速度的大小,斜率的正负表示加速度的方向
面积 无实际意义 (1)横轴上方的图线表示速度的方向为正方向,故在横轴上方围成的面积为正,表示质点通过的位移为正方向
(2)横轴下方的图线表示速度的方向为负方向,在横轴下方围成的面积为负,表示位移为负方向
项目 x-t图像 v-t图像
图像栏图线意义 ① 表示从正位移处开始一直向负方向做匀速直线运动并越过零位移处 表示先沿正方向做匀减速直线运动,再沿负方向做匀加速直线运动
② 表示物体静止不动 表示物体沿正方向做匀速直线运动
③ 表示物体从原点处开始沿正方向做匀速直线运动 表示物体从静止开始沿正方向做匀加速直线运动
④ 表示物体沿正方向做加速直线运动 表示物体沿正方向做加速度增大的加速直线运动
共同点 x-t图像、v-t图像都只能描述直线运动,不能描述曲线运动 【例1】 (多选)甲、乙两物体同时同地沿同一方向做直线运动,甲的x-t图像和乙的v-t图像如图所示,下列说法正确的是( )
A.0~2 s内,甲、乙两物体之间的距离一直增大
B.第3 s内,甲、乙两物体速度方向相反
C.2~4 s内,甲、乙均做减速运动
D.6 s末,甲、乙两物体均回到原出发点
BD
方法技巧 v-t图像和x-t图像的应用技巧
(1)确认是哪种图像,究竟是v-t图像还是x-t图像。
(2)理解并熟记五个对应关系
①斜率与加速度或速度对应;
②纵截距与初速度或初始位置对应;
③横截距对应速度或位移为零的时刻;
④交点对应速度或位置相同;
⑤拐点对应运动状态发生改变。
例2.ETC是高速公路上电子不停车收费系统的简称。一辆汽车在进入ETC通道入口前减速到以54 km/h的速度匀速行驶,在进入ETC通道入口时速度减为18 km/h,匀速到达自动栏杆处,在通道内,ETC已完成车辆信息识别同时自动栏杆抬起,汽车通过自动栏杆之后,立刻加速到原来的速度,这一过程中其v-t图像如图所示,则( )
知识点二 非常规图像及应用
1.a-t图像中的五点信息
线 截距 交点 斜率 面积
(1)倾斜直线表示变加速直线运动; (2)平行于横轴的直线表示匀变速直线运动 纵截距表示t=0时的加速度 表示两物体该时刻加速度相同 过某点直线(或切线)的斜率表示加速度变化的快慢 表示物体的速度变化量
2.利用a-t图像求末速度:已知某段时间的初速度v0,求出a-t图像与坐标轴所围面积Δv,则这段时间的末速度v=v0+Δv。
3.v2-x图像中的四点信息
线 截距 交点 斜率
倾斜直线表 示匀变速直 线运动 纵截距表示初速度的二次方 表示两物体该时刻速度的二次方相等 表示加速度的2倍
【例3】 (多选)无人驾驶汽车作为汽车的前沿科技,目前尚在完善中,它车头装有一个激光雷达,就像车辆的“鼻子”,随时“嗅”着前方88 m范围内车辆和行人的“气息”,制动反应时间为0.2 s,比有人驾驶汽车平均快1 s。如图所示为在某次测试场地进行制动测试时获得的一部分图像(v为汽车的速度,x为位置坐标)。关于该无人驾驶汽车在该路段的制动测试,下列说法正确的是( )
A.制动加速度大小为10 m/s2
B.以30 m/s的速度匀速行驶时,从“嗅”到前方行人
“气息”到停止需要3 s
C.以30 m/s的速度匀速行驶时,从“嗅”到前方行人
“气息”到停止的距离为51 m
D.最大安全速度是40 m/s
ACD
例4.(2023山东济南高一期末)如图所示,小勤用手机传感器记录了一段时间内某汽车加速度随时间变化的图像。设汽车前进的方向为正方向,已知小勤计时的零时刻汽车仪表盘显示车速为72 km/h。根据所学知识分析,以下说法正确的是( )
A.第5 s末汽车的速度约为12 m/s
B.第7 s末汽车速度为负,此时该汽车可能正在倒车
C.第7 s末汽车的速度约为16 m/s
D.汽车在2~5 s内位移小于5~7 s内位移
C
2
5
7
16
20
32
知识点三 追及和相遇问题
1.对“相遇”“追及”的认识
(1)相遇问题
两个物体(均可看成质点)在同一直线上运动,当它们同时到达同一位置时,即相遇。
①如图所示,若两个物体相向运动,则二者位移大小之和等于开始时两物体间的距离,即xA+xB=x0时相遇。
A
B
②如图所示,若两个物体同向运动,则二者位移大小之差等于开始时两物体间的距离,即xA-xB=x0时相遇。
(2)追及问题
同向运动的物体,若后者能追上前者,则追上时,两者处于同一位置,且后者的速度不小于前者的速度。
B
A
2.追及相遇问题中的一个条件和两个关系
(1)一个条件:即两者速度相等,它往往是物体间能够追上、追不上或两者距离最大、最小的临界条件,也是分析判断的切入点。
(2)两个关系:即两者时间关系和位移关系,这两个关系可通过画两者的运动示意图得到。
对点训练一
3.追及相遇问题常见的情况
假设物体A追物体B,开始时两个物体相距x0,有三种常见情况:
(1)若vA=vB时,xA≥xB+x0,则A追上B;若xA=xB+x0时,vA≥vB,则A追上B。若vA=vB时,xA
(3)若使两物体不相撞,则要求当vA=vB时,xA
4.四种常用方法
物理分 析法 建立两物体运动的情境并画出示意图,找出两物体的位移、速度及时间关系,选择公式列方程求解
函数法 设两物体在t时刻相遇,然后根据位移关系列出关于t的方程f(t)=0,若方程f(t)=0无正实数解,则说明这两个物体不可能相遇;若方程f(t)=0存在正实数解,说明这两个物体能相遇
图像法 ①若用x-t图像求解,分别作出两物体的x-t图像,如果两物体的位移—时间图线相交,则说明两物体相遇;②若用v-t图像求解,则注意比较图线与时间轴所围图形的面积
相对运 动法 取其中一个运动物体为参考系,分析另一个物体相对它的运动,当两者的相对位移为零时相遇,计算时需要将速度、位移、加速度都转换为相对速度、相对位移、相对加速度代入公式
5.解题思路流程
对点训练三
【例5】 一辆汽车以3 m/s2的加速度开始启动的瞬间,一辆以6 m/s的速度做匀速直线运动的自行车恰好从汽车的旁边通过,运动方向与汽车相同。试求:
(1)汽车在追上自行车前与自行车相距最远时的运动时间以及此时两者间的距离。
(2)汽车追上自行车所用时间和追上自行车时汽车的瞬时速度。
汽车
自行车
解析 (1)方法一:物理分析法
汽车与自行车的速度相等时两车相距最远,设此时经过的时间为t1,汽车的速度为v1,两车间的距离为Δx,则有v1=at1=v自
汽车与自行车相距的最远距离为
方法二:图像法
自行车和汽车运动的v-t图像如图所示,由图可以看出,在相遇前,t1时刻两车速度相等,两车相距最远,此时的距离为阴影三角形的面积,
方法三:函数法
设汽车在追上自行车之前经过时间t1两车相距最远,则
由二次函数求极值的条件知t1=2 s时,Δx最大
所以Δx=6 m。
(2)方法一:当两车位移相等时,汽车追上自行车,设此时经过的时间为t2,汽车的瞬时速度为v2,则有
v2=at2=3×4 m/s=12 m/s。
方法二:由图可以看出,在t1时刻之后,由图线v自、v汽和t=t2构成的三角形的面积与标有阴影的三角形面积相等,此时汽车与自行车的位移相等,即汽车与自行车相遇。由几何关系知t2=2t1=4 s
v2=at2=3×4 m/s=12 m/s。
方法技巧 追及问题常用的临界条件
(1)速度小者(但加速度大)追速度大者(但加速度小),追上前两个物体速度相等时,有最大距离。
(2)速度大者追速度小者,若不能追上,则两个物体速度相等时,有最小距离。即必须在此之前追上,否则就追不上。
例6.图a为马拉松比赛中两位参赛选手的某一情形,甲、乙两人起跑时都做匀加速直线运动,达到某一速度后都各自做匀速直线运动直至终点,他们的速度—时间图像如图b所示,则下列说法正确的是( )
A.乙选手起跑2 s后刚好追上甲选手
B.乙选手起跑时,甲选手正好跑了3 m
C.相遇前甲、乙两选手之间的最大距离为4 m
D.乙选手超过甲选手后,两选手可能再次相遇
C
1.(用图像分析追击相遇问题)(2023广东广州高一期末)某兴趣小组举行机器人跑步比赛,甲、乙两机器人均做直线运动。两机器人运动的位移—时间图像如图所示,其中机器人乙的x-t图线是关于x轴对称的抛物线的一部分,则下列说法正确的是( )
A.机器人甲先做匀减速直线运动后做匀速直线运动
B.机器人甲在0~10 s内的平均速度为-1.5 m/s
C.机器人乙一定做初速度为零的匀加速直线运动
D.在0~10 s内甲、乙机器人相遇两次,且相遇时速度可能相等
C
2.(追及相遇问题)甲车以3 m/s2的加速度由静止开始做匀加速直线运动,乙车落后2 s在同一地点由静止出发,以4 m/s2的加速度做匀加速直线运动,两车速度方向一致。在乙车追上甲车之前,两车距离的最大值是( )
A.18 m B.24 m C.22 m D.28 m
B
3.(v-t图像的应用)物体a、b从同一位置沿同一直线运动的v-t图像如图所示,下列说法正确的是( )
A.t=2 s时,a、b的速度方向均发生改变
B.t=4 s时,a、b相距20 m
C.前4 s,a、b均做匀变速直线运动
D.前4 s,a与b的加速度始终相同
B
4.(a-t图像的应用)(2023安徽阜阳高一月考)某同学正用遥控器控制一架无人机运送物体,t=0时物体的速度向上,且为1 m/s,取竖直向上为正方向,无人机的加速度随时间变化的关系图像如图所示,则下列说法正确的是( )
A.在0~1 s内物体做匀加速直线运动
B.物体在1 s末的速度为3 m/s
C.1 s末物体开始向下运动
D.0~3 s内,3 s末物体离地面最远
D
