人教版数学六年级上册第五单元测试(含解析)
文档属性
| 名称 | 人教版数学六年级上册第五单元测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 470.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 00:00:00 | ||
图片预览




文档简介
人教版数学六年级上册第五单元测试
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
一、选择题
1.一个直径为6cm的半圆,面积是( )cm2。
A.14.13 B.28.26 C.37.68 D.15.42
2.墨子说:“圆,一中同长也。”“一中”指( )。
A.圆心 B.半径 C.直径 D.周长
3.一个圆的半径变为原来的4倍,则这个圆的面积变为原来的( )。
A.2倍 B.4倍 C.8倍 D.16倍
4.一个圆的直径等于一个正方形的边长,这个圆的面积( )正方形的面积。
A.大于 B.小于 C.等于 D.无法比较
5.在用两根同样长的铁丝分别围成正方形和圆,比较它们的面积,结果是( )。
A.正方形的面积比较大 B.圆的面积比较大
C.面积相同 D.不能确定
二、填空题
6.如图所示,点O是( ),线段OC是( ),线段( )是直径。
7.一个零件的半径是0.5cm,它的周长是( )。
8.圆的半径扩大到原来的3倍,它的面积就扩大到原来的( )倍。
9.数学课上,王老师要求同学们用圆规画一个圆。敏敏画的圆的周长是15.7cm,这个圆的半径是( )cm。
10.每个半圆的半径是( )dm,每个半圆的面积是( )dm2。
11.一个时钟的分针长4厘米,当它正好走一圈时,它的尖端走了( )厘米,分针所扫过的面积是( )平方厘米。
12.小玲从一张长30cm、宽20cm的彩纸上剪下一个最大的圆,这个圆的半径是( )cm,周长是( )cm,面积是( )cm2。
13.为了美化校园环境,学校准备在周长是37.68m的圆形花坛外铺一条2m宽的环形小路,这条小路的面积是( )m2。
14.画一个周长是31.4cm的圆,圆规两脚之间的距离是( )cm,这个圆中最长的线段是( )cm,这个圆的面积是( )。
15.在图中,圆的面积与长方形面积是相等的,长方形的长是18.84厘米,圆的面积为( )平方厘米。
三、判断题
16.半圆的面积就是圆的面积除以2。( )
17.圆周率是圆的周长和圆的半径的比值。( )
18.一个周长是12.56dm的圆平均分成两个半圆,每个半圆的周长是6.28dm。( )
19.如下图,一个正方形被圆成了甲、乙两部分,这两部分的周长相等。( )
20.在一个长12厘米、宽9厘米的长方形里画一个最大的圆,这个圆的直径是9厘米。( )
四、计算题
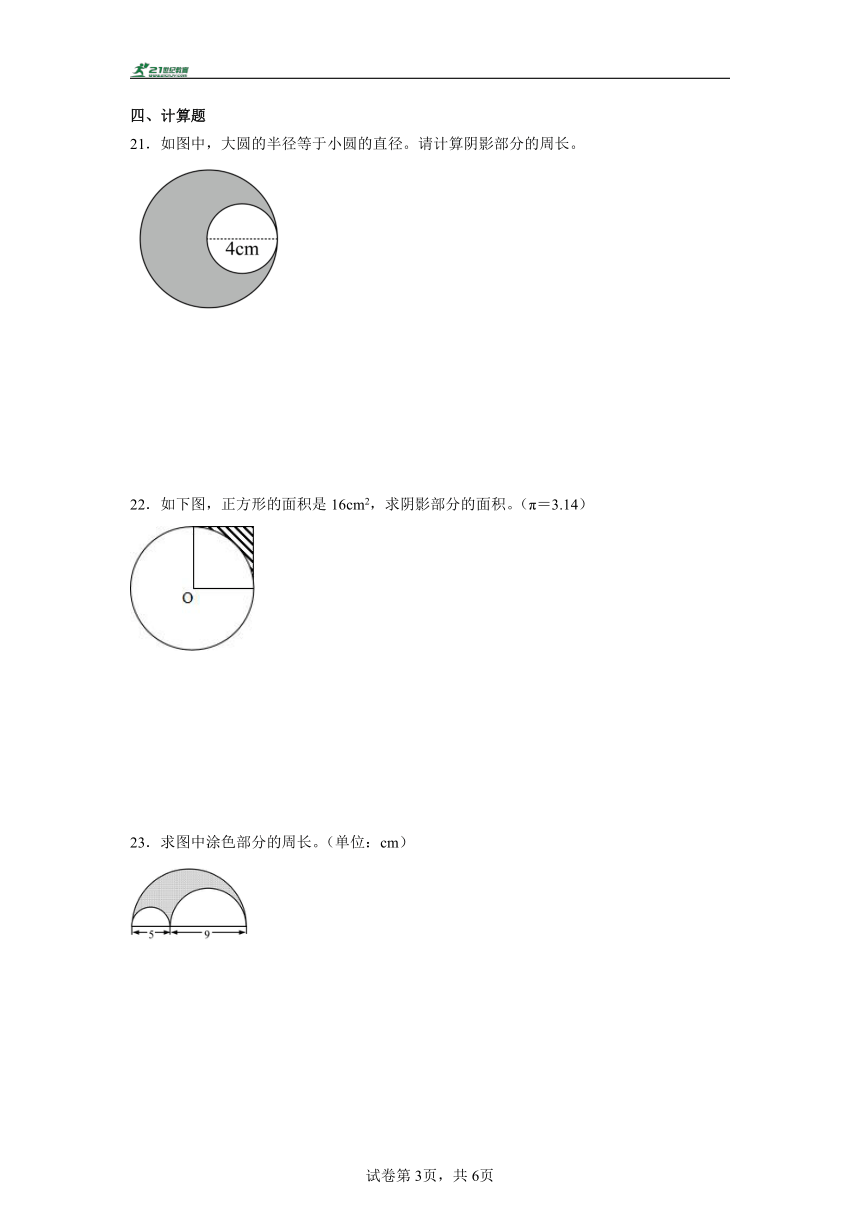
21.如图中,大圆的半径等于小圆的直径。请计算阴影部分的周长。
22.如下图,正方形的面积是16cm2,求阴影部分的面积。(π=3.14)
23.求图中涂色部分的周长。(单位:cm)
五、解答题
24.有一圆形蓄水池。它的周长约是125.6米,它的占地面积约是多少平方米?
25.滨江公园有一个圆形花坛(如图),半径是6米,如果要在花坛周围加宽1米。加宽后花坛的面积是多少平方米?
26.目前世界上能骑行的双轮自行车车轮直径最大的为3.05米,车轮转动一周可行多少米?
27.王师傅用10米长的绳子绕礼堂大厅的柱子3周后还余0.58米,大厅柱子的直径是多少米?
28.黄柏山景区有一棵千年古树。聪聪测量出这棵树的树干一周长5.652m。树干的横截面近似于圆,这棵古树横截面的面积是多少?
29.如图,学校操场的跑道是由一个长方形的两条长边和两个半圆组成的,跑道一周的长度是多少?
30.将一个圆平均分成若干等份后,拼成一个宽等于半径的近似长方形。这个长方形的周长比圆的周长多6厘米。求原来圆的周长和面积。
31.某俱乐部有一个圆形舞池,周长为37.68米,现准备把半径加长1米,舞池面积可增加多少平方米?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 A A D B B
1.A
【分析】根据圆的面积公式S=πr2,求出圆的面积,再除以2,即是半圆的面积。
【详解】3.14×(6÷2)2÷2
=3.14×32÷2
=3.14×9÷2
=28.26÷2
=14.13(cm2)
这个半圆的面积是14.13cm2。
故答案为:A
2.A
【分析】圆有一个圆心,半径和直径都相等。
【详解】根据分析可知, “圆,一中同长也。”的“一中”指的是一个圆心。
故答案为:A
【点睛】此题主要考查学生对圆特征的理解与认识,把握概念关键点即可。
3.D
【分析】根据圆的面积公式S=πr2,以及积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几;可知:一个圆的半径变为原来的4倍,则这个圆的面积变为原来的42倍,据此解答。
【详解】42=4×4=16
一个圆的半径变为原来的4倍,则这个圆的面积变为原来的16倍。
故答案为:D
【点睛】本题考查圆的面积公式以及积的变化规律的应用。明确一个圆的半径变为原来的n倍,则这个圆的面积变为原来的n2倍。
4.B
【分析】根据题意,可设正方形的边长为4厘米,那么圆的半径为2厘米,可根据正方形的面积公式和圆的面积公式进行计算后再比较即可得到答案。
【详解】设正方形的边长为4厘米,则圆的半径为2厘米,
正方形的面积为:4×4=16(平方厘米),
圆的面积为:3.14×22=12.56(平方厘米),
所以正方形的面积大于圆的面积,即这个圆的面积小于正方形的面积。
故答案为:B
【点睛】此题主要考查的是正方形的面积公式和圆的面积公式的应用。
5.B
【分析】假设两根同样长的铁丝的长度都是62.8厘米,根据圆的周长公式:C=2πr,正方形的周长公式:C=4a,分别求出半径和正方形的边长,再根据圆的面积公式:S=πr2,正方形的面积公式:S=a2,求出它们的面积,进行比较即可。
【详解】假设周长都是62.8厘米,正方形的面积是:
(62.8÷4)×(62.8÷4)
=15.7×15.7
=246.49(平方厘米)
圆的面积是:
3.14×(62.8÷3.14÷2)2
=3.14×102
=3.14×100
=314(平方厘米)
246.49<314
所以圆的面积大。
故答案为:B
【点睛】此题主要考查周长相等的圆和正方形的面积大小的比较,可以通过举例来证明,更主要的是通过平时知识的积累,发现规律,按照所发现的规律进行解答。
6. 圆心 半径 AB/BA
【分析】圆心的位置决定了圆的位置,半径决定圆的大小。
连接圆心和圆上任意一点的线段叫做半径;通过圆心并且两端都在圆上的线段都叫做直径。
【详解】如图所示,点O是圆心,线段OC是半径,线段AB是直径。
7.3.14cm/3.14厘米
【分析】已知零件的半径是0.5cm,根据圆的周长公式C=2πr,代入数据计算,即可求出这个零件的周长。
【详解】2×3.14×0.5=3.14(cm)
它的周长是3.14cm。
8.9
【分析】圆的面积公式是S=πr2。半径扩大3倍后,变成了3r,则面积变成了π(3r)2=9πr2。据此解答。
【详解】设圆的半径为r,扩大前的面积为:πr2,扩大后的面积为:9πr2,
9πr2÷(πr2)=9,圆的半径扩大到原来的3倍,它的面积就扩大到原来的9倍。
【点睛】本题主要考查圆的面积公式的灵活运用。
9.2.5
【分析】根据圆的半径=周长÷圆周率÷2,列式计算即可。
【详解】15.7÷3.14÷2=2.5(cm)
这个圆的半径是2.5cm。
10. 4 25.12
【分析】观察图形可知,圆的直径相当于正方形的边长,再根据半径=直径÷2,据此可求出每个半圆的半径;根据圆的面积公式:S=πr2,据此求出整圆的面积,再除以2即可求出每个半圆的面积。
【详解】8÷2=4(dm)
3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(dm2)
则每个半圆的半径是4dm,每个半圆的面积是25.12dm2。
11. 25.12 50.24
【分析】分针尖端走过的路程是以分针长为半径的圆的周长,分针所扫过的面积是以分针长为半径的圆的面积,据此解答。
【详解】(1)2×3.14×4
=6.28×4
=25.12(厘米)
(2)3.14×42
=3.14×16
=50.24(平方厘米)
【点睛】掌握圆周长和面积的计算公式是解答题目的关键。
12. 10 62.8 314
【分析】以长方形的宽为直径的圆是彩纸上最大的圆,在同一个圆中,半径是直径一半,最后利用“”和“”求出圆的周长和面积,据此解答。
【详解】半径:20÷2=10(cm)
周长:3.14×20=62.8(cm)
面积:3.14×102=314(cm2)
【点睛】找出最大圆的直径并熟记圆的周长和面积计算公式是解答题目的关键。
13.87.92
【分析】在周长是37.68米的花坛(如图)外围铺一条2米宽的环形小路,这条小路就是一个圆环,已知内圆的周长是37.68米,根据圆的周长公式,求出半径r,外圆的半径就是r+2米,圆环的面积即可求出,依此计算填空即可。
【详解】内圆半径:37.68÷2÷3.14
=18.84÷3.14
=6(m)
外圆半径:6+2=8(m)
面积:3.14×(82-62)
=3.14×28
=87.92(m2)
【点睛】此题考查了有关圆的应用题,理清思路,灵活应用圆的周长公式和面积公式是解决此题的关键。
14. 5 10 78.5
【分析】在画圆时,圆规两脚间的距离是半径,逆用圆的周长公式可得:半径=圆的周长÷圆周率÷2;这个圆中最长的线段即直径,直径=半径×2,再根据圆的面积=πr2,代入数据解答即可。
【详解】31.4÷3.14÷2
=10÷2
=5(cm)
5×2=10(cm)
3.14×52
=3.14×25
=78.5(cm2)
画一个周长是31.4cm的圆,圆规两脚之间的距离是5cm,这个圆中最长的线段是10cm,这个圆的面积是78.5。
15.113.04
【分析】观察可知,圆的半径=长方形的宽,设圆的半径为r厘米,根据圆的面积=πr2=长方形的面积=长×宽,列出方程求出r的值,再根据圆的面积公式求出圆的面积即可。
【详解】解:设圆的半径为r厘米。
3.14×r2=r×18.84
3.14×r2÷r=r×18.84÷r
3.14r=18.84
3.14r÷3.14=18.84÷3.14
r=6
3.14×62
=3.14×36
=113.04(平方厘米)。
圆的面积为113.04平方厘米。
【点睛】关键是掌握并灵活运用长方形和圆的面积公式,用方程解决问题的关键是找到等量关系。
16.√
【分析】围成圆的平面的大小叫做圆的面积;半圆的面积即是圆面积的一半。
【详解】如图:
半圆的面积就是圆的面积除以2。
原题说法正确。
故答案为:√
【点睛】理解圆的面积的意义是解题的关键。
17.×
【分析】圆周率是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学中普遍存在的数学常数。
【详解】圆周率是圆的周长和圆的直径的比值,所以原题说法错误。
【点睛】关键是理解圆周率的意义,圆的周长=πd。
18.×
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径的长度,根据半圆的周长公式:C=πd÷2+d,把数据代入公式求出每个半圆的周长,然后与6.28dm进行比较,据此判断。
【详解】12.56÷2+12.56÷3.14
=6.28+4
=10.28(dm)
所以每个半圆的周长是10.28dm。
故答案为:×
【点睛】此题考查的目的是理解半圆周长的意义,掌握半圆的周长公式及应用。
19.√
【分析】由图可知,甲、乙两部分的周长都是两条正方形的边长和一条圆弧的长度之和,据此解答。
【详解】由分析可得:甲、乙的周长都是由两条正方形的边长和一条圆弧的长度之和组成,因此相等,原题说法正确。
故答案为:√
【点睛】解决此题的关键是明白圆弧部分是二者公共边长,从而轻松解决。
20.√
【分析】在这个长方形里画的最大圆的直径应等于长方形的宽,长方形的宽是9厘米,据此判断即可。
【详解】如图:
在一个长12厘米、宽9厘米的长方形里画一个最大的圆,这个圆的直径是9厘米。说法正确。
故答案为:√
21.37.68cm
【分析】观察图形可知,阴影部分的周长=大圆的周长+小圆的周长,再根据圆的周长公式:C=πd或C=2πr,据此进行计算即可。
【详解】3.14×2×4+3.14×4
=6.28×4+3.14×4
=25.12+12.56
=37.68(cm)
则阴影部分的周长为37.68cm。
22.
【分析】假设正方形的边长为,根据正方形的面积可知,cm2,可求出边长的长度,即圆的半径长度,利用圆的面积公式,求出圆的面积,空白部分正好占,所以阴影部分的面积等于正方形的面积减去个圆的面积即可。
【详解】,求出,即
23.43.96cm
【分析】观察图形可知,涂色部分的周长=直径为(5+9)cm圆周长的一半+直径为9cm圆周长的一半+直径为5cm圆周长的一半,根据圆的周长公式C=πd,代入数据计算求解。
【详解】3.14×(5+9)÷2+3.14×9÷2+3.14×5÷2
=3.14×14÷2+3.14×9÷2+3.14×5÷2
=21.98+14.13+7.85
=43.96(cm)
涂色部分的周长是43.96cm。
24.1256平方米
【分析】根据题意可知,求占地面积也就是求这个圆形水池的面积,先根据圆的周长公式,求出圆的半径,再根据圆的面积公式S=πr2,列式解答。
【详解】3.14×(125.6÷3.14÷2)2
=3.14×(40÷2)2
=3.14×202
=3.14×400
=1256(平方米)
答:它的占地面积约是1256平方米。
【点睛】此题主要考查圆的周长公式和圆的面积公式应用。
25.40.82平方米
【分析】圆形花坛的半径是6米,可看作内圆的半径r为6米,环宽是1米,用内圆的半径加环宽,求出外圆的半径R,根据圆环的面积公式:S=,代入数据即可求出加宽后花坛的面积是多少平方米。
【详解】
=
=
=
=40.82(平方米)
答:加宽后花坛的面积是40.82平方米。
【点睛】此题的解题关键是灵活运用圆环的面积公式解决问题。
26.9.577米
【分析】根据题意,可知就是求圆的周长,根据“ C=πd”解答即可。
【详解】3.14×3.05=9.577(米);
答:车轮转动一周可行9.577米。
【点睛】熟练掌握圆的周长公式是解答本题的关键。
27.1米
【分析】根据题意,用10减去0.58可以求出绕柱子3周的长度,再除以3,即可求出绕柱子一周的长度,即柱子的周长。圆的周长=πd,据此用柱子的周长除以π,即可求出它的直径。
【详解】(10-0.58)÷3
=9.42÷3
=3.14(米)
3.14÷3.14=1(米)
答:大厅柱子的直径是1米。
28.2.5434平方米
【分析】根据“r=c÷π÷2”求出圆的半径,再根据“s=πr ”求出圆的面积即可。
【详解】
=0.81×3.14
=2.5434(平方米);
答:这棵古树横截面的面积是2.5434平方米。
【点睛】熟练掌握圆的周长和面积公式并能灵活利用是解答本题的关键。
29.245.6米
【分析】跑道一周的长度=长方形的长×2+圆的周长,据此解答。
【详解】60×2+3.14×40
=120+125.6
=245.6(米)
答:跑道一周的长度是245.6米。
【点睛】灵活运用圆的周长计算公式是解答题目的关键。
30.18.84厘米;28.26平方厘米
【分析】将圆拼成一个近似长方形,周长增加的2条半径,据此可知,2条半径的长度为6厘米,进而求出圆的半径为3厘米,再求出圆的周长和面积即可。
【详解】6÷2=3(厘米);
2×3.14×3
=6.28×3
=18.84(厘米);
3.14×3 =28.26(平方厘米);
答:圆的周长是18.84厘米,面积是28.26平方厘米。
【点睛】明确将圆拼成一个近似长方形,周长增加的2条半径是解答本题的关键,进而求出半径的长度,再进一步解答。
31.40.82平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出这个圆形舞池的半径;求增加的面积,就是求圆环的面积;根据圆环的面积公式:面积=π×(大圆的半径2-小圆的半径2),代入数据,即可解答。
【详解】37.68÷3.14÷2
=12÷2
=6(米)
3.14×[(6+1)2-62]
=3.14×[72-36]
=3.14×[49-36]
=3.14×13
=40.82(平方米)
答:舞池面积可增加40.82平方米。
答案第11页,共22页
答案第11页,共22页
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
一、选择题
1.一个直径为6cm的半圆,面积是( )cm2。
A.14.13 B.28.26 C.37.68 D.15.42
2.墨子说:“圆,一中同长也。”“一中”指( )。
A.圆心 B.半径 C.直径 D.周长
3.一个圆的半径变为原来的4倍,则这个圆的面积变为原来的( )。
A.2倍 B.4倍 C.8倍 D.16倍
4.一个圆的直径等于一个正方形的边长,这个圆的面积( )正方形的面积。
A.大于 B.小于 C.等于 D.无法比较
5.在用两根同样长的铁丝分别围成正方形和圆,比较它们的面积,结果是( )。
A.正方形的面积比较大 B.圆的面积比较大
C.面积相同 D.不能确定
二、填空题
6.如图所示,点O是( ),线段OC是( ),线段( )是直径。
7.一个零件的半径是0.5cm,它的周长是( )。
8.圆的半径扩大到原来的3倍,它的面积就扩大到原来的( )倍。
9.数学课上,王老师要求同学们用圆规画一个圆。敏敏画的圆的周长是15.7cm,这个圆的半径是( )cm。
10.每个半圆的半径是( )dm,每个半圆的面积是( )dm2。
11.一个时钟的分针长4厘米,当它正好走一圈时,它的尖端走了( )厘米,分针所扫过的面积是( )平方厘米。
12.小玲从一张长30cm、宽20cm的彩纸上剪下一个最大的圆,这个圆的半径是( )cm,周长是( )cm,面积是( )cm2。
13.为了美化校园环境,学校准备在周长是37.68m的圆形花坛外铺一条2m宽的环形小路,这条小路的面积是( )m2。
14.画一个周长是31.4cm的圆,圆规两脚之间的距离是( )cm,这个圆中最长的线段是( )cm,这个圆的面积是( )。
15.在图中,圆的面积与长方形面积是相等的,长方形的长是18.84厘米,圆的面积为( )平方厘米。
三、判断题
16.半圆的面积就是圆的面积除以2。( )
17.圆周率是圆的周长和圆的半径的比值。( )
18.一个周长是12.56dm的圆平均分成两个半圆,每个半圆的周长是6.28dm。( )
19.如下图,一个正方形被圆成了甲、乙两部分,这两部分的周长相等。( )
20.在一个长12厘米、宽9厘米的长方形里画一个最大的圆,这个圆的直径是9厘米。( )
四、计算题
21.如图中,大圆的半径等于小圆的直径。请计算阴影部分的周长。
22.如下图,正方形的面积是16cm2,求阴影部分的面积。(π=3.14)
23.求图中涂色部分的周长。(单位:cm)
五、解答题
24.有一圆形蓄水池。它的周长约是125.6米,它的占地面积约是多少平方米?
25.滨江公园有一个圆形花坛(如图),半径是6米,如果要在花坛周围加宽1米。加宽后花坛的面积是多少平方米?
26.目前世界上能骑行的双轮自行车车轮直径最大的为3.05米,车轮转动一周可行多少米?
27.王师傅用10米长的绳子绕礼堂大厅的柱子3周后还余0.58米,大厅柱子的直径是多少米?
28.黄柏山景区有一棵千年古树。聪聪测量出这棵树的树干一周长5.652m。树干的横截面近似于圆,这棵古树横截面的面积是多少?
29.如图,学校操场的跑道是由一个长方形的两条长边和两个半圆组成的,跑道一周的长度是多少?
30.将一个圆平均分成若干等份后,拼成一个宽等于半径的近似长方形。这个长方形的周长比圆的周长多6厘米。求原来圆的周长和面积。
31.某俱乐部有一个圆形舞池,周长为37.68米,现准备把半径加长1米,舞池面积可增加多少平方米?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 A A D B B
1.A
【分析】根据圆的面积公式S=πr2,求出圆的面积,再除以2,即是半圆的面积。
【详解】3.14×(6÷2)2÷2
=3.14×32÷2
=3.14×9÷2
=28.26÷2
=14.13(cm2)
这个半圆的面积是14.13cm2。
故答案为:A
2.A
【分析】圆有一个圆心,半径和直径都相等。
【详解】根据分析可知, “圆,一中同长也。”的“一中”指的是一个圆心。
故答案为:A
【点睛】此题主要考查学生对圆特征的理解与认识,把握概念关键点即可。
3.D
【分析】根据圆的面积公式S=πr2,以及积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几;可知:一个圆的半径变为原来的4倍,则这个圆的面积变为原来的42倍,据此解答。
【详解】42=4×4=16
一个圆的半径变为原来的4倍,则这个圆的面积变为原来的16倍。
故答案为:D
【点睛】本题考查圆的面积公式以及积的变化规律的应用。明确一个圆的半径变为原来的n倍,则这个圆的面积变为原来的n2倍。
4.B
【分析】根据题意,可设正方形的边长为4厘米,那么圆的半径为2厘米,可根据正方形的面积公式和圆的面积公式进行计算后再比较即可得到答案。
【详解】设正方形的边长为4厘米,则圆的半径为2厘米,
正方形的面积为:4×4=16(平方厘米),
圆的面积为:3.14×22=12.56(平方厘米),
所以正方形的面积大于圆的面积,即这个圆的面积小于正方形的面积。
故答案为:B
【点睛】此题主要考查的是正方形的面积公式和圆的面积公式的应用。
5.B
【分析】假设两根同样长的铁丝的长度都是62.8厘米,根据圆的周长公式:C=2πr,正方形的周长公式:C=4a,分别求出半径和正方形的边长,再根据圆的面积公式:S=πr2,正方形的面积公式:S=a2,求出它们的面积,进行比较即可。
【详解】假设周长都是62.8厘米,正方形的面积是:
(62.8÷4)×(62.8÷4)
=15.7×15.7
=246.49(平方厘米)
圆的面积是:
3.14×(62.8÷3.14÷2)2
=3.14×102
=3.14×100
=314(平方厘米)
246.49<314
所以圆的面积大。
故答案为:B
【点睛】此题主要考查周长相等的圆和正方形的面积大小的比较,可以通过举例来证明,更主要的是通过平时知识的积累,发现规律,按照所发现的规律进行解答。
6. 圆心 半径 AB/BA
【分析】圆心的位置决定了圆的位置,半径决定圆的大小。
连接圆心和圆上任意一点的线段叫做半径;通过圆心并且两端都在圆上的线段都叫做直径。
【详解】如图所示,点O是圆心,线段OC是半径,线段AB是直径。
7.3.14cm/3.14厘米
【分析】已知零件的半径是0.5cm,根据圆的周长公式C=2πr,代入数据计算,即可求出这个零件的周长。
【详解】2×3.14×0.5=3.14(cm)
它的周长是3.14cm。
8.9
【分析】圆的面积公式是S=πr2。半径扩大3倍后,变成了3r,则面积变成了π(3r)2=9πr2。据此解答。
【详解】设圆的半径为r,扩大前的面积为:πr2,扩大后的面积为:9πr2,
9πr2÷(πr2)=9,圆的半径扩大到原来的3倍,它的面积就扩大到原来的9倍。
【点睛】本题主要考查圆的面积公式的灵活运用。
9.2.5
【分析】根据圆的半径=周长÷圆周率÷2,列式计算即可。
【详解】15.7÷3.14÷2=2.5(cm)
这个圆的半径是2.5cm。
10. 4 25.12
【分析】观察图形可知,圆的直径相当于正方形的边长,再根据半径=直径÷2,据此可求出每个半圆的半径;根据圆的面积公式:S=πr2,据此求出整圆的面积,再除以2即可求出每个半圆的面积。
【详解】8÷2=4(dm)
3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(dm2)
则每个半圆的半径是4dm,每个半圆的面积是25.12dm2。
11. 25.12 50.24
【分析】分针尖端走过的路程是以分针长为半径的圆的周长,分针所扫过的面积是以分针长为半径的圆的面积,据此解答。
【详解】(1)2×3.14×4
=6.28×4
=25.12(厘米)
(2)3.14×42
=3.14×16
=50.24(平方厘米)
【点睛】掌握圆周长和面积的计算公式是解答题目的关键。
12. 10 62.8 314
【分析】以长方形的宽为直径的圆是彩纸上最大的圆,在同一个圆中,半径是直径一半,最后利用“”和“”求出圆的周长和面积,据此解答。
【详解】半径:20÷2=10(cm)
周长:3.14×20=62.8(cm)
面积:3.14×102=314(cm2)
【点睛】找出最大圆的直径并熟记圆的周长和面积计算公式是解答题目的关键。
13.87.92
【分析】在周长是37.68米的花坛(如图)外围铺一条2米宽的环形小路,这条小路就是一个圆环,已知内圆的周长是37.68米,根据圆的周长公式,求出半径r,外圆的半径就是r+2米,圆环的面积即可求出,依此计算填空即可。
【详解】内圆半径:37.68÷2÷3.14
=18.84÷3.14
=6(m)
外圆半径:6+2=8(m)
面积:3.14×(82-62)
=3.14×28
=87.92(m2)
【点睛】此题考查了有关圆的应用题,理清思路,灵活应用圆的周长公式和面积公式是解决此题的关键。
14. 5 10 78.5
【分析】在画圆时,圆规两脚间的距离是半径,逆用圆的周长公式可得:半径=圆的周长÷圆周率÷2;这个圆中最长的线段即直径,直径=半径×2,再根据圆的面积=πr2,代入数据解答即可。
【详解】31.4÷3.14÷2
=10÷2
=5(cm)
5×2=10(cm)
3.14×52
=3.14×25
=78.5(cm2)
画一个周长是31.4cm的圆,圆规两脚之间的距离是5cm,这个圆中最长的线段是10cm,这个圆的面积是78.5。
15.113.04
【分析】观察可知,圆的半径=长方形的宽,设圆的半径为r厘米,根据圆的面积=πr2=长方形的面积=长×宽,列出方程求出r的值,再根据圆的面积公式求出圆的面积即可。
【详解】解:设圆的半径为r厘米。
3.14×r2=r×18.84
3.14×r2÷r=r×18.84÷r
3.14r=18.84
3.14r÷3.14=18.84÷3.14
r=6
3.14×62
=3.14×36
=113.04(平方厘米)。
圆的面积为113.04平方厘米。
【点睛】关键是掌握并灵活运用长方形和圆的面积公式,用方程解决问题的关键是找到等量关系。
16.√
【分析】围成圆的平面的大小叫做圆的面积;半圆的面积即是圆面积的一半。
【详解】如图:
半圆的面积就是圆的面积除以2。
原题说法正确。
故答案为:√
【点睛】理解圆的面积的意义是解题的关键。
17.×
【分析】圆周率是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学中普遍存在的数学常数。
【详解】圆周率是圆的周长和圆的直径的比值,所以原题说法错误。
【点睛】关键是理解圆周率的意义,圆的周长=πd。
18.×
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径的长度,根据半圆的周长公式:C=πd÷2+d,把数据代入公式求出每个半圆的周长,然后与6.28dm进行比较,据此判断。
【详解】12.56÷2+12.56÷3.14
=6.28+4
=10.28(dm)
所以每个半圆的周长是10.28dm。
故答案为:×
【点睛】此题考查的目的是理解半圆周长的意义,掌握半圆的周长公式及应用。
19.√
【分析】由图可知,甲、乙两部分的周长都是两条正方形的边长和一条圆弧的长度之和,据此解答。
【详解】由分析可得:甲、乙的周长都是由两条正方形的边长和一条圆弧的长度之和组成,因此相等,原题说法正确。
故答案为:√
【点睛】解决此题的关键是明白圆弧部分是二者公共边长,从而轻松解决。
20.√
【分析】在这个长方形里画的最大圆的直径应等于长方形的宽,长方形的宽是9厘米,据此判断即可。
【详解】如图:
在一个长12厘米、宽9厘米的长方形里画一个最大的圆,这个圆的直径是9厘米。说法正确。
故答案为:√
21.37.68cm
【分析】观察图形可知,阴影部分的周长=大圆的周长+小圆的周长,再根据圆的周长公式:C=πd或C=2πr,据此进行计算即可。
【详解】3.14×2×4+3.14×4
=6.28×4+3.14×4
=25.12+12.56
=37.68(cm)
则阴影部分的周长为37.68cm。
22.
【分析】假设正方形的边长为,根据正方形的面积可知,cm2,可求出边长的长度,即圆的半径长度,利用圆的面积公式,求出圆的面积,空白部分正好占,所以阴影部分的面积等于正方形的面积减去个圆的面积即可。
【详解】,求出,即
23.43.96cm
【分析】观察图形可知,涂色部分的周长=直径为(5+9)cm圆周长的一半+直径为9cm圆周长的一半+直径为5cm圆周长的一半,根据圆的周长公式C=πd,代入数据计算求解。
【详解】3.14×(5+9)÷2+3.14×9÷2+3.14×5÷2
=3.14×14÷2+3.14×9÷2+3.14×5÷2
=21.98+14.13+7.85
=43.96(cm)
涂色部分的周长是43.96cm。
24.1256平方米
【分析】根据题意可知,求占地面积也就是求这个圆形水池的面积,先根据圆的周长公式,求出圆的半径,再根据圆的面积公式S=πr2,列式解答。
【详解】3.14×(125.6÷3.14÷2)2
=3.14×(40÷2)2
=3.14×202
=3.14×400
=1256(平方米)
答:它的占地面积约是1256平方米。
【点睛】此题主要考查圆的周长公式和圆的面积公式应用。
25.40.82平方米
【分析】圆形花坛的半径是6米,可看作内圆的半径r为6米,环宽是1米,用内圆的半径加环宽,求出外圆的半径R,根据圆环的面积公式:S=,代入数据即可求出加宽后花坛的面积是多少平方米。
【详解】
=
=
=
=40.82(平方米)
答:加宽后花坛的面积是40.82平方米。
【点睛】此题的解题关键是灵活运用圆环的面积公式解决问题。
26.9.577米
【分析】根据题意,可知就是求圆的周长,根据“ C=πd”解答即可。
【详解】3.14×3.05=9.577(米);
答:车轮转动一周可行9.577米。
【点睛】熟练掌握圆的周长公式是解答本题的关键。
27.1米
【分析】根据题意,用10减去0.58可以求出绕柱子3周的长度,再除以3,即可求出绕柱子一周的长度,即柱子的周长。圆的周长=πd,据此用柱子的周长除以π,即可求出它的直径。
【详解】(10-0.58)÷3
=9.42÷3
=3.14(米)
3.14÷3.14=1(米)
答:大厅柱子的直径是1米。
28.2.5434平方米
【分析】根据“r=c÷π÷2”求出圆的半径,再根据“s=πr ”求出圆的面积即可。
【详解】
=0.81×3.14
=2.5434(平方米);
答:这棵古树横截面的面积是2.5434平方米。
【点睛】熟练掌握圆的周长和面积公式并能灵活利用是解答本题的关键。
29.245.6米
【分析】跑道一周的长度=长方形的长×2+圆的周长,据此解答。
【详解】60×2+3.14×40
=120+125.6
=245.6(米)
答:跑道一周的长度是245.6米。
【点睛】灵活运用圆的周长计算公式是解答题目的关键。
30.18.84厘米;28.26平方厘米
【分析】将圆拼成一个近似长方形,周长增加的2条半径,据此可知,2条半径的长度为6厘米,进而求出圆的半径为3厘米,再求出圆的周长和面积即可。
【详解】6÷2=3(厘米);
2×3.14×3
=6.28×3
=18.84(厘米);
3.14×3 =28.26(平方厘米);
答:圆的周长是18.84厘米,面积是28.26平方厘米。
【点睛】明确将圆拼成一个近似长方形,周长增加的2条半径是解答本题的关键,进而求出半径的长度,再进一步解答。
31.40.82平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出这个圆形舞池的半径;求增加的面积,就是求圆环的面积;根据圆环的面积公式:面积=π×(大圆的半径2-小圆的半径2),代入数据,即可解答。
【详解】37.68÷3.14÷2
=12÷2
=6(米)
3.14×[(6+1)2-62]
=3.14×[72-36]
=3.14×[49-36]
=3.14×13
=40.82(平方米)
答:舞池面积可增加40.82平方米。
答案第11页,共22页
答案第11页,共22页
