7.3 频率与概率 课件(共19张PPT)2024-2025学年高一数学北师版(2019)必修第一册
文档属性
| 名称 | 7.3 频率与概率 课件(共19张PPT)2024-2025学年高一数学北师版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 676.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 12:01:53 | ||
图片预览






文档简介
(共19张PPT)
7.3 频率与概率
第七章 概率
1.理解频率与概率的区别与联系.
2.会用频率估计概率.
对于任何一位篮球运动员,在一次投篮中,命中与否是一个随机事件但是,我们经常能够听到球迷说某某球员投篮很准,这个“很准”是怎么得来的 是否有一个量化的标准 此外,我们经常能够看到在篮球比赛决定胜负的一投时,往往会将这决定胜负的一投交给“最有把握”的球员.既然能否投中是一个随机事件,那么最后一投交给谁都应该一样,不都是听天由命吗 这里的“最有把握”是怎么得来的呢
问题1:表1、表2分别是同一位篮球运动员在5场比赛和5个赛季的投篮命中率的情况,分析两个表格中该运动员的投篮命中率有何特征 为什么有这样的特征
当投篮次数较少时,波动幅度较大;当投篮次数较多时,波动幅度较小.
表1主要说明了频率的波动性,表2则更多地体现了频率的稳定性.
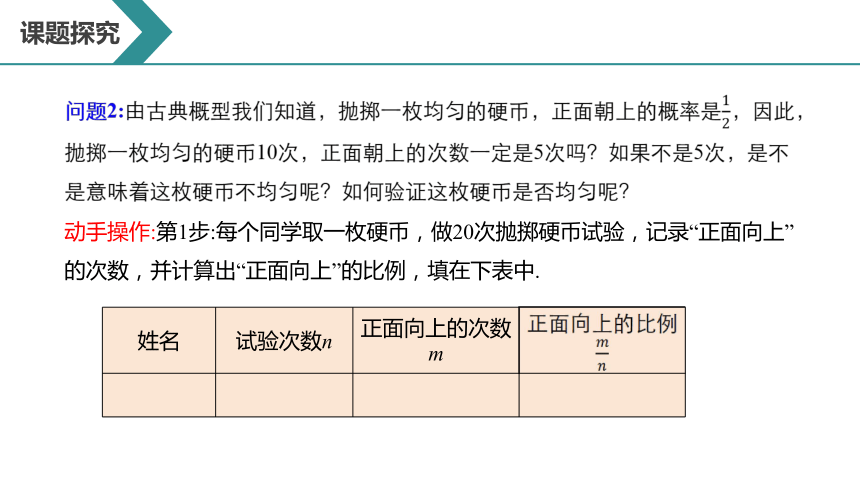
动手操作:第1步:每个同学取一枚硬币,做20次抛掷硬币试验,记录“正面向上”的次数,并计算出“正面向上”的比例,填在下表中.
问题2:由古典概型我们知道,抛掷一枚均匀的硬币,正面朝上的概率是,因此,抛掷一枚均匀的硬币10次,正面朝上的次数一定是5次吗?如果不是5次,是不是意味着这枚硬币不均匀呢?如何验证这枚硬币是否均匀呢?
姓名 试验次数n 正面向上的次数m 正面向上的比例
第2步:由组长把本小组同学的试验结果统计一下,填入下表.
组次 试验次数n 正面向上次数m 正面向上频率
第3步:将全班试验结果收集起来.
班级 试验次数n 正面向上次数m 正面向上频率
试验者 总抛掷次数n 正面朝上的次数m 正面朝上的频率
德·摩根 4092 2048 0.5005
布丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 24000 12012 0.5005
罗曼诺夫斯基 80640 39699 0.4923
材料:历史上曾有很多人做过抛掷硬币试验,其结果如表3(结果精确到0.0001).
表3
抛掷次数逐渐增大,正面朝上的频率稳定在0.5左右
思考1:随着试验次数的不断增加,投篮命中率、硬币正面朝上频率变化有何共同特征
频率通常会在某个常数附近摆动
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.
这个常数叫作随机事件A的概率,记作P(A)(0≤P(A)≤1).
通常用频率来估计概率.
概念生成
思考2:频率与概率有什么区别和联系?
频率反映了一个随机事件出现的频繁程度,频率是随机的,而概率是一个确定的值,通常用概率来反映随机事件发生的可能性的大小,通过大量的重复试验,事件发生的频率会逐渐趋近于某一个常数(概率),因此有时也用频率来作为随机事件概率的估计值.
例1 某射击运动员为备战奥运会,在相同条件下进行射击训练,结果如表:
射击次数n 10 20 50 100 200 500
击中靶心 次数m 8 19 44 92 178 455
击中靶心 的频率 0.8 0.95 0.88 0.92 0.89 0.91
(1)该射击运动员射击一次,击中靶心的概率大约是多少
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少
0.9
解:(2)击中靶心的次数大约为300×0.9=270.
(3)假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗
(4)假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗
(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定击不中靶心.
(4)由概率的意义知,不一定.
例2 试从概率角度解释下列说法的含义:
(1)掷一枚均匀的正方体骰子得到6点的概率是,是否意味着把它掷6次能得
到1次6点
(2)某种病的治愈率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗 如何理解治愈率是0.3
(3)据报道:某地发生的9级地震是“千年一遇”的大地震.在这里,“千年一遇”是什么意思
解:(1)把一枚均匀的骰子掷6次相当于做6次试验,因为每次试验的结果都是随机的,所以做6次试验的结果也是随机的.
这就是说,每掷一次总是随机地出现一个点数,可以是1点,2点,也可以是其他点数,不一定出现6点.
所以掷一枚骰子得到6点的概率是,并不意味着把它掷6次能得到1次6点.
(2)如果把治疗一个病人作为一次试验,治愈率是0.3,是指随着试验次数的增加,即治疗病人人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没治愈是可能的,对后3个人来说,其结果仍然是随机的,即有可能治愈,也可能没有治愈.
(3)“千年一遇”是指0.001的概率,虽然0.001的概率比较小,但不代表没有可能;但也不能说每1 000年就一定会发生一次9级地震.
1.某市正在全面普及数字电视,某住宅区有2万户住户,从中随机抽取200户,调查是否安装数字电视,调查的结果如下表所示,则估计该住宅区已安装数字电视的户数是( )
C
数字电视 老住户 新住户
已安装 30 50
未安装 65 55
A.5 500 B.5 000 C.8 000 D.9 500
2.在天气预报中,有“降水概率预报”.例如,预报“明天降水概率为85%”,这是指( )
A.明天该地区有85%的地区降水,其他15%地区不降水
B.明天该地区约有85%的时间降水,其他时间不降水
C.气象台的专家中,有85%的人认为会降水,另外15%的专家认为不降水
D.明天该地区降水的可能性为85%
D
3.从某自动包装机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位:g):
492,496,494,495,498,497,501,502,504,496,
497,503,506,508,507,492,496,500,501,499.
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5 g~501.5 g之间的概率约为________.
0.25
根据今天所学,回答下列问题:
(1)频率和概率有何区别和联系 这种关系反映了随机现象的什么特点
(2)本节课所学概率与古典概型中的概率有何区别和联系
7.3 频率与概率
第七章 概率
1.理解频率与概率的区别与联系.
2.会用频率估计概率.
对于任何一位篮球运动员,在一次投篮中,命中与否是一个随机事件但是,我们经常能够听到球迷说某某球员投篮很准,这个“很准”是怎么得来的 是否有一个量化的标准 此外,我们经常能够看到在篮球比赛决定胜负的一投时,往往会将这决定胜负的一投交给“最有把握”的球员.既然能否投中是一个随机事件,那么最后一投交给谁都应该一样,不都是听天由命吗 这里的“最有把握”是怎么得来的呢
问题1:表1、表2分别是同一位篮球运动员在5场比赛和5个赛季的投篮命中率的情况,分析两个表格中该运动员的投篮命中率有何特征 为什么有这样的特征
当投篮次数较少时,波动幅度较大;当投篮次数较多时,波动幅度较小.
表1主要说明了频率的波动性,表2则更多地体现了频率的稳定性.
动手操作:第1步:每个同学取一枚硬币,做20次抛掷硬币试验,记录“正面向上”的次数,并计算出“正面向上”的比例,填在下表中.
问题2:由古典概型我们知道,抛掷一枚均匀的硬币,正面朝上的概率是,因此,抛掷一枚均匀的硬币10次,正面朝上的次数一定是5次吗?如果不是5次,是不是意味着这枚硬币不均匀呢?如何验证这枚硬币是否均匀呢?
姓名 试验次数n 正面向上的次数m 正面向上的比例
第2步:由组长把本小组同学的试验结果统计一下,填入下表.
组次 试验次数n 正面向上次数m 正面向上频率
第3步:将全班试验结果收集起来.
班级 试验次数n 正面向上次数m 正面向上频率
试验者 总抛掷次数n 正面朝上的次数m 正面朝上的频率
德·摩根 4092 2048 0.5005
布丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 24000 12012 0.5005
罗曼诺夫斯基 80640 39699 0.4923
材料:历史上曾有很多人做过抛掷硬币试验,其结果如表3(结果精确到0.0001).
表3
抛掷次数逐渐增大,正面朝上的频率稳定在0.5左右
思考1:随着试验次数的不断增加,投篮命中率、硬币正面朝上频率变化有何共同特征
频率通常会在某个常数附近摆动
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.
这个常数叫作随机事件A的概率,记作P(A)(0≤P(A)≤1).
通常用频率来估计概率.
概念生成
思考2:频率与概率有什么区别和联系?
频率反映了一个随机事件出现的频繁程度,频率是随机的,而概率是一个确定的值,通常用概率来反映随机事件发生的可能性的大小,通过大量的重复试验,事件发生的频率会逐渐趋近于某一个常数(概率),因此有时也用频率来作为随机事件概率的估计值.
例1 某射击运动员为备战奥运会,在相同条件下进行射击训练,结果如表:
射击次数n 10 20 50 100 200 500
击中靶心 次数m 8 19 44 92 178 455
击中靶心 的频率 0.8 0.95 0.88 0.92 0.89 0.91
(1)该射击运动员射击一次,击中靶心的概率大约是多少
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少
0.9
解:(2)击中靶心的次数大约为300×0.9=270.
(3)假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗
(4)假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗
(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定击不中靶心.
(4)由概率的意义知,不一定.
例2 试从概率角度解释下列说法的含义:
(1)掷一枚均匀的正方体骰子得到6点的概率是,是否意味着把它掷6次能得
到1次6点
(2)某种病的治愈率是0.3,那么前7个人没有治愈,后3个人一定能治愈吗 如何理解治愈率是0.3
(3)据报道:某地发生的9级地震是“千年一遇”的大地震.在这里,“千年一遇”是什么意思
解:(1)把一枚均匀的骰子掷6次相当于做6次试验,因为每次试验的结果都是随机的,所以做6次试验的结果也是随机的.
这就是说,每掷一次总是随机地出现一个点数,可以是1点,2点,也可以是其他点数,不一定出现6点.
所以掷一枚骰子得到6点的概率是,并不意味着把它掷6次能得到1次6点.
(2)如果把治疗一个病人作为一次试验,治愈率是0.3,是指随着试验次数的增加,即治疗病人人数的增加,大约有30%的人能够治愈,对于一次试验来说,其结果是随机的,因此前7个病人没治愈是可能的,对后3个人来说,其结果仍然是随机的,即有可能治愈,也可能没有治愈.
(3)“千年一遇”是指0.001的概率,虽然0.001的概率比较小,但不代表没有可能;但也不能说每1 000年就一定会发生一次9级地震.
1.某市正在全面普及数字电视,某住宅区有2万户住户,从中随机抽取200户,调查是否安装数字电视,调查的结果如下表所示,则估计该住宅区已安装数字电视的户数是( )
C
数字电视 老住户 新住户
已安装 30 50
未安装 65 55
A.5 500 B.5 000 C.8 000 D.9 500
2.在天气预报中,有“降水概率预报”.例如,预报“明天降水概率为85%”,这是指( )
A.明天该地区有85%的地区降水,其他15%地区不降水
B.明天该地区约有85%的时间降水,其他时间不降水
C.气象台的专家中,有85%的人认为会降水,另外15%的专家认为不降水
D.明天该地区降水的可能性为85%
D
3.从某自动包装机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位:g):
492,496,494,495,498,497,501,502,504,496,
497,503,506,508,507,492,496,500,501,499.
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5 g~501.5 g之间的概率约为________.
0.25
根据今天所学,回答下列问题:
(1)频率和概率有何区别和联系 这种关系反映了随机现象的什么特点
(2)本节课所学概率与古典概型中的概率有何区别和联系
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
