期中复习(一-三章)(含答案) 2024-2025学年浙教版数学七上
文档属性
| 名称 | 期中复习(一-三章)(含答案) 2024-2025学年浙教版数学七上 |  | |
| 格式 | docx | ||
| 文件大小 | 206.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 11:47:50 | ||
图片预览


文档简介
期中复习(一-三章)七上数学浙教版
一、选择题
1.下列各组数中,互为相反数的是( )
A.2与 B.与2 C.2与 D.2与
2.如图所示的图形为四位同学画的数轴,其中正确的是( )
A. B.
C. D.
3.下列各式正确的是( )
A. B. C. D.
4.某仓库新购进一批优质小麦,包装袋上标有质量为的字样,若从中任意挑出一袋,则它的质量最多为( )
A. B. C. D.
5.数轴上一点A向右移动4个单位长度到达点B,若点B再向左移动2个单位长度到达点C.若点C表示的数是-3,则点A表示的数是( )
A.-3 B.-2 C.-5 D.2
6.若与互为相反数,则的值为( )
A. B. C. D.或
7.实数在数轴上表示的位置如图所示,则以下错误的是( )
A. B. C. D.
8.已知,,则( )
A. B. C.1 D.3
9. 已知min{,x2,x}表示取三个数中最小的那个数,例如:当x=9,min{,x2,x}=min{,92,9}=3.当min{,x2,x}=时,则x的值为( )
A. B. C. D.
10.我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),是逢2进1的计数制,它们两者之间可以互相换算,如将(101)2, (1011)2换算成十进制数应为:
,
按此方式,则(101)2+ (1111)2 =( )
A.(10000)2 B.(10101)2 C.(1011111)2 D.(10100)2
二、填空题
11.写出一个小于的正无理数 .
12.人的眼睛可看见的红光的波长为0.000077厘米(精确到0.00001厘米).将近似数用科学记数法表示为 .
13.绝对值小于或等于1的整数有 .
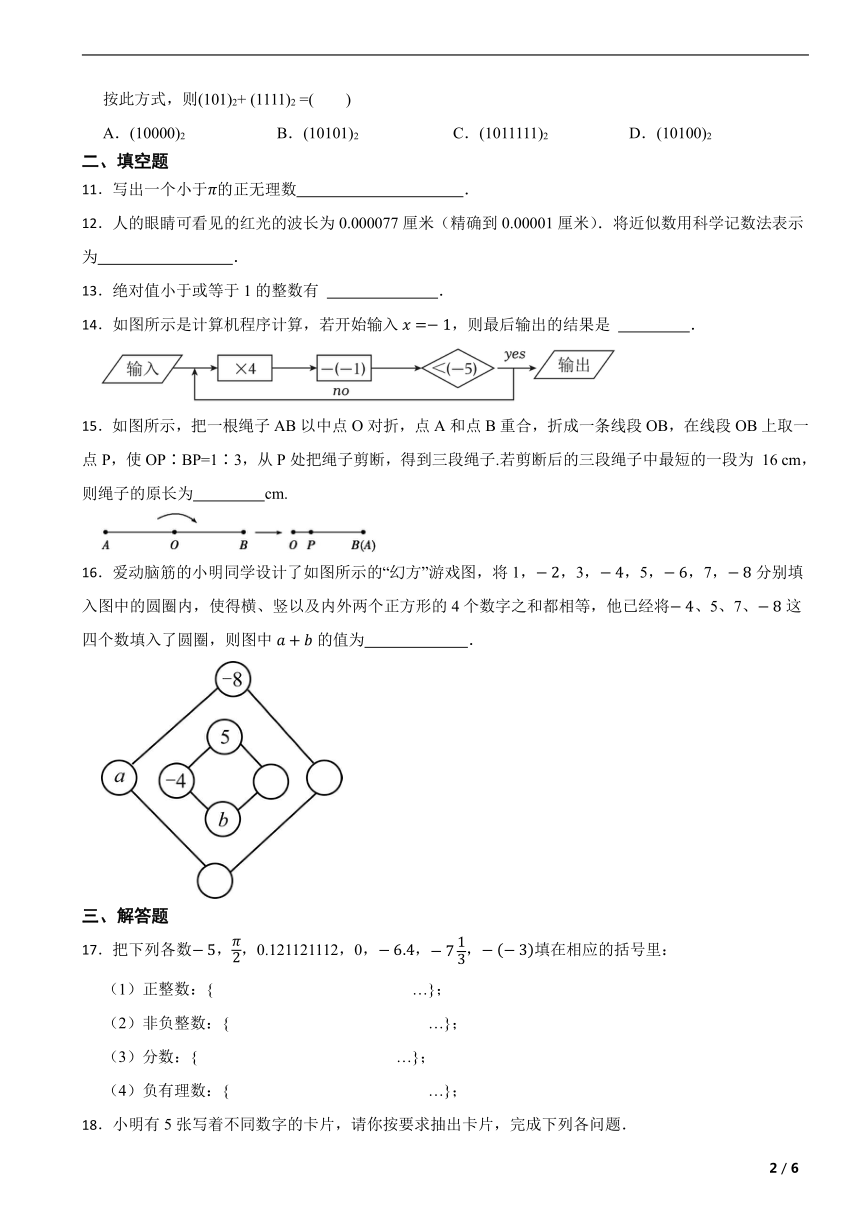
14.如图所示是计算机程序计算,若开始输入,则最后输出的结果是 .
15.如图所示,把一根绳子AB以中点O对折,点A和点B重合,折成一条线段OB,在线段OB上取一点P,使OP∶BP=1∶3,从P处把绳子剪断,得到三段绳子.若剪断后的三段绳子中最短的一段为 16 cm,则绳子的原长为 cm.
16.爱动脑筋的小明同学设计了如图所示的“幻方”游戏图,将1,,3,,5,,7,分别填入图中的圆圈内,使得横、竖以及内外两个正方形的4个数字之和都相等,他已经将、5、7、这四个数填入了圆圈,则图中的值为 .
三、解答题
17.把下列各数,,0.121121112,0,,,填在相应的括号里:
(1)正整数:{ …};
(2)非负整数:{ …};
(3)分数:{ …};
(4)负有理数:{ …};
18.小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题.
(1)从中抽取出2张卡片,使这2张卡片上的数字相减最大,并计算出最大结果;
(2)从中抽取出2张卡片,使这2张卡片上的数字相乘得到的积最大,并计算出最大结果.
19.已知的平方根为它本身,的算术平方根是3,的立方根是2.
(1)求a,b,c的值.
(2)求的平方根.
20. 出租车司机小王某天上午营运全是在东西走向的光明大道上进行的,如果规定向东为正,向西为负,他这天上午行车里程(单位:千米)如下:
(1)将最后一名乘客送到目的地时,小王距上午出车时的出发点多远?
(2)若汽车耗油量为0.12升/千米,这天上午小王共耗油多少升?
21.设表示不超过a的最大整数,例如:.
(1)填空: ; .
(2)令,求.
22.阅读理解:因为,所以,所以的整数部分是1,将这个数减去其整数部分,差就是小数部分.例如:的小数部分为.类似地,因为,所以的小数部分就是.
请根据上述材料,解答下列相关问题.
(1)的整数部分是__________,小数部分是__________.
(2)若的小数部分为a,的整数部分为b,求的值.
23.综合与探究:
【背景知识】在学习绝对值后,我们知道,表示数在数轴上的对应点与原点的距离.如图,如:表示5在数轴上的对应点到原点的距离.而,即也可理解为5、0在数轴上对应的两点之间的距离.类似的,表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如的几何意义是数轴上表示有理数3的点与表示数的点之间的距离,一般地,点、在数轴上分别表示数、,那么、之间的距离可表示为.
【问题解决】请根据绝对值的意义并结合数轴解答下列问题:
(1)数轴上表示2和3的两点之间的距离是__________;数轴上表示和的两点之间的距离是__________;
(2)数轴上点表示的数是2,、两点的距离为3,则点表示的数是__________
(3)的几何意义是数轴上表示有理数__________的点与表示的点之间的距离;
【拓展延伸】
(4)如图,、分别为数轴上的两点,点对应的数为,点对应的数为100.现有一只电子蚂蚁从点出发,以6个单位/秒的速度向左运动,同时另一只电子蚂蚁恰好从点出发,以4个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的点相遇,请你求出点所对应的数是多少.
参考答案
1-5. DDDCC
6-10.ADDCD
11.(答案不唯一)
12.厘米
13.0,1,
14.
15.64
解:设绳子的原长为xcm,
∵点O是AB的中点,
∴OA=OB=xcm,
∵OP:BP=1:3,
∴OP=cm,PB=PA=cm,
∴剪断后的三段绳子分别是xcm,xcm,xcm,
∵最短的一段为 16 cm,
∴x=16,
∴x=64,
∴绳子的原长为64cm.
16.或
解:设小圈上的数为c,大圈上的数为d,
∵,且横、竖以及内外两圈上的4个数字之和都相等,
∴内外两个圈的4个数字之和都是,横、竖的4个数字之和也是,
则,得,
,得,
,,
当时,,,
当时,,,
17.(1)
(2)0,
(3)0.121121112,,
(4),,
18.(1)则抽取5和两张卡片的数字相减最大,最大为12.
(2)抽取和两张卡片的数字相乘得到的积最大,最大为21.
19.(1),,
(2)
20.(1)解:15-2+5-1+10-3-2+12+4-5+6=39(千米)
(2)解:|+15|+|-2|+|+5|+|-1|+|+10|+|-3|+|-2|+|+12|+|+4|+|-5|+|+6|=65(千米),
65×0.12=7.8(升)
21.(1)2,
(2)4
22.(1),
(2)
23.(1)1,;(2)或5;(3);(4)28
1 / 1
一、选择题
1.下列各组数中,互为相反数的是( )
A.2与 B.与2 C.2与 D.2与
2.如图所示的图形为四位同学画的数轴,其中正确的是( )
A. B.
C. D.
3.下列各式正确的是( )
A. B. C. D.
4.某仓库新购进一批优质小麦,包装袋上标有质量为的字样,若从中任意挑出一袋,则它的质量最多为( )
A. B. C. D.
5.数轴上一点A向右移动4个单位长度到达点B,若点B再向左移动2个单位长度到达点C.若点C表示的数是-3,则点A表示的数是( )
A.-3 B.-2 C.-5 D.2
6.若与互为相反数,则的值为( )
A. B. C. D.或
7.实数在数轴上表示的位置如图所示,则以下错误的是( )
A. B. C. D.
8.已知,,则( )
A. B. C.1 D.3
9. 已知min{,x2,x}表示取三个数中最小的那个数,例如:当x=9,min{,x2,x}=min{,92,9}=3.当min{,x2,x}=时,则x的值为( )
A. B. C. D.
10.我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),是逢2进1的计数制,它们两者之间可以互相换算,如将(101)2, (1011)2换算成十进制数应为:
,
按此方式,则(101)2+ (1111)2 =( )
A.(10000)2 B.(10101)2 C.(1011111)2 D.(10100)2
二、填空题
11.写出一个小于的正无理数 .
12.人的眼睛可看见的红光的波长为0.000077厘米(精确到0.00001厘米).将近似数用科学记数法表示为 .
13.绝对值小于或等于1的整数有 .
14.如图所示是计算机程序计算,若开始输入,则最后输出的结果是 .
15.如图所示,把一根绳子AB以中点O对折,点A和点B重合,折成一条线段OB,在线段OB上取一点P,使OP∶BP=1∶3,从P处把绳子剪断,得到三段绳子.若剪断后的三段绳子中最短的一段为 16 cm,则绳子的原长为 cm.
16.爱动脑筋的小明同学设计了如图所示的“幻方”游戏图,将1,,3,,5,,7,分别填入图中的圆圈内,使得横、竖以及内外两个正方形的4个数字之和都相等,他已经将、5、7、这四个数填入了圆圈,则图中的值为 .
三、解答题
17.把下列各数,,0.121121112,0,,,填在相应的括号里:
(1)正整数:{ …};
(2)非负整数:{ …};
(3)分数:{ …};
(4)负有理数:{ …};
18.小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题.
(1)从中抽取出2张卡片,使这2张卡片上的数字相减最大,并计算出最大结果;
(2)从中抽取出2张卡片,使这2张卡片上的数字相乘得到的积最大,并计算出最大结果.
19.已知的平方根为它本身,的算术平方根是3,的立方根是2.
(1)求a,b,c的值.
(2)求的平方根.
20. 出租车司机小王某天上午营运全是在东西走向的光明大道上进行的,如果规定向东为正,向西为负,他这天上午行车里程(单位:千米)如下:
(1)将最后一名乘客送到目的地时,小王距上午出车时的出发点多远?
(2)若汽车耗油量为0.12升/千米,这天上午小王共耗油多少升?
21.设表示不超过a的最大整数,例如:.
(1)填空: ; .
(2)令,求.
22.阅读理解:因为,所以,所以的整数部分是1,将这个数减去其整数部分,差就是小数部分.例如:的小数部分为.类似地,因为,所以的小数部分就是.
请根据上述材料,解答下列相关问题.
(1)的整数部分是__________,小数部分是__________.
(2)若的小数部分为a,的整数部分为b,求的值.
23.综合与探究:
【背景知识】在学习绝对值后,我们知道,表示数在数轴上的对应点与原点的距离.如图,如:表示5在数轴上的对应点到原点的距离.而,即也可理解为5、0在数轴上对应的两点之间的距离.类似的,表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如的几何意义是数轴上表示有理数3的点与表示数的点之间的距离,一般地,点、在数轴上分别表示数、,那么、之间的距离可表示为.
【问题解决】请根据绝对值的意义并结合数轴解答下列问题:
(1)数轴上表示2和3的两点之间的距离是__________;数轴上表示和的两点之间的距离是__________;
(2)数轴上点表示的数是2,、两点的距离为3,则点表示的数是__________
(3)的几何意义是数轴上表示有理数__________的点与表示的点之间的距离;
【拓展延伸】
(4)如图,、分别为数轴上的两点,点对应的数为,点对应的数为100.现有一只电子蚂蚁从点出发,以6个单位/秒的速度向左运动,同时另一只电子蚂蚁恰好从点出发,以4个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的点相遇,请你求出点所对应的数是多少.
参考答案
1-5. DDDCC
6-10.ADDCD
11.(答案不唯一)
12.厘米
13.0,1,
14.
15.64
解:设绳子的原长为xcm,
∵点O是AB的中点,
∴OA=OB=xcm,
∵OP:BP=1:3,
∴OP=cm,PB=PA=cm,
∴剪断后的三段绳子分别是xcm,xcm,xcm,
∵最短的一段为 16 cm,
∴x=16,
∴x=64,
∴绳子的原长为64cm.
16.或
解:设小圈上的数为c,大圈上的数为d,
∵,且横、竖以及内外两圈上的4个数字之和都相等,
∴内外两个圈的4个数字之和都是,横、竖的4个数字之和也是,
则,得,
,得,
,,
当时,,,
当时,,,
17.(1)
(2)0,
(3)0.121121112,,
(4),,
18.(1)则抽取5和两张卡片的数字相减最大,最大为12.
(2)抽取和两张卡片的数字相乘得到的积最大,最大为21.
19.(1),,
(2)
20.(1)解:15-2+5-1+10-3-2+12+4-5+6=39(千米)
(2)解:|+15|+|-2|+|+5|+|-1|+|+10|+|-3|+|-2|+|+12|+|+4|+|-5|+|+6|=65(千米),
65×0.12=7.8(升)
21.(1)2,
(2)4
22.(1),
(2)
23.(1)1,;(2)或5;(3);(4)28
1 / 1
同课章节目录
