24.3正多边形和圆(共两课时)
文档属性
| 名称 | 24.3正多边形和圆(共两课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-25 00:00:00 | ||
图片预览



文档简介
24.3 正多边形和圆(1)
教学目标 知识技能 使学生经历正多边形的形成过程,了解正多边形的有关概念,掌握用等分圆周画圆的内接正多边形的方法.
数学思考 使学生丰富对正多边形的认识,通过设计图案,发展学生的形象思维.
解决问题 使学生会等分圆周,利用等分圆周的方法构造正多边形,并会设计图案,发展学生的实践能力和创新精神.
情感态度 通过等分圆周、构造正多边形等实践活动,使学生在数学学习活动中获得成功的体验,建立自信心.
重点 了解圆与正多边形的关系;掌握用量角器等分圆心角来等分圆,从而得到正多边形和尺规作圆内接正方形和正六边形的方法.
难点 对正n边形中“n”的接受和理解.
正多边形和圆正多边形的概念:等分圆周的方法:
问题与情境 师生行为 设计意图
活动一:复习提问1.什么样的图形叫做正多边形? 展示图片(课本P113页图片),你还能举出一些这样的例子吗?2.正多边形与圆有什么关系呢? (引出课题)活动二:等分圆周问题:为什么等分圆周就能得到正多边形呢? 教师提出问题,学生进行回答:各边相等,各角相等的多边形叫做正多边形.并举出生活中的例子.教师可再展示一些图片让学生欣赏.学生根据教师提出的问题进行思考,回忆圆的有关知识,进而回答教师提出的问题.即等分圆周,就可以得到圆内接正多边形,这个圆叫做这个正多边形的外接圆.教师提出问题后,学生认真思考、交流,充分发表自己的见解,并互相补充.教师在学生归纳的基础上进行补充,并以正五边形为例进行证明. 复习正多边形的概念,为今天的课程做准备. 激发学生的学习兴趣.培养学生的思维品质,将正多边形与圆联系起来.并由此引出今天的课题.
问题与情境 师生行为 设计意图
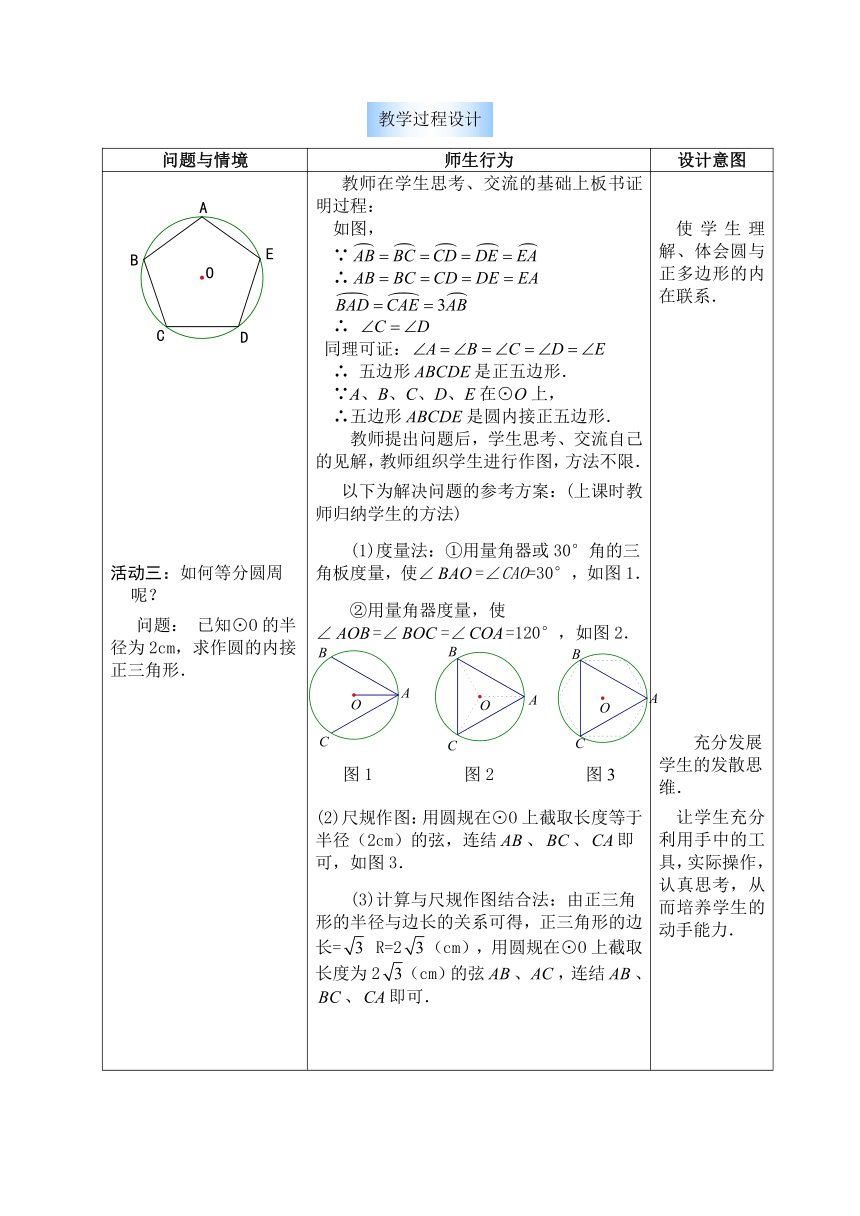
活动三:如何等分圆周呢?问题: 已知⊙O的半径为2cm,求作圆的内接正三角形. 教师在学生思考、交流的基础上板书证明过程:如图, ∵ ∴ ∴ 同理可证:∴ 五边形是正五边形. ∵A、B、C、D、E在⊙O上, ∴五边形ABCDE是圆内接正五边形.教师提出问题后,学生思考、交流自己的见解,教师组织学生进行作图,方法不限. 以下为解决问题的参考方案:(上课时教师归纳学生的方法) (1)度量法:①用量角器或30°角的三角板度量,使∠=∠CAO=30°,如图1.②用量角器度量,使∠=∠=∠=120°,如图2.(2)尺规作图:用圆规在⊙O上截取长度等于半径(2cm)的弦,连结、、即可,如图3. (3)计算与尺规作图结合法:由正三角形的半径与边长的关系可得,正三角形的边长= R=2(cm),用圆规在⊙O上截取长度为2(cm)的弦、,连结、、即可. 使学生理解、体会圆与正多边形的内在联系.充分发展学生的发散思维.让学生充分利用手中的工具,实际操作,认真思考,从而培养学生的动手能力.
问题与情境 师生行为 设计意图
在师生共同作图的基础上,归纳出:正多边形与圆有着密切的联系.如:圆既是轴对称图形,又是中心对称图形,且它的每一条直径所在的直线都是它的对称轴,圆具有旋转不变性.正多边形也是轴对称图形,正n边形有n条对称轴,当n为偶数时,它也是中心对称图形,且绕中心旋转,都能和原来的图形重合.结合图4,给出正多边形的中心、半径、中心角、边心距等概念. 同样说明正多边形与圆有着很多内在的联系.活动四:实际应用参照图5,按照一定比例,画一个停车让行的交通标志的外缘. 在学生作图的基础上,教师归纳出等分圆周的方法: 1.用量角器等分圆: 依据:同圆中相等的圆心角所对应的弧相等. 操作:两种情况:其一是依次画出相等的圆心角来等分圆,这种方法比较准确,但是麻烦;其二是先用量角器画一个圆心角,然后在圆上依次截取等于该圆心角所对弧的等弧,于是得到圆的等分点,这种方法比较方便,但画图的误差积累到最后一个等分点,使画出的正多边形的边长误差较大. 2.用尺规等分圆:(1)作正四边形、正八边形. 教师组织学生,分析、作图.归纳:只要做出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……(2)作正六、三、十二边形. 教师组织学生,分析、作图.归纳:先做出正六边形,则可作正三角形,正十二边形,正二十四边形……理论上我们可以一直画下去,但大家不难发现,随着边数的增加,正多边形越来越接近于圆,正多边形将越来越难画.教师提出问题后,学生认真思考,并在笔记本上试着作图,再与同学进行交流. 教给学生等分圆周的方法,尤其是尺规作正方形、正六边形. 使学生体会随着正多边形边数的增多,正多边形越来越接近圆.
问题与情境 师生行为 设计意图
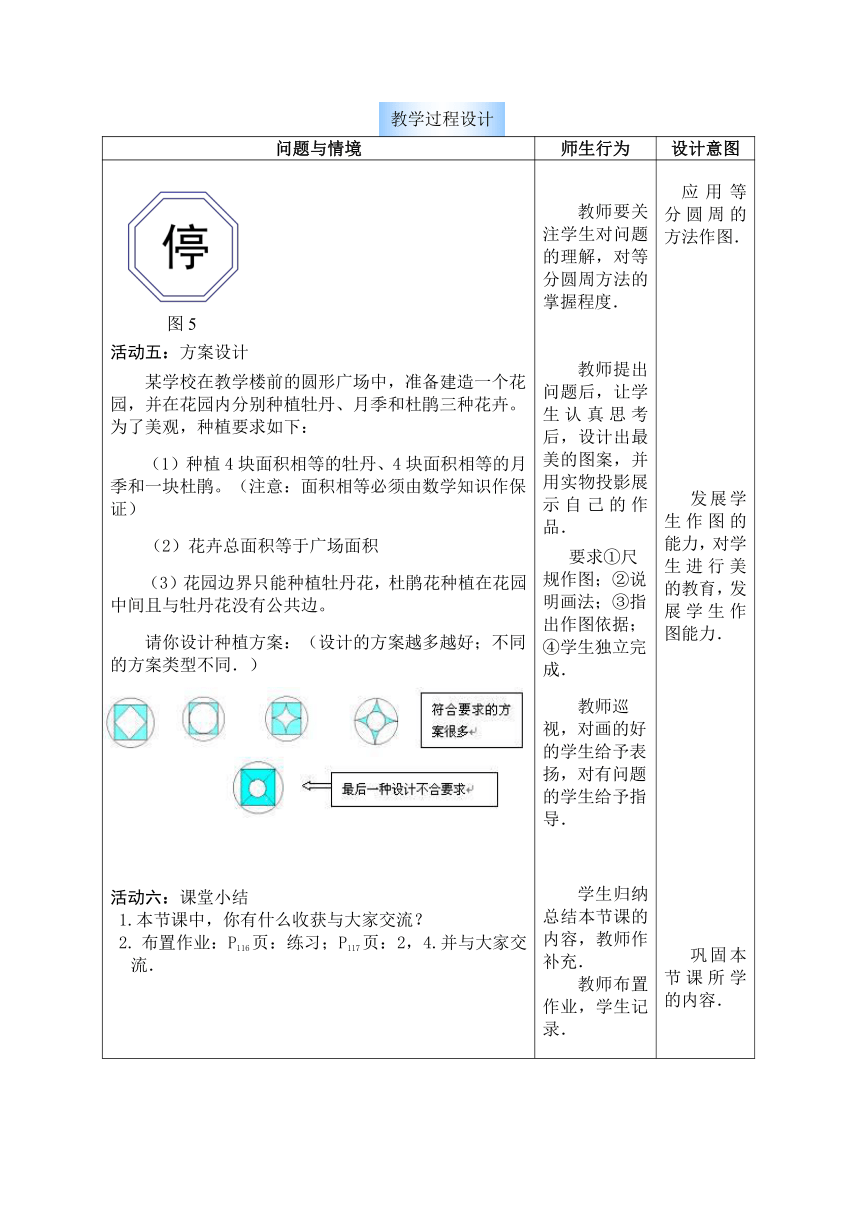
活动五:方案设计 某学校在教学楼前的圆形广场中,准备建造一个花园,并在花园内分别种植牡丹、月季和杜鹃三种花卉。为了美观,种植要求如下: (1)种植4块面积相等的牡丹、4块面积相等的月季和一块杜鹃。(注意:面积相等必须由数学知识作保证) (2)花卉总面积等于广场面积 (3)花园边界只能种植牡丹花,杜鹃花种植在花园中间且与牡丹花没有公共边。 请你设计种植方案:(设计的方案越多越好;不同的方案类型不同.)活动六:课堂小结 1.本节课中,你有什么收获与大家交流? 2. 布置作业:P116页:练习;P117页:2,4.并与大家交流. 教师要关注学生对问题的理解,对等分圆周方法的掌握程度.教师提出问题后,让学生认真思考后,设计出最美的图案,并用实物投影展示自己的作品.要求①尺规作图;②说明画法;③指出作图依据;④学生独立完成. 教师巡视,对画的好的学生给予表扬,对有问题的学生给予指导.学生归纳总结本节课的内容,教师作补充.教师布置作业,学生记录. 应用等分圆周的方法作图.发展学生作图的能力,对学生进行美的教育,发展学生作图能力.巩固本节课所学的内容.
扩展资料:
1.我国民间相传有五边形的近似画法,画法口诀是:“九五顶五九,八五两边分”,它的意义如图:如果正五边形的边长为10,作它的中垂线,取=15.4,在上取=9.5,则=5.9,过点作,在上取==8.连结、、、即可.
例:用民间相传画法口诀,画边长为20mm的正五边形.
分析:要画边长20mm的正五边形,关键在于计算出口诀中各部分的尺寸,由于要画的正五边形与口诀正五边形相似,所以要画的正五边形的各部分应与口诀正五边形各部分对应成比例.由已知知道要画正五边形的边=20mm.请同学们算出各部分的尺寸,并按口诀画出正五边形.
2.尺规作正五边形
(1) 在⊙O中作互相垂直的两条直径和;
(2) 取半径的中点,以点为圆心,为半径作弧,交于点;
(3) 以点为圆心,为半径作弧,交⊙O于、N;
(4) 分别心M、N为圆心,以AE为半径作弧,交⊙O于P、Q.
则D、M、P、Q、N就是⊙O的五等分点.
3. 小圆覆盖大圆
“覆盖问题”在实际中经常遇到,如三颗同步通信卫星就可以覆盖整个地球,一个物体能否覆盖住另一个物体等等.下面举一个日常生活中的问题:在一场演出中,根据需要必须用灯光照亮舞台中一个半径为2米的圆形区域,但不巧,当时没有这样的灯,舞台监督要求用另一种可照半径l米的灯光代替,使其灯光照到指定区域的每一点.那么这样至少需几盏代用灯?
我们用数学语言叙述即最少需要几个半径为l的圆才能完全覆盖半径为2的圆?(各圆可相互叠放)
设半径为2的圆的圆心是O,在圆周上作正六边形ABCDEF,其边长都是2.再分别以各边中点为圆心作六个半径为l的圆(见图)各圆的圆周除相交于A,B,C,D,E,F
各点外,还相交于Al,Bl,Cl,Dl,El,Fl各点并构成边长为l的正六边形的顶点.涂线部分只要以O为圆心并以半径l作圆即可覆盖,一共要七个圆.
不难看出只用六个小圆是不行的.大圆的圆周必需有六个小圆才能盖满,这时中央的小圆是不可缺少的.
24.3 正多边形和圆(2)
教学目标 知识技能 熟练掌握正三边形、正方形、正六边形的有关计算.
数学思考 通过正多边形的有关计算,培养学生的计算能力,特别是解三角形的能力.
解决问题 通过对例题的研究,发展学生“转化思想”和解题能力.
情感态度 通过对正三边形、正方形、正六边形的研究,揭示正多边形的内在规律,激发学生的兴趣和探究精神.
重点 正三角形、正方形、正六边形的有关计算.
难点 正确地转化和综合应用几何知识准确计算.
正多边形的有关计算六角亭问题的解答 探究活动
问题与情境 师生行为 设计意图
活动一:创设情景,引出新知问题:如图1,这是一个漂亮的六角亭,已知它地基是半径为4m的正六边形,你能求出地基的周长和面积吗?活动二:复习引入 填空:1.正多边形的内角和公式是 ;2.正多边形的每个内角等于 ;3.正多边形的每个外角等于 ;4.正多边形的每个中心角等于 ;5.正多边形的每个内角 它的每个外角.活动三:观察图形,归纳规律 问题1:每个图形的半径,分别将它们分割成什么样的三角形?它们有什么规律?问题2:作每个正多边形的边心距,又有什么规律? 教师提出问题后,学生思考并说明不能解决这个问题,从而引出今天的课题:正多边形的有关计算.教师提出问题后,学生认真思考,回答教师提出的问题.教师关注学生是否在倾听.教师引导学生观察,学生回答. 观察:三角形的形状,三角形的个数. 归纳:正n边形的n条半径分正n边形为n个全等的等腰三角形.教师引导学生观察,学生回答.观察、归纳:这些边心距又把这个等腰三角形分成了个直角三角形,这些直角三角形也是全等的. 由实际问题引出课题,既说明数学知识的应用性,同时由漂亮的六角亭图片激发学生的学习兴趣. 复习原有知识,为今天的学习做好准备.发展学生观察图形、分析问题,归纳规律的能力.发展学生观察图形、分析问题,归纳规律的能力.
问题与情境 师生行为 设计意图
通过师生共同探讨,得出:正多边形的有关计算可以转化为直角三角形的计算. 活动四:解决六角亭的问题: 已知正六边形的半径为4米,求这个正六边形的边长、周长和面积. 教师引导学生观察六角亭,并把它转化为正多边形的有关计算.教师引导学生分析解题思路: ,由半径a6 、r6. P6、S6. 解: 连结OA、OB;过O作OG⊥AB,垂足为G,得Rt△OGA. ∴ ∵=60° ∴△AOB是等边三角形∴==4,==2在中,由勾股定理得:==∴P6=6·=6×4=24,∴=×4×===2441.6 ∴六角亭的地基周长为24米,面积约为41.6米. 学生完成解题过程,教师关注学生解直角三角形的能力. 教师巡视,对解题能力较弱的学生给予指点,对于做得好的学生给予表扬. 并说明:运用所学知识能解决生活中的很多问题. 将实际问题转化为数学问题,渗透数学建模思想. 培养学生的运算能力和综合运用几何知识的能力.培养学生应用数学的意识.
问题与情境 师生行为 设计意图
活动五:探究活动问题:已知圆的半径为R,求它的内接正三角形、正方形的边长、边心距及面积.活动六:总结收获,布置作业本节课中你最大的收获是什么?请与大家分享. 教师可继续提问:如:若知道六角亭的边心距,你能求出亭子的周长和面积吗?若亭子地基若是正五边形、正四边形或正八边形呢?学生思考教师提出的问题,并进行讨论、交流,教师在此基础上,归纳出解决正多边形有关计算问题的基本方法:解决正多边形的有关计算问题是转化为直角三角形的问题.教师在此基础上指出:正n边形的边长为,半径为,边心距为,中心角为,周长为,面积为.且有:=n, = 在上述问题的基础上,教师引导学生应用上述方法解决新的问题. 学生以小组进行研究,教师指导学生观察各种正多边形的特点,根据特点解答问题,学生写出解题过程,在投影前展示,表扬好的方面,指出不足,在此基础上,教师引导学生归纳出:(1)正六边形的60°,因此可化为六个等边三角形,从而得到:;(2)正三边形(等边三角形)的120°,因此可化为三个30°,30°,120°的等腰三角形, 从而得到:;(3)正四边形(正方形)的90°,因此可化为四个等腰直角三角形,从而得到:.(4)对于这几种正多边形的计算,只要知道边数和其余元素中的一个,就可以求出其它的元素 学生自由发言,发表自己的见解和收获. 由特殊到一般,为今后解直角三角形埋下伏笔. 体现转化思想,教给学生解决问题的方法:化未知为已知,并随时总结所得到的规律. 在教学中随时对学生进行学法指导,教学生知识,更教学生学习的方法. 复习、归纳、总结,巩固本节课所学的知识.
问题与情境 师生行为 设计意图
2.布置作业:A组:(1)P117页:1(写出过程),3;(2)继续完成探究活动;(3)归纳正三边形、正方形、正六边形的有关计算公式.B组:(1)归纳正三角形、正方形、正六边形的有关计算公式. (2)P117页:1,5,6,7,8.课后探究:探究活动 已知下列图形分别为正方形、正五边形、正六边形,试计算角、、的大小. 探究它们存在什么规律?你能证明吗? (提示:) 知识:正三角形、正方形、正六边形的元素的计算问题.思想:转化思想. 能力:计算能力;观察、分析、研究、归纳能力.教师在此基础上指出:对于正三边形、正四边形和正六边形的计算,以及任意正多边形的计算,在以后都会用解直角三角形的方法解决. 教师布置作业,学生记录作业. 为学有余力的学生布置. 为以后的学习打下伏笔. 巩固本节课所学的知识.把课上的知识延伸到课下.
图3
教学过程设计
教学过程设计
图5
教学任务分析
板书设计
课后反思
教学过程设计
图2
图1
教学过程设计
图4
教学任务分析
板书设计
课后反思
教学过程设计
图1
教学过程设计
教学过程设计
教学过程设计
教学目标 知识技能 使学生经历正多边形的形成过程,了解正多边形的有关概念,掌握用等分圆周画圆的内接正多边形的方法.
数学思考 使学生丰富对正多边形的认识,通过设计图案,发展学生的形象思维.
解决问题 使学生会等分圆周,利用等分圆周的方法构造正多边形,并会设计图案,发展学生的实践能力和创新精神.
情感态度 通过等分圆周、构造正多边形等实践活动,使学生在数学学习活动中获得成功的体验,建立自信心.
重点 了解圆与正多边形的关系;掌握用量角器等分圆心角来等分圆,从而得到正多边形和尺规作圆内接正方形和正六边形的方法.
难点 对正n边形中“n”的接受和理解.
正多边形和圆正多边形的概念:等分圆周的方法:
问题与情境 师生行为 设计意图
活动一:复习提问1.什么样的图形叫做正多边形? 展示图片(课本P113页图片),你还能举出一些这样的例子吗?2.正多边形与圆有什么关系呢? (引出课题)活动二:等分圆周问题:为什么等分圆周就能得到正多边形呢? 教师提出问题,学生进行回答:各边相等,各角相等的多边形叫做正多边形.并举出生活中的例子.教师可再展示一些图片让学生欣赏.学生根据教师提出的问题进行思考,回忆圆的有关知识,进而回答教师提出的问题.即等分圆周,就可以得到圆内接正多边形,这个圆叫做这个正多边形的外接圆.教师提出问题后,学生认真思考、交流,充分发表自己的见解,并互相补充.教师在学生归纳的基础上进行补充,并以正五边形为例进行证明. 复习正多边形的概念,为今天的课程做准备. 激发学生的学习兴趣.培养学生的思维品质,将正多边形与圆联系起来.并由此引出今天的课题.
问题与情境 师生行为 设计意图
活动三:如何等分圆周呢?问题: 已知⊙O的半径为2cm,求作圆的内接正三角形. 教师在学生思考、交流的基础上板书证明过程:如图, ∵ ∴ ∴ 同理可证:∴ 五边形是正五边形. ∵A、B、C、D、E在⊙O上, ∴五边形ABCDE是圆内接正五边形.教师提出问题后,学生思考、交流自己的见解,教师组织学生进行作图,方法不限. 以下为解决问题的参考方案:(上课时教师归纳学生的方法) (1)度量法:①用量角器或30°角的三角板度量,使∠=∠CAO=30°,如图1.②用量角器度量,使∠=∠=∠=120°,如图2.(2)尺规作图:用圆规在⊙O上截取长度等于半径(2cm)的弦,连结、、即可,如图3. (3)计算与尺规作图结合法:由正三角形的半径与边长的关系可得,正三角形的边长= R=2(cm),用圆规在⊙O上截取长度为2(cm)的弦、,连结、、即可. 使学生理解、体会圆与正多边形的内在联系.充分发展学生的发散思维.让学生充分利用手中的工具,实际操作,认真思考,从而培养学生的动手能力.
问题与情境 师生行为 设计意图
在师生共同作图的基础上,归纳出:正多边形与圆有着密切的联系.如:圆既是轴对称图形,又是中心对称图形,且它的每一条直径所在的直线都是它的对称轴,圆具有旋转不变性.正多边形也是轴对称图形,正n边形有n条对称轴,当n为偶数时,它也是中心对称图形,且绕中心旋转,都能和原来的图形重合.结合图4,给出正多边形的中心、半径、中心角、边心距等概念. 同样说明正多边形与圆有着很多内在的联系.活动四:实际应用参照图5,按照一定比例,画一个停车让行的交通标志的外缘. 在学生作图的基础上,教师归纳出等分圆周的方法: 1.用量角器等分圆: 依据:同圆中相等的圆心角所对应的弧相等. 操作:两种情况:其一是依次画出相等的圆心角来等分圆,这种方法比较准确,但是麻烦;其二是先用量角器画一个圆心角,然后在圆上依次截取等于该圆心角所对弧的等弧,于是得到圆的等分点,这种方法比较方便,但画图的误差积累到最后一个等分点,使画出的正多边形的边长误差较大. 2.用尺规等分圆:(1)作正四边形、正八边形. 教师组织学生,分析、作图.归纳:只要做出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……(2)作正六、三、十二边形. 教师组织学生,分析、作图.归纳:先做出正六边形,则可作正三角形,正十二边形,正二十四边形……理论上我们可以一直画下去,但大家不难发现,随着边数的增加,正多边形越来越接近于圆,正多边形将越来越难画.教师提出问题后,学生认真思考,并在笔记本上试着作图,再与同学进行交流. 教给学生等分圆周的方法,尤其是尺规作正方形、正六边形. 使学生体会随着正多边形边数的增多,正多边形越来越接近圆.
问题与情境 师生行为 设计意图
活动五:方案设计 某学校在教学楼前的圆形广场中,准备建造一个花园,并在花园内分别种植牡丹、月季和杜鹃三种花卉。为了美观,种植要求如下: (1)种植4块面积相等的牡丹、4块面积相等的月季和一块杜鹃。(注意:面积相等必须由数学知识作保证) (2)花卉总面积等于广场面积 (3)花园边界只能种植牡丹花,杜鹃花种植在花园中间且与牡丹花没有公共边。 请你设计种植方案:(设计的方案越多越好;不同的方案类型不同.)活动六:课堂小结 1.本节课中,你有什么收获与大家交流? 2. 布置作业:P116页:练习;P117页:2,4.并与大家交流. 教师要关注学生对问题的理解,对等分圆周方法的掌握程度.教师提出问题后,让学生认真思考后,设计出最美的图案,并用实物投影展示自己的作品.要求①尺规作图;②说明画法;③指出作图依据;④学生独立完成. 教师巡视,对画的好的学生给予表扬,对有问题的学生给予指导.学生归纳总结本节课的内容,教师作补充.教师布置作业,学生记录. 应用等分圆周的方法作图.发展学生作图的能力,对学生进行美的教育,发展学生作图能力.巩固本节课所学的内容.
扩展资料:
1.我国民间相传有五边形的近似画法,画法口诀是:“九五顶五九,八五两边分”,它的意义如图:如果正五边形的边长为10,作它的中垂线,取=15.4,在上取=9.5,则=5.9,过点作,在上取==8.连结、、、即可.
例:用民间相传画法口诀,画边长为20mm的正五边形.
分析:要画边长20mm的正五边形,关键在于计算出口诀中各部分的尺寸,由于要画的正五边形与口诀正五边形相似,所以要画的正五边形的各部分应与口诀正五边形各部分对应成比例.由已知知道要画正五边形的边=20mm.请同学们算出各部分的尺寸,并按口诀画出正五边形.
2.尺规作正五边形
(1) 在⊙O中作互相垂直的两条直径和;
(2) 取半径的中点,以点为圆心,为半径作弧,交于点;
(3) 以点为圆心,为半径作弧,交⊙O于、N;
(4) 分别心M、N为圆心,以AE为半径作弧,交⊙O于P、Q.
则D、M、P、Q、N就是⊙O的五等分点.
3. 小圆覆盖大圆
“覆盖问题”在实际中经常遇到,如三颗同步通信卫星就可以覆盖整个地球,一个物体能否覆盖住另一个物体等等.下面举一个日常生活中的问题:在一场演出中,根据需要必须用灯光照亮舞台中一个半径为2米的圆形区域,但不巧,当时没有这样的灯,舞台监督要求用另一种可照半径l米的灯光代替,使其灯光照到指定区域的每一点.那么这样至少需几盏代用灯?
我们用数学语言叙述即最少需要几个半径为l的圆才能完全覆盖半径为2的圆?(各圆可相互叠放)
设半径为2的圆的圆心是O,在圆周上作正六边形ABCDEF,其边长都是2.再分别以各边中点为圆心作六个半径为l的圆(见图)各圆的圆周除相交于A,B,C,D,E,F
各点外,还相交于Al,Bl,Cl,Dl,El,Fl各点并构成边长为l的正六边形的顶点.涂线部分只要以O为圆心并以半径l作圆即可覆盖,一共要七个圆.
不难看出只用六个小圆是不行的.大圆的圆周必需有六个小圆才能盖满,这时中央的小圆是不可缺少的.
24.3 正多边形和圆(2)
教学目标 知识技能 熟练掌握正三边形、正方形、正六边形的有关计算.
数学思考 通过正多边形的有关计算,培养学生的计算能力,特别是解三角形的能力.
解决问题 通过对例题的研究,发展学生“转化思想”和解题能力.
情感态度 通过对正三边形、正方形、正六边形的研究,揭示正多边形的内在规律,激发学生的兴趣和探究精神.
重点 正三角形、正方形、正六边形的有关计算.
难点 正确地转化和综合应用几何知识准确计算.
正多边形的有关计算六角亭问题的解答 探究活动
问题与情境 师生行为 设计意图
活动一:创设情景,引出新知问题:如图1,这是一个漂亮的六角亭,已知它地基是半径为4m的正六边形,你能求出地基的周长和面积吗?活动二:复习引入 填空:1.正多边形的内角和公式是 ;2.正多边形的每个内角等于 ;3.正多边形的每个外角等于 ;4.正多边形的每个中心角等于 ;5.正多边形的每个内角 它的每个外角.活动三:观察图形,归纳规律 问题1:每个图形的半径,分别将它们分割成什么样的三角形?它们有什么规律?问题2:作每个正多边形的边心距,又有什么规律? 教师提出问题后,学生思考并说明不能解决这个问题,从而引出今天的课题:正多边形的有关计算.教师提出问题后,学生认真思考,回答教师提出的问题.教师关注学生是否在倾听.教师引导学生观察,学生回答. 观察:三角形的形状,三角形的个数. 归纳:正n边形的n条半径分正n边形为n个全等的等腰三角形.教师引导学生观察,学生回答.观察、归纳:这些边心距又把这个等腰三角形分成了个直角三角形,这些直角三角形也是全等的. 由实际问题引出课题,既说明数学知识的应用性,同时由漂亮的六角亭图片激发学生的学习兴趣. 复习原有知识,为今天的学习做好准备.发展学生观察图形、分析问题,归纳规律的能力.发展学生观察图形、分析问题,归纳规律的能力.
问题与情境 师生行为 设计意图
通过师生共同探讨,得出:正多边形的有关计算可以转化为直角三角形的计算. 活动四:解决六角亭的问题: 已知正六边形的半径为4米,求这个正六边形的边长、周长和面积. 教师引导学生观察六角亭,并把它转化为正多边形的有关计算.教师引导学生分析解题思路: ,由半径a6 、r6. P6、S6. 解: 连结OA、OB;过O作OG⊥AB,垂足为G,得Rt△OGA. ∴ ∵=60° ∴△AOB是等边三角形∴==4,==2在中,由勾股定理得:==∴P6=6·=6×4=24,∴=×4×===2441.6 ∴六角亭的地基周长为24米,面积约为41.6米. 学生完成解题过程,教师关注学生解直角三角形的能力. 教师巡视,对解题能力较弱的学生给予指点,对于做得好的学生给予表扬. 并说明:运用所学知识能解决生活中的很多问题. 将实际问题转化为数学问题,渗透数学建模思想. 培养学生的运算能力和综合运用几何知识的能力.培养学生应用数学的意识.
问题与情境 师生行为 设计意图
活动五:探究活动问题:已知圆的半径为R,求它的内接正三角形、正方形的边长、边心距及面积.活动六:总结收获,布置作业本节课中你最大的收获是什么?请与大家分享. 教师可继续提问:如:若知道六角亭的边心距,你能求出亭子的周长和面积吗?若亭子地基若是正五边形、正四边形或正八边形呢?学生思考教师提出的问题,并进行讨论、交流,教师在此基础上,归纳出解决正多边形有关计算问题的基本方法:解决正多边形的有关计算问题是转化为直角三角形的问题.教师在此基础上指出:正n边形的边长为,半径为,边心距为,中心角为,周长为,面积为.且有:=n, = 在上述问题的基础上,教师引导学生应用上述方法解决新的问题. 学生以小组进行研究,教师指导学生观察各种正多边形的特点,根据特点解答问题,学生写出解题过程,在投影前展示,表扬好的方面,指出不足,在此基础上,教师引导学生归纳出:(1)正六边形的60°,因此可化为六个等边三角形,从而得到:;(2)正三边形(等边三角形)的120°,因此可化为三个30°,30°,120°的等腰三角形, 从而得到:;(3)正四边形(正方形)的90°,因此可化为四个等腰直角三角形,从而得到:.(4)对于这几种正多边形的计算,只要知道边数和其余元素中的一个,就可以求出其它的元素 学生自由发言,发表自己的见解和收获. 由特殊到一般,为今后解直角三角形埋下伏笔. 体现转化思想,教给学生解决问题的方法:化未知为已知,并随时总结所得到的规律. 在教学中随时对学生进行学法指导,教学生知识,更教学生学习的方法. 复习、归纳、总结,巩固本节课所学的知识.
问题与情境 师生行为 设计意图
2.布置作业:A组:(1)P117页:1(写出过程),3;(2)继续完成探究活动;(3)归纳正三边形、正方形、正六边形的有关计算公式.B组:(1)归纳正三角形、正方形、正六边形的有关计算公式. (2)P117页:1,5,6,7,8.课后探究:探究活动 已知下列图形分别为正方形、正五边形、正六边形,试计算角、、的大小. 探究它们存在什么规律?你能证明吗? (提示:) 知识:正三角形、正方形、正六边形的元素的计算问题.思想:转化思想. 能力:计算能力;观察、分析、研究、归纳能力.教师在此基础上指出:对于正三边形、正四边形和正六边形的计算,以及任意正多边形的计算,在以后都会用解直角三角形的方法解决. 教师布置作业,学生记录作业. 为学有余力的学生布置. 为以后的学习打下伏笔. 巩固本节课所学的知识.把课上的知识延伸到课下.
图3
教学过程设计
教学过程设计
图5
教学任务分析
板书设计
课后反思
教学过程设计
图2
图1
教学过程设计
图4
教学任务分析
板书设计
课后反思
教学过程设计
图1
教学过程设计
教学过程设计
教学过程设计
同课章节目录
