24.1.3

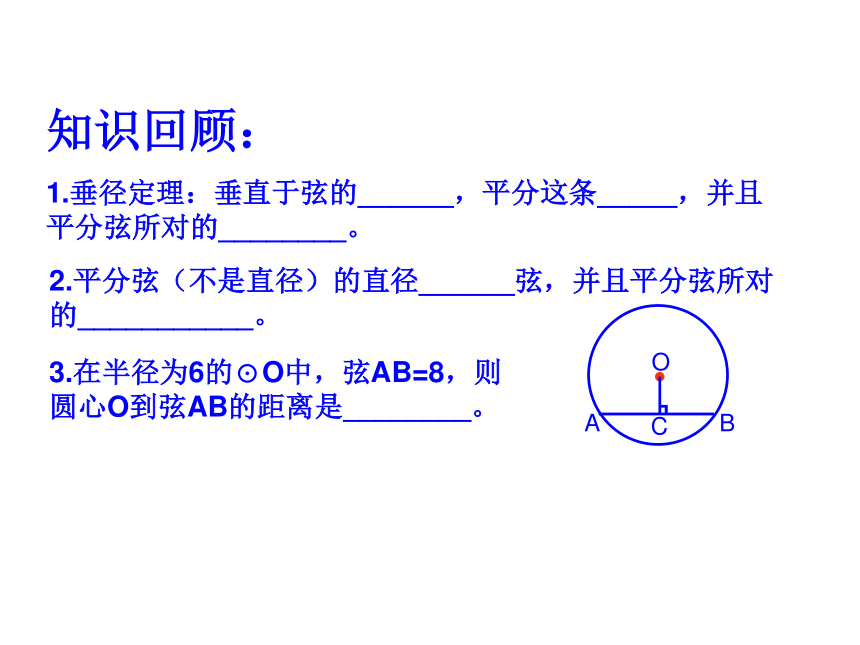
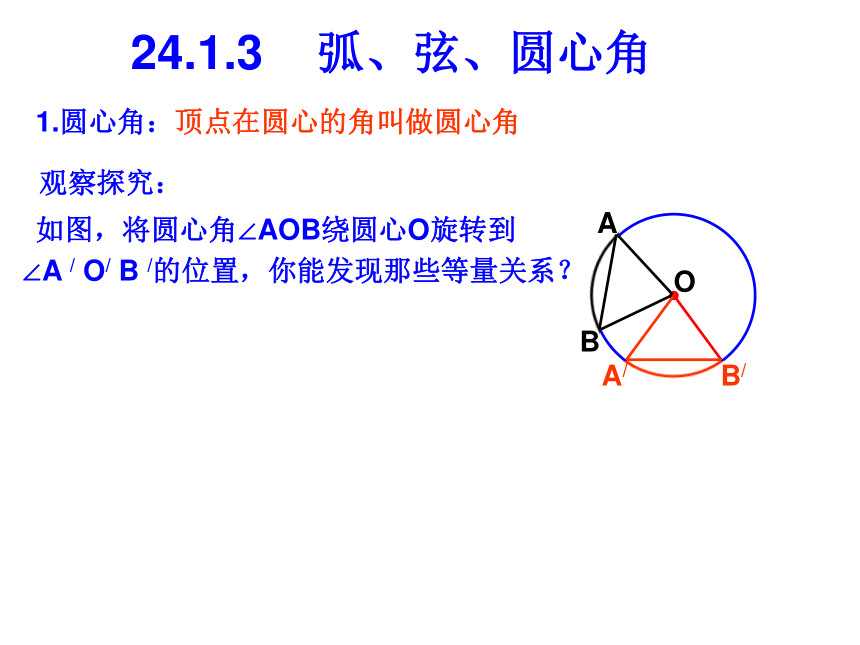
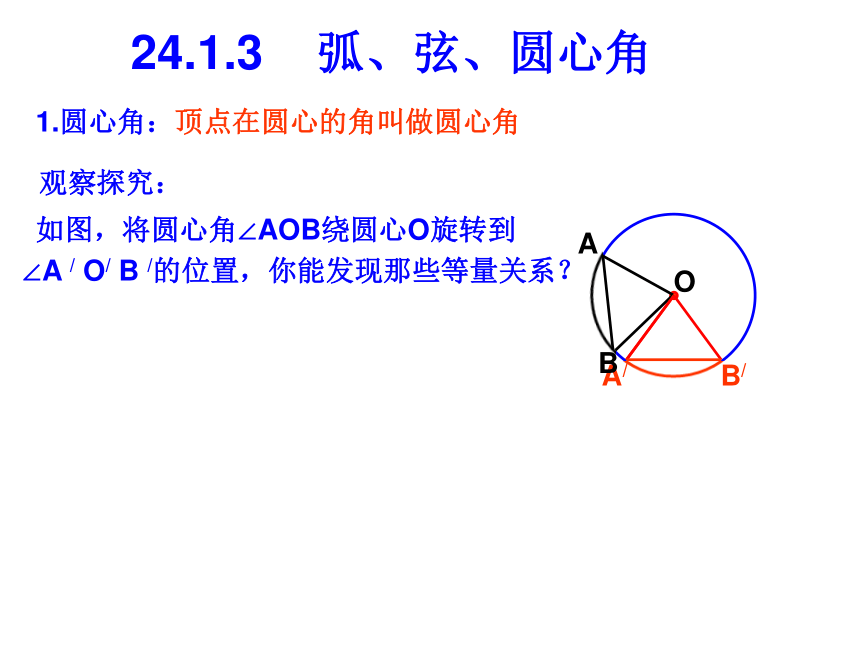
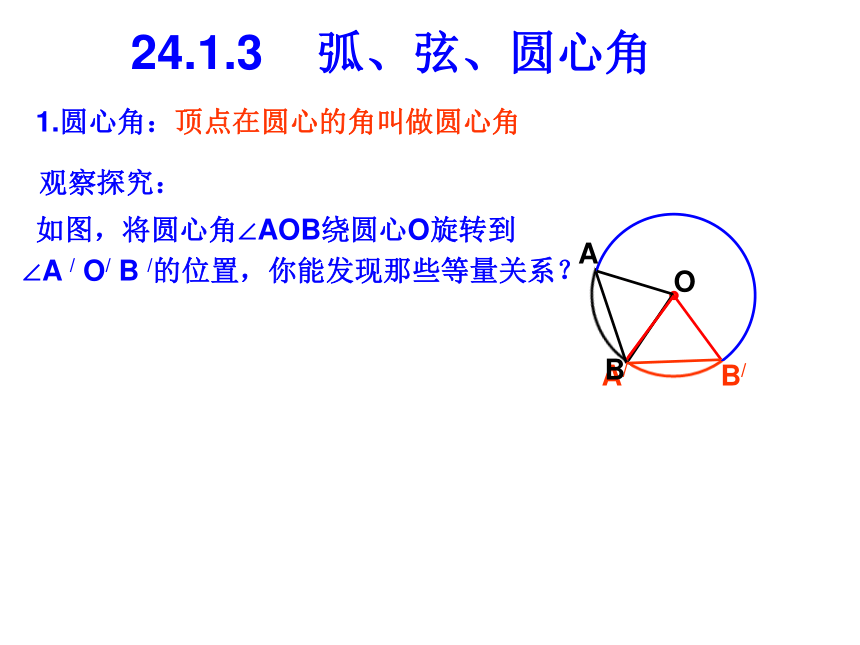
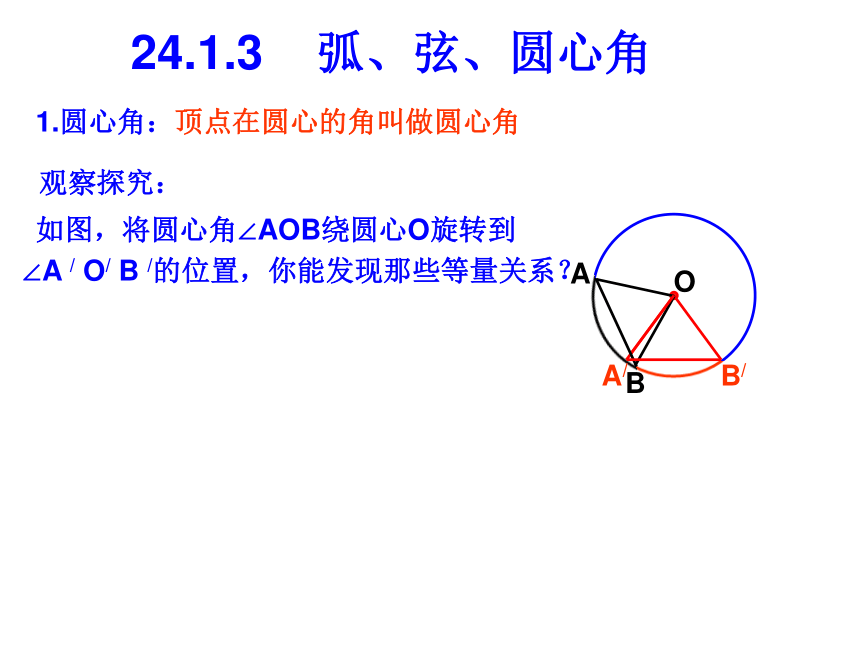
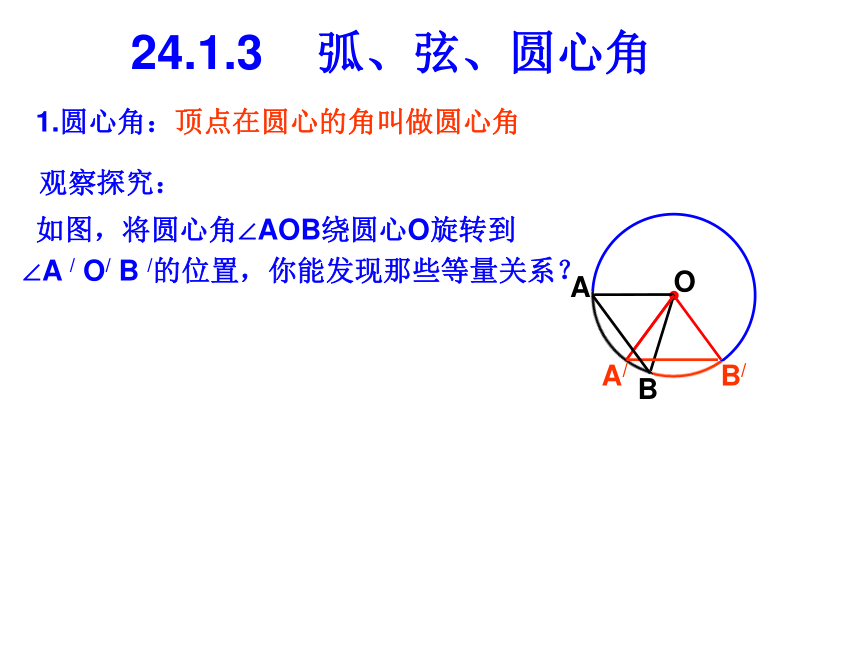
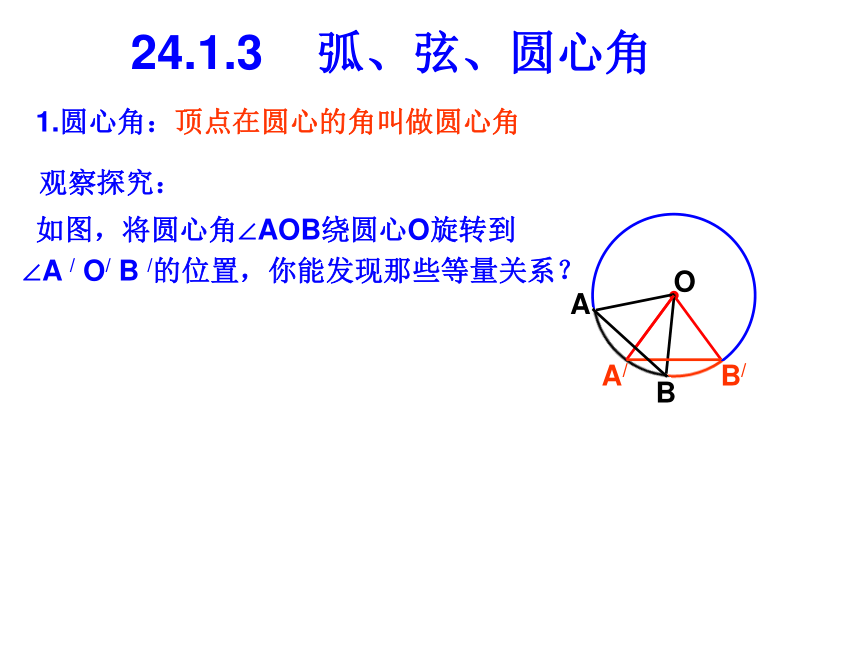
课件20张PPT。大连第十八中学24.1.3 弧、弦、圆心角知识回顾：1.垂径定理：垂直于弦的______，平分这条_____，并且平分弦所对的________。2.平分弦（不是直径）的直径______弦，并且平分弦所对的___________。3.在半径为6的⊙O中，弦AB=8，则圆心O到弦AB的距离是________。我们知道圆是轴对称图形，经过圆心的每一条直线都是它的对称轴。O1.圆心角：24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OAB顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/BA1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/BA1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/BA1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/BA1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角24.1.3 弧、弦、圆心角观察探究：如图，将圆心角∠AOB绕圆心O旋转到∠A / O/ B /的位置，你能发现那些等量关系？OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角在同圆或等圆中24.1.3 弧、弦、圆心角OA/B/AB1.圆心角：顶点在圆心的角叫做圆心角2.弧、弦、圆心角之间的关系定理在同圆或等圆中，如果两个圆心角、两条弧和两条弦中有一组量相等，那么其它两组量都分别相等。3.定理应用举例：例1.如图所示，在⊙O中， ，∠ACB=60°。AB=AC求证：∠AOB=∠BOC=∠AOCOABC即△ABC是等腰三角形又∵ ∠ACB=60°∴△ABC是等边三角形， ∴AB=BC=AC∴ ∠AOB=∠BOC=∠AOC例2.如图所示,在⊙O中，AD=BC.求证:AB=CDOABCD证明：（法一）∴AB=CD∴∠AOD+∠AOC=∠BOC+∠AOC∴∠AOB=∠COD，∴AB＝CD课堂练习：1.如图AB是⊙O的直径， ，∠COD=35°，求：∠AOE的度数。AB=CD=DE2.如图所示，CD为⊙O的弦，在CD上取CE=DF，连结OE、OF，并延长交⊙O于点A、B。
（1）试判断△OEF的形状，并说明理由；（2）求证：AC=BDFODCABE课堂小结：同学们，本堂课，你们都学习了那些新知识？都有哪作业布置：教材87页复习巩固第1题，2题，3题教材88页第11题些收获？