多边形重难点突破(含解析)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 多边形重难点突破(含解析)2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 354.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 19:38:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
多边形重难点突破
突破7 多边形(一) 边
类型一 计算边
1.一个多边形的内角和与它的外角和的比为3:1,则这个多边形的边数为 .
2.一个多边形的内角和比它的外角和的 2倍还大180°,这个多边形的边 数是 .
3.一个多边形的内角和是它的外角和的5倍,则这个多边形是 边形.
4.如果一个多边形的一个内角的外角与其内角的和为600°,那么这个多边形的边数为 .
5.一个多边形截去一个角后,形成的另一个多边形的内角和是 1 440°,则原来多边形的边数是 .
类型二 计算对角线
6.六边形对角线的总条数是( )
A.7条 B.8条 C.9条 D.10条
7.一个多边形的每个外角都等于40°,那么从这个多边形的一个顶点出发的对角线的条数是( )
A.9 条 B.8条 C.7 条 D.6 条
8.一个正多边形的每一个内角都等于135°,那么从这个多边形的一个顶点可以引对角线的条数是( )
A.4 条 B.5 条 C.6条 D.8条
突破8 多边形(二) 角
类型一 多边形的外角和
1.如图,五边形 ABCDE 的一个内角∠BAE=120°,则∠1+∠2+∠3+∠4等于( )
A.100° B.180° C.280° D.300°
类型二 多边形+角平分线
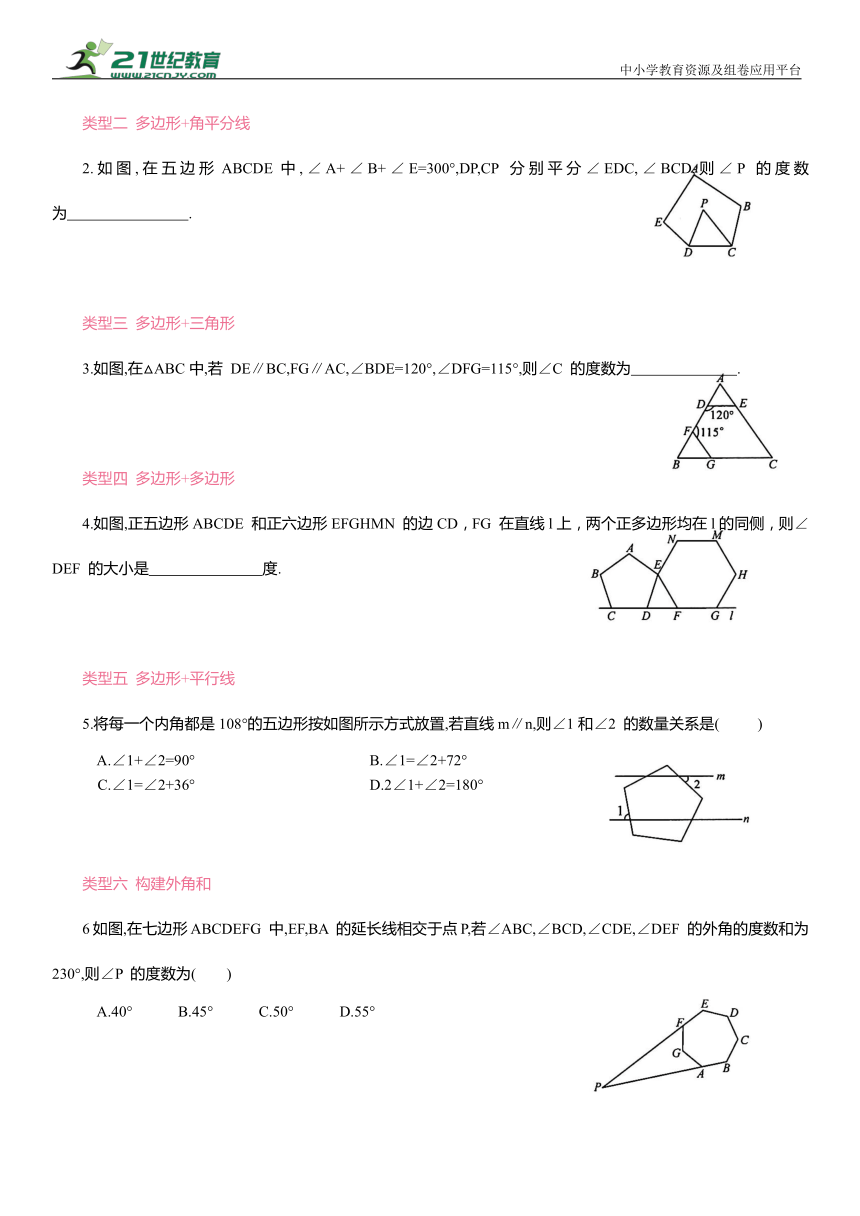
2.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数为 .
类型三 多边形+三角形
3.如图,在△ABC中,若 DE∥BC,FG∥AC,∠BDE=120°,∠DFG=115°,则∠C 的度数为 .
类型四 多边形+多边形
4.如图,正五边形ABCDE 和正六边形EFGHMN 的边CD,FG 在直线l上,两个正多边形均在l的同侧,则∠DEF 的大小是 度.
类型五 多边形+平行线
5.将每一个内角都是108°的五边形按如图所示方式放置,若直线m∥n,则∠1和∠2 的数量关系是( )
A.∠1+∠2=90° B.∠1=∠2+72°
C.∠1=∠2+36° D.2∠1+∠2=180°
类型六 构建外角和
6如图,在七边形ABCDEFG 中,EF,BA 的延长线相交于点P,若∠ABC,∠BCD,∠CDE,∠DEF 的外角的度数和为 230°,则∠P 的度数为( )
A.40° B.45° C.50° D.55°
突破 7 多边形(一) 边
1.8 解:设边数为n,则(n—2)×180°: 360°=3: 1,整理,得n-2=6,解得n=8.
2.7 解:设边数为n,根据题意,得(n-2)×180°=360°× 2+180°,解得 n=7.
3.十二 解:设边数为n,则有(n-2)
·180°=5×360°,解得n=12,
∴这个多边形为十二边形.
4.5 解:设这个外角度数为x,边数为n.根据题意,得(n-2)×180°+x=600°,
解得x=600°-180°n+360°=960°-180°n.由于0因为n为整数,所以n=5.故这个多边形的边数为5.
5.9或10 或11 解:设内角和为 1440°的多边形的边数是n,则(n—2)·180=1440,解得n=10.
则原多边形的边数为9或10或11.
6. C 解:六边形的对角线的条数 n= 故选 C.
7. D 解:多边形的边数为360°÷40°=9,从一个顶点出发可以引对角线的条数为9-3=6(条),故选 D.
8. B 解:∵正多边形的每一个内角都等于135°,
∴每个外角是180°-135°=45°,
∴这个多边形的边数是 360°÷ 45°=8,
∴从这个多边形的一个顶点出发的对角线的条数是5条.故选 B.
突破 8 多边形(二) 角
1. D 解:由图形可知,与∠BAE 相邻的外角的度数为180°—120°=60°,则∠1+∠2+∠3+∠4=360°—60°=300°,故选 D.
2.60° 解:∵在五边形 ABCDE 中,∠A+∠B+∠E=360°,
∴∠EDC+∠BCD=(5-2)×180°-300°=240°.
又∵ DP,CP 分 别平 分 ∠EDC,∠BCD,
∴∠PDC+∠PCD=120°,
∴∠P=180°-(∠PDC+∠PCD)
=180°—120°=60°.故答案为60°.
3.55° 解:∵DE∥BC,∠BDE=120°,
∴∠B=180°-120°=60°.
∵FG∥AC,∠DFG=115°,
∴∠A=180°-115°=65°,
∴∠C=180°-∠B-∠A=55°.
4.48 解:∵五边形ABCDE 是正五边形,
∴∠EDF=72°.
∵六边形 EFGHMN 是正六边形,
∴∠EFD=60°,
∴∠DEF=180°-∠EDF-∠EFD=180°—72°—60°=48°.故答案为48.
5. C 解:如图,延长 DC 交直线 n 于点 H.
由题意,得∠A =∠B =∠DCB=108°,
∴∠GCH=180°-∠DCB=180°-108°=72°.
∵∠1 和∠4是对顶角,
∴∠1=∠4.
∵∠4+∠5+∠A+∠B=360°,
∴∠4+∠5=360°-(∠A+∠B)=360°-(108°+108°)=144°,
∴∠1+∠5=144°,
∴∠5=144°-∠1.
∵∠5与∠CGH 是对顶角,
∴∠5=∠CGH.
∵m∥n,
∴∠2=∠CHG.
又∵∠GCH+∠3+∠CGH=180°,
∴72°+∠2+∠5=180°,
∴∠5=108°-∠2,
∴108°-∠2=144°-∠1,
∴∠1=∠2+36°.故选 C.
6. C 解:如图.
由题意,得∠1+∠2+∠3+∠4=230°,
∴∠5+∠6+∠7=360°—230°=130°.
∵∠8=∠6+∠7,
∴∠5+∠8=130°,
∴∠P=180°-(∠5+∠8)=180°-130°=50°.故选 C.
多边形重难点突破
突破7 多边形(一) 边
类型一 计算边
1.一个多边形的内角和与它的外角和的比为3:1,则这个多边形的边数为 .
2.一个多边形的内角和比它的外角和的 2倍还大180°,这个多边形的边 数是 .
3.一个多边形的内角和是它的外角和的5倍,则这个多边形是 边形.
4.如果一个多边形的一个内角的外角与其内角的和为600°,那么这个多边形的边数为 .
5.一个多边形截去一个角后,形成的另一个多边形的内角和是 1 440°,则原来多边形的边数是 .
类型二 计算对角线
6.六边形对角线的总条数是( )
A.7条 B.8条 C.9条 D.10条
7.一个多边形的每个外角都等于40°,那么从这个多边形的一个顶点出发的对角线的条数是( )
A.9 条 B.8条 C.7 条 D.6 条
8.一个正多边形的每一个内角都等于135°,那么从这个多边形的一个顶点可以引对角线的条数是( )
A.4 条 B.5 条 C.6条 D.8条
突破8 多边形(二) 角
类型一 多边形的外角和
1.如图,五边形 ABCDE 的一个内角∠BAE=120°,则∠1+∠2+∠3+∠4等于( )
A.100° B.180° C.280° D.300°
类型二 多边形+角平分线
2.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数为 .
类型三 多边形+三角形
3.如图,在△ABC中,若 DE∥BC,FG∥AC,∠BDE=120°,∠DFG=115°,则∠C 的度数为 .
类型四 多边形+多边形
4.如图,正五边形ABCDE 和正六边形EFGHMN 的边CD,FG 在直线l上,两个正多边形均在l的同侧,则∠DEF 的大小是 度.
类型五 多边形+平行线
5.将每一个内角都是108°的五边形按如图所示方式放置,若直线m∥n,则∠1和∠2 的数量关系是( )
A.∠1+∠2=90° B.∠1=∠2+72°
C.∠1=∠2+36° D.2∠1+∠2=180°
类型六 构建外角和
6如图,在七边形ABCDEFG 中,EF,BA 的延长线相交于点P,若∠ABC,∠BCD,∠CDE,∠DEF 的外角的度数和为 230°,则∠P 的度数为( )
A.40° B.45° C.50° D.55°
突破 7 多边形(一) 边
1.8 解:设边数为n,则(n—2)×180°: 360°=3: 1,整理,得n-2=6,解得n=8.
2.7 解:设边数为n,根据题意,得(n-2)×180°=360°× 2+180°,解得 n=7.
3.十二 解:设边数为n,则有(n-2)
·180°=5×360°,解得n=12,
∴这个多边形为十二边形.
4.5 解:设这个外角度数为x,边数为n.根据题意,得(n-2)×180°+x=600°,
解得x=600°-180°n+360°=960°-180°n.由于0
5.9或10 或11 解:设内角和为 1440°的多边形的边数是n,则(n—2)·180=1440,解得n=10.
则原多边形的边数为9或10或11.
6. C 解:六边形的对角线的条数 n= 故选 C.
7. D 解:多边形的边数为360°÷40°=9,从一个顶点出发可以引对角线的条数为9-3=6(条),故选 D.
8. B 解:∵正多边形的每一个内角都等于135°,
∴每个外角是180°-135°=45°,
∴这个多边形的边数是 360°÷ 45°=8,
∴从这个多边形的一个顶点出发的对角线的条数是5条.故选 B.
突破 8 多边形(二) 角
1. D 解:由图形可知,与∠BAE 相邻的外角的度数为180°—120°=60°,则∠1+∠2+∠3+∠4=360°—60°=300°,故选 D.
2.60° 解:∵在五边形 ABCDE 中,∠A+∠B+∠E=360°,
∴∠EDC+∠BCD=(5-2)×180°-300°=240°.
又∵ DP,CP 分 别平 分 ∠EDC,∠BCD,
∴∠PDC+∠PCD=120°,
∴∠P=180°-(∠PDC+∠PCD)
=180°—120°=60°.故答案为60°.
3.55° 解:∵DE∥BC,∠BDE=120°,
∴∠B=180°-120°=60°.
∵FG∥AC,∠DFG=115°,
∴∠A=180°-115°=65°,
∴∠C=180°-∠B-∠A=55°.
4.48 解:∵五边形ABCDE 是正五边形,
∴∠EDF=72°.
∵六边形 EFGHMN 是正六边形,
∴∠EFD=60°,
∴∠DEF=180°-∠EDF-∠EFD=180°—72°—60°=48°.故答案为48.
5. C 解:如图,延长 DC 交直线 n 于点 H.
由题意,得∠A =∠B =∠DCB=108°,
∴∠GCH=180°-∠DCB=180°-108°=72°.
∵∠1 和∠4是对顶角,
∴∠1=∠4.
∵∠4+∠5+∠A+∠B=360°,
∴∠4+∠5=360°-(∠A+∠B)=360°-(108°+108°)=144°,
∴∠1+∠5=144°,
∴∠5=144°-∠1.
∵∠5与∠CGH 是对顶角,
∴∠5=∠CGH.
∵m∥n,
∴∠2=∠CHG.
又∵∠GCH+∠3+∠CGH=180°,
∴72°+∠2+∠5=180°,
∴∠5=108°-∠2,
∴108°-∠2=144°-∠1,
∴∠1=∠2+36°.故选 C.
6. C 解:如图.
由题意,得∠1+∠2+∠3+∠4=230°,
∴∠5+∠6+∠7=360°—230°=130°.
∵∠8=∠6+∠7,
∴∠5+∠8=130°,
∴∠P=180°-(∠5+∠8)=180°-130°=50°.故选 C.
