第十三章轴对称(一) 重难点突破 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十三章轴对称(一) 重难点突破 2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 960.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十三章轴对称(一) 重难点突破
突破 1 轴对称(一) 定义与性质
类型一 对称求角度
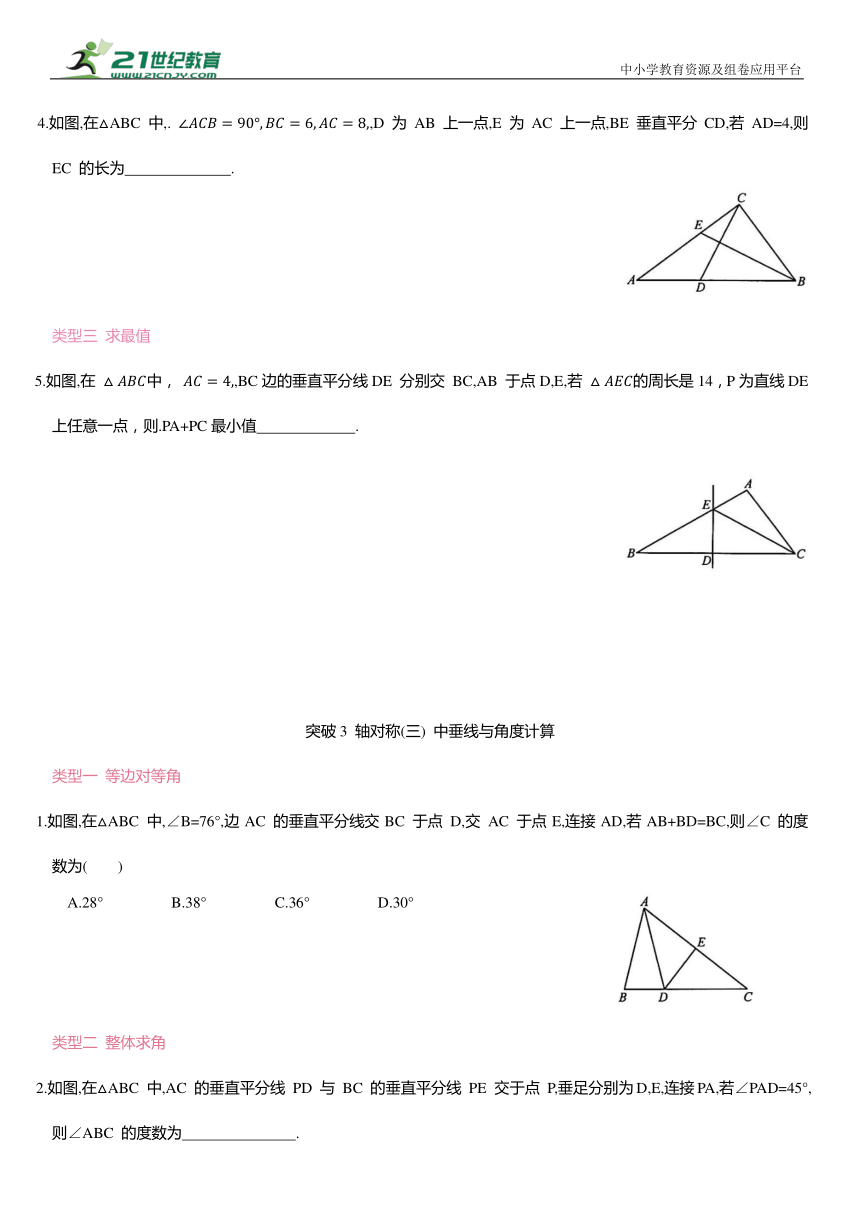
1.如图,在Rt△ABC 中,∠BAC=90°,AD⊥BC,垂足为D,△ADB 与△ADB'关于直线AD 对称,点 B 的对称点是点B',若∠B'AC=14°,则∠B 的度数为( )
A.38° B.48° C.50° D.52°
2.如图,在四边形ABCD 中,AB=AD,点 B 关于AC 的对称点B'恰好落在CD上,若∠BAD=100°,则∠ACB 的度数为 .
类型二 对称求长度
3.如图,在△ABC中,AC=7cm,BC=4cm,将△ABC沿直线l折叠后,点C 恰好落在AB 上的点C',且满足. , l与AC,BC 分别交于 E,F 两点,则△AEC'与△BFC'的周长之差为 cm.
类型三 对称画图
4.如图是由两个阴影的小正方形组成的图形,请你在空白网格中补画一个阴影的小正方形,使补画后的三个阴影图形为轴对称图形,共有 种画法.
5.如图,方格纸中每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,线段AB 的顶点均在格点上.在图中画一条不与AB 重合的线段MN,使MN与AB 关于某条直线对称,且M,N均为格点,这样的线段能画( )
A.2条 B.3条 C.5条 D.6条
突破 2 轴对称(二) 中垂线与长度计算
类型一 整体法
1.如图,在△ABC 中,DE 是AC 的垂直平分线,AE=3,△ABD 的周长为13,△ABC 的周长为( )
A.16 B.13 C.19 D.10
2.如图,在 中, ,垂足为 D,EF 垂直平分AC,交 AC 于点F,交 BC于点E,BD=DE,若△ABC 的周长为26 cm,AF=5cm,则DC 的长为( )
A.8 cm B.7 cm C.10 cm D.9 cm
3.如图,在 中,DE 是 AC 的垂直平分线, 的周长为 21 cm,△ABD 的周长为13 cm,则AE长为 .
类型二 连端点
4.如图,在△ABC 中,. ,D 为AB 上一点,E 为AC 上一点,BE 垂直平分CD,若AD=4,则EC 的长为 .
类型三 求最值
5.如图,在 中, ,BC边的垂直平分线DE 分别交 BC,AB 于点D,E,若 的周长是14,P为直线DE 上任意一点,则.PA+PC最小值 .
突破3 轴对称(三) 中垂线与角度计算
类型一 等边对等角
1.如图,在△ABC 中,∠B=76°,边AC 的垂直平分线交BC 于点 D,交 AC 于点E,连接AD,若AB+BD=BC,则∠C 的度数为( )
A.28° B.38° C.36° D.30°
类型二 整体求角
2.如图,在△ABC 中,AC 的垂直平分线 PD 与 BC 的垂直平分线 PE 交于点 P,垂足分别为D,E,连接PA,若∠PAD=45°,则∠ABC 的度数为 .
3.如图,在△ABC 中,AB 的垂直平分线分别交AB,BC 于点M,P,AC 的垂直平分线分别交AC,BC 于点N,Q.直线MP,NQ 交于点 E,若∠BAC=110°,则∠APE+∠AQE 的度数为 .
4.如图,已知△ABC三内角的角平分线交于点D,三边的垂直平分线交于点E,若∠BEC=132°,则∠BDC= .
突破4 轴对称(四) 中垂线与角平分线
类型一 中垂线+内角平分线
1.如图,在△ABC中,AB 的垂直平分线DE 与∠ACB 的平分线交于点D,E为垂足,DM⊥BC 于点M,DN⊥CA 交CA 的延长线于点N,AB=2DN.
(1)求证:DE=BM;
(2)若AD∥BC,求证:AD=2DE.
类型二 中垂线+外角平分线
2.如图,在△ABC 中,∠ACB=90°,CD 平分∠ACB,交AB 于点D,CM⊥CD,点M 在AB 的垂直平分线上,MH⊥BC 于点H.若BC-AC=5,求CH 的长.
3.如图,在△ABC中,AB>BC,AC 的垂直平分线与△ABC 的外角∠ABE 的平分线交于点 D,连接AD,CD.探究∠ADC 与∠ABD 的数量关系.
突破 1 轴对称(一)
1. D 解:∴ AC=90°,
且∠BAD=∠B'AD,
∴∠BAD=38°,
.故选 D.
2.40° 解:∵点 B 关于AC 的对称点B'恰好落在CD上,
∴∠B=∠AB'C,
∠ACB=∠ACB',
∴∠D+∠B=180°.
∵∠D+∠B+∠DAB+∠BCD=360°,∠DAB=100°,
∴∠BCD=80°,
3.3 解:由折叠知,EC=EC',FC=FC'.
=(CE+AE)--(CF+BF)=AC-BC.
∵AC=7,BC=4,
∴△AEC'与△BFC'的周长之差为3 cm.
4.5 解:如图,①②③④⑤共5种画法.
5. C
中垂线与长度计算
1. C 解:∵DE 是AC 的垂直平分线,∴AD=CD,CE=AE=3,
∴AC=6,
∴AB+BC=AB+BD+CD=AB+BD+AD=13,
∴AB+BC+AC=19.选 C.
2. A 解:∵BD=DE,AD⊥BC,∴AB=AE.
∵EF 垂直平分AC,
∴AE=EC,AC=2AF=10,
∴EC=AE=AB.
∵△ABC 的周长为 26 cm,
∴AB+BC+AC=AB+BD+DE+EC+AC=EC+DE+DE+EC+AC=2DC+AC=26,
∴2DC+10=26,
∴DC=8cm.选 A.
3.4 cm
解:∵DE 是AC的垂直平分线,
∵△ABC 的周长为 21 cm,△ABD的周长为13 cm,
∴AB+BC+AC=21 cm,AB+BD+AD=AB+BD+DC=AB+BC=13 cm,
∴AC=8cm ,
∴AE=4 cm.
4.3 解:连接 ED.
∵BE 垂直平分CD,
∴BD=BC=6,ED=EC.
∵EB=EB,
∴△BEC≌△BED,
∴∠EDB =∠ECB=90°,S△ABC =
+6)·EC,解得 EC=3.
5.10 解:直线 DE 上任意一点 P 到A,C 距离和 PA + PC 最小值为AB.
∵DE 是 BC 的垂直平分线,
∴BE=EC,
则AB=EB+AE=CE+EA.
又∵△ACE 的周长为14,
∴AB=14-4=10,
∴PA+PC 最小值为10.
突破 3 轴对称(三)中垂线与角度计算
1. B 解:∵AB+BD=BC,CD+BD=BC,
∴AB=CD.
∵DE 是 AC 的垂直平分线,
∴DA=DC,
∴AB=AD,
∴∠B=∠ADB=76°.
∵∠ADB =∠C +∠CAD,DA =DC,
故选 B.
2.45° 解:连接 PB,PC.
∵AC 的垂直平分线PD 与 BC 的垂直平分线 PE 交于点 P,
∴PA=PB=PC,
∴∠PCA=∠PAD=45°,∠PAB=∠PBA,∠PCB=∠PBC.
∵∠PCA + ∠PAD + ∠PAB +∠PBA+∠PCB+∠PBC=180°,
∴∠PAB + ∠PBA + ∠PCB +
∴∠PBC+∠PBA=45°,
∴∠ABC=45°.
3.250° 解:∵PM,QN 分别为AB,AC 的垂直平分线,
∴PA=PB,QA=QC,
∴∠B=∠BAP,∠C=∠CAQ.
∵∠BAC=110°,
∴∠B+∠C=180°-∠BAC=70°,
∴∠APE = ∠PAB + ∠AMP =∠B+90°,
∠AQE=∠QAN +∠ANQ=∠C+90°,
∴∠APE+∠AQE=∠B+∠C+
4.123° 解:连接AE.
∵∠BEC=132°,
∴∠EBC+∠ECB=48°,
∴∠ABE + ∠ABE + ∠ACE +∠CAE=180°-(∠EBC+∠ECB)=132°.
∵E 是三边的垂直平分线的交点,
∴EB=EC=EA,
∴∠EAC=∠ECA,∠EBA=∠EAB,
∴∠BAC = ∠EAB + ∠EAC =∠ABE+∠ACE=66°,
∴∠ABC+∠ACB=114°,
∠BCD)=123°.
突破 4 轴对称(四)中垂线与角平分线
1.证明:(1)连接 DB.
∵DE 为AB 的垂直平分线,
∴DB=DA,BE=AE.
∵AB=2DN,
∴BE=AE=DN.
∵CD 平分∠ACB,DM⊥BC,DN⊥AC,
∴DM=DN,
∴BE=AE=DM.
∵DB=DB,
∴Rt△DBE≌Rt△BDM,
∴BM=DE;
(2)延长 DE 交 BC 于点 H.
∵AD∥BC,
∴∠DAE=∠EBH.
∵BE=AE,∠DEA=∠BEH,
∴△ADE≌△BHE,
∴DE=EH.
∵∠DEB=∠DMB=90°,
∴∠MDH=∠HBE,
∴∠DAE=∠MDH.
∵DM=AE,
∴△ADE≌△DHM,
∴AD=DH=2DE.
2.解:过点 M 作 ME⊥AC 交 AC 的延长线于点E,连接BM.
∵CD 平分∠ACB,
∴∠ACD=∠BCD=45°.
∵CM⊥CD,
∴∠BCM=∠ECM.
∵MH⊥BC,ME⊥CE,
∴MH=ME.
∵CM=CM,
∴Rt△CMH≌Rt△CME,
∴CH=CE.
∵点 M 在AB 的垂直平分线上,
∴MA=MB,
∴Rt△AME≌Rt△BMH,
∴BH=AE.
∵BH=BC-CH=AC+CE=AC+CH,
3.解:过点 D 作 DN⊥AB 于点 N,作DM⊥BE 于点M,则∠AND=∠CMD=90°.
∵BD 平分∠ABE,
∴DM=DN.
∵点 D 在 AC 的垂直平分线上,
∴DA=DC.
在 Rt△ADN 和 Rt△CDM 中,DA=DC,DN=DM,
∴Rt△ADN≌Rt△CDM(HL),
∴∠BAD=∠BCD,
∴∠ADC=∠ABC.
∵∠ABE=2∠ABD,
∠ABE+∠ABC=180°,
∴2∠ABD+∠ADC=180°.
第十三章轴对称(一) 重难点突破
突破 1 轴对称(一) 定义与性质
类型一 对称求角度
1.如图,在Rt△ABC 中,∠BAC=90°,AD⊥BC,垂足为D,△ADB 与△ADB'关于直线AD 对称,点 B 的对称点是点B',若∠B'AC=14°,则∠B 的度数为( )
A.38° B.48° C.50° D.52°
2.如图,在四边形ABCD 中,AB=AD,点 B 关于AC 的对称点B'恰好落在CD上,若∠BAD=100°,则∠ACB 的度数为 .
类型二 对称求长度
3.如图,在△ABC中,AC=7cm,BC=4cm,将△ABC沿直线l折叠后,点C 恰好落在AB 上的点C',且满足. , l与AC,BC 分别交于 E,F 两点,则△AEC'与△BFC'的周长之差为 cm.
类型三 对称画图
4.如图是由两个阴影的小正方形组成的图形,请你在空白网格中补画一个阴影的小正方形,使补画后的三个阴影图形为轴对称图形,共有 种画法.
5.如图,方格纸中每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,线段AB 的顶点均在格点上.在图中画一条不与AB 重合的线段MN,使MN与AB 关于某条直线对称,且M,N均为格点,这样的线段能画( )
A.2条 B.3条 C.5条 D.6条
突破 2 轴对称(二) 中垂线与长度计算
类型一 整体法
1.如图,在△ABC 中,DE 是AC 的垂直平分线,AE=3,△ABD 的周长为13,△ABC 的周长为( )
A.16 B.13 C.19 D.10
2.如图,在 中, ,垂足为 D,EF 垂直平分AC,交 AC 于点F,交 BC于点E,BD=DE,若△ABC 的周长为26 cm,AF=5cm,则DC 的长为( )
A.8 cm B.7 cm C.10 cm D.9 cm
3.如图,在 中,DE 是 AC 的垂直平分线, 的周长为 21 cm,△ABD 的周长为13 cm,则AE长为 .
类型二 连端点
4.如图,在△ABC 中,. ,D 为AB 上一点,E 为AC 上一点,BE 垂直平分CD,若AD=4,则EC 的长为 .
类型三 求最值
5.如图,在 中, ,BC边的垂直平分线DE 分别交 BC,AB 于点D,E,若 的周长是14,P为直线DE 上任意一点,则.PA+PC最小值 .
突破3 轴对称(三) 中垂线与角度计算
类型一 等边对等角
1.如图,在△ABC 中,∠B=76°,边AC 的垂直平分线交BC 于点 D,交 AC 于点E,连接AD,若AB+BD=BC,则∠C 的度数为( )
A.28° B.38° C.36° D.30°
类型二 整体求角
2.如图,在△ABC 中,AC 的垂直平分线 PD 与 BC 的垂直平分线 PE 交于点 P,垂足分别为D,E,连接PA,若∠PAD=45°,则∠ABC 的度数为 .
3.如图,在△ABC 中,AB 的垂直平分线分别交AB,BC 于点M,P,AC 的垂直平分线分别交AC,BC 于点N,Q.直线MP,NQ 交于点 E,若∠BAC=110°,则∠APE+∠AQE 的度数为 .
4.如图,已知△ABC三内角的角平分线交于点D,三边的垂直平分线交于点E,若∠BEC=132°,则∠BDC= .
突破4 轴对称(四) 中垂线与角平分线
类型一 中垂线+内角平分线
1.如图,在△ABC中,AB 的垂直平分线DE 与∠ACB 的平分线交于点D,E为垂足,DM⊥BC 于点M,DN⊥CA 交CA 的延长线于点N,AB=2DN.
(1)求证:DE=BM;
(2)若AD∥BC,求证:AD=2DE.
类型二 中垂线+外角平分线
2.如图,在△ABC 中,∠ACB=90°,CD 平分∠ACB,交AB 于点D,CM⊥CD,点M 在AB 的垂直平分线上,MH⊥BC 于点H.若BC-AC=5,求CH 的长.
3.如图,在△ABC中,AB>BC,AC 的垂直平分线与△ABC 的外角∠ABE 的平分线交于点 D,连接AD,CD.探究∠ADC 与∠ABD 的数量关系.
突破 1 轴对称(一)
1. D 解:∴ AC=90°,
且∠BAD=∠B'AD,
∴∠BAD=38°,
.故选 D.
2.40° 解:∵点 B 关于AC 的对称点B'恰好落在CD上,
∴∠B=∠AB'C,
∠ACB=∠ACB',
∴∠D+∠B=180°.
∵∠D+∠B+∠DAB+∠BCD=360°,∠DAB=100°,
∴∠BCD=80°,
3.3 解:由折叠知,EC=EC',FC=FC'.
=(CE+AE)--(CF+BF)=AC-BC.
∵AC=7,BC=4,
∴△AEC'与△BFC'的周长之差为3 cm.
4.5 解:如图,①②③④⑤共5种画法.
5. C
中垂线与长度计算
1. C 解:∵DE 是AC 的垂直平分线,∴AD=CD,CE=AE=3,
∴AC=6,
∴AB+BC=AB+BD+CD=AB+BD+AD=13,
∴AB+BC+AC=19.选 C.
2. A 解:∵BD=DE,AD⊥BC,∴AB=AE.
∵EF 垂直平分AC,
∴AE=EC,AC=2AF=10,
∴EC=AE=AB.
∵△ABC 的周长为 26 cm,
∴AB+BC+AC=AB+BD+DE+EC+AC=EC+DE+DE+EC+AC=2DC+AC=26,
∴2DC+10=26,
∴DC=8cm.选 A.
3.4 cm
解:∵DE 是AC的垂直平分线,
∵△ABC 的周长为 21 cm,△ABD的周长为13 cm,
∴AB+BC+AC=21 cm,AB+BD+AD=AB+BD+DC=AB+BC=13 cm,
∴AC=8cm ,
∴AE=4 cm.
4.3 解:连接 ED.
∵BE 垂直平分CD,
∴BD=BC=6,ED=EC.
∵EB=EB,
∴△BEC≌△BED,
∴∠EDB =∠ECB=90°,S△ABC =
+6)·EC,解得 EC=3.
5.10 解:直线 DE 上任意一点 P 到A,C 距离和 PA + PC 最小值为AB.
∵DE 是 BC 的垂直平分线,
∴BE=EC,
则AB=EB+AE=CE+EA.
又∵△ACE 的周长为14,
∴AB=14-4=10,
∴PA+PC 最小值为10.
突破 3 轴对称(三)中垂线与角度计算
1. B 解:∵AB+BD=BC,CD+BD=BC,
∴AB=CD.
∵DE 是 AC 的垂直平分线,
∴DA=DC,
∴AB=AD,
∴∠B=∠ADB=76°.
∵∠ADB =∠C +∠CAD,DA =DC,
故选 B.
2.45° 解:连接 PB,PC.
∵AC 的垂直平分线PD 与 BC 的垂直平分线 PE 交于点 P,
∴PA=PB=PC,
∴∠PCA=∠PAD=45°,∠PAB=∠PBA,∠PCB=∠PBC.
∵∠PCA + ∠PAD + ∠PAB +∠PBA+∠PCB+∠PBC=180°,
∴∠PAB + ∠PBA + ∠PCB +
∴∠PBC+∠PBA=45°,
∴∠ABC=45°.
3.250° 解:∵PM,QN 分别为AB,AC 的垂直平分线,
∴PA=PB,QA=QC,
∴∠B=∠BAP,∠C=∠CAQ.
∵∠BAC=110°,
∴∠B+∠C=180°-∠BAC=70°,
∴∠APE = ∠PAB + ∠AMP =∠B+90°,
∠AQE=∠QAN +∠ANQ=∠C+90°,
∴∠APE+∠AQE=∠B+∠C+
4.123° 解:连接AE.
∵∠BEC=132°,
∴∠EBC+∠ECB=48°,
∴∠ABE + ∠ABE + ∠ACE +∠CAE=180°-(∠EBC+∠ECB)=132°.
∵E 是三边的垂直平分线的交点,
∴EB=EC=EA,
∴∠EAC=∠ECA,∠EBA=∠EAB,
∴∠BAC = ∠EAB + ∠EAC =∠ABE+∠ACE=66°,
∴∠ABC+∠ACB=114°,
∠BCD)=123°.
突破 4 轴对称(四)中垂线与角平分线
1.证明:(1)连接 DB.
∵DE 为AB 的垂直平分线,
∴DB=DA,BE=AE.
∵AB=2DN,
∴BE=AE=DN.
∵CD 平分∠ACB,DM⊥BC,DN⊥AC,
∴DM=DN,
∴BE=AE=DM.
∵DB=DB,
∴Rt△DBE≌Rt△BDM,
∴BM=DE;
(2)延长 DE 交 BC 于点 H.
∵AD∥BC,
∴∠DAE=∠EBH.
∵BE=AE,∠DEA=∠BEH,
∴△ADE≌△BHE,
∴DE=EH.
∵∠DEB=∠DMB=90°,
∴∠MDH=∠HBE,
∴∠DAE=∠MDH.
∵DM=AE,
∴△ADE≌△DHM,
∴AD=DH=2DE.
2.解:过点 M 作 ME⊥AC 交 AC 的延长线于点E,连接BM.
∵CD 平分∠ACB,
∴∠ACD=∠BCD=45°.
∵CM⊥CD,
∴∠BCM=∠ECM.
∵MH⊥BC,ME⊥CE,
∴MH=ME.
∵CM=CM,
∴Rt△CMH≌Rt△CME,
∴CH=CE.
∵点 M 在AB 的垂直平分线上,
∴MA=MB,
∴Rt△AME≌Rt△BMH,
∴BH=AE.
∵BH=BC-CH=AC+CE=AC+CH,
3.解:过点 D 作 DN⊥AB 于点 N,作DM⊥BE 于点M,则∠AND=∠CMD=90°.
∵BD 平分∠ABE,
∴DM=DN.
∵点 D 在 AC 的垂直平分线上,
∴DA=DC.
在 Rt△ADN 和 Rt△CDM 中,DA=DC,DN=DM,
∴Rt△ADN≌Rt△CDM(HL),
∴∠BAD=∠BCD,
∴∠ADC=∠ABC.
∵∠ABE=2∠ABD,
∠ABE+∠ABC=180°,
∴2∠ABD+∠ADC=180°.
