构造等腰三角形重难点突破 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 构造等腰三角形重难点突破 2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 12:00:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
构造等腰三角形重难点突破
构等腰(一)“两圆一线”画等腰
类型一 无重合点或共线点
1.如图,网格中的每个小正方形的顶点称作格点.图中点 A,B在格点上,则图中满足△ABC 为等腰三角形的格点C 的个数为( )
A.7 B.8 C.9 D.10
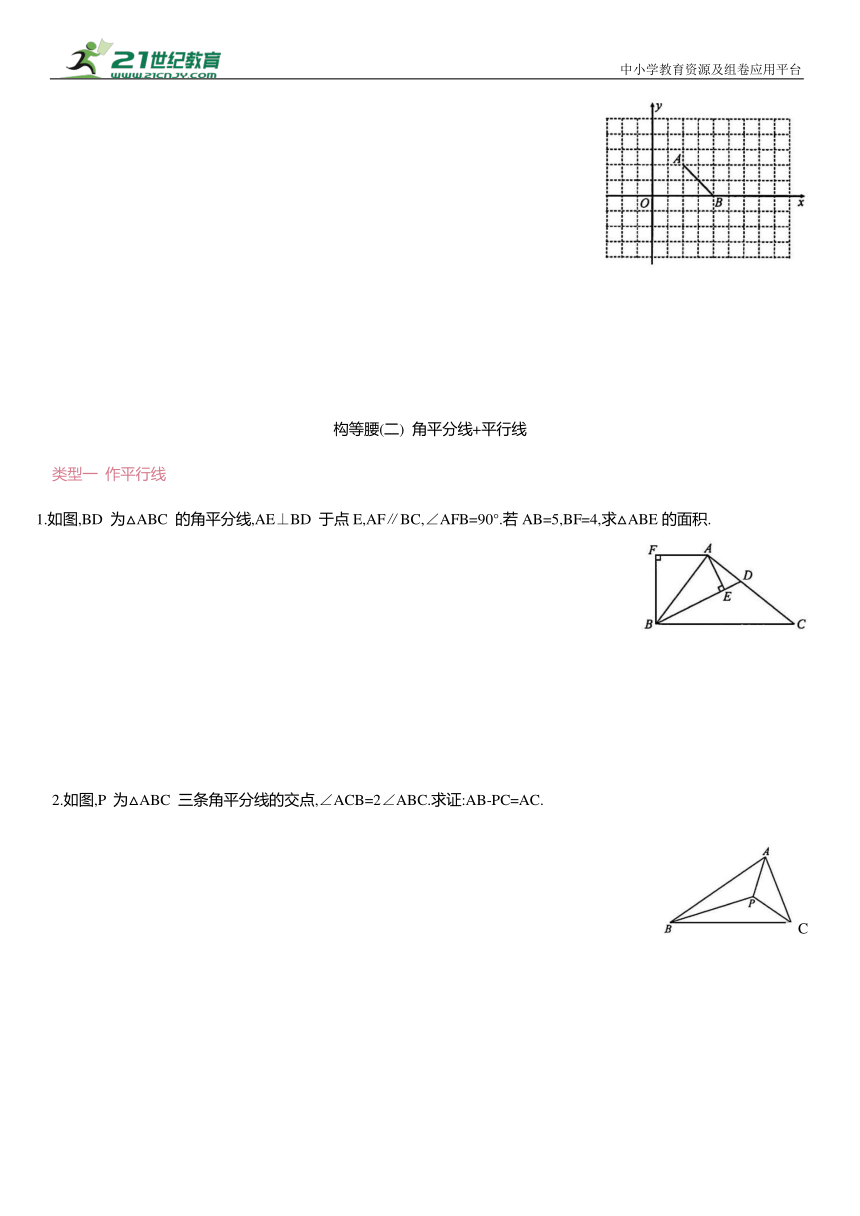
2.在平面直角坐标系中,已知点A(2,-2),在y 轴上确定点 P,使△AOP 为等腰三角形,则符合条件的点 P 共有( )
A.2个 B.3个 C.4个 D.5个
类型二 有重合点或共线点
3.在平面直角坐标系中,已知点 A(-1,0),B(1,1),若在坐标轴上取点 C,使△ABC 为等腰三角形,则满足条件的点C 的个数是( )
A.5 B.6 C.7 D.8
4.已知平面直角坐标系中有A(2,2),B(4,0)两点.若在坐标轴上取点 C,使 为等腰三角形,则满足条件的点 C 的个数是( )
A.5个 B.6个 C.7个 D.8个
构等腰(二) 角平分线+平行线
类型一 作平行线
1.如图,BD 为△ABC 的角平分线,AE⊥BD 于点E,AF∥BC,∠AFB=90°.若AB=5,BF=4,求△ABE的面积.
2.如图,P 为△ABC 三条角平分线的交点,∠ACB=2∠ABC.求证:AB-PC=AC.
C
类型二 隐角平分线
3.如图,△ABC 的两外角平分线交于点 P,过点 P 作AB 的平行线分别交AC,BC于点M,N.
(1)求证:点 P 在∠CAB 的平分线上;
(2)若MN=1,求AM—BN 的值.
构等腰(三) 角平分线+垂线
类型一 延长构
1.如图,在△ABC 中,∠C=3∠B,AD 平分∠BAC 交BC 于点 D,过点 D 作DF⊥AD,交AB 于点F.过点F作FE∥AC,交 BD 于点E,求证:AF=AC+EF.
类型二 作平行构
2.如图,AD 是△BAC 的平分线,且AD=AB,过点C作AD 的垂线,交 AD 的延长线于点 H.用等式表示线段AH 与AB+AC 之间的数量关系,并证明.
类型三 延长+平行构
3.如图,BD 是△ABC 的角平分线,E 是边 BC 上一点,过点 E 作 EF⊥BD 于点F,EF交AC 于点G,且AB+CE=BE.求证:G 为AC的中点.
构等腰(四) 作平行线
类型一 作底的平行线
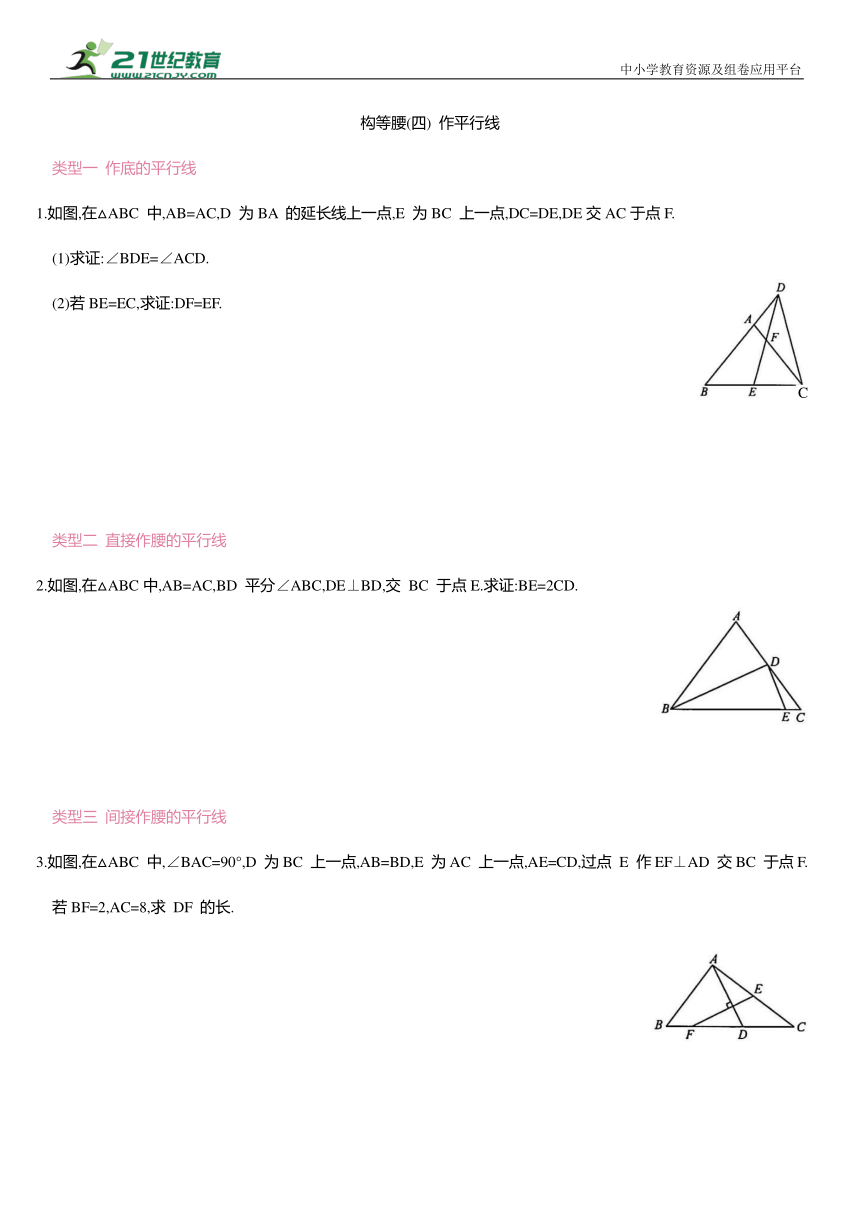
1.如图,在△ABC 中,AB=AC,D 为BA 的延长线上一点,E 为BC 上一点,DC=DE,DE交AC于点F.
(1)求证:∠BDE=∠ACD.
(2)若BE=EC,求证:DF=EF.
C
类型二 直接作腰的平行线
2.如图,在△ABC中,AB=AC,BD 平分∠ABC,DE⊥BD,交 BC 于点E.求证:BE=2CD.
类型三 间接作腰的平行线
3.如图,在△ABC 中,∠BAC=90°,D 为BC 上一点,AB=BD,E 为AC 上一点,AE=CD,过点 E 作EF⊥AD 交BC 于点F.若BF=2,AC=8,求 DF 的长.
构等腰(五) 倍长中线
类型一 倍长中线
1.如图,△ABC 中,D 为BC 的中点,E 是 AD 上一点,连接 BE 并延长交AC于点F,BE=AC,且BF=9,CF=6.求AF 的长.
类型二 倍长类中线
2.如图,在△ABC 中,AB=8,M是BC 的中点,AD 是∠BAC 的平分线,作MF∥AD 交AC于点F.若CF=10,则AC的长为( )
A.12 B.11 C.10 D.9
类型三 证中点
3.如图,在△ABC 中和△DEC 中,∠ACB=∠DCE,AC=BC,CD=CE,∠ADC=90°,延长ED交AB 于点F.求证:F为AB 的中点.
构等腰(六) 二倍角
类型一 明二倍角
1.如图,在 中, D,E 分别在BC,BA 的延长线上, 求证:
2.如图,在 中,AD 平分 ,则 AC的长为( )
A.10 B.11 C.12 D.15
3.如图,在 中, ,沿过点 A 的直线折叠这个三角形,使点B 落在 AC 边上的点E 处,折痕为 AD,
(1)求 的值;
(2)求 DE 的长.
类型二 形外构等腰
4.如图,BD 是△ABC 的中线,∠ABD=2∠CBD,AE⊥BD 于点 E.求证:AB=2DE.
类型三 隐二倍角
5.如图,CD 是△ABC 的高,∠B=23°,∠A=46°.求证:BD=AD+AC.
6. (1)如图1,在△ABC中,∠A=40°,∠C=80°,BD平分∠ABC,交AC于点 D,CD=4,BC=7,求AB 的长;
(2)如图2,在△ABC中,AB=AC,∠A=20°,BD平分∠ABC,交AC 于点D,BD=3,BC=a,用含 a 的式子表示AD 的长.
构等腰(七) 截长补短
类型一 补短
1.如图,△ABC 中,∠ACB=80°,点 D 在BC 上,∠ADC=70°,若AB=AC+CD,则∠BAD 的度数为( )
A.35° B.40° C.30° D.36°
2.如图,在 Rt△ABC 中,∠BAC=90°,点 D 在边 BC 上,AB=AD,点 E 在线段BD 上,∠BAE=3∠EAD.
(1)求证:∠C=2∠EAD;
(2)探究 BE,CD 与AC 的数量关系,并说明理由.
类型二 截长
3.如图,在平面直角坐标系中,O(0,0),A(m,3),B(n,0),其中m,n满足
(1)直接写出△OAB 的形状;
(2)BM平分∠ABO,AD⊥BM 于点 F,交OB 于点D,求 的值.
突破 14 构等腰(一)“两圆一线”画等腰
1. B 解:如图所示,分三种情况:
①以点 A 为圆心,AB 长为半径画弧,则圆弧经过的格点C ,C ,C 即为点 C 的位置;
②以点 B 为圆心,AB 长为半径画弧,则圆弧经过的格点C ,C ,C ,C ,C 即为点 C 的位置;
③作AB 的垂直平分线,垂直平分线没有经过格点,选B.
2. C 解:∵A(2,-2),
∴OA 与y轴的夹角为 45°.
①以点 O 为圆心,OA 长为半径画圆,与y 轴有两个交点;
②以点 A 为圆心,OA 长为半径画圆,与y 轴有两个交点,其中一个是原点(不合题意);
③OA 的垂直平分线与y 轴只有一个交点,这些点不重合.
∴故选 C.
3. D 解:AB 与y 轴的交点即为AB的中点M.
①以点 A 为圆心,AB 长为半径画圆,与坐标轴交于点 C ,C ,C ,C ;
②以点 B 为圆心,BA 长为半径画圆,与坐标轴交于点 C ,C ,C ,A(舍);
③AB的垂直平分线与坐标轴交于点M(舍)和点C .
综上所述,符合条件的点 C 共有 8个.故选 D.
4. A 解:当AB=AC时,以点 A 为圆心,AB长为半径画弧,交y 轴于点C ,C ;当 BA=BC时,以点 B 为圆心,AB长为半径画弧,交x 轴于点C ,C ;当 CA=CB 时,作 AB 的垂直平分线,交x 轴于点C ,交y 轴于点 C .
∵点A,B,C 三个点在同一条直线上,
∴满足条件的点 C 的个数是5.故选A.
1.解:FA 的延长线与BD 的延长线交于点M.
∵BD 平分∠ABC,
∴∠ABD=∠CBD.
∵AM∥BC,
∴∠M=∠DBC,
∴∠ABD=∠M,
∴AM=AB=5.
∵AE⊥BD,
∴BE=EM,
=10,
∴S△ABE=5.
2.证明:过点 P 作 PE∥BC 交 AB 于点E,
∴∠EPB=∠PBC,
∠AEP=∠ABC.
∵BP 平分∠ABC,
∴∠PBC=∠ABP,
∴∠EPB=∠ABP,
∴BE=PE.
∵CP 平分∠ACB,
∴∠ACB=2∠ACP.
∵∠ACB=2∠ABC,
∴∠ACP=∠ABC,
∴∠AEP=∠ACP.
∵AP 平分∠BAC,
∴∠BAP=∠CAP,
∴△APE≌△APC,
∴AE=AC,PE=PC=BE,
∴AB-PC=AB-BE=AE=AC.
3.解:(1)过点 P 分别作AC,AB,BC的垂线,垂足分别为E,F,H.
∵P 为△ABC 的外角平分线的交点,
∴PE=PH,PH=PF,
∴PE=PF.
∵PE⊥AC,PF⊥AB,
∴点 P 在∠CAB 的平分线上;
(2)连接AP.
∵ AP 平 分 ∠CAB, BP 平 分∠CBF,
∴∠CAP=∠PAB,∠CBP=∠PBF.
∵PM∥AB,
∴∠MPA=∠PAB,
∠MPB=∠PBF,
∴∠CAP=∠MPA,
∠MPB=∠CBP,
∴AM=MP,NP=BN,
∴AM--BN=MP-NP=MN=1.
突破 16 构等腰(三)角平分线+垂线
1.解:设∠B=α,则∠C=3α,
-4α.
∵AD平分∠BAC,
∵DF⊥AD,
∴∠ADF=90°,
∵∠AFD=∠B+∠BDF,
∴∠BDF=α=∠B,
∴BF=DF.
延长 FD,AC 交于点M.
∵AD⊥DF,
∴∠ADF=∠ADM=90°.
∵AD平分∠BAC,
∴∠FAD=∠MAD.
∵AD=AD,
∴△ADF≌△ADM,
∴AF=AM=AC+CM,FD=DM.
∵FE∥AC,
∴∠EFD=∠M,
∠FED=∠MCD,
∴△EFD≌△CMD,
∴FE=CM,
∴AF=AC+EF.
2.解:AB+AC=2AH.证明如下:
过点 C 作 CP∥AB,交 AH 的延长线于点P,
∴∠B=∠PCD,∠P=∠BAD.
∵AB= AD,
∴∠B=∠ADB,
∵∠ADB=∠PDC,
∴∠PDC=∠PCD,
∴PD= PC.
∵AD 是∠BAC 的平分线,
∴∠BAD=∠CAD.
∵∠P=∠BAD,
∴∠P=∠CAP.
∵CA=CP,
∴AC=PD,
∴AB+AC=AD+ PD= AP=2AH.
3.解:延长EF,BA 交于点 H,过点 A作AM∥BC 交 HE 于点M.
∵BF⊥EF,
∴∠BFE=∠BFH=90°.
∵BF=BF,∠HBF=∠EBF,
∴△BFH≌△BFE,
∴BH=BE,∠H=∠BEH.
∵BE=AB+CE,BH=AB+AH,
∴CE=AH.
∵AM∥BC,
∴∠AMH=∠BEH,
∴∠AMH=∠H,
∴AM=AH=CE.
∵AM∥EC,
∴∠MAG=∠C.
∵∠AGM=∠CGE,
∴△AMG≌△CEG,
∴AG=CG,
∴G为AC 的中点.
突破17 构等腰(四) 作平行线
1.证明:(1)∵AB=AC,DE=DC,
∴∠B=∠ACB,∠DEC=∠DCE.
∵∠DEC=∠BDE+∠B,∠DCE
=∠ACD+∠ACB,
∴∠BDE=∠ACD;
(2)过点 D 作 DM∥BC 交CA 的延长线于点M,
∴∠M=∠ACB=∠B.
又∵∠BDE=∠ACD,DC=DE,
∴△MCD≌△BDE,
∴MD=BE=EC.
∵MD∥BC,可证△MDF≌△CEF,
∴DF=EF.
2.证明:过点 D 作 DF∥AB,交 BC 于点F,
∴∠ABD=∠BDF.
∵AB=AC,BD 平分∠ABC,
∴∠ABC=∠C,∠ABD=∠DBC,
∴∠DBF=∠BDF,∠DFC=∠C,
∴BF=DF=CD.
∵∠BDE=90°,
∴∠DBE + ∠DEF = ∠BDF +∠FDE=90°,
∴∠DEF=∠FDE,
∴BF=DF=FE,
∴BE=2DF=2DC.
3.解:过点 C 作 AC 的垂线交 AD 的延长线于点 H,延长AB,EF 交于点G.
∵∠BAC=90°,
∴AG∥CH,
∴∠H=∠BAD.
∵BA=BD,
∴∠BAD=∠BDA=∠CDH,
∴∠H=∠CDH,
∴CH=CD=AE.
可证△AGE≌△CAH,
∴AG=AC=8,∠CAH=∠G.
∵EF⊥AD,
∴∠EFD+∠BDA=90°.
∵∠BAD+∠CAH=90°,
∴∠EFD=∠CAH=∠G.
∵∠EFC=∠BFG,
∴∠G=∠BFG,
∴BG=BF=2,
∴BD=AB=AG-BG=8-2=6,
∴DF=BD-BF=4.
突破18 构等腰(五) 倍长中线
1.解:延长 AD 到点G,使 DG=AD,连接 BG.
在△ACD 与△GBD 中,CD=BD,∠ADC=∠BDG,AD=DG,
∴△ACD≌△GBD,
∴∠CAD=∠G,AC=BG.
∵BE=AC,
∴BE=BG,
∴∠G=∠BEG.
∵∠BEG=∠AEF,
∴∠AEF=∠EAF,
∴EF=AF,
∴AF+CF=BF--EF=BF--AF,即AF+6=9-AF,
2. A 解:延长 FM 到点 N,使 MN=MF,连接 BN,延长 MF 交BA 的延长线于点 E,则△BMN≌△CMF,
∴BN=CF,∠N=∠MFC.
又∵∠BAD=∠CAD,MF∥AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB
+AE+FC=BE+FC=BN+FC=2FC.
∵AB=8,CF=10,
∴AC=2FC--AB=20-8=12.
选 A.
3.证明:过点 A 作 AG∥BE 交 EF 的延长线于点G.
∵∠ACB=∠DCE,
∴∠ACD=∠BCE.
∵CA=CB,CD=CE,
∴△CAD≌△CBE,
∴BE = AD,∠CEB = ∠ADC =90°,
∴ ∠CDE + ∠ADF = ∠CED +∠BEF=90°.
∵CE=CD,
∴∠CDE=∠CED,
∴∠ADF=∠BEF.
∵AG∥BE,
∴∠G=∠BEF,
∴∠ADF=∠G,
∴AD=AG.
∵AD=BE,
∴AG=BE.
∵∠EFB=∠AFG,
∴△EFB≌△GFA,
∴AF=BF,
∴F 为AB 的中点.
突破19 构等腰(六) 二倍角
1.证明:过点 D 作 DF⊥AE 于点 F.
∵∠BAC=90°,
∴AC⊥AB.
∵DF⊥AE,
∴DF∥AC,
∴∠CAD=∠ADF.
又∵∠ADE=∠ADF+∠EDF =2∠CAD,
∴∠EDF=∠ADF.
又∵∠EFD=∠AFD=90°,
∴∠FED=∠FAD,
∴DA=DE.
2. B 解:在 AC 上截取AE=AB,连接 DE.
∵AD平分∠BAC,
∴∠BAD=∠DAC.
在△ABD 和△AED 中,AE=AB,∠BAD=∠DAC,AD=AD,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,∠ADB=∠ADE,
BD=DE.
又∠B=2∠ADB,
∴∠AED=2∠ADB.
而 ∠BDE = ∠ADB + ∠ADE =2∠ADB,
∴∠BDE=∠AED,
∴∠CED=∠EDC,
∴CD=CE=7,
∴AC=AE+CE=AB+CD=4+7
=11.故选 B.
3.解:(1)由翻折,得AE=AB=6,
∴CE=AC-AE=3,
(2)∵∠B=2∠ADE,
∠BDE=2∠ADE,
∴∠B=∠BDE.
又∵∠B=∠AED,
∴∠AED=∠EDB,
∴∠CED=∠CDE,
∴CD=CE=3,
∴BD=2.
4.证明:延长EB 至点F,使 BF=AB,连接AF,
过点 C作 CH⊥ED,交 ED 的延长线于点 H.
∵AB=BF,
∴∠ABD=2∠F=2∠CBD,
∴∠F=∠CBD.
∵AD=CD,∠AED=∠H=90°,∠ADE=∠CDH,
∴△ADE≌△CDH,
∴DE=DH,AE=CH,
∴△AEF≌△CHB,
∴FE=BH,
∴BF=EH=2DE,
∴AB=2DE.
5.证明:在 DB 上截取DE=AD,连接CE.
∵CD⊥AB,
∴CA=CE,
∴∠CEA=∠A=46°,
∴∠ECB=∠CEA-∠B=23°,
∴∠ECB=∠B,
∴CE=EB,
∴CA=CE=EB,
∴BD=DE+EB=AD+AC.
6.解:(1)在 BA 上截取BE=BC=7,连接 DE.
∵BD平分∠ABC,
∴∠EBD=∠CBD.
∵BD=BD,
∴△EBD≌△CBD,
∴ED=CD=4,
∠BED=∠C=80°.
∵∠A=40°,
∴∠ADE=∠BED-∠A=40°,
∴∠A=∠EDA,
∴AE=ED=4,
∴AB=BE+AE=7+4=11;
(2)在 BA 上截取 BE=BC=a,在DA 上截取DF=DB=3,连接EF.
∵AB=AC,∠A=20°,
∴∠ABC=∠ACB=80°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=40°.
∵BD=BD,
∴△BCD≌△BED,
∴∠BED=∠C=80°,∠BDE=∠BDC=60°,
∴∠EDF=60°,
∴△BDE≌△FDE,
∴∠EFD=∠EBD=40°,EF=BE=a,
∴∠AEF=∠EFD--∠A=40°-
∴∠AEF=∠A,
∴AF=EF=a,
∴AD=AF+DF=a+3.
突破 20 构等腰(七) 截长补短
C 解:∵∠ACB =80°,∠ADC =70°,
∴∠DAC=180°-80°-70°=30°.
延长 DC 至 点 H,使 CH = AC,
∴∠HAD=∠CAH+∠CAD=70°=∠ADC,
∴HA = HD = HC+ CD = AC +CD.
∵AB=AC+CD,
∴AB=AH=DH,
∴∠B=∠H=40°,
∴∠BAD=70°-40°=30°.故选 C.
2.解:(1)设∠EAD=x,
则∠BAE=3x,
∴∠BAD=4x.
∵AB=AD,
∴∠B=∠ADB=90°-2x.
∵∠BAC=90°,
∴∠C=90°-∠B=2x,
∴∠C=2∠EAD;
(2)AC = CD + BE. 理由如下:在DB 上截取DF=BE,则 DE=BF.
∵AB=AD,∠B=∠ADB,
∴△ABF≌△ADE,
∴AF=AE,
∴∠AFE=∠AEF,
∠BAF=∠EAD=x,
∴∠FAC=90°-x,∠EAF=2x,
∴∠AEF=∠AFE=90°-x,
∴∠FAC=∠AFE,
∴AC=CF=CD+DF=CD+BE.
3.解:(1)等腰直角三角形;
(2)在 FB 上截取 FE = AF,连接AE.
∵AD⊥BM,
∴∠FAE=∠AEF=45°.
∵∠ABO=45°,BF 平分∠ABO,
∴∠ABM=∠OBM=22.5°.
∵∠MAB=90°,
∴∠AMB=67.5°,
∴∠MAF=90°-∠AMB=22.5°,
∴∠MAE=∠MAF+∠FAE=67.5°,∠EAB=90°-∠MAF--∠FAE=22.5°,
∴∠EAB=∠ABM,
∠AMB=∠MAE,
∴ME=AE=EB,
∴AF+MF=EF+MF=ME=AE=BE,
∴BM=2BE,
构造等腰三角形重难点突破
构等腰(一)“两圆一线”画等腰
类型一 无重合点或共线点
1.如图,网格中的每个小正方形的顶点称作格点.图中点 A,B在格点上,则图中满足△ABC 为等腰三角形的格点C 的个数为( )
A.7 B.8 C.9 D.10
2.在平面直角坐标系中,已知点A(2,-2),在y 轴上确定点 P,使△AOP 为等腰三角形,则符合条件的点 P 共有( )
A.2个 B.3个 C.4个 D.5个
类型二 有重合点或共线点
3.在平面直角坐标系中,已知点 A(-1,0),B(1,1),若在坐标轴上取点 C,使△ABC 为等腰三角形,则满足条件的点C 的个数是( )
A.5 B.6 C.7 D.8
4.已知平面直角坐标系中有A(2,2),B(4,0)两点.若在坐标轴上取点 C,使 为等腰三角形,则满足条件的点 C 的个数是( )
A.5个 B.6个 C.7个 D.8个
构等腰(二) 角平分线+平行线
类型一 作平行线
1.如图,BD 为△ABC 的角平分线,AE⊥BD 于点E,AF∥BC,∠AFB=90°.若AB=5,BF=4,求△ABE的面积.
2.如图,P 为△ABC 三条角平分线的交点,∠ACB=2∠ABC.求证:AB-PC=AC.
C
类型二 隐角平分线
3.如图,△ABC 的两外角平分线交于点 P,过点 P 作AB 的平行线分别交AC,BC于点M,N.
(1)求证:点 P 在∠CAB 的平分线上;
(2)若MN=1,求AM—BN 的值.
构等腰(三) 角平分线+垂线
类型一 延长构
1.如图,在△ABC 中,∠C=3∠B,AD 平分∠BAC 交BC 于点 D,过点 D 作DF⊥AD,交AB 于点F.过点F作FE∥AC,交 BD 于点E,求证:AF=AC+EF.
类型二 作平行构
2.如图,AD 是△BAC 的平分线,且AD=AB,过点C作AD 的垂线,交 AD 的延长线于点 H.用等式表示线段AH 与AB+AC 之间的数量关系,并证明.
类型三 延长+平行构
3.如图,BD 是△ABC 的角平分线,E 是边 BC 上一点,过点 E 作 EF⊥BD 于点F,EF交AC 于点G,且AB+CE=BE.求证:G 为AC的中点.
构等腰(四) 作平行线
类型一 作底的平行线
1.如图,在△ABC 中,AB=AC,D 为BA 的延长线上一点,E 为BC 上一点,DC=DE,DE交AC于点F.
(1)求证:∠BDE=∠ACD.
(2)若BE=EC,求证:DF=EF.
C
类型二 直接作腰的平行线
2.如图,在△ABC中,AB=AC,BD 平分∠ABC,DE⊥BD,交 BC 于点E.求证:BE=2CD.
类型三 间接作腰的平行线
3.如图,在△ABC 中,∠BAC=90°,D 为BC 上一点,AB=BD,E 为AC 上一点,AE=CD,过点 E 作EF⊥AD 交BC 于点F.若BF=2,AC=8,求 DF 的长.
构等腰(五) 倍长中线
类型一 倍长中线
1.如图,△ABC 中,D 为BC 的中点,E 是 AD 上一点,连接 BE 并延长交AC于点F,BE=AC,且BF=9,CF=6.求AF 的长.
类型二 倍长类中线
2.如图,在△ABC 中,AB=8,M是BC 的中点,AD 是∠BAC 的平分线,作MF∥AD 交AC于点F.若CF=10,则AC的长为( )
A.12 B.11 C.10 D.9
类型三 证中点
3.如图,在△ABC 中和△DEC 中,∠ACB=∠DCE,AC=BC,CD=CE,∠ADC=90°,延长ED交AB 于点F.求证:F为AB 的中点.
构等腰(六) 二倍角
类型一 明二倍角
1.如图,在 中, D,E 分别在BC,BA 的延长线上, 求证:
2.如图,在 中,AD 平分 ,则 AC的长为( )
A.10 B.11 C.12 D.15
3.如图,在 中, ,沿过点 A 的直线折叠这个三角形,使点B 落在 AC 边上的点E 处,折痕为 AD,
(1)求 的值;
(2)求 DE 的长.
类型二 形外构等腰
4.如图,BD 是△ABC 的中线,∠ABD=2∠CBD,AE⊥BD 于点 E.求证:AB=2DE.
类型三 隐二倍角
5.如图,CD 是△ABC 的高,∠B=23°,∠A=46°.求证:BD=AD+AC.
6. (1)如图1,在△ABC中,∠A=40°,∠C=80°,BD平分∠ABC,交AC于点 D,CD=4,BC=7,求AB 的长;
(2)如图2,在△ABC中,AB=AC,∠A=20°,BD平分∠ABC,交AC 于点D,BD=3,BC=a,用含 a 的式子表示AD 的长.
构等腰(七) 截长补短
类型一 补短
1.如图,△ABC 中,∠ACB=80°,点 D 在BC 上,∠ADC=70°,若AB=AC+CD,则∠BAD 的度数为( )
A.35° B.40° C.30° D.36°
2.如图,在 Rt△ABC 中,∠BAC=90°,点 D 在边 BC 上,AB=AD,点 E 在线段BD 上,∠BAE=3∠EAD.
(1)求证:∠C=2∠EAD;
(2)探究 BE,CD 与AC 的数量关系,并说明理由.
类型二 截长
3.如图,在平面直角坐标系中,O(0,0),A(m,3),B(n,0),其中m,n满足
(1)直接写出△OAB 的形状;
(2)BM平分∠ABO,AD⊥BM 于点 F,交OB 于点D,求 的值.
突破 14 构等腰(一)“两圆一线”画等腰
1. B 解:如图所示,分三种情况:
①以点 A 为圆心,AB 长为半径画弧,则圆弧经过的格点C ,C ,C 即为点 C 的位置;
②以点 B 为圆心,AB 长为半径画弧,则圆弧经过的格点C ,C ,C ,C ,C 即为点 C 的位置;
③作AB 的垂直平分线,垂直平分线没有经过格点,选B.
2. C 解:∵A(2,-2),
∴OA 与y轴的夹角为 45°.
①以点 O 为圆心,OA 长为半径画圆,与y 轴有两个交点;
②以点 A 为圆心,OA 长为半径画圆,与y 轴有两个交点,其中一个是原点(不合题意);
③OA 的垂直平分线与y 轴只有一个交点,这些点不重合.
∴故选 C.
3. D 解:AB 与y 轴的交点即为AB的中点M.
①以点 A 为圆心,AB 长为半径画圆,与坐标轴交于点 C ,C ,C ,C ;
②以点 B 为圆心,BA 长为半径画圆,与坐标轴交于点 C ,C ,C ,A(舍);
③AB的垂直平分线与坐标轴交于点M(舍)和点C .
综上所述,符合条件的点 C 共有 8个.故选 D.
4. A 解:当AB=AC时,以点 A 为圆心,AB长为半径画弧,交y 轴于点C ,C ;当 BA=BC时,以点 B 为圆心,AB长为半径画弧,交x 轴于点C ,C ;当 CA=CB 时,作 AB 的垂直平分线,交x 轴于点C ,交y 轴于点 C .
∵点A,B,C 三个点在同一条直线上,
∴满足条件的点 C 的个数是5.故选A.
1.解:FA 的延长线与BD 的延长线交于点M.
∵BD 平分∠ABC,
∴∠ABD=∠CBD.
∵AM∥BC,
∴∠M=∠DBC,
∴∠ABD=∠M,
∴AM=AB=5.
∵AE⊥BD,
∴BE=EM,
=10,
∴S△ABE=5.
2.证明:过点 P 作 PE∥BC 交 AB 于点E,
∴∠EPB=∠PBC,
∠AEP=∠ABC.
∵BP 平分∠ABC,
∴∠PBC=∠ABP,
∴∠EPB=∠ABP,
∴BE=PE.
∵CP 平分∠ACB,
∴∠ACB=2∠ACP.
∵∠ACB=2∠ABC,
∴∠ACP=∠ABC,
∴∠AEP=∠ACP.
∵AP 平分∠BAC,
∴∠BAP=∠CAP,
∴△APE≌△APC,
∴AE=AC,PE=PC=BE,
∴AB-PC=AB-BE=AE=AC.
3.解:(1)过点 P 分别作AC,AB,BC的垂线,垂足分别为E,F,H.
∵P 为△ABC 的外角平分线的交点,
∴PE=PH,PH=PF,
∴PE=PF.
∵PE⊥AC,PF⊥AB,
∴点 P 在∠CAB 的平分线上;
(2)连接AP.
∵ AP 平 分 ∠CAB, BP 平 分∠CBF,
∴∠CAP=∠PAB,∠CBP=∠PBF.
∵PM∥AB,
∴∠MPA=∠PAB,
∠MPB=∠PBF,
∴∠CAP=∠MPA,
∠MPB=∠CBP,
∴AM=MP,NP=BN,
∴AM--BN=MP-NP=MN=1.
突破 16 构等腰(三)角平分线+垂线
1.解:设∠B=α,则∠C=3α,
-4α.
∵AD平分∠BAC,
∵DF⊥AD,
∴∠ADF=90°,
∵∠AFD=∠B+∠BDF,
∴∠BDF=α=∠B,
∴BF=DF.
延长 FD,AC 交于点M.
∵AD⊥DF,
∴∠ADF=∠ADM=90°.
∵AD平分∠BAC,
∴∠FAD=∠MAD.
∵AD=AD,
∴△ADF≌△ADM,
∴AF=AM=AC+CM,FD=DM.
∵FE∥AC,
∴∠EFD=∠M,
∠FED=∠MCD,
∴△EFD≌△CMD,
∴FE=CM,
∴AF=AC+EF.
2.解:AB+AC=2AH.证明如下:
过点 C 作 CP∥AB,交 AH 的延长线于点P,
∴∠B=∠PCD,∠P=∠BAD.
∵AB= AD,
∴∠B=∠ADB,
∵∠ADB=∠PDC,
∴∠PDC=∠PCD,
∴PD= PC.
∵AD 是∠BAC 的平分线,
∴∠BAD=∠CAD.
∵∠P=∠BAD,
∴∠P=∠CAP.
∵CA=CP,
∴AC=PD,
∴AB+AC=AD+ PD= AP=2AH.
3.解:延长EF,BA 交于点 H,过点 A作AM∥BC 交 HE 于点M.
∵BF⊥EF,
∴∠BFE=∠BFH=90°.
∵BF=BF,∠HBF=∠EBF,
∴△BFH≌△BFE,
∴BH=BE,∠H=∠BEH.
∵BE=AB+CE,BH=AB+AH,
∴CE=AH.
∵AM∥BC,
∴∠AMH=∠BEH,
∴∠AMH=∠H,
∴AM=AH=CE.
∵AM∥EC,
∴∠MAG=∠C.
∵∠AGM=∠CGE,
∴△AMG≌△CEG,
∴AG=CG,
∴G为AC 的中点.
突破17 构等腰(四) 作平行线
1.证明:(1)∵AB=AC,DE=DC,
∴∠B=∠ACB,∠DEC=∠DCE.
∵∠DEC=∠BDE+∠B,∠DCE
=∠ACD+∠ACB,
∴∠BDE=∠ACD;
(2)过点 D 作 DM∥BC 交CA 的延长线于点M,
∴∠M=∠ACB=∠B.
又∵∠BDE=∠ACD,DC=DE,
∴△MCD≌△BDE,
∴MD=BE=EC.
∵MD∥BC,可证△MDF≌△CEF,
∴DF=EF.
2.证明:过点 D 作 DF∥AB,交 BC 于点F,
∴∠ABD=∠BDF.
∵AB=AC,BD 平分∠ABC,
∴∠ABC=∠C,∠ABD=∠DBC,
∴∠DBF=∠BDF,∠DFC=∠C,
∴BF=DF=CD.
∵∠BDE=90°,
∴∠DBE + ∠DEF = ∠BDF +∠FDE=90°,
∴∠DEF=∠FDE,
∴BF=DF=FE,
∴BE=2DF=2DC.
3.解:过点 C 作 AC 的垂线交 AD 的延长线于点 H,延长AB,EF 交于点G.
∵∠BAC=90°,
∴AG∥CH,
∴∠H=∠BAD.
∵BA=BD,
∴∠BAD=∠BDA=∠CDH,
∴∠H=∠CDH,
∴CH=CD=AE.
可证△AGE≌△CAH,
∴AG=AC=8,∠CAH=∠G.
∵EF⊥AD,
∴∠EFD+∠BDA=90°.
∵∠BAD+∠CAH=90°,
∴∠EFD=∠CAH=∠G.
∵∠EFC=∠BFG,
∴∠G=∠BFG,
∴BG=BF=2,
∴BD=AB=AG-BG=8-2=6,
∴DF=BD-BF=4.
突破18 构等腰(五) 倍长中线
1.解:延长 AD 到点G,使 DG=AD,连接 BG.
在△ACD 与△GBD 中,CD=BD,∠ADC=∠BDG,AD=DG,
∴△ACD≌△GBD,
∴∠CAD=∠G,AC=BG.
∵BE=AC,
∴BE=BG,
∴∠G=∠BEG.
∵∠BEG=∠AEF,
∴∠AEF=∠EAF,
∴EF=AF,
∴AF+CF=BF--EF=BF--AF,即AF+6=9-AF,
2. A 解:延长 FM 到点 N,使 MN=MF,连接 BN,延长 MF 交BA 的延长线于点 E,则△BMN≌△CMF,
∴BN=CF,∠N=∠MFC.
又∵∠BAD=∠CAD,MF∥AD,
∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,
∴AE=AF,BN=BE,
∴AB+AC=AB+AF+FC=AB
+AE+FC=BE+FC=BN+FC=2FC.
∵AB=8,CF=10,
∴AC=2FC--AB=20-8=12.
选 A.
3.证明:过点 A 作 AG∥BE 交 EF 的延长线于点G.
∵∠ACB=∠DCE,
∴∠ACD=∠BCE.
∵CA=CB,CD=CE,
∴△CAD≌△CBE,
∴BE = AD,∠CEB = ∠ADC =90°,
∴ ∠CDE + ∠ADF = ∠CED +∠BEF=90°.
∵CE=CD,
∴∠CDE=∠CED,
∴∠ADF=∠BEF.
∵AG∥BE,
∴∠G=∠BEF,
∴∠ADF=∠G,
∴AD=AG.
∵AD=BE,
∴AG=BE.
∵∠EFB=∠AFG,
∴△EFB≌△GFA,
∴AF=BF,
∴F 为AB 的中点.
突破19 构等腰(六) 二倍角
1.证明:过点 D 作 DF⊥AE 于点 F.
∵∠BAC=90°,
∴AC⊥AB.
∵DF⊥AE,
∴DF∥AC,
∴∠CAD=∠ADF.
又∵∠ADE=∠ADF+∠EDF =2∠CAD,
∴∠EDF=∠ADF.
又∵∠EFD=∠AFD=90°,
∴∠FED=∠FAD,
∴DA=DE.
2. B 解:在 AC 上截取AE=AB,连接 DE.
∵AD平分∠BAC,
∴∠BAD=∠DAC.
在△ABD 和△AED 中,AE=AB,∠BAD=∠DAC,AD=AD,
∴△ABD≌△AED(SAS),
∴∠B=∠AED,∠ADB=∠ADE,
BD=DE.
又∠B=2∠ADB,
∴∠AED=2∠ADB.
而 ∠BDE = ∠ADB + ∠ADE =2∠ADB,
∴∠BDE=∠AED,
∴∠CED=∠EDC,
∴CD=CE=7,
∴AC=AE+CE=AB+CD=4+7
=11.故选 B.
3.解:(1)由翻折,得AE=AB=6,
∴CE=AC-AE=3,
(2)∵∠B=2∠ADE,
∠BDE=2∠ADE,
∴∠B=∠BDE.
又∵∠B=∠AED,
∴∠AED=∠EDB,
∴∠CED=∠CDE,
∴CD=CE=3,
∴BD=2.
4.证明:延长EB 至点F,使 BF=AB,连接AF,
过点 C作 CH⊥ED,交 ED 的延长线于点 H.
∵AB=BF,
∴∠ABD=2∠F=2∠CBD,
∴∠F=∠CBD.
∵AD=CD,∠AED=∠H=90°,∠ADE=∠CDH,
∴△ADE≌△CDH,
∴DE=DH,AE=CH,
∴△AEF≌△CHB,
∴FE=BH,
∴BF=EH=2DE,
∴AB=2DE.
5.证明:在 DB 上截取DE=AD,连接CE.
∵CD⊥AB,
∴CA=CE,
∴∠CEA=∠A=46°,
∴∠ECB=∠CEA-∠B=23°,
∴∠ECB=∠B,
∴CE=EB,
∴CA=CE=EB,
∴BD=DE+EB=AD+AC.
6.解:(1)在 BA 上截取BE=BC=7,连接 DE.
∵BD平分∠ABC,
∴∠EBD=∠CBD.
∵BD=BD,
∴△EBD≌△CBD,
∴ED=CD=4,
∠BED=∠C=80°.
∵∠A=40°,
∴∠ADE=∠BED-∠A=40°,
∴∠A=∠EDA,
∴AE=ED=4,
∴AB=BE+AE=7+4=11;
(2)在 BA 上截取 BE=BC=a,在DA 上截取DF=DB=3,连接EF.
∵AB=AC,∠A=20°,
∴∠ABC=∠ACB=80°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=40°.
∵BD=BD,
∴△BCD≌△BED,
∴∠BED=∠C=80°,∠BDE=∠BDC=60°,
∴∠EDF=60°,
∴△BDE≌△FDE,
∴∠EFD=∠EBD=40°,EF=BE=a,
∴∠AEF=∠EFD--∠A=40°-
∴∠AEF=∠A,
∴AF=EF=a,
∴AD=AF+DF=a+3.
突破 20 构等腰(七) 截长补短
C 解:∵∠ACB =80°,∠ADC =70°,
∴∠DAC=180°-80°-70°=30°.
延长 DC 至 点 H,使 CH = AC,
∴∠HAD=∠CAH+∠CAD=70°=∠ADC,
∴HA = HD = HC+ CD = AC +CD.
∵AB=AC+CD,
∴AB=AH=DH,
∴∠B=∠H=40°,
∴∠BAD=70°-40°=30°.故选 C.
2.解:(1)设∠EAD=x,
则∠BAE=3x,
∴∠BAD=4x.
∵AB=AD,
∴∠B=∠ADB=90°-2x.
∵∠BAC=90°,
∴∠C=90°-∠B=2x,
∴∠C=2∠EAD;
(2)AC = CD + BE. 理由如下:在DB 上截取DF=BE,则 DE=BF.
∵AB=AD,∠B=∠ADB,
∴△ABF≌△ADE,
∴AF=AE,
∴∠AFE=∠AEF,
∠BAF=∠EAD=x,
∴∠FAC=90°-x,∠EAF=2x,
∴∠AEF=∠AFE=90°-x,
∴∠FAC=∠AFE,
∴AC=CF=CD+DF=CD+BE.
3.解:(1)等腰直角三角形;
(2)在 FB 上截取 FE = AF,连接AE.
∵AD⊥BM,
∴∠FAE=∠AEF=45°.
∵∠ABO=45°,BF 平分∠ABO,
∴∠ABM=∠OBM=22.5°.
∵∠MAB=90°,
∴∠AMB=67.5°,
∴∠MAF=90°-∠AMB=22.5°,
∴∠MAE=∠MAF+∠FAE=67.5°,∠EAB=90°-∠MAF--∠FAE=22.5°,
∴∠EAB=∠ABM,
∠AMB=∠MAE,
∴ME=AE=EB,
∴AF+MF=EF+MF=ME=AE=BE,
∴BM=2BE,
