45°角用法重难点突破(含解析) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 45°角用法重难点突破(含解析) 2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 494.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
45°角用法重难点突破
45°角用法(一) 构等腰直角
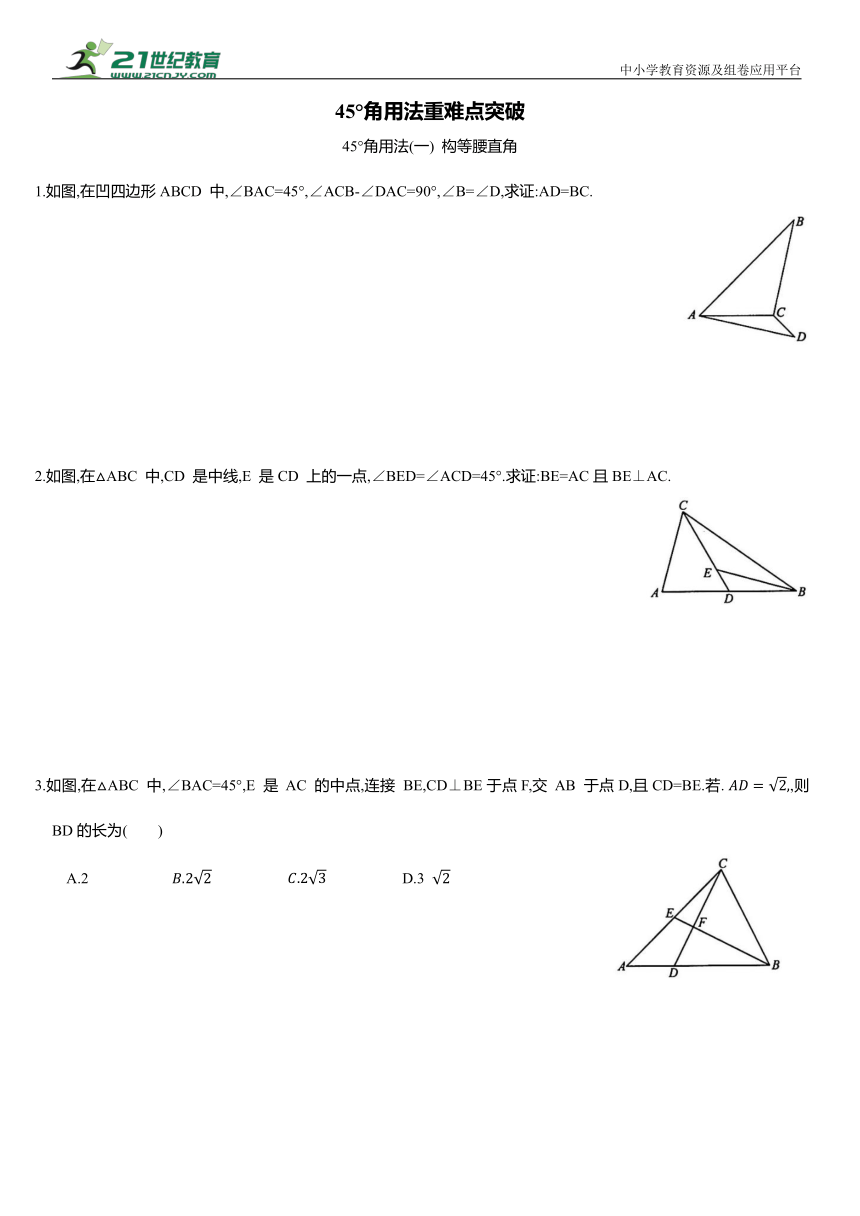
1.如图,在凹四边形ABCD 中,∠BAC=45°,∠ACB-∠DAC=90°,∠B=∠D,求证:AD=BC.
2.如图,在△ABC 中,CD 是中线,E 是CD 上的一点,∠BED=∠ACD=45°.求证:BE=AC且BE⊥AC.
3.如图,在△ABC 中,∠BAC=45°,E 是 AC 的中点,连接 BE,CD⊥BE于点F,交 AB 于点D,且CD=BE.若. ,则 BD的长为( )
A.2 D.3
45°角用法(二) 构模型
类型一 三垂直
1.如图,在 Rt△ABC中,∠ABC=45°,D 是 BC下方一点,AD=AB=AC,连接BD,CD,AE⊥BD 于点E,若AE=8,BD=10,则△BDC 的面积为 .
类型二 夹半角
2.如图,在△ABC中,AC=BC,∠ACB=90°,AD⊥AB 于点A,点E 在AB上,且∠DCE=45°,求证:AD+BE=DE.
类型三 手拉手
3.如图,D 是△ABC 内一点,BD=CD,BD⊥CD,∠BAD=45°,若AB=8,求△ABC 的面积.
45°角用法(三) 巧用45°
类型一 转移45°
1.如图,在 Rt△ABC中,∠ACB=90°,AC=7,BC=5,D,E 分别是边AC,BC 上的点,BE=CD,AE,BD 交于点F,∠AFD=45°,连接DE,则△CDE 的面积为 .
类型二 绝配角
2.如图,在Rt△ABC中,∠ABC=90°,D,E 分别是边BC,AB 上的点,∠ADE=45°,∠ACB=2∠BDE.
(1)求证:AD平分∠BAC;
(2)探究 AE,DC 和AC 之间的数量关系.
3.如图,在Rt△ABC中,∠ACB=90°,E 是边BC 的中点,D 是边AB 上的一点,∠CDE=45°,∠ABC=2∠ACD.
(1)求证:BC=BD;
(2)求证:AB=2AC-AD.
突破31 45°角用法(一)构等腰直角
1.证明:过点 C 作 CE⊥AC 交 AB 于点E,
∴∠ACE=90°.
∵∠BAC=45°,
∴∠AEC=45°,
∴∠BAC=∠AEC,
∴AC=CE.
∵∠ACB =∠ACE+∠BCE =90°+∠BCE,∠ACB-∠DAC=90°,
∴∠ACB-∠DAC=90°+∠BCE—∠DAC=90°,
∴∠BCE=∠DAC.
∵∠B=∠D,
∴△ACD≌△CEB,
∴AD=BC.
2.证明:延长 BE 交 AC 于点 F,过点A 作AH⊥AC 交CD 的延长线于点H.
∵∠BED=∠ACD=45°,
∴△CEF 和△ACH 都为等腰直角三角形,
∴∠EFC=∠CAH,
∴BF∥AH.
∵D是AB的中点,
∴AD=BD,△ADH≌△BDE,
∴AH=BE.
∵AC=AH,
∴AC=BE.
∵AH⊥AC,BE∥AH,
∴BE⊥AC,
∴BE=AC 且BE⊥AC.
3. B 解:过点C 作CN⊥AB 于点 N,连接ED,EN,
∴∠CNA=90°.
∵∠BAC=45°,
∴∠NCA=∠A=45°,
∴AN=CN.
∵E是AC 的中点,
∴∠ANE=∠CNE=45°,
∠CEN=∠AEN=90°,
∴EN=AE=CE,∠CEF+∠FEN=90°.
∵CD⊥BE,
∴∠CFE=90°,
∴∠CEF+∠DCE=90°,
∴∠DCE=∠BEN.
∵CD=EB,
∴△DCE≌△BEN,
∴ED = NB,∠CED =∠ENB =135°,
∠ANE,
∴AD=DE=DN,
∴AD=DN=BN,
突破 32 45°角用法(二) 构模型
1.15 解:过点 C 作CF⊥AE 于点 F.∵AB=AD,AE⊥BD,
∴BE=DE=5.
∵AB=AC,∠BAE=∠ACF,
∴△ABE≌△CAF,得AF=BE=5,
∴EF=AE-AF=3,
=15.
2.证明:延长AB 至点F,使BF=AD,连接CF.
∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
∵AD⊥AB,
∴∠DAE=90°,
∴∠CAD=∠CBF=135°,
∴△CAD≌△CBF(SAS),
∴CD=CF,∠ACD=∠BCF.
∵∠DCE=45°,
∴∠ACD +∠BCE = 90°- 45°=45°,
∴∠BCE+∠BCF=45°,
∴∠DCE=∠FCE=45°.
∵CD=CF,CE=CE,
∴△CDE≌△CFE(SAS),
∴DE=EF,
∴AD+BE=BF+BE=EF=DE.
3.解:过点 D 作 DE⊥AD 交AB 于点E,连接CE.
∵∠BAD=45°,
∴△ADE 为等腰直角三角形,
∴△ABD≌△ECD(SAS),
∴AB=CE=8,
∴∠DAB=∠DEC=∠DEA=45°,
∴∠AEC=90°,CE⊥AB,
=32.
突破 33 45°角用法(三)巧用 45°
1.3 解:过点 D 作 DH∥AE,过点 B作 BH⊥BD 交 DH 于点 H,连接HE,
∴∠BDH=∠AFD=45°,
∴△BDH 为等腰直角三角形.
∵BE=CD,BH=BD,
∴△BHE≌△DBC,
∴HE=BC,
∠BEH=∠BCD=90°,
∴EH∥AD.
证△ADE≌△HED,
∴AD=EH=BC,
∴AD=BC=5,CD=BE=AC-AD=2,CE=BC-BE=3,
∴S△CDE=3.
2.解:(1)设∠BDE=α,则∠ACB=2α.
∵∠ABC=90°,∠ADE=45°,
∴∠BDA=45°+α,
∴∠BAD=90°-∠BDA=45°-α.
∵∠BAC=90°-∠ACB=90°-2α,
∴∠CAD=∠BAD=45°-α,
∴AD 平分∠BAC;
(2)过点 D 作 DF⊥DE 交 AC 于点F,
∴∠ADF=∠ADE=45°.
由(1)得∠CAD=∠BAD,
∴△ADE≌△ADF,
∴AE=AF,
∴∠CDF=90°-∠BDE=90°-α.
∵∠ACB=2α,
∴∠CFD=180°-∠ACB-∠CDF=90°-α,
∴∠CDF=∠CFD,
∴CD=CF,
∴AC=AF+CF=AE+CD.
3.证明:(1)设∠ACD=α,则∠ABC=2α.
∵∠ACB=90°,
∴∠BCD=90°-α,
∴∠BDC=180°-∠ABC-∠BCD=90°-α,
∴BC=BD;
(2)过点 C 作 CF⊥DE 交 AB 于点F.
∵∠CDE=45°,
∴∠DCF=45°,
∴∠ACF=α+45°.
∵∠BAC=90°-2α,
∴∠AFC=α+45°=∠ACF,
∴AF=AC.
∵BC=BD,
∴∠BCF=∠BDE,
∴△BCF≌△BDE,
∴BF=BE.
∵E 是BC 的中点,
∴DF=BF.
∵DF=AF-AD=AC-AD,
∴AB =AD+BD=AD+2DF =AD+2AC-2AD=2AC-AD.
45°角用法重难点突破
45°角用法(一) 构等腰直角
1.如图,在凹四边形ABCD 中,∠BAC=45°,∠ACB-∠DAC=90°,∠B=∠D,求证:AD=BC.
2.如图,在△ABC 中,CD 是中线,E 是CD 上的一点,∠BED=∠ACD=45°.求证:BE=AC且BE⊥AC.
3.如图,在△ABC 中,∠BAC=45°,E 是 AC 的中点,连接 BE,CD⊥BE于点F,交 AB 于点D,且CD=BE.若. ,则 BD的长为( )
A.2 D.3
45°角用法(二) 构模型
类型一 三垂直
1.如图,在 Rt△ABC中,∠ABC=45°,D 是 BC下方一点,AD=AB=AC,连接BD,CD,AE⊥BD 于点E,若AE=8,BD=10,则△BDC 的面积为 .
类型二 夹半角
2.如图,在△ABC中,AC=BC,∠ACB=90°,AD⊥AB 于点A,点E 在AB上,且∠DCE=45°,求证:AD+BE=DE.
类型三 手拉手
3.如图,D 是△ABC 内一点,BD=CD,BD⊥CD,∠BAD=45°,若AB=8,求△ABC 的面积.
45°角用法(三) 巧用45°
类型一 转移45°
1.如图,在 Rt△ABC中,∠ACB=90°,AC=7,BC=5,D,E 分别是边AC,BC 上的点,BE=CD,AE,BD 交于点F,∠AFD=45°,连接DE,则△CDE 的面积为 .
类型二 绝配角
2.如图,在Rt△ABC中,∠ABC=90°,D,E 分别是边BC,AB 上的点,∠ADE=45°,∠ACB=2∠BDE.
(1)求证:AD平分∠BAC;
(2)探究 AE,DC 和AC 之间的数量关系.
3.如图,在Rt△ABC中,∠ACB=90°,E 是边BC 的中点,D 是边AB 上的一点,∠CDE=45°,∠ABC=2∠ACD.
(1)求证:BC=BD;
(2)求证:AB=2AC-AD.
突破31 45°角用法(一)构等腰直角
1.证明:过点 C 作 CE⊥AC 交 AB 于点E,
∴∠ACE=90°.
∵∠BAC=45°,
∴∠AEC=45°,
∴∠BAC=∠AEC,
∴AC=CE.
∵∠ACB =∠ACE+∠BCE =90°+∠BCE,∠ACB-∠DAC=90°,
∴∠ACB-∠DAC=90°+∠BCE—∠DAC=90°,
∴∠BCE=∠DAC.
∵∠B=∠D,
∴△ACD≌△CEB,
∴AD=BC.
2.证明:延长 BE 交 AC 于点 F,过点A 作AH⊥AC 交CD 的延长线于点H.
∵∠BED=∠ACD=45°,
∴△CEF 和△ACH 都为等腰直角三角形,
∴∠EFC=∠CAH,
∴BF∥AH.
∵D是AB的中点,
∴AD=BD,△ADH≌△BDE,
∴AH=BE.
∵AC=AH,
∴AC=BE.
∵AH⊥AC,BE∥AH,
∴BE⊥AC,
∴BE=AC 且BE⊥AC.
3. B 解:过点C 作CN⊥AB 于点 N,连接ED,EN,
∴∠CNA=90°.
∵∠BAC=45°,
∴∠NCA=∠A=45°,
∴AN=CN.
∵E是AC 的中点,
∴∠ANE=∠CNE=45°,
∠CEN=∠AEN=90°,
∴EN=AE=CE,∠CEF+∠FEN=90°.
∵CD⊥BE,
∴∠CFE=90°,
∴∠CEF+∠DCE=90°,
∴∠DCE=∠BEN.
∵CD=EB,
∴△DCE≌△BEN,
∴ED = NB,∠CED =∠ENB =135°,
∠ANE,
∴AD=DE=DN,
∴AD=DN=BN,
突破 32 45°角用法(二) 构模型
1.15 解:过点 C 作CF⊥AE 于点 F.∵AB=AD,AE⊥BD,
∴BE=DE=5.
∵AB=AC,∠BAE=∠ACF,
∴△ABE≌△CAF,得AF=BE=5,
∴EF=AE-AF=3,
=15.
2.证明:延长AB 至点F,使BF=AD,连接CF.
∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°.
∵AD⊥AB,
∴∠DAE=90°,
∴∠CAD=∠CBF=135°,
∴△CAD≌△CBF(SAS),
∴CD=CF,∠ACD=∠BCF.
∵∠DCE=45°,
∴∠ACD +∠BCE = 90°- 45°=45°,
∴∠BCE+∠BCF=45°,
∴∠DCE=∠FCE=45°.
∵CD=CF,CE=CE,
∴△CDE≌△CFE(SAS),
∴DE=EF,
∴AD+BE=BF+BE=EF=DE.
3.解:过点 D 作 DE⊥AD 交AB 于点E,连接CE.
∵∠BAD=45°,
∴△ADE 为等腰直角三角形,
∴△ABD≌△ECD(SAS),
∴AB=CE=8,
∴∠DAB=∠DEC=∠DEA=45°,
∴∠AEC=90°,CE⊥AB,
=32.
突破 33 45°角用法(三)巧用 45°
1.3 解:过点 D 作 DH∥AE,过点 B作 BH⊥BD 交 DH 于点 H,连接HE,
∴∠BDH=∠AFD=45°,
∴△BDH 为等腰直角三角形.
∵BE=CD,BH=BD,
∴△BHE≌△DBC,
∴HE=BC,
∠BEH=∠BCD=90°,
∴EH∥AD.
证△ADE≌△HED,
∴AD=EH=BC,
∴AD=BC=5,CD=BE=AC-AD=2,CE=BC-BE=3,
∴S△CDE=3.
2.解:(1)设∠BDE=α,则∠ACB=2α.
∵∠ABC=90°,∠ADE=45°,
∴∠BDA=45°+α,
∴∠BAD=90°-∠BDA=45°-α.
∵∠BAC=90°-∠ACB=90°-2α,
∴∠CAD=∠BAD=45°-α,
∴AD 平分∠BAC;
(2)过点 D 作 DF⊥DE 交 AC 于点F,
∴∠ADF=∠ADE=45°.
由(1)得∠CAD=∠BAD,
∴△ADE≌△ADF,
∴AE=AF,
∴∠CDF=90°-∠BDE=90°-α.
∵∠ACB=2α,
∴∠CFD=180°-∠ACB-∠CDF=90°-α,
∴∠CDF=∠CFD,
∴CD=CF,
∴AC=AF+CF=AE+CD.
3.证明:(1)设∠ACD=α,则∠ABC=2α.
∵∠ACB=90°,
∴∠BCD=90°-α,
∴∠BDC=180°-∠ABC-∠BCD=90°-α,
∴BC=BD;
(2)过点 C 作 CF⊥DE 交 AB 于点F.
∵∠CDE=45°,
∴∠DCF=45°,
∴∠ACF=α+45°.
∵∠BAC=90°-2α,
∴∠AFC=α+45°=∠ACF,
∴AF=AC.
∵BC=BD,
∴∠BCF=∠BDE,
∴△BCF≌△BDE,
∴BF=BE.
∵E 是BC 的中点,
∴DF=BF.
∵DF=AF-AD=AC-AD,
∴AB =AD+BD=AD+2DF =AD+2AC-2AD=2AC-AD.
