全等三角形专项突破--- 找全等2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 全等三角形专项突破--- 找全等2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 13:26:53 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
突破3 找全等(一) SSS
类型一 知三边,先证全等
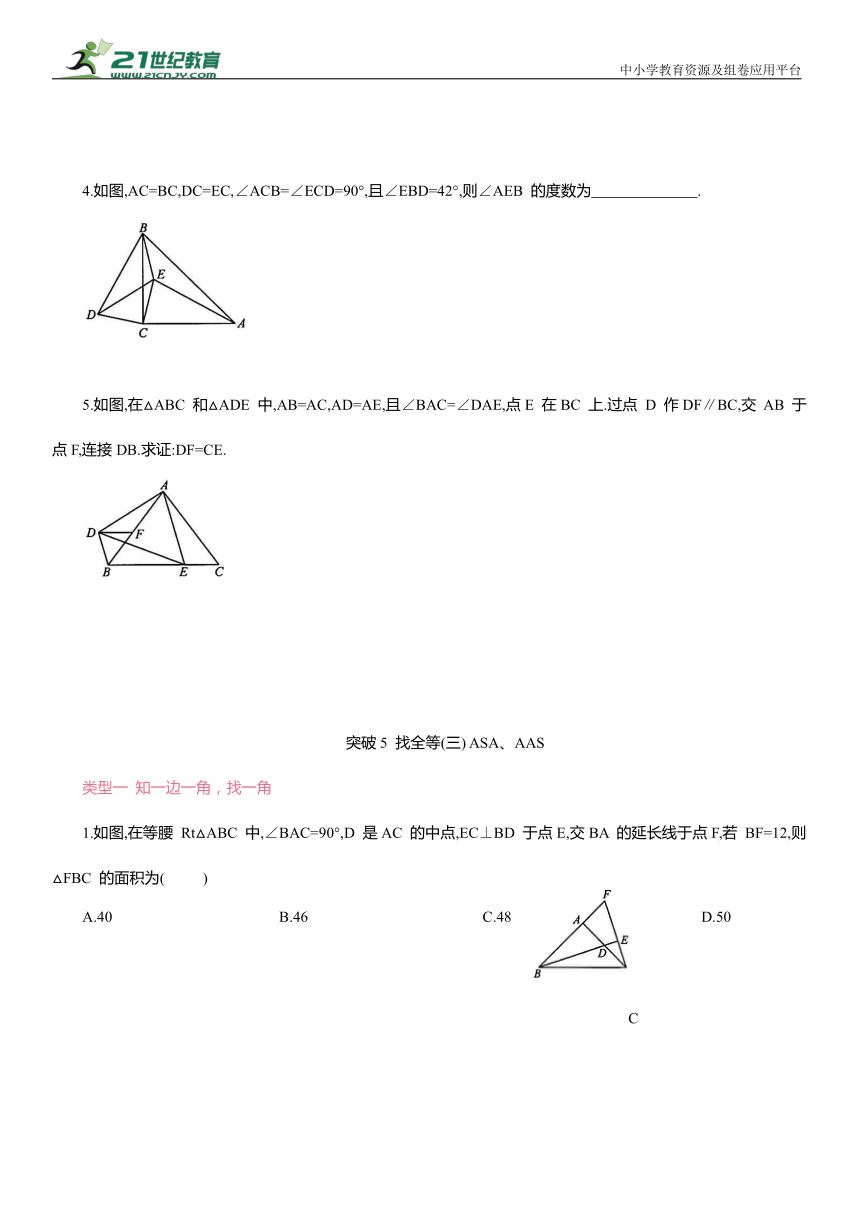
1.如图,在△ABC 中,∠A :∠ABC:∠ACB=3:5 :10,且MN=AB,MC=AC,CN=CB,则∠N 的度数为 .
2.如图,在△ABC中,点D,F 分别在边BC,AC上,若 BC=ED,AC=CD,AB=CE,且 ,则下列角中,大小为m 的是( )
A.∠CDF B.∠ABC C.∠CFD D.∠CFE
3.如图,在△ABC 和△BDE 中,点C 在边BD 上,边AC 交边BE 于点F.若AC=BD,AB=ED,BC=BE,则∠ACB 等于( )
A.∠EDB B.∠BED C.2∠ABF
类型二 知两边,找第三边
4.如图,A,B,C三点共线,BF 与CE交于点D,
(1)求证:
(2)连接EF,求证:
C
突破4 找全等(二) SAS
类型一 隐边
1.如图,AD+BC=AB,BE=CA,∠DBE=∠C=62°,∠BDE=75°,则∠AFD 的度数为( )
A.30° B.32° C.33° D.35°
2.如图,D,E 在△ABC 的边AB上,且∠ADC=∠ACB.若∠BAC 的平分线AF交CD于点F,BE+AC=AB,求证:EF∥BC.
C
类型二 隐角
3.如图,OA=OB,OC=OD,∠AOB=∠COD=α,AC,BD 交于点M,则∠AMD 的度数为( )
A.α C.180°—α
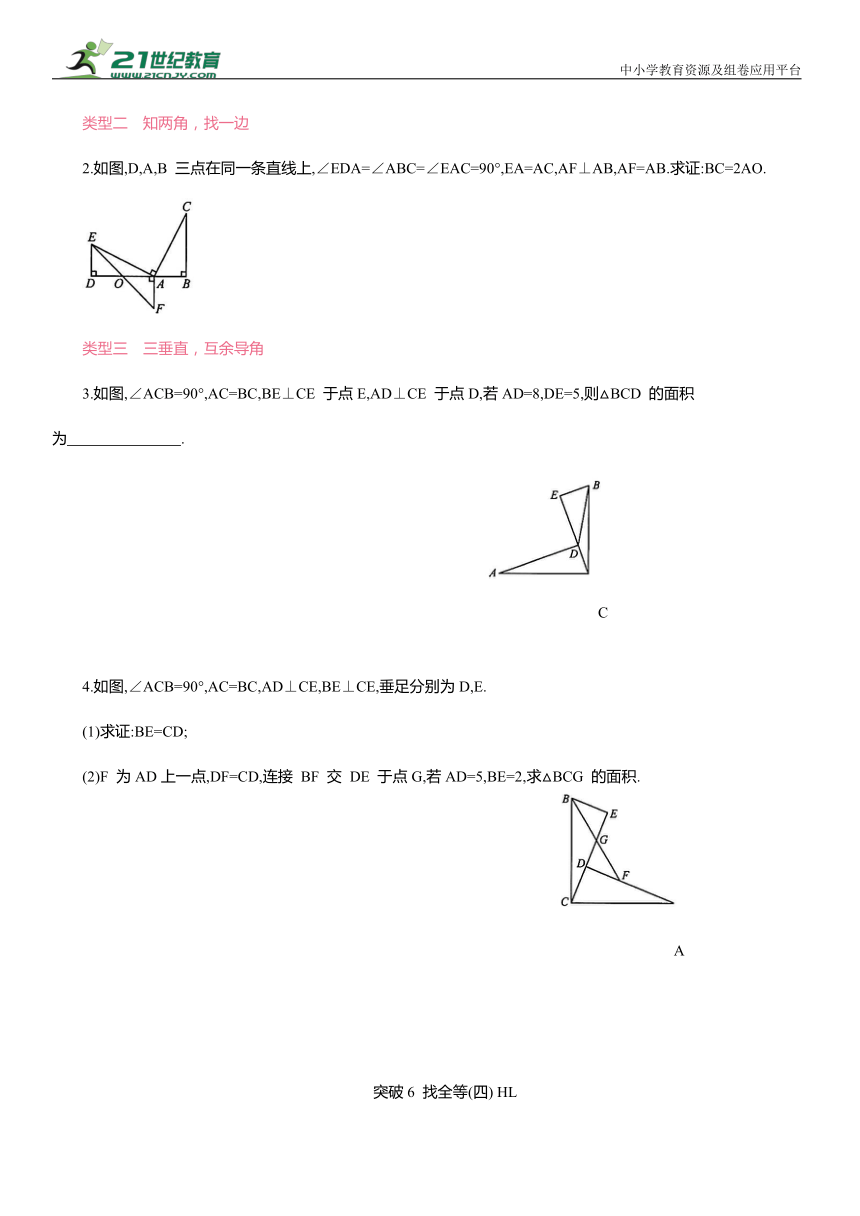
4.如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=42°,则∠AEB 的度数为 .
5.如图,在△ABC 和△ADE 中,AB=AC,AD=AE,且∠BAC=∠DAE,点E 在BC 上.过点 D 作DF∥BC,交 AB 于点F,连接DB.求证:DF=CE.
突破5 找全等(三) ASA、AAS
类型一 知一边一角,找一角
1.如图,在等腰 Rt△ABC 中,∠BAC=90°,D 是AC 的中点,EC⊥BD 于点E,交BA 的延长线于点F,若 BF=12,则△FBC 的面积为( )
A.40 B.46 C.48 D.50
C
类型二 知两角,找一边
2.如图,D,A,B 三点在同一条直线上,∠EDA=∠ABC=∠EAC=90°,EA=AC,AF⊥AB,AF=AB.求证:BC=2AO.
类型三 三垂直,互余导角
3.如图,∠ACB=90°,AC=BC,BE⊥CE 于点E,AD⊥CE 于点D,若AD=8,DE=5,则△BCD 的面积为 .
C
4.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:BE=CD;
(2)F 为AD上一点,DF=CD,连接 BF 交 DE 于点G,若AD=5,BE=2,求△BCG 的面积.
A
突破6 找全等(四) HL
类型一 双垂直,知两边,联想HL
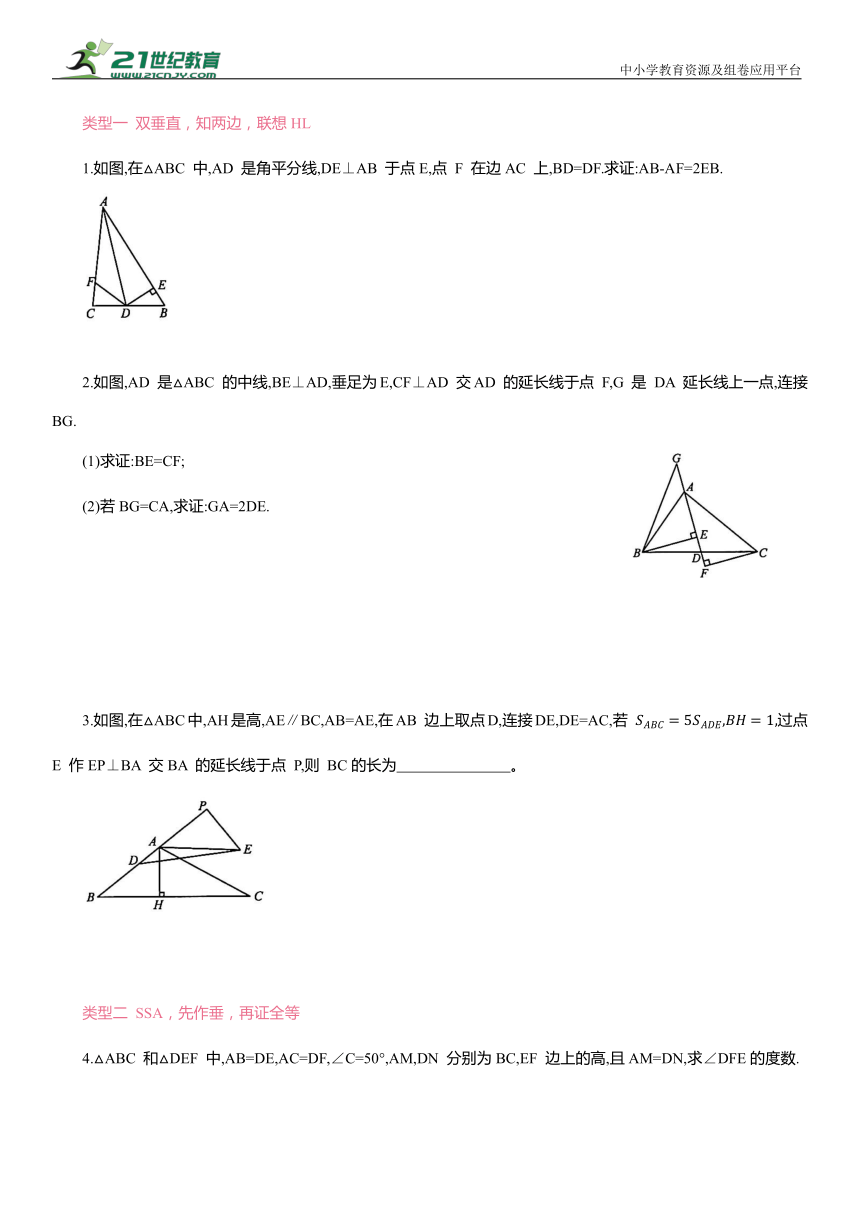
1.如图,在△ABC 中,AD 是角平分线,DE⊥AB 于点E,点 F 在边AC 上,BD=DF.求证:AB-AF=2EB.
2.如图,AD 是△ABC 的中线,BE⊥AD,垂足为E,CF⊥AD 交AD 的延长线于点 F,G 是 DA 延长线上一点,连接BG.
(1)求证:BE=CF;
(2)若BG=CA,求证:GA=2DE.
3.如图,在△ABC中,AH是高,AE∥BC,AB=AE,在AB 边上取点D,连接DE,DE=AC,若 过点 E 作EP⊥BA 交BA 的延长线于点 P,则 BC的长为 。
类型二 SSA,先作垂,再证全等
4.△ABC 和△DEF 中,AB=DE,AC=DF,∠C=50°,AM,DN 分别为BC,EF 边上的高,且AM=DN,求∠DFE的度数.
突破7 找全等(五) 等线段代换证和差
类型一 代换一条线段
1.如图,D 为BC 上一点,AB=AC,AD=AE,∠BAC=∠DAE.求证:BC=CD+CE.
类型二 代换两条线段
2.如图,在△ABC中,∠BAC=90°,AB=AC,直线DE 经过点A,BD⊥DE,垂足为D,CE⊥DE,垂足为E.
(1)如图1,求证:DE=CE+BD;
(2)如图2,求证:DE=CE---BD.
3.如图,AB⊥CD,且AB=CD,E,F 是AD上两点,CE⊥AD,BF⊥AD.若CE=12,BF=9,EF=6,则AD的长为 .
类型三 代换多条线段
4.如图,在 Rt△ABC 中,∠C=90°,∠ABC和∠BAC 的平分线相交于点 O,OD⊥OA 交AC 于点D,OE⊥OB 交BC 于点E,若 BC=4,AC=3,AB=5,求△CDE 的周长.
突破8 找全等(六) 全等计数
类型一 非网格图
1.如图,AB∥CD,AC∥DB,AD 与BC 交于点O,AE⊥BC 于点E,DF⊥BC 于点F,图中全等的三角形共有( )
A.5 对 B.6 对 C.7对 D.8对
2.如图1,已知AB=AC,D 为∠BAC 的角平分线上一点,连接BD,CD;如图2,已知AB=AC,D,E 为∠BAC 的角平分线上两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D,E,F 为∠BAC 的角平分线上三点,连接 BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中全等三角形的对数是( )
A. n
B.2n—1
D.3(n+1)
类型二 网格图,知全等,两定点
3.在正方形方格纸中,每个小正方形的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点 D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC 全等,这样的格点三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
类型三 网格图,知全等,共一边
4.在如图所示的6×6 网格中,△ABC 是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且与△ABC 全等(不含△ABC)的所有格点三角形的个数是( )
A.3个 B.4 个 C.6个 D.7 个
5.在如图所示3×3的正方形网格中,△ABC 的顶点都在小正方形的顶点上,像△ABC 这样顶点均在格点上的三角形叫格点三角形,在图中画与△ABC 有一条公共边且全等的格点三角形,这样的格点三角形最多可以画( )
A.1个 B.2 个 C.3个 D.4个
类型四 网格图,知全等,两点变
6.如图所示,在5×4的长方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC 为格点三角形,以C 为顶点画格点三角形与△ABC 全等(不包括△ABC),则画出的三角形的个数为( )
A.8个 B.9个 C.10个 D.11个
类型五 网格图,知全等,三点变
7.在如图所示3×3的小正方形组成的网格中,△ABC 的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形,图中能画出与△ABC 全等的格点三角形的个数是( )
A.3个 B.4个 C.7个 D.8个
8.如图,在一个4×4 的正方形网格中,△ABC 为格点三角形(三角形的三个顶点都在网格格点上的三角形),在所给的网格中,与△ABC 全等的格点三角形(△ABC 除外)共有( )
A.35 个 B.31个 C.27个 D.15 个
9.如图,在4×4的正方形网格中,△ABC 的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在图中与△ABC 全等(不含△ABC)的格点三角形一共有 个.
突破9 找全等(七) 动点问题
类型一 单动点,知速度,用全等求时间
1.如图,在Rt△ABC 中,∠ACB=90°,BC=7 cm,AC=24 cm,CD 为AB 边上的高,直线CD 上一点F 满足CF=AB,点E 从点B 出发在直线BC 上以3cm/s的速度移动.设运动时间为t秒,当t= 秒时,能使△ABC≌△CFE.
类型二 知速度,用全等,分类讨论求时间
2.如图,在长方形ABCD 中,AB=4,AD=6.延长BC 到点E,使 CE=2,连接DE,动点 P 从点B 出发,以每秒2个单位的速度沿 BC一CD—DA 向终点A 运动.设点 P 的运动时间为t秒,当t的值为 秒时,△ABP 和△DCE 全等.
3.如图,点 C 在线段 BD 上,AB⊥BD 于点 B,ED⊥BD 于点 D.∠ACE=90°,且AC=5 cm,CE=6 cm,点 P 以 2cm/s的速度沿A→C→E 向终点E 运动,同时点 Q 以3c m/s的速度从 E 开始,在线段 EC 上往返运动(即沿E→C→E→C→…运动),当点 P 到达终点时,P,Q 同时停止运动.过点 P,Q分别作BD 的垂线,垂足为M,N.设运动时间为t s,当以 P,C,M 为顶点的三角形与△QCN 全等时,t 的值为( )
A.1 或 3 B.1 或 C.1 或 或 D.1 或 或5
类型三 知时间,用全等,分类讨论求速度
4.如图,AB=7 cm,AC=5cm ,∠CAB=∠DBA,点 P 在线段AB 上以2 cm/s的速度由点 A 向点B 运动,同时点Q 在射线BD 上以x cm/s的速度由点B 向点D 运动,它们运动的时间为t(s)(当点 P 运动结束时,点Q运动随之停止).问:当x 为何值时,△ACP 与△BPQ全等
5.如图,在四边形ABCD 中,∠DAB=∠ABC,AB=5cm,AD=BC=3cm,点E 在线段AB 上以1cm/s的速度由点A 向点B 运动,同时,点 F 在线段BC 上由点B 向点C运动.设运动时间为t(s),当△ADE 与以B,E,F为顶点的三角形全等时,则点 F 的运动速度为 cm/s.
类型四 知速度比,用全等,求长度
6.如图,∠A=∠B=90°,AB=60,E,F 分别为线段AB 和射线BD 上的点,若点 E从点 B 出发向点 A 运动,同时点 F 从点 B 出发向点 D 运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC 上取一点G,使△AEG 与△BEF 全等,则AG 的长为 .
突破 3 找全等(一) SSS
1.50° 解:∵在△ABC 中,∠A :∠ABC:∠ACB=3:5: 10,且∠A+∠ABC+∠ACB=180°,∴∠A=30°,∠BCA=100°,∠ABC=50°.
∵MN=AB,MC=AC,CN=CB,
∴△MNC≌△ABC(SSS),
∴∠N=∠ABC=50°.
2. A 解:∵BC=ED,AC=CD,AB=CE,
∴△ABC≌△CED(SSS),
∴∠EDC=∠BCA,
∠ABC=∠DEC,
∠FDC=∠FCD,
∴∠ACE+∠ABC=180°-2m,
∵∠DFC=∠DEC+∠ACE,
∵∠DFC + ∠FDC + ∠FCD =180°,
∴∠FDC=m.故选 A.
3. D 解:在△ABC 和△DEB 中,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE.
∵∠AFB是△BFC 的外角,
∴ ∠ACB + ∠DBE = ∠AFB, 故选 D.
4.证明:(1)由题意,
得 AC=CB+BA=8,
∴AC=BF.
∵AC=BF,CE=CF,AE=BC,
∴△AEC≌△BCF(SSS);
(2)∵△AEC≌△BCF,
∴S△AEC=S△BCF,
∴S四边形ACFE — S△AEC =S四边形ACFE —S△BCF,
突破 4 找全等(二) SAS
1. B 解:∵AD+BC=AB,AD+BD=AB,
∴BD=BC.
∵BE=CA,∠DBE=∠C,
∴△BDE≌△CBA(SAS),
∴∠BDE=∠CBA=75°.
∵∠C=62°,
∴∠AFD=∠BDE--∠A=75°- 故选 B.
2.证明:∵∠ACD+∠DCB=∠ACB,∠ABC+∠DCB=∠ADC,∠ADC=∠ACB,
∴∠ACD=∠ABC.
∵AF平分∠EAC,
∴∠EAF=∠CAF.
∵AB=AE+BE,AB=BE+AC,
∴AE=AC.
在△AEF 和△ACF 中,
∴△AEF≌△ACF(SAS),
∴∠AEF=∠ACF.
∵∠ACD=∠ABC,
∴∠ABC=∠AEF,
∴EF∥BC.
3. C 解:∵∠AOB=∠COD=α,∴∠AOB + ∠BOC = ∠COD +∠BOC,
∴∠AOC=∠BOD,
∴△AOC≌△BOD(SAS),
∴∠A=∠B,
∴∠AOB=∠AMB=α.
α.故选 C.
4.132° 解:∵∠ACB=∠ECD=90°,∴∠BCD=∠ACE.
在△BDC 和△AEC 中,
∴△BDC≌△AEC(SAS),
∴∠DBC=∠EAC.
∵∠EBD=∠DBC+∠EBC=42°,
∴∠EAC+∠EBC=42°,
48°,
∴∠AEB = 180° (∠ABE + .故答案为 132°.
5.证明:∵∠BAC=∠DAE,
∴ ∠BAC - ∠BAE = ∠DAE -∠BAE,
∴∠BAD=∠EAC.
又∵AD=AE,AB=AC,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠DBA=∠C.
∵AB=AC,
∴∠C=∠ABC.
∵DF∥BC,
∴∠DFB=∠ABC=∠C=∠DBA.即∠DFB=∠DBF,
∴DF=DB,
∴DF=CE.
突破 5 找全等(三) ASA、AAS
1. C 解:∵CE⊥BD,
∴∠BEF=90°.
∵∠BAC=90°,
∴∠CAF=90°,
∴∠FAC=∠BAD=90°.
∵∠ABD+∠F=90°,∠ACF+∠F=90°,
∴∠ABD=∠ACF.
在△ABD 和△ACF 中,
∴△ABD≌△ACF(ASA),
∴AD=AF.
∵AB=AC,D 为AC中点,
∴AB=AC=2AD=2AF.
∵BF=AB+AF=12,
∴3AF=12,
∴AF=4,
∴AB=AC=2AF=8,
∴△FBC 的面积是 故选 C.
2.证明:∵∠EDA=∠ABC=∠EAC=90°,
∴∠EAD + ∠CAB = ∠ACB +∠CAB=90°,
∴∠EAD=∠ACB.
∵EA=AC,
∴△ABC≌△EDA(AAS),
∴AF=AB=ED,AD=BC.
∵AF⊥AB,
∴∠EDA=∠FAD=90°.
∵∠EOD=∠FOA,
∴△AOF≌△DOE(AAS),
∴OA=OD,
∴AD=2OA,
∴BC=2OA.
3. 解:∵∠ACB=90°,
∴∠BCE+∠ECA=90°,
∵AD⊥CE,
∴∠CAD+∠ECA=90°,
∴∠CAD=∠BCE.
在△ACD 与△CBE 中,
∴△ACD≌△CBE(AAS),
∴BE=CD,CE=AD=8,
∴BE=CD=CE--DE=8-5=3,
故答案为
4.解:(1)∵∠ACB=90°,BE⊥CE,∴∠ECB+∠ACD=90°,∠ECB+∠CBE=90°,
∴∠ACD=∠CBE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
∵AC=BC,
∴△ACD≌△CBE(AAS),
∴CD=BE;
(2)∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∵FD=CD,
∴FD=BE,
∵AD⊥CE,BE⊥CE,
∴∠BEG=∠FDG=90°,
∵∠FGD=∠BGE,
∴△FDG≌△BEG(AAS),
∴EG=DG,
∵AD=5,BE=2,
突破 6 找全等(四) HL
1.证明:过点 D 作 DG⊥AC 于点 G.
∵AD 是角平分线,DE⊥AB 于点E,DG⊥AC,
∴DG=DE,
∴Rt△FGD≌Rt△BED(HL),Rt△AGD≌Rt△AED(HL),
∴FG=BE,AG=AE,
∴AB-AF=AB-(AG--FG)=AB--(AE--BE)=AB-AE+BE=2BE.
2.证明:(1)∵AD是△ABC的中线,
∴BD=CD.
∵BE⊥AD,CF⊥AD,
∴∠BED=∠F,
∴△BED≌△CFD(AAS),
∴BE=CF;
(2)在 Rt△BGE 和 Rt△CAF 中,
∴Rt△BGE≌Rt△CAF(HL),
∴GE=AF,
∴AG=EF.
∵△BED≌△CFD,
∴DE=DF,
∴GA=2DE.
3. 解:∵EP⊥AB,AH是高,
∴∠P=∠AHB=90°.
∵AE∥BC,
∴∠EAP=∠CBA.
在△AEP 和△BAH 中,
∴△AEP≌△BAH(AAS),
∴PE=AH,AP=BH=1.
在 Rt△DEP 和 Rt△CAH 中,
∴Rt△DEP≌Rt△CAH(HL),
∴CH=DP.设 AD=x,则 CH=DP=x+1.
4.解:如图1所示,
∵AM,DN 分别为 BC,EF 边上的高,
∴△ACM 和△DFN 均为直角三角形.
∵在 Rt△ACM 和 Rt△DFN 中,
∴Rt△ACM≌Rt△DFN(HL),
∴∠DFE=∠ACB=50°;如图 2 所示,
∵AM,DN分别为 BC,EF 边上的高,
∴△ACM 和△DFN 均为直角三角形,
∴Rt△ACM≌Rt△DFN(HL),
∴∠DFN=∠ACB=50°,
∴∠DFE=130°.
综上所述,∠DFE 的度数为 50°或130°.
突破 7 找全等(五)
等线段代换证和差
1.证明:由条件可得△ACE≌△ABD(SAS),
∴BD=CE,
∴BC=CD+BD=CD+CE.
2.证明:(1)易得 △ABD ≌△CAE(AAS),
∴AD=CE,AE=BD,
∴DE=AD+AE=CE+BD;
(2)同(1)AD=CE,AE=BD,
∴DE=AD-AE=CE--BD.
3.15 解:设AB 分别交CE,CD 于点G,H,则∠AGE=∠CGH.
∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AHC = ∠AEC = ∠CED =
∴∠A = 90°— ∠AGE = 90°—∠CGH=∠C.
∵AB=CD,
∴△ABF≌△CDE(AAS),
∴AF=CE=12,BF=DE=9,EF=6,
∴DF=DE--EF=9-6=3,
∴AD=AF+DF=12+3=15.
4.解:延长 DO 交 AB 于点 M,延长EO 交AB 于点 N.
∵BO 是∠ABC 的平分线,
∴∠OBE=∠OBN.
∵OE⊥OB,
∴∠BOE=∠BON=90°.
∴△BOE≌△BON(ASA).
同理可得,△AOD≌△AOM,
∴OE=ON,OD=OM,BE=BN,AD=AM.
∴△EOD≌△NOM(SAS),
∴DE=MN.
∴CE+CD+DE=BC-BE+AC-AD+MN=BC-(BM+MN)+AC--(AN+MN)+MN = BC-BM--MN+AC-AN=BC+AC-AB=4+3-5=2.
突破8 找全等(六) 全等计数
1. C 解:△ACE≌△DBF,△ACO≌△DBO,△ACB≌△DBC,△AEO≌ △DFO, △AEB ≌ △DFC,△ABO ≌ △DCO, △ABD ≌△DCA,共7 对.故选 C.
2. C 解:图1 中有 1 对三角形全等;图2 中有 3 对三角形全等;图3 中有6对三角形全等;由此发现,第n 个图 形 中 全 等 三 角 形 的 对 数 是 故选 C.
3. B 解:如图,共4个.故选 B.
4. D 解:以 AB 为公共边的有1个,以 AC 为公共边的有 3 个,以 BC 为公共边的有3个,共计7个.故选 D.
5. D 解:以AB 为公共边的三角形有3个,以BC 为公共边的三角形有0个,以AC 为公共边的三角形有 1个,共3+0+1=4个.故选 D.
6. B 解:共有 9 种情况.故选 B.
7. C 解:共2×4-1=7个.故选 C.
8. B 解:在每个 3×3 的网格中,与△ABC全等的格点三角形一共有 8个,
而网格中共有3×3的网格4个,∴共还有8×4-1=31(个).故选 B.
9.31 解:在 3 × 3 的 网 格中,与△ABC 全等的格点三角形(不含△ABC)一共有7个,
而网格中共有3×3的网格 4个,∴共有7×4+3=31个.
故答案为31.
突破9 找全等(七) 动点问题1. 或 解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=∠A+∠ACD=90°,
∴∠A=∠BCD.
∵∠ECF=∠BCD,
∴∠ECF=∠A.当 F 在C 上方时,
∵AB=CF,∠A=∠ECF,
∴当CE=AC=24 cm时,△ABC≌△CFE.
∵BE=BC+CE=7+24=31( cm),
当 F 在C下方时,
∵CF'=AB,∠BCD=∠A,
∴当 时,△ABC≌△CFE.
∴当 或 时,能使△ABC≌△CFE.故答案为 或
2.1 或 7 解:∵AB=CD,若∠ABP
=∠DCE=90°,BP=CE=2,
∴△ABP≌△DCE.
∵BP=2t=2,
∴t=1;
∵AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,
∴△BAP≌△DCE.
∵AP=16-2t=2,解得t=7.
综上,当t 的值为 1 或 7 秒时,△ABP 和△DCE 全等.故答案为1或 7.
3. C 解:当点 P 在AC 上时,
∵以 P,C,M 为顶点的三角形与△QCN 全等,
∴PC=CQ,
∴5-2t=6-3t,
∴t=1;
当点 P 在 AC 上,点Q 第一次从点C 返回时,
∵以P,C,M为
顶点的三角形与△QCN 全等,
∴PC=CQ,
∴5-2t=3t-6,
当点 P 在 CE 上,点 Q 第一次从 E点返回时,
∵以 P,C,M 为顶点的三角形与△QCN 全等,
∴PC=CQ,
∴2t-5=18-3t,
综上所述,t的值为 1 或 或 .故选 C.
4.解:①若△ACP≌△BPQ,则 AC=BP,AP=BQ,可得 解得
②若△ACP≌△BQP,则AC=BQ,AP=BP,可得 解得 综上所述,当△ACP 与△BPQ全等时,x的值为2 或
5.1或1.2 解:设点 F 的运动速度为x cm/s,则AE=t cm,
BE=(5-t) cm,BF= xt cm,
∵∠DAB=∠ABC,
∴当AD=BE,AE=BF时,
根据“SAS”判断△ADE≌△BEF,
即5-t=3,t= xt,解得t=2,x=1;
当 AD = BF,AE = BE 时, 根 据
“SAS”判断△ADE≌△BFE,
即 xt=3,t=5-t,
解得t=2.5,x=1.2.
综上所述,点 F 的运动速度为 1 cm/s或1.2cm/s.
6.18或70 解:由题意知,BE : BF=3:7,设BE=3t,则 BF=7t,AE=60-3t;
①当△AEG≌△BFE时,AE=BF,∴60-3t=7t,t=6,
∴AG=BE=3t=18;
②当△AEG≌△BEF时,AE=BE,60-3t=3t,t=10,AG=BF=7t=70.
故 AG=18或 70.
突破3 找全等(一) SSS
类型一 知三边,先证全等
1.如图,在△ABC 中,∠A :∠ABC:∠ACB=3:5 :10,且MN=AB,MC=AC,CN=CB,则∠N 的度数为 .
2.如图,在△ABC中,点D,F 分别在边BC,AC上,若 BC=ED,AC=CD,AB=CE,且 ,则下列角中,大小为m 的是( )
A.∠CDF B.∠ABC C.∠CFD D.∠CFE
3.如图,在△ABC 和△BDE 中,点C 在边BD 上,边AC 交边BE 于点F.若AC=BD,AB=ED,BC=BE,则∠ACB 等于( )
A.∠EDB B.∠BED C.2∠ABF
类型二 知两边,找第三边
4.如图,A,B,C三点共线,BF 与CE交于点D,
(1)求证:
(2)连接EF,求证:
C
突破4 找全等(二) SAS
类型一 隐边
1.如图,AD+BC=AB,BE=CA,∠DBE=∠C=62°,∠BDE=75°,则∠AFD 的度数为( )
A.30° B.32° C.33° D.35°
2.如图,D,E 在△ABC 的边AB上,且∠ADC=∠ACB.若∠BAC 的平分线AF交CD于点F,BE+AC=AB,求证:EF∥BC.
C
类型二 隐角
3.如图,OA=OB,OC=OD,∠AOB=∠COD=α,AC,BD 交于点M,则∠AMD 的度数为( )
A.α C.180°—α
4.如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=42°,则∠AEB 的度数为 .
5.如图,在△ABC 和△ADE 中,AB=AC,AD=AE,且∠BAC=∠DAE,点E 在BC 上.过点 D 作DF∥BC,交 AB 于点F,连接DB.求证:DF=CE.
突破5 找全等(三) ASA、AAS
类型一 知一边一角,找一角
1.如图,在等腰 Rt△ABC 中,∠BAC=90°,D 是AC 的中点,EC⊥BD 于点E,交BA 的延长线于点F,若 BF=12,则△FBC 的面积为( )
A.40 B.46 C.48 D.50
C
类型二 知两角,找一边
2.如图,D,A,B 三点在同一条直线上,∠EDA=∠ABC=∠EAC=90°,EA=AC,AF⊥AB,AF=AB.求证:BC=2AO.
类型三 三垂直,互余导角
3.如图,∠ACB=90°,AC=BC,BE⊥CE 于点E,AD⊥CE 于点D,若AD=8,DE=5,则△BCD 的面积为 .
C
4.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:BE=CD;
(2)F 为AD上一点,DF=CD,连接 BF 交 DE 于点G,若AD=5,BE=2,求△BCG 的面积.
A
突破6 找全等(四) HL
类型一 双垂直,知两边,联想HL
1.如图,在△ABC 中,AD 是角平分线,DE⊥AB 于点E,点 F 在边AC 上,BD=DF.求证:AB-AF=2EB.
2.如图,AD 是△ABC 的中线,BE⊥AD,垂足为E,CF⊥AD 交AD 的延长线于点 F,G 是 DA 延长线上一点,连接BG.
(1)求证:BE=CF;
(2)若BG=CA,求证:GA=2DE.
3.如图,在△ABC中,AH是高,AE∥BC,AB=AE,在AB 边上取点D,连接DE,DE=AC,若 过点 E 作EP⊥BA 交BA 的延长线于点 P,则 BC的长为 。
类型二 SSA,先作垂,再证全等
4.△ABC 和△DEF 中,AB=DE,AC=DF,∠C=50°,AM,DN 分别为BC,EF 边上的高,且AM=DN,求∠DFE的度数.
突破7 找全等(五) 等线段代换证和差
类型一 代换一条线段
1.如图,D 为BC 上一点,AB=AC,AD=AE,∠BAC=∠DAE.求证:BC=CD+CE.
类型二 代换两条线段
2.如图,在△ABC中,∠BAC=90°,AB=AC,直线DE 经过点A,BD⊥DE,垂足为D,CE⊥DE,垂足为E.
(1)如图1,求证:DE=CE+BD;
(2)如图2,求证:DE=CE---BD.
3.如图,AB⊥CD,且AB=CD,E,F 是AD上两点,CE⊥AD,BF⊥AD.若CE=12,BF=9,EF=6,则AD的长为 .
类型三 代换多条线段
4.如图,在 Rt△ABC 中,∠C=90°,∠ABC和∠BAC 的平分线相交于点 O,OD⊥OA 交AC 于点D,OE⊥OB 交BC 于点E,若 BC=4,AC=3,AB=5,求△CDE 的周长.
突破8 找全等(六) 全等计数
类型一 非网格图
1.如图,AB∥CD,AC∥DB,AD 与BC 交于点O,AE⊥BC 于点E,DF⊥BC 于点F,图中全等的三角形共有( )
A.5 对 B.6 对 C.7对 D.8对
2.如图1,已知AB=AC,D 为∠BAC 的角平分线上一点,连接BD,CD;如图2,已知AB=AC,D,E 为∠BAC 的角平分线上两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D,E,F 为∠BAC 的角平分线上三点,连接 BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中全等三角形的对数是( )
A. n
B.2n—1
D.3(n+1)
类型二 网格图,知全等,两定点
3.在正方形方格纸中,每个小正方形的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点 D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC 全等,这样的格点三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
类型三 网格图,知全等,共一边
4.在如图所示的6×6 网格中,△ABC 是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且与△ABC 全等(不含△ABC)的所有格点三角形的个数是( )
A.3个 B.4 个 C.6个 D.7 个
5.在如图所示3×3的正方形网格中,△ABC 的顶点都在小正方形的顶点上,像△ABC 这样顶点均在格点上的三角形叫格点三角形,在图中画与△ABC 有一条公共边且全等的格点三角形,这样的格点三角形最多可以画( )
A.1个 B.2 个 C.3个 D.4个
类型四 网格图,知全等,两点变
6.如图所示,在5×4的长方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC 为格点三角形,以C 为顶点画格点三角形与△ABC 全等(不包括△ABC),则画出的三角形的个数为( )
A.8个 B.9个 C.10个 D.11个
类型五 网格图,知全等,三点变
7.在如图所示3×3的小正方形组成的网格中,△ABC 的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形,图中能画出与△ABC 全等的格点三角形的个数是( )
A.3个 B.4个 C.7个 D.8个
8.如图,在一个4×4 的正方形网格中,△ABC 为格点三角形(三角形的三个顶点都在网格格点上的三角形),在所给的网格中,与△ABC 全等的格点三角形(△ABC 除外)共有( )
A.35 个 B.31个 C.27个 D.15 个
9.如图,在4×4的正方形网格中,△ABC 的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在图中与△ABC 全等(不含△ABC)的格点三角形一共有 个.
突破9 找全等(七) 动点问题
类型一 单动点,知速度,用全等求时间
1.如图,在Rt△ABC 中,∠ACB=90°,BC=7 cm,AC=24 cm,CD 为AB 边上的高,直线CD 上一点F 满足CF=AB,点E 从点B 出发在直线BC 上以3cm/s的速度移动.设运动时间为t秒,当t= 秒时,能使△ABC≌△CFE.
类型二 知速度,用全等,分类讨论求时间
2.如图,在长方形ABCD 中,AB=4,AD=6.延长BC 到点E,使 CE=2,连接DE,动点 P 从点B 出发,以每秒2个单位的速度沿 BC一CD—DA 向终点A 运动.设点 P 的运动时间为t秒,当t的值为 秒时,△ABP 和△DCE 全等.
3.如图,点 C 在线段 BD 上,AB⊥BD 于点 B,ED⊥BD 于点 D.∠ACE=90°,且AC=5 cm,CE=6 cm,点 P 以 2cm/s的速度沿A→C→E 向终点E 运动,同时点 Q 以3c m/s的速度从 E 开始,在线段 EC 上往返运动(即沿E→C→E→C→…运动),当点 P 到达终点时,P,Q 同时停止运动.过点 P,Q分别作BD 的垂线,垂足为M,N.设运动时间为t s,当以 P,C,M 为顶点的三角形与△QCN 全等时,t 的值为( )
A.1 或 3 B.1 或 C.1 或 或 D.1 或 或5
类型三 知时间,用全等,分类讨论求速度
4.如图,AB=7 cm,AC=5cm ,∠CAB=∠DBA,点 P 在线段AB 上以2 cm/s的速度由点 A 向点B 运动,同时点Q 在射线BD 上以x cm/s的速度由点B 向点D 运动,它们运动的时间为t(s)(当点 P 运动结束时,点Q运动随之停止).问:当x 为何值时,△ACP 与△BPQ全等
5.如图,在四边形ABCD 中,∠DAB=∠ABC,AB=5cm,AD=BC=3cm,点E 在线段AB 上以1cm/s的速度由点A 向点B 运动,同时,点 F 在线段BC 上由点B 向点C运动.设运动时间为t(s),当△ADE 与以B,E,F为顶点的三角形全等时,则点 F 的运动速度为 cm/s.
类型四 知速度比,用全等,求长度
6.如图,∠A=∠B=90°,AB=60,E,F 分别为线段AB 和射线BD 上的点,若点 E从点 B 出发向点 A 运动,同时点 F 从点 B 出发向点 D 运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC 上取一点G,使△AEG 与△BEF 全等,则AG 的长为 .
突破 3 找全等(一) SSS
1.50° 解:∵在△ABC 中,∠A :∠ABC:∠ACB=3:5: 10,且∠A+∠ABC+∠ACB=180°,∴∠A=30°,∠BCA=100°,∠ABC=50°.
∵MN=AB,MC=AC,CN=CB,
∴△MNC≌△ABC(SSS),
∴∠N=∠ABC=50°.
2. A 解:∵BC=ED,AC=CD,AB=CE,
∴△ABC≌△CED(SSS),
∴∠EDC=∠BCA,
∠ABC=∠DEC,
∠FDC=∠FCD,
∴∠ACE+∠ABC=180°-2m,
∵∠DFC=∠DEC+∠ACE,
∵∠DFC + ∠FDC + ∠FCD =180°,
∴∠FDC=m.故选 A.
3. D 解:在△ABC 和△DEB 中,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠DBE.
∵∠AFB是△BFC 的外角,
∴ ∠ACB + ∠DBE = ∠AFB, 故选 D.
4.证明:(1)由题意,
得 AC=CB+BA=8,
∴AC=BF.
∵AC=BF,CE=CF,AE=BC,
∴△AEC≌△BCF(SSS);
(2)∵△AEC≌△BCF,
∴S△AEC=S△BCF,
∴S四边形ACFE — S△AEC =S四边形ACFE —S△BCF,
突破 4 找全等(二) SAS
1. B 解:∵AD+BC=AB,AD+BD=AB,
∴BD=BC.
∵BE=CA,∠DBE=∠C,
∴△BDE≌△CBA(SAS),
∴∠BDE=∠CBA=75°.
∵∠C=62°,
∴∠AFD=∠BDE--∠A=75°- 故选 B.
2.证明:∵∠ACD+∠DCB=∠ACB,∠ABC+∠DCB=∠ADC,∠ADC=∠ACB,
∴∠ACD=∠ABC.
∵AF平分∠EAC,
∴∠EAF=∠CAF.
∵AB=AE+BE,AB=BE+AC,
∴AE=AC.
在△AEF 和△ACF 中,
∴△AEF≌△ACF(SAS),
∴∠AEF=∠ACF.
∵∠ACD=∠ABC,
∴∠ABC=∠AEF,
∴EF∥BC.
3. C 解:∵∠AOB=∠COD=α,∴∠AOB + ∠BOC = ∠COD +∠BOC,
∴∠AOC=∠BOD,
∴△AOC≌△BOD(SAS),
∴∠A=∠B,
∴∠AOB=∠AMB=α.
α.故选 C.
4.132° 解:∵∠ACB=∠ECD=90°,∴∠BCD=∠ACE.
在△BDC 和△AEC 中,
∴△BDC≌△AEC(SAS),
∴∠DBC=∠EAC.
∵∠EBD=∠DBC+∠EBC=42°,
∴∠EAC+∠EBC=42°,
48°,
∴∠AEB = 180° (∠ABE + .故答案为 132°.
5.证明:∵∠BAC=∠DAE,
∴ ∠BAC - ∠BAE = ∠DAE -∠BAE,
∴∠BAD=∠EAC.
又∵AD=AE,AB=AC,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠DBA=∠C.
∵AB=AC,
∴∠C=∠ABC.
∵DF∥BC,
∴∠DFB=∠ABC=∠C=∠DBA.即∠DFB=∠DBF,
∴DF=DB,
∴DF=CE.
突破 5 找全等(三) ASA、AAS
1. C 解:∵CE⊥BD,
∴∠BEF=90°.
∵∠BAC=90°,
∴∠CAF=90°,
∴∠FAC=∠BAD=90°.
∵∠ABD+∠F=90°,∠ACF+∠F=90°,
∴∠ABD=∠ACF.
在△ABD 和△ACF 中,
∴△ABD≌△ACF(ASA),
∴AD=AF.
∵AB=AC,D 为AC中点,
∴AB=AC=2AD=2AF.
∵BF=AB+AF=12,
∴3AF=12,
∴AF=4,
∴AB=AC=2AF=8,
∴△FBC 的面积是 故选 C.
2.证明:∵∠EDA=∠ABC=∠EAC=90°,
∴∠EAD + ∠CAB = ∠ACB +∠CAB=90°,
∴∠EAD=∠ACB.
∵EA=AC,
∴△ABC≌△EDA(AAS),
∴AF=AB=ED,AD=BC.
∵AF⊥AB,
∴∠EDA=∠FAD=90°.
∵∠EOD=∠FOA,
∴△AOF≌△DOE(AAS),
∴OA=OD,
∴AD=2OA,
∴BC=2OA.
3. 解:∵∠ACB=90°,
∴∠BCE+∠ECA=90°,
∵AD⊥CE,
∴∠CAD+∠ECA=90°,
∴∠CAD=∠BCE.
在△ACD 与△CBE 中,
∴△ACD≌△CBE(AAS),
∴BE=CD,CE=AD=8,
∴BE=CD=CE--DE=8-5=3,
故答案为
4.解:(1)∵∠ACB=90°,BE⊥CE,∴∠ECB+∠ACD=90°,∠ECB+∠CBE=90°,
∴∠ACD=∠CBE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
∵AC=BC,
∴△ACD≌△CBE(AAS),
∴CD=BE;
(2)∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∵FD=CD,
∴FD=BE,
∵AD⊥CE,BE⊥CE,
∴∠BEG=∠FDG=90°,
∵∠FGD=∠BGE,
∴△FDG≌△BEG(AAS),
∴EG=DG,
∵AD=5,BE=2,
突破 6 找全等(四) HL
1.证明:过点 D 作 DG⊥AC 于点 G.
∵AD 是角平分线,DE⊥AB 于点E,DG⊥AC,
∴DG=DE,
∴Rt△FGD≌Rt△BED(HL),Rt△AGD≌Rt△AED(HL),
∴FG=BE,AG=AE,
∴AB-AF=AB-(AG--FG)=AB--(AE--BE)=AB-AE+BE=2BE.
2.证明:(1)∵AD是△ABC的中线,
∴BD=CD.
∵BE⊥AD,CF⊥AD,
∴∠BED=∠F,
∴△BED≌△CFD(AAS),
∴BE=CF;
(2)在 Rt△BGE 和 Rt△CAF 中,
∴Rt△BGE≌Rt△CAF(HL),
∴GE=AF,
∴AG=EF.
∵△BED≌△CFD,
∴DE=DF,
∴GA=2DE.
3. 解:∵EP⊥AB,AH是高,
∴∠P=∠AHB=90°.
∵AE∥BC,
∴∠EAP=∠CBA.
在△AEP 和△BAH 中,
∴△AEP≌△BAH(AAS),
∴PE=AH,AP=BH=1.
在 Rt△DEP 和 Rt△CAH 中,
∴Rt△DEP≌Rt△CAH(HL),
∴CH=DP.设 AD=x,则 CH=DP=x+1.
4.解:如图1所示,
∵AM,DN 分别为 BC,EF 边上的高,
∴△ACM 和△DFN 均为直角三角形.
∵在 Rt△ACM 和 Rt△DFN 中,
∴Rt△ACM≌Rt△DFN(HL),
∴∠DFE=∠ACB=50°;如图 2 所示,
∵AM,DN分别为 BC,EF 边上的高,
∴△ACM 和△DFN 均为直角三角形,
∴Rt△ACM≌Rt△DFN(HL),
∴∠DFN=∠ACB=50°,
∴∠DFE=130°.
综上所述,∠DFE 的度数为 50°或130°.
突破 7 找全等(五)
等线段代换证和差
1.证明:由条件可得△ACE≌△ABD(SAS),
∴BD=CE,
∴BC=CD+BD=CD+CE.
2.证明:(1)易得 △ABD ≌△CAE(AAS),
∴AD=CE,AE=BD,
∴DE=AD+AE=CE+BD;
(2)同(1)AD=CE,AE=BD,
∴DE=AD-AE=CE--BD.
3.15 解:设AB 分别交CE,CD 于点G,H,则∠AGE=∠CGH.
∵AB⊥CD,CE⊥AD,BF⊥AD,
∴∠AHC = ∠AEC = ∠CED =
∴∠A = 90°— ∠AGE = 90°—∠CGH=∠C.
∵AB=CD,
∴△ABF≌△CDE(AAS),
∴AF=CE=12,BF=DE=9,EF=6,
∴DF=DE--EF=9-6=3,
∴AD=AF+DF=12+3=15.
4.解:延长 DO 交 AB 于点 M,延长EO 交AB 于点 N.
∵BO 是∠ABC 的平分线,
∴∠OBE=∠OBN.
∵OE⊥OB,
∴∠BOE=∠BON=90°.
∴△BOE≌△BON(ASA).
同理可得,△AOD≌△AOM,
∴OE=ON,OD=OM,BE=BN,AD=AM.
∴△EOD≌△NOM(SAS),
∴DE=MN.
∴CE+CD+DE=BC-BE+AC-AD+MN=BC-(BM+MN)+AC--(AN+MN)+MN = BC-BM--MN+AC-AN=BC+AC-AB=4+3-5=2.
突破8 找全等(六) 全等计数
1. C 解:△ACE≌△DBF,△ACO≌△DBO,△ACB≌△DBC,△AEO≌ △DFO, △AEB ≌ △DFC,△ABO ≌ △DCO, △ABD ≌△DCA,共7 对.故选 C.
2. C 解:图1 中有 1 对三角形全等;图2 中有 3 对三角形全等;图3 中有6对三角形全等;由此发现,第n 个图 形 中 全 等 三 角 形 的 对 数 是 故选 C.
3. B 解:如图,共4个.故选 B.
4. D 解:以 AB 为公共边的有1个,以 AC 为公共边的有 3 个,以 BC 为公共边的有3个,共计7个.故选 D.
5. D 解:以AB 为公共边的三角形有3个,以BC 为公共边的三角形有0个,以AC 为公共边的三角形有 1个,共3+0+1=4个.故选 D.
6. B 解:共有 9 种情况.故选 B.
7. C 解:共2×4-1=7个.故选 C.
8. B 解:在每个 3×3 的网格中,与△ABC全等的格点三角形一共有 8个,
而网格中共有3×3的网格4个,∴共还有8×4-1=31(个).故选 B.
9.31 解:在 3 × 3 的 网 格中,与△ABC 全等的格点三角形(不含△ABC)一共有7个,
而网格中共有3×3的网格 4个,∴共有7×4+3=31个.
故答案为31.
突破9 找全等(七) 动点问题1. 或 解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=∠A+∠ACD=90°,
∴∠A=∠BCD.
∵∠ECF=∠BCD,
∴∠ECF=∠A.当 F 在C 上方时,
∵AB=CF,∠A=∠ECF,
∴当CE=AC=24 cm时,△ABC≌△CFE.
∵BE=BC+CE=7+24=31( cm),
当 F 在C下方时,
∵CF'=AB,∠BCD=∠A,
∴当 时,△ABC≌△CFE.
∴当 或 时,能使△ABC≌△CFE.故答案为 或
2.1 或 7 解:∵AB=CD,若∠ABP
=∠DCE=90°,BP=CE=2,
∴△ABP≌△DCE.
∵BP=2t=2,
∴t=1;
∵AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,
∴△BAP≌△DCE.
∵AP=16-2t=2,解得t=7.
综上,当t 的值为 1 或 7 秒时,△ABP 和△DCE 全等.故答案为1或 7.
3. C 解:当点 P 在AC 上时,
∵以 P,C,M 为顶点的三角形与△QCN 全等,
∴PC=CQ,
∴5-2t=6-3t,
∴t=1;
当点 P 在 AC 上,点Q 第一次从点C 返回时,
∵以P,C,M为
顶点的三角形与△QCN 全等,
∴PC=CQ,
∴5-2t=3t-6,
当点 P 在 CE 上,点 Q 第一次从 E点返回时,
∵以 P,C,M 为顶点的三角形与△QCN 全等,
∴PC=CQ,
∴2t-5=18-3t,
综上所述,t的值为 1 或 或 .故选 C.
4.解:①若△ACP≌△BPQ,则 AC=BP,AP=BQ,可得 解得
②若△ACP≌△BQP,则AC=BQ,AP=BP,可得 解得 综上所述,当△ACP 与△BPQ全等时,x的值为2 或
5.1或1.2 解:设点 F 的运动速度为x cm/s,则AE=t cm,
BE=(5-t) cm,BF= xt cm,
∵∠DAB=∠ABC,
∴当AD=BE,AE=BF时,
根据“SAS”判断△ADE≌△BEF,
即5-t=3,t= xt,解得t=2,x=1;
当 AD = BF,AE = BE 时, 根 据
“SAS”判断△ADE≌△BFE,
即 xt=3,t=5-t,
解得t=2.5,x=1.2.
综上所述,点 F 的运动速度为 1 cm/s或1.2cm/s.
6.18或70 解:由题意知,BE : BF=3:7,设BE=3t,则 BF=7t,AE=60-3t;
①当△AEG≌△BFE时,AE=BF,∴60-3t=7t,t=6,
∴AG=BE=3t=18;
②当△AEG≌△BEF时,AE=BE,60-3t=3t,t=10,AG=BF=7t=70.
故 AG=18或 70.
