五年级上册数学6 梯形的面积 课件(共21张PPT)人教版
文档属性
| 名称 | 五年级上册数学6 梯形的面积 课件(共21张PPT)人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
人教版五年级上册
梯形的面积
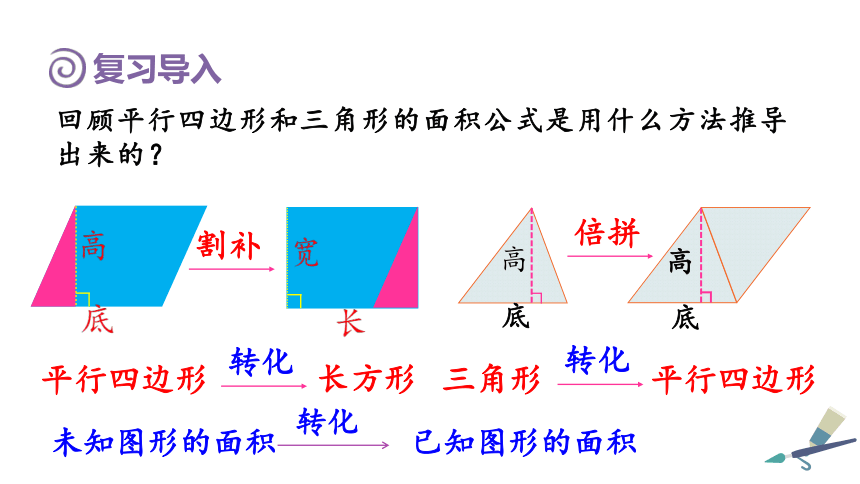
回顾平行四边形和三角形的面积公式是用什么方法推导出来的?
复习导入
割补
平行四边形
转化
长方形
高
底
倍拼
高
底
三角形
转化
平行四边形
未知图形的面积
转化
已知图形的面积
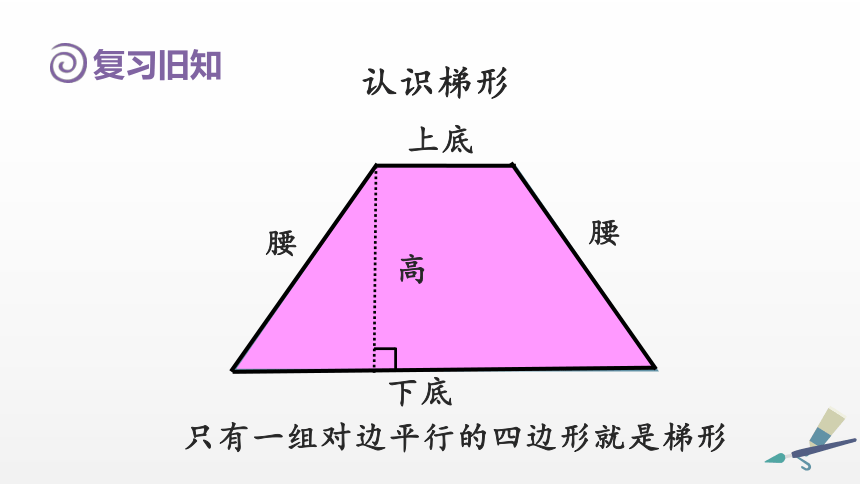
上底
下底
腰
腰
高
只有一组对边平行的四边形就是梯形
复习旧知
认识梯形
想一想:梯形能和我们学过的哪些图形建立联系?
梯形的面积
转化?
已知图形的面积
建立联系
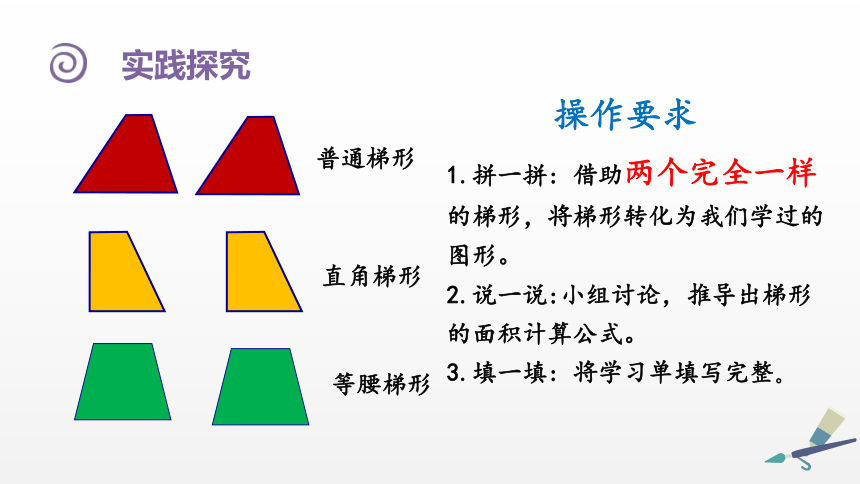
普通梯形
直角梯形
等腰梯形
普通梯形
直角梯形
等腰梯形
操作要求
1.拼一拼: 借助两个完全一样的梯形,将梯形转化为我们学过的图形。
2.说一说:小组讨论,推导出梯形的面积计算公式。
3.填一填: 将学习单填写完整。
实践探究
普通梯形
直角梯形
等腰梯形
推导过程
倍拼
倍拼
倍拼
梯形的面积=(上底+下底)×高÷2
推导过程
一个梯形能不能推导出梯形面积公式?
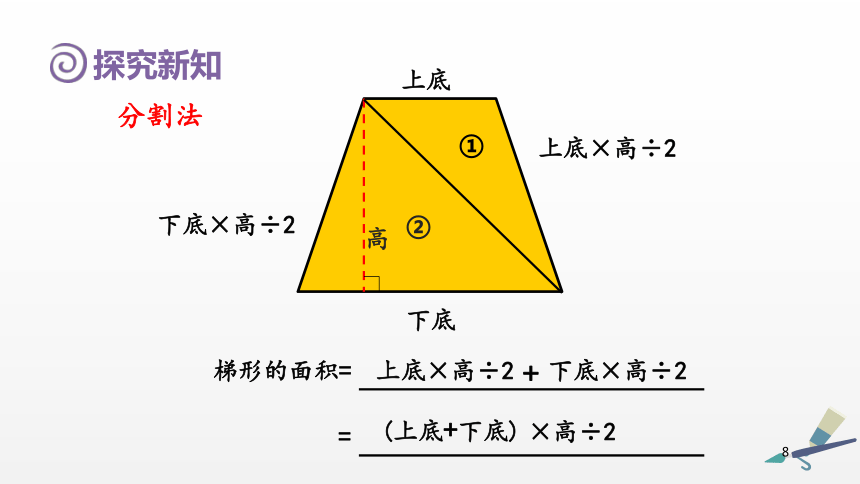
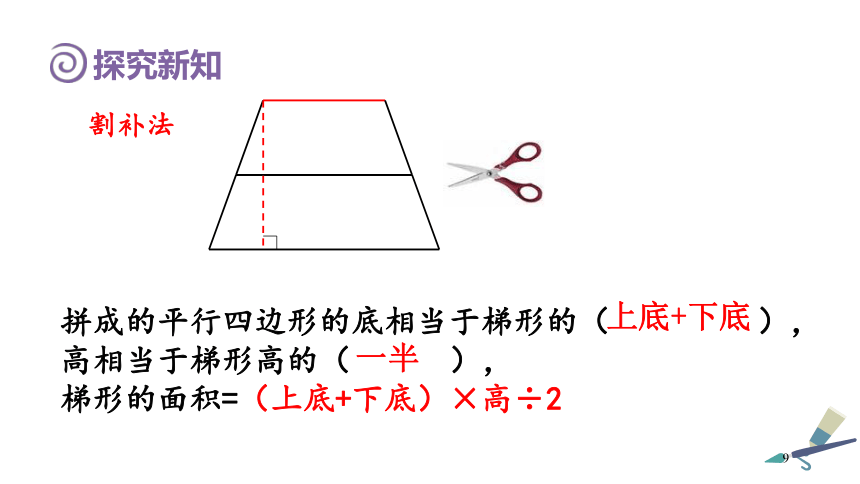
上底下底高①②上底×高÷2下底×高÷2梯形的面积=上底×高÷2下底×高÷2+=×高÷2(上底+下底)分割法探究新知拼成的平行四边形的底相当于梯形的( ),高相当于梯形高的( ),梯形的面积=(上底+下底)×高÷2上底+下底一半割补法探究新知
倍拼法
分割法
割补法
推导方法回顾
梯形面积 =(上底+下底)×高÷2
如果用S表示梯形的面积,用a表示梯形的上底,用b表示梯形的下底,用h表示梯形的高,梯形的面积计算公式可以写成:
a
h
b
探究新知
想一想:要求梯形的面积必须知道哪些条件 在计算的过程中要注意什么?
S=(a+b)h÷2
3
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
135 m
120 m
36 m
小提示:1. 先写字母公式
2.再代入数求值
3.最后加单位名称
3
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
135 m
120 m
36 m
s=(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 平方米。
计算下面每个梯形的面积。
30m
9m
18m
10m
26m
34m
1.
巩固练习
S =(a+b)h÷2
=(9+18)×10÷2
=27×10÷2
=135(m )
S =(a+b)h÷2
=(26+34)×30÷2
=60×30÷2
=900(m )
2.生活中圆木、钢管等经常像下图这样堆放,你能计算图中圆木的总根数吗?
小
提
示
将长度转化为根数,将高转化为层数。
提升练习
2.生活中圆木、钢管等经常像下图这样堆放,你能计算图中圆木的总根数吗?
S =(a+b)h÷2
=(2+6)×5÷2
= 8×5÷2
= 20(根)
答:这堆圆木共20根。
提升练习
梳理公式联系
你们能利用梯形的面积公式解决其它平面图形的面积吗?
3cm
6cm
4cm
3cm
梳理图形联系
这些图形的面积计算公式推导过程之间有什么联系?你能把这五种图形之间的联系用图表示出来吗?
h
a
a
b
s=ab
s=a2
a
a
h
s=ah
s=ah÷2
h
a
b
s=(a+b)h÷2
这节课你们都学会了哪些知识?
梯形的面积
b
a
h
梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
课堂小结
课后作业
1.思考还有其他方法可以推导梯形面积公式吗?
2.用自己的语言整理梯形面积的推导公式。
再 见
人教版五年级上册
梯形的面积
回顾平行四边形和三角形的面积公式是用什么方法推导出来的?
复习导入
割补
平行四边形
转化
长方形
高
底
倍拼
高
底
三角形
转化
平行四边形
未知图形的面积
转化
已知图形的面积
上底
下底
腰
腰
高
只有一组对边平行的四边形就是梯形
复习旧知
认识梯形
想一想:梯形能和我们学过的哪些图形建立联系?
梯形的面积
转化?
已知图形的面积
建立联系
普通梯形
直角梯形
等腰梯形
普通梯形
直角梯形
等腰梯形
操作要求
1.拼一拼: 借助两个完全一样的梯形,将梯形转化为我们学过的图形。
2.说一说:小组讨论,推导出梯形的面积计算公式。
3.填一填: 将学习单填写完整。
实践探究
普通梯形
直角梯形
等腰梯形
推导过程
倍拼
倍拼
倍拼
梯形的面积=(上底+下底)×高÷2
推导过程
一个梯形能不能推导出梯形面积公式?
上底下底高①②上底×高÷2下底×高÷2梯形的面积=上底×高÷2下底×高÷2+=×高÷2(上底+下底)分割法探究新知拼成的平行四边形的底相当于梯形的( ),高相当于梯形高的( ),梯形的面积=(上底+下底)×高÷2上底+下底一半割补法探究新知
倍拼法
分割法
割补法
推导方法回顾
梯形面积 =(上底+下底)×高÷2
如果用S表示梯形的面积,用a表示梯形的上底,用b表示梯形的下底,用h表示梯形的高,梯形的面积计算公式可以写成:
a
h
b
探究新知
想一想:要求梯形的面积必须知道哪些条件 在计算的过程中要注意什么?
S=(a+b)h÷2
3
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
135 m
120 m
36 m
小提示:1. 先写字母公式
2.再代入数求值
3.最后加单位名称
3
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
135 m
120 m
36 m
s=(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 平方米。
计算下面每个梯形的面积。
30m
9m
18m
10m
26m
34m
1.
巩固练习
S =(a+b)h÷2
=(9+18)×10÷2
=27×10÷2
=135(m )
S =(a+b)h÷2
=(26+34)×30÷2
=60×30÷2
=900(m )
2.生活中圆木、钢管等经常像下图这样堆放,你能计算图中圆木的总根数吗?
小
提
示
将长度转化为根数,将高转化为层数。
提升练习
2.生活中圆木、钢管等经常像下图这样堆放,你能计算图中圆木的总根数吗?
S =(a+b)h÷2
=(2+6)×5÷2
= 8×5÷2
= 20(根)
答:这堆圆木共20根。
提升练习
梳理公式联系
你们能利用梯形的面积公式解决其它平面图形的面积吗?
3cm
6cm
4cm
3cm
梳理图形联系
这些图形的面积计算公式推导过程之间有什么联系?你能把这五种图形之间的联系用图表示出来吗?
h
a
a
b
s=ab
s=a2
a
a
h
s=ah
s=ah÷2
h
a
b
s=(a+b)h÷2
这节课你们都学会了哪些知识?
梯形的面积
b
a
h
梯形的面积=(上底+下底)×高÷2
S=(a+b)h÷2
课堂小结
课后作业
1.思考还有其他方法可以推导梯形面积公式吗?
2.用自己的语言整理梯形面积的推导公式。
再 见
