12.2 三角形全等的判定 同步练习(4课时,无答案)2024--2025学年人教版八年级数学上册
文档属性
| 名称 | 12.2 三角形全等的判定 同步练习(4课时,无答案)2024--2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 611.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 19:20:21 | ||
图片预览

文档简介
12.2 三角形全等的判定
第1课时 用“SSS”判定三角形全等
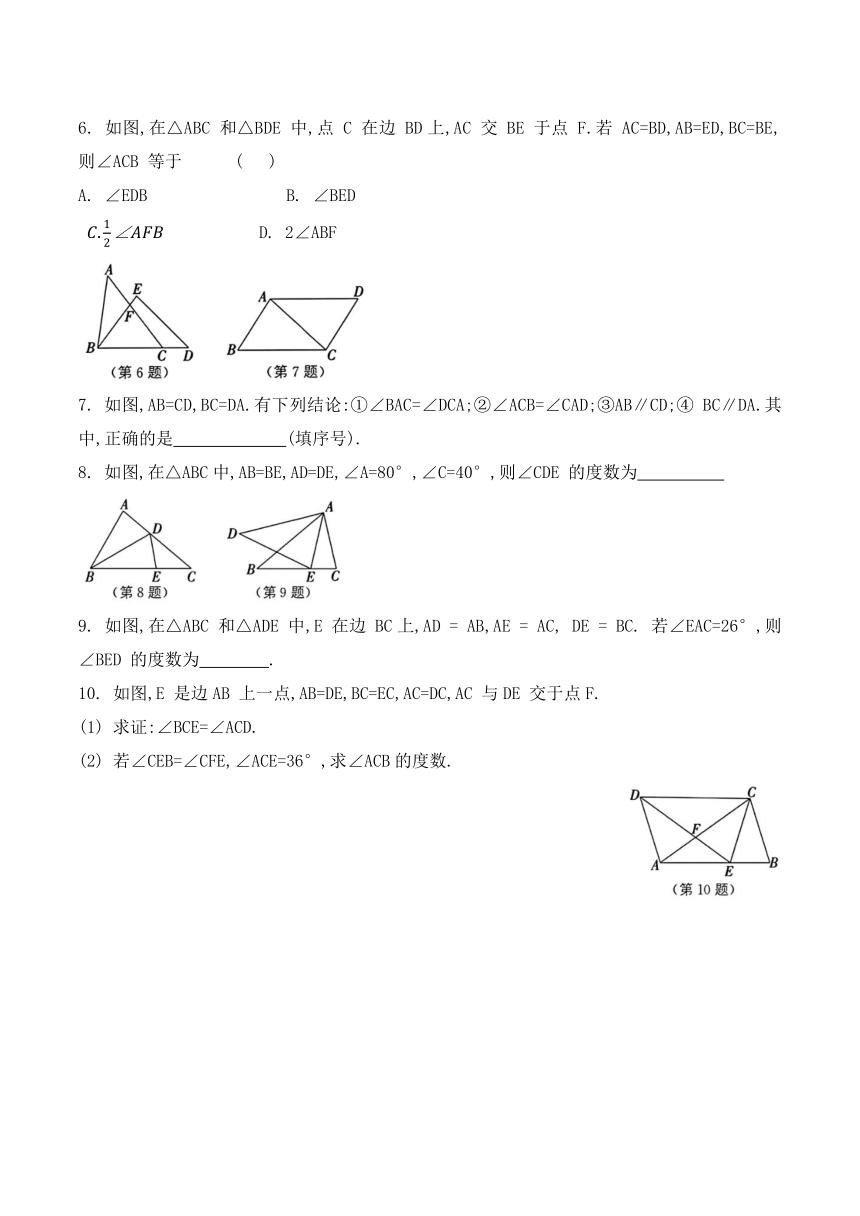
1. 如图,在△ABC 中,AB=AC,D 为BC的中点,则下列结论中,不一定正确的是 ( )
A. △ABD≌△ACD B. ∠B=∠C
C. AD 平分∠BAC D. AD=BD
2.如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论中,错误的是 ( )
A. △ABE≌△ACD B. △ABD≌△ACE
C. ∠ACE=30° D. ∠1=70°
3. 如图所示为小明制作的风筝,DE=DF,EH=FH.若∠EDH=43°,则∠EDF 的度数为 .
4. 如图,CA=CD,AB=DE,BC=EC,AC 与DE 相交于点F.若∠EFC=76°,∠D=42°,则∠BCE 的度数为 .
5. 如图,点A,C,D,B在同一条直线上,点 E,F 分别在直线AB 的两侧,AE=BF,CE=DF,AD=BC.
(1) 求证:△ACE≌△BDF.
(2) 若∠CDF=55°,求∠ACE 的度数.
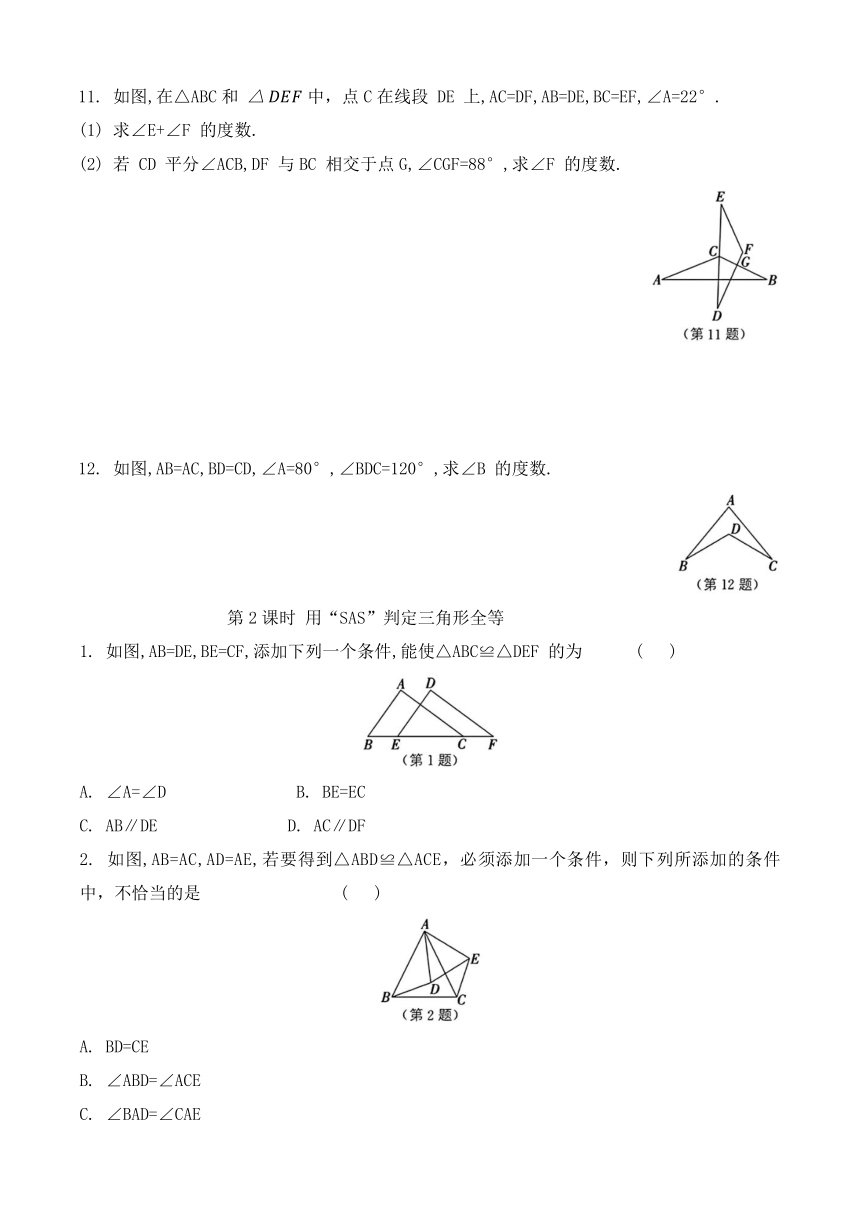
6. 如图,在△ABC 和△BDE 中,点 C 在边 BD上,AC 交 BE 于点 F.若 AC=BD,AB=ED,BC=BE,则∠ACB 等于 ( )
A. ∠EDB B. ∠BED
D. 2∠ABF
如图,AB=CD,BC=DA.有下列结论:①∠BAC=∠DCA;②∠ACB=∠CAD;③AB∥CD;④ BC∥DA.其中,正确的是 (填序号).
8. 如图,在△ABC中,AB=BE,AD=DE,∠A=80°,∠C=40°,则∠CDE 的度数为
9. 如图,在△ABC 和△ADE 中,E 在边 BC上,AD = AB,AE = AC, DE = BC. 若∠EAC=26°,则∠BED 的度数为 .
10. 如图,E 是边AB 上一点,AB=DE,BC=EC,AC=DC,AC 与DE 交于点F.
(1) 求证:∠BCE=∠ACD.
(2) 若∠CEB=∠CFE,∠ACE=36°,求∠ACB的度数.
如图,在△ABC和 中,点C在线段 DE 上,AC=DF,AB=DE,BC=EF,∠A=22°.
(1) 求∠E+∠F 的度数.
(2) 若 CD 平分∠ACB,DF 与BC 相交于点G,∠CGF=88°,求∠F 的度数.
12. 如图,AB=AC,BD=CD,∠A=80°,∠BDC=120°,求∠B 的度数.
第2课时 用“SAS”判定三角形全等
1. 如图,AB=DE,BE=CF,添加下列一个条件,能使△ABC≌△DEF 的为 ( )
A. ∠A=∠D B. BE=EC
C. AB∥DE D. AC∥DF
2. 如图,AB=AC,AD=AE,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添加的条件中,不恰当的是 ( )
A. BD=CE
B. ∠ABD=∠ACE
C. ∠BAD=∠CAE
D. ∠BAC=∠DAE
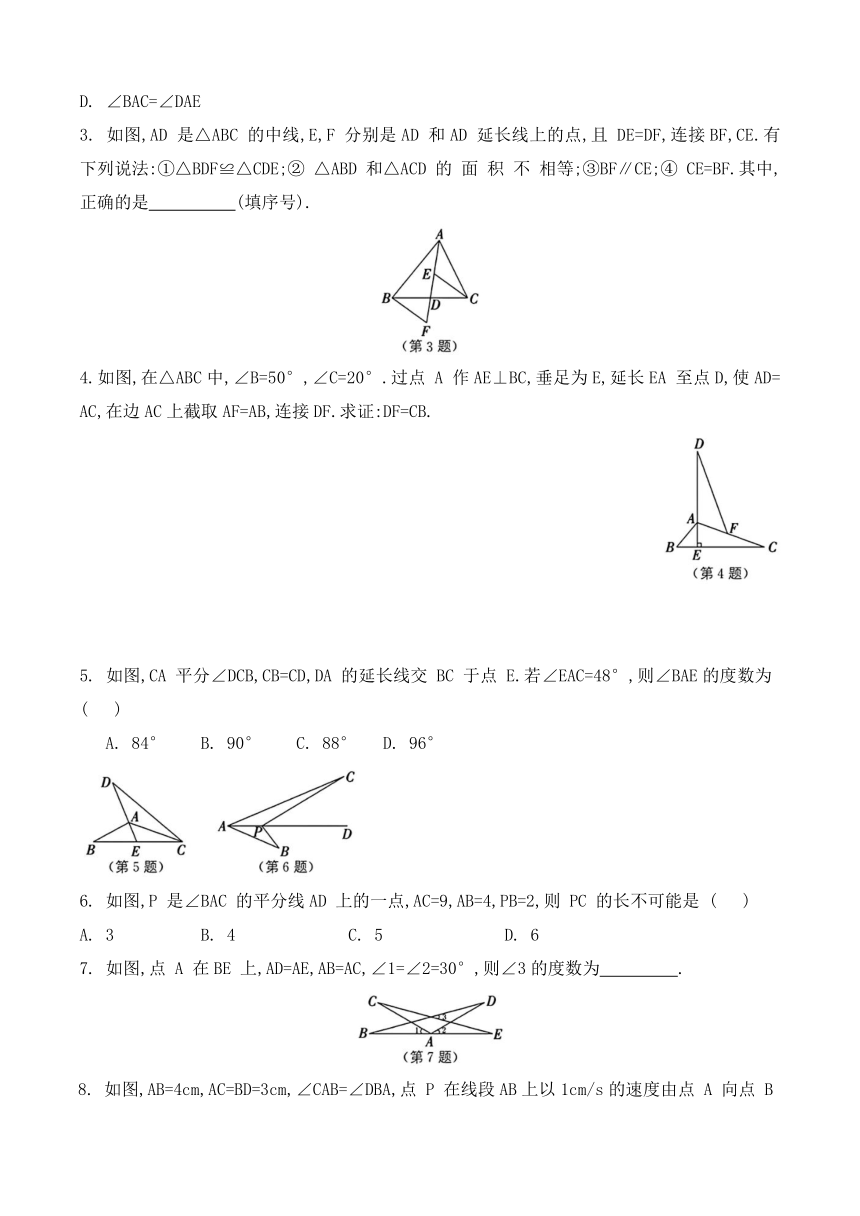
3. 如图,AD 是△ABC 的中线,E,F 分别是AD 和AD 延长线上的点,且 DE=DF,连接BF,CE.有下列说法:①△BDF≌△CDE;② △ABD 和△ACD 的 面 积 不 相等;③BF∥CE;④ CE=BF.其中,正确的是 (填序号).
4.如图,在△ABC中,∠B=50°,∠C=20°.过点 A 作AE⊥BC,垂足为E,延长EA 至点D,使AD=AC,在边AC上截取AF=AB,连接DF.求证:DF=CB.
5. 如图,CA 平分∠DCB,CB=CD,DA 的延长线交 BC 于点 E.若∠EAC=48°,则∠BAE的度数为 ( )
A. 84° B. 90° C. 88° D. 96°
6. 如图,P 是∠BAC 的平分线AD 上的一点,AC=9,AB=4,PB=2,则 PC 的长不可能是 ( )
A. 3 B. 4 C. 5 D. 6
7. 如图,点 A 在BE 上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为 .
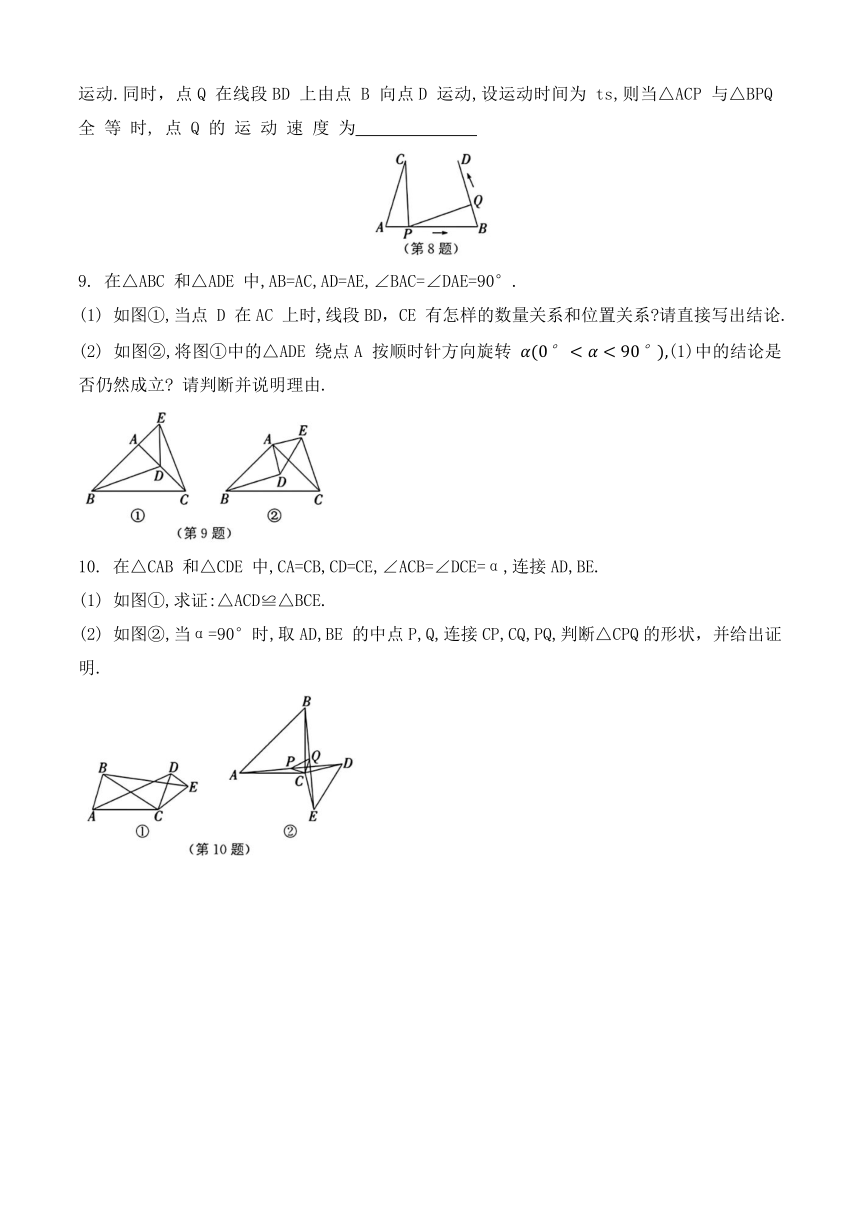
8. 如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点 P 在线段AB上以1cm/s的速度由点 A 向点 B 运动.同时,点Q 在线段BD 上由点 B 向点D 运动,设运动时间为 ts,则当△ACP 与△BPQ 全 等 时, 点 Q 的 运 动 速 度 为
9. 在△ABC 和△ADE 中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1) 如图①,当点 D 在AC 上时,线段BD,CE 有怎样的数量关系和位置关系 请直接写出结论.
(2) 如图②,将图①中的△ADE 绕点A 按顺时针方向旋转 (1)中的结论是否仍然成立 请判断并说明理由.
10. 在△CAB 和△CDE 中,CA=CB,CD=CE,∠ACB=∠DCE=α,连接AD,BE.
(1) 如图①,求证:△ACD≌△BCE.
(2) 如图②,当α=90°时,取AD,BE 的中点P,Q,连接CP,CQ,PQ,判断△CPQ的形状,并给出证明.
用“ASA”或“AAS”判定三角形全等
1. 如图,甲、乙、丙三个三角形中,和△ABC 全等的图形是 ( )
A. 只有乙 B. 只有丙
C. 甲和乙 D. 乙和丙
2. 如图,在△ABC 中,F 是高AD 和高BE 的交点,BD=12,DC=9,AD=BD,则线段AF的长为( )
A. 1 B. 2
C. 4 D. 3
3. 如图,AB∥CF,E 是DF 的中点.若AB=9,CF=6,则BD= .
4.如图,在△ABC 和△AEF中,点E 在边BC上,∠C=∠F,AC=AF,∠CAF=∠BAE,EF与AC交于点G.
(1) 求证:△ABC≌△AEF.
(2) 若∠B=55°,∠C=20°,求∠EAC 的度数.
5. 如图,AD 平分∠BAC,AB=AC,连接BD,CD,延长BD 交AC 于点F,延长CD 交AB于点E,则图中的全等三角形有 ( )
A. 2 对 B. 3对 C. 4 对 D. 1对
6. 如图,在四边形ABCD 中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 ( )
A. 15 B. 12.5 C. 14.5 D. 17
7. 如图,AB=10,∠A=∠B=45°,AC=BD= 点E,F 在线段AB 上,连接CE,DF.有下列条件:①CE=DF=4;②AF=BE;③∠CEB=∠DFA. 请在所给的条件中选择一个条件,使得△ACE 一定和△BDF 全等,则这个条件可以为 (填序号,写出所有正确的答案).
8. 如 图, 在 △ABC 中, BD 平 分∠ABC,AD⊥BD.若△BCD 的面积为 45,△ADC 的面积为 20,则 △ABD 的面积为 .
9.如图,在四边形ABCD 中,AD∥BC,E 为CD 的中点,连接AE,BE,延长 AE 交 BC的延长线于点 F.
(1) 判断AD 与FC 之间的数量关系,并说明理由.
(2) 若AB=BC+AD,判断BE与AF 之间的位置关系,并说明理由.
如图,在平面直角坐标系中,直线AB,ON 交于点Q,且 过A,B两点分别作 于点M,. 于点 N.若 4,则 MN 的长为 .
11. 如图,在△ABC中,AC=BC,延长AC到点E,过点 E 作EF⊥AB,交 AB 的延长线于点F,延长CB 到点G,过点G 作GH⊥AB,交AB 的延长线于点H,且EF=GH.
(1) 求证:△AEF≌△BGH.
(2) 连接EG,交FH 于点 D.若AB=4,求DH 的长.
用“HL”判定三角形全等
1. 如图,AB⊥AC于点A,BD⊥CD 于点 D.若AC=DB,则下列结论中,不正确的是( )
A. ∠A=∠D
B. ∠ABC=∠DCB
C. OB=CD
D. OA=OD
2. 根据下列已知条件,不能画出唯一的△ABC的是 ( )
A. ∠A=60°,∠B=45°,AB=4
B. ∠A=30°,AB=5,BC=3
C. ∠B=60°,AB=6,BC=10
D. ∠C=90°,AB=5,BC=3
3. 如图,在△ABC 中,∠C=90°,AD=AC,DE⊥AB 交 BC 于点 E.若∠B =28°,则∠AEC 的度数为 .
4. 如图,MN∥PQ,AB⊥PQ,点 A,D 在直线MN上,点 B,C 在直线 PQ 上,点 E 在AB上,AD+BC=7,AD=EB,DE=EC,则AB 的长为 .
5. 如图,在四边形 ABCD 中,∠ABC =∠ADC=90°,BE⊥AC 于点E,DF⊥AC 于点F,AE=CF,BC=DA.求证:Rt△ABE≌Rt△CDF.
6. 如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB 于点E,BD 和CE 交于点O,连接AO 并延长,交BC 于点F,则图中全等的直角三角形有 ( )
A. 4 对 B. 5对
C. 6 对 D. 7 对
7. 如图,BD=CF,FD⊥BC于点D,DE⊥AB于点 E,BE = CD. 若∠AFD = 145°, 则∠EDF 的度数为 .
8. 如图,在 Rt△ABC 中,∠C=90°,AC=8,BC=4,PQ=AB,P,Q两点分别在线段 AC 和过点 A 且垂直 于AC 的射线 AO 上运动. 当△ABC 和△PQA 全等时,AP 的长为 .
9. 八年级数学社团活动课上,同学们讨论了这样一道题:如图,在△ABE 和△ACD 中,∠BAC 是钝角,AB=AC,点 D,E 分别在边AB,AC 上,且 CD=BE.求证:∠AEB=∠ADC.
其中一名同学的解法如下:
在△ABE 和△ACD 中,
∴△ABE≌△ACD.
∴∠AEB=∠ADC.
这种解法遭到了其他同学的质疑,理由是不能用“SSA”证明三角形全等.请你给出这道题的正确解法.
10. 如图, 在△ABC 和△ADE 中,AB=AC,AD = AE,∠BAC =∠DAE,CE 的延长线交 BD 于点F.
(1) 求证:△ACE≌△ABD.
(2) 若∠BAC = ∠DAE = 50°, 请 求 出∠BFC的度数.
(3) 过点 A 作 AH⊥BD 于点 H,求证:EF+DH=HF.
第1课时 用“SSS”判定三角形全等
1. 如图,在△ABC 中,AB=AC,D 为BC的中点,则下列结论中,不一定正确的是 ( )
A. △ABD≌△ACD B. ∠B=∠C
C. AD 平分∠BAC D. AD=BD
2.如图,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论中,错误的是 ( )
A. △ABE≌△ACD B. △ABD≌△ACE
C. ∠ACE=30° D. ∠1=70°
3. 如图所示为小明制作的风筝,DE=DF,EH=FH.若∠EDH=43°,则∠EDF 的度数为 .
4. 如图,CA=CD,AB=DE,BC=EC,AC 与DE 相交于点F.若∠EFC=76°,∠D=42°,则∠BCE 的度数为 .
5. 如图,点A,C,D,B在同一条直线上,点 E,F 分别在直线AB 的两侧,AE=BF,CE=DF,AD=BC.
(1) 求证:△ACE≌△BDF.
(2) 若∠CDF=55°,求∠ACE 的度数.
6. 如图,在△ABC 和△BDE 中,点 C 在边 BD上,AC 交 BE 于点 F.若 AC=BD,AB=ED,BC=BE,则∠ACB 等于 ( )
A. ∠EDB B. ∠BED
D. 2∠ABF
如图,AB=CD,BC=DA.有下列结论:①∠BAC=∠DCA;②∠ACB=∠CAD;③AB∥CD;④ BC∥DA.其中,正确的是 (填序号).
8. 如图,在△ABC中,AB=BE,AD=DE,∠A=80°,∠C=40°,则∠CDE 的度数为
9. 如图,在△ABC 和△ADE 中,E 在边 BC上,AD = AB,AE = AC, DE = BC. 若∠EAC=26°,则∠BED 的度数为 .
10. 如图,E 是边AB 上一点,AB=DE,BC=EC,AC=DC,AC 与DE 交于点F.
(1) 求证:∠BCE=∠ACD.
(2) 若∠CEB=∠CFE,∠ACE=36°,求∠ACB的度数.
如图,在△ABC和 中,点C在线段 DE 上,AC=DF,AB=DE,BC=EF,∠A=22°.
(1) 求∠E+∠F 的度数.
(2) 若 CD 平分∠ACB,DF 与BC 相交于点G,∠CGF=88°,求∠F 的度数.
12. 如图,AB=AC,BD=CD,∠A=80°,∠BDC=120°,求∠B 的度数.
第2课时 用“SAS”判定三角形全等
1. 如图,AB=DE,BE=CF,添加下列一个条件,能使△ABC≌△DEF 的为 ( )
A. ∠A=∠D B. BE=EC
C. AB∥DE D. AC∥DF
2. 如图,AB=AC,AD=AE,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添加的条件中,不恰当的是 ( )
A. BD=CE
B. ∠ABD=∠ACE
C. ∠BAD=∠CAE
D. ∠BAC=∠DAE
3. 如图,AD 是△ABC 的中线,E,F 分别是AD 和AD 延长线上的点,且 DE=DF,连接BF,CE.有下列说法:①△BDF≌△CDE;② △ABD 和△ACD 的 面 积 不 相等;③BF∥CE;④ CE=BF.其中,正确的是 (填序号).
4.如图,在△ABC中,∠B=50°,∠C=20°.过点 A 作AE⊥BC,垂足为E,延长EA 至点D,使AD=AC,在边AC上截取AF=AB,连接DF.求证:DF=CB.
5. 如图,CA 平分∠DCB,CB=CD,DA 的延长线交 BC 于点 E.若∠EAC=48°,则∠BAE的度数为 ( )
A. 84° B. 90° C. 88° D. 96°
6. 如图,P 是∠BAC 的平分线AD 上的一点,AC=9,AB=4,PB=2,则 PC 的长不可能是 ( )
A. 3 B. 4 C. 5 D. 6
7. 如图,点 A 在BE 上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为 .
8. 如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点 P 在线段AB上以1cm/s的速度由点 A 向点 B 运动.同时,点Q 在线段BD 上由点 B 向点D 运动,设运动时间为 ts,则当△ACP 与△BPQ 全 等 时, 点 Q 的 运 动 速 度 为
9. 在△ABC 和△ADE 中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1) 如图①,当点 D 在AC 上时,线段BD,CE 有怎样的数量关系和位置关系 请直接写出结论.
(2) 如图②,将图①中的△ADE 绕点A 按顺时针方向旋转 (1)中的结论是否仍然成立 请判断并说明理由.
10. 在△CAB 和△CDE 中,CA=CB,CD=CE,∠ACB=∠DCE=α,连接AD,BE.
(1) 如图①,求证:△ACD≌△BCE.
(2) 如图②,当α=90°时,取AD,BE 的中点P,Q,连接CP,CQ,PQ,判断△CPQ的形状,并给出证明.
用“ASA”或“AAS”判定三角形全等
1. 如图,甲、乙、丙三个三角形中,和△ABC 全等的图形是 ( )
A. 只有乙 B. 只有丙
C. 甲和乙 D. 乙和丙
2. 如图,在△ABC 中,F 是高AD 和高BE 的交点,BD=12,DC=9,AD=BD,则线段AF的长为( )
A. 1 B. 2
C. 4 D. 3
3. 如图,AB∥CF,E 是DF 的中点.若AB=9,CF=6,则BD= .
4.如图,在△ABC 和△AEF中,点E 在边BC上,∠C=∠F,AC=AF,∠CAF=∠BAE,EF与AC交于点G.
(1) 求证:△ABC≌△AEF.
(2) 若∠B=55°,∠C=20°,求∠EAC 的度数.
5. 如图,AD 平分∠BAC,AB=AC,连接BD,CD,延长BD 交AC 于点F,延长CD 交AB于点E,则图中的全等三角形有 ( )
A. 2 对 B. 3对 C. 4 对 D. 1对
6. 如图,在四边形ABCD 中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为 ( )
A. 15 B. 12.5 C. 14.5 D. 17
7. 如图,AB=10,∠A=∠B=45°,AC=BD= 点E,F 在线段AB 上,连接CE,DF.有下列条件:①CE=DF=4;②AF=BE;③∠CEB=∠DFA. 请在所给的条件中选择一个条件,使得△ACE 一定和△BDF 全等,则这个条件可以为 (填序号,写出所有正确的答案).
8. 如 图, 在 △ABC 中, BD 平 分∠ABC,AD⊥BD.若△BCD 的面积为 45,△ADC 的面积为 20,则 △ABD 的面积为 .
9.如图,在四边形ABCD 中,AD∥BC,E 为CD 的中点,连接AE,BE,延长 AE 交 BC的延长线于点 F.
(1) 判断AD 与FC 之间的数量关系,并说明理由.
(2) 若AB=BC+AD,判断BE与AF 之间的位置关系,并说明理由.
如图,在平面直角坐标系中,直线AB,ON 交于点Q,且 过A,B两点分别作 于点M,. 于点 N.若 4,则 MN 的长为 .
11. 如图,在△ABC中,AC=BC,延长AC到点E,过点 E 作EF⊥AB,交 AB 的延长线于点F,延长CB 到点G,过点G 作GH⊥AB,交AB 的延长线于点H,且EF=GH.
(1) 求证:△AEF≌△BGH.
(2) 连接EG,交FH 于点 D.若AB=4,求DH 的长.
用“HL”判定三角形全等
1. 如图,AB⊥AC于点A,BD⊥CD 于点 D.若AC=DB,则下列结论中,不正确的是( )
A. ∠A=∠D
B. ∠ABC=∠DCB
C. OB=CD
D. OA=OD
2. 根据下列已知条件,不能画出唯一的△ABC的是 ( )
A. ∠A=60°,∠B=45°,AB=4
B. ∠A=30°,AB=5,BC=3
C. ∠B=60°,AB=6,BC=10
D. ∠C=90°,AB=5,BC=3
3. 如图,在△ABC 中,∠C=90°,AD=AC,DE⊥AB 交 BC 于点 E.若∠B =28°,则∠AEC 的度数为 .
4. 如图,MN∥PQ,AB⊥PQ,点 A,D 在直线MN上,点 B,C 在直线 PQ 上,点 E 在AB上,AD+BC=7,AD=EB,DE=EC,则AB 的长为 .
5. 如图,在四边形 ABCD 中,∠ABC =∠ADC=90°,BE⊥AC 于点E,DF⊥AC 于点F,AE=CF,BC=DA.求证:Rt△ABE≌Rt△CDF.
6. 如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB 于点E,BD 和CE 交于点O,连接AO 并延长,交BC 于点F,则图中全等的直角三角形有 ( )
A. 4 对 B. 5对
C. 6 对 D. 7 对
7. 如图,BD=CF,FD⊥BC于点D,DE⊥AB于点 E,BE = CD. 若∠AFD = 145°, 则∠EDF 的度数为 .
8. 如图,在 Rt△ABC 中,∠C=90°,AC=8,BC=4,PQ=AB,P,Q两点分别在线段 AC 和过点 A 且垂直 于AC 的射线 AO 上运动. 当△ABC 和△PQA 全等时,AP 的长为 .
9. 八年级数学社团活动课上,同学们讨论了这样一道题:如图,在△ABE 和△ACD 中,∠BAC 是钝角,AB=AC,点 D,E 分别在边AB,AC 上,且 CD=BE.求证:∠AEB=∠ADC.
其中一名同学的解法如下:
在△ABE 和△ACD 中,
∴△ABE≌△ACD.
∴∠AEB=∠ADC.
这种解法遭到了其他同学的质疑,理由是不能用“SSA”证明三角形全等.请你给出这道题的正确解法.
10. 如图, 在△ABC 和△ADE 中,AB=AC,AD = AE,∠BAC =∠DAE,CE 的延长线交 BD 于点F.
(1) 求证:△ACE≌△ABD.
(2) 若∠BAC = ∠DAE = 50°, 请 求 出∠BFC的度数.
(3) 过点 A 作 AH⊥BD 于点 H,求证:EF+DH=HF.
