考点六:锐角三角函数—三年(2022-2024)中考数学真题分类汇编(含解析)
文档属性
| 名称 | 考点六:锐角三角函数—三年(2022-2024)中考数学真题分类汇编(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 18:59:54 | ||
图片预览



文档简介
考点六:锐角三角函数—三年(2022-2024)中考数学真题分类汇编
一、解答题
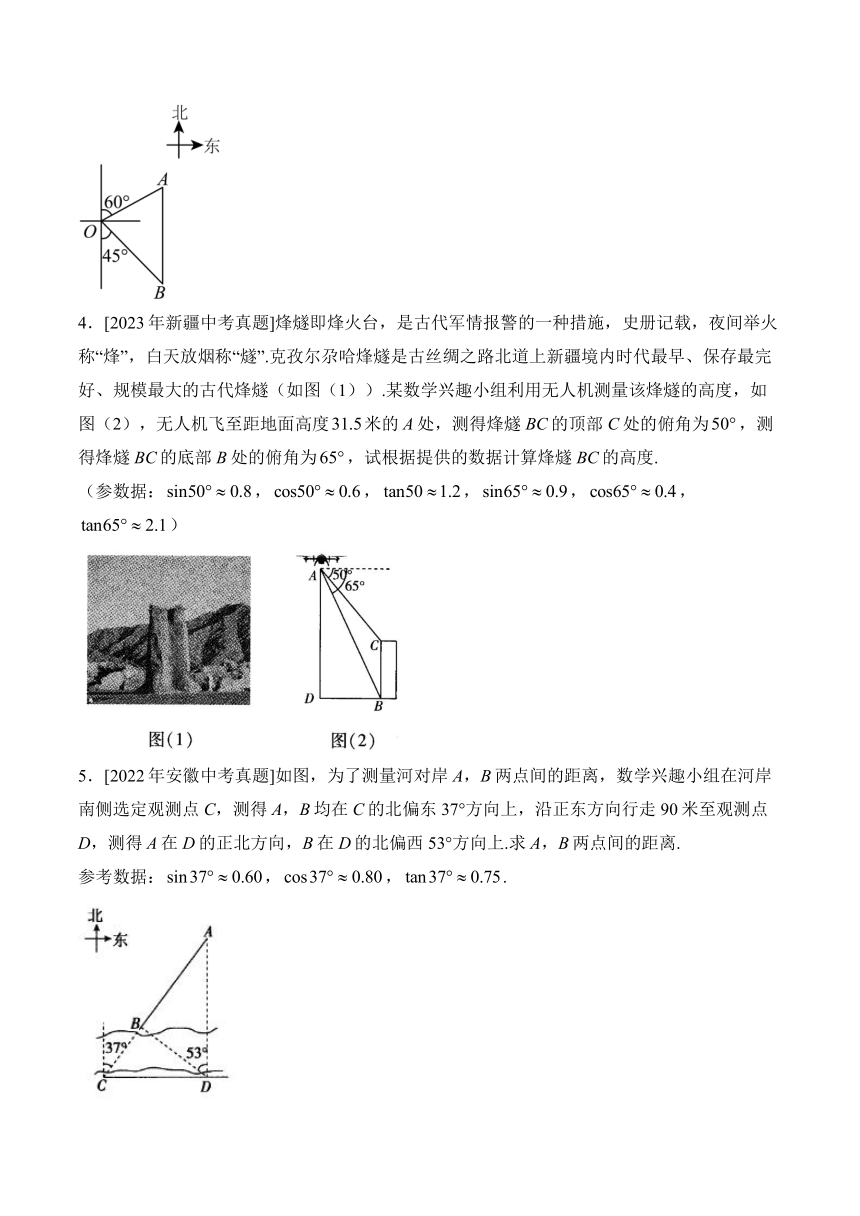
1.[2022年吉林中考真题]动感单车是一种新型的运动器械.图①是一辆动感单车的实物图,图②是其侧面示意图.为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm,的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度(结果精确到1cm).(参考数据:,,)
2.[2024年陕西中考真题]如图所示,一座小山顶的水平观景台的海拔高度为,小明想利用这个观景台测量对面山顶C点处的海拔高度,他在该观景台上选定了一点A,在点A处测得C点的仰角,再在上选一点B,在点B处测得C点的仰角,.求山顶C点处的海拔高度.(小明身高忽略不计,参考数据:,,)
3.[2023年西藏中考真题]如图,轮船甲和轮船乙同时离开海港O,轮船甲沿北偏东的方向航行,轮船乙沿东南方向航行,2小时后,轮船甲到达A处,轮船乙到达B处,此时轮船甲正好在轮船乙的正北方向.已知轮船甲的速度为每小时25海里,求轮船乙的速度.(结果保留根号)
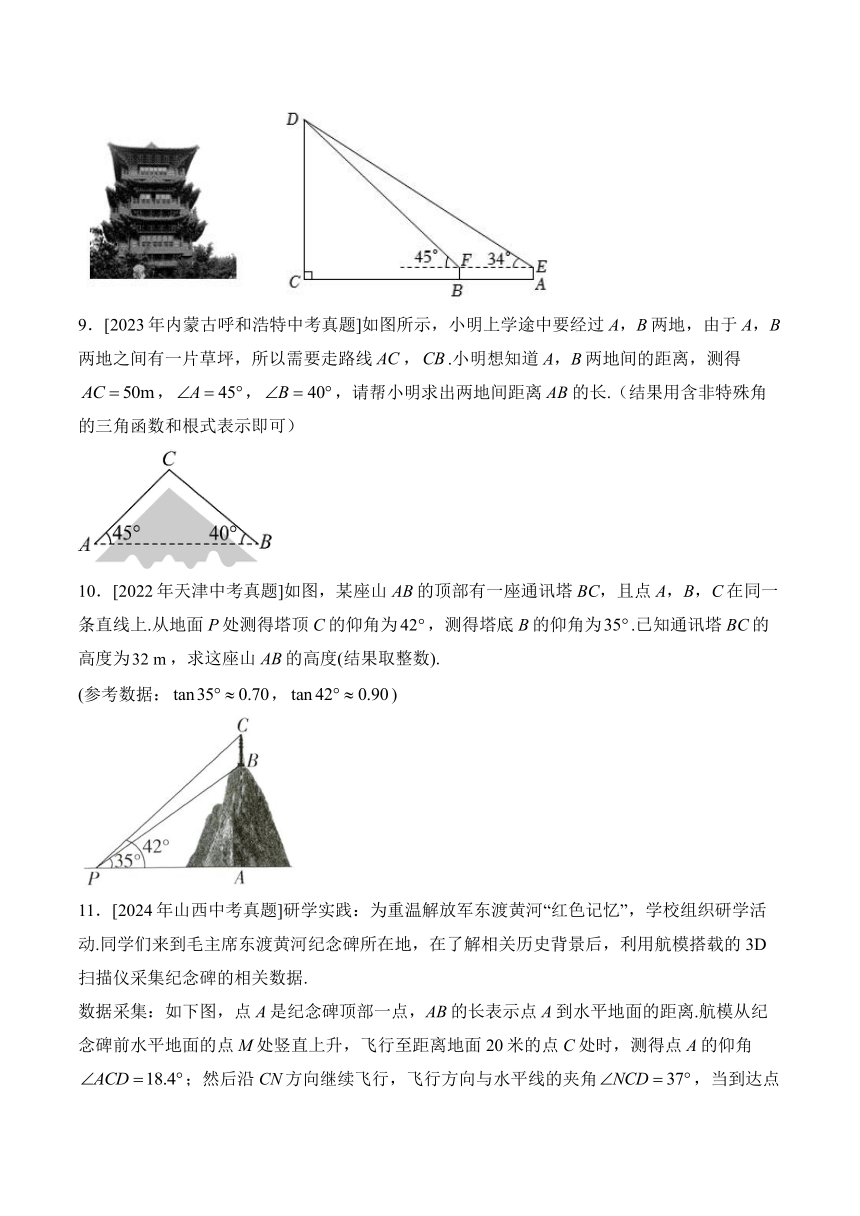
4.[2023年新疆中考真题]烽燧即烽火台,是古代军情报警的一种措施,史册记载,夜间举火称“烽”,白天放烟称“燧”.克孜尔尕哈烽燧是古丝绸之路北道上新疆境内时代最早、保存最完好、规模最大的古代烽燧(如图(1)).某数学兴趣小组利用无人机测量该烽燧的高度,如图(2),无人机飞至距地面高度米的A处,测得烽燧BC的顶部C处的俯角为,测得烽燧BC的底部B处的俯角为,试根据提供的数据计算烽燧BC的高度.
(参数据:,,,,,)
5.[2022年安徽中考真题]如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向,B在D的北偏西53°方向上.求A,B两点间的距离.
参考数据:,,.
6.[2023年安徽中考真题]如图,O,R是同一水平线上的两点,无人机从O点竖直上升到A点时,测得A到R点的距离为40 m,R点的俯角为,无人机继续竖直上升到点,测得R点的俯角为.求无人机从A点到点的上升高度AB(精确到0.1 m).
参考数据:,,,,,.
7.[2022年新疆中考真题]周末,王老师布置了一项综合实践作业,要求利用所学知识测量一栋楼的高度.小希站在自家阳台上,看对面一栋楼顶部的仰角为,看这栋楼底部的俯角为,已知两楼之间的水平距离为,求这栋楼的高度.(参考数据:,,)
8.[2022年河南中考真题]开封清明上河图是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15 m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5 m,测量点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度(结果精确到1 m.参考数据:,,).
9.[2023年内蒙古呼和浩特中考真题]如图所示,小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线,.小明想知道A,B两地间的距离,测得,,,请帮小明求出两地间距离的长.(结果用含非特殊角的三角函数和根式表示即可)
10.[2022年天津中考真题]如图,某座山AB的顶部有一座通讯塔BC,且点A,B,C在同一条直线上.从地面P处测得塔顶C的仰角为,测得塔底B的仰角为.已知通讯塔BC的高度为,求这座山AB的高度(结果取整数).
(参考数据:,)
11.[2024年山西中考真题]研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.
数据采集:如下图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角;然后沿CN方向继续飞行,飞行方向与水平线的夹角,当到达点A正上方的点E处时,测得米;…
数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计 纪念碑顶部点A到地面的距离AB的长(结果精确到1米.参考数据:,,,,,).
12.[2024年西藏中考真题]在数学综合实践活动中,次仁和格桑自主设计了“测量家附近的一座小山高度”的探究作业.如图,次仁在A处测得山顶C的仰角为;格桑在B处测得山顶C的仰角为.已知两人所处位置的水平距离米,A处距地面的垂直高度米,B处距地面的垂直高度米,点M,F,N在同一条直线上,求小山的高度.(结果保留根号)
13.[2024年天津中考真题]综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点C,D,E依次在同一条水平直线上,,,垂足为C.在D处测得桥塔顶部B的仰角()为,测得桥塔底部A的俯角()为,又在E处测得桥塔顶部B的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).
参考数据:,.
14.[2024年海南中考真题]木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,如图所示.
航行记录一:上午8时,渔船到达木兰灯塔P北偏西方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5海里内,会出现异常海况,点C位于木兰灯塔P北偏东方向.
请你根据以上信息解决下列问题:
(1)填空:________°,________°,________海里;
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:,,)
参考答案
1.答案:88cm
解析:在中,,,,
.
答:点A到CD的距离AE的长度约为88 cm.
2.答案:山顶C点处的海拔高度为.
解析:过点C作交的延长线于点D,设,
在中,,
,
在中,,
,
,
,
解得,
山顶C点处的海拔高度为.
3.答案:海里/小时.
解析:过O作于D,
在中,,(海里),
(海里),
在中,,
(海里),
轮船乙的速度为海里小时.
4.答案:烽燧BC的高度为
解析:如图,过点A作BC的垂线,交BC的延长线于点E.
由题意易知,四边形ADBE是矩形,.
在中,,,
.
在中,,,
,
.
答:烽燧BC的高度为.
5.答案:A,B两点间的距离为96 m.
解析:如图,由题意知,,,,,,
,,,
,
,即.
在中,.
在中,.
答:A,B两点间的距离为96 m.
6.答案:10.9米
解析:由题意,得,.
在中,,,
.
在中,,
,
.
答:无人机从A点到B点的上升高度AB约为10.9 m.
7.答案:这栋楼的高度为:米
解析:过A作于E,
∴
由依题意得:,,,
和中,
∵,
∴,
∴
∴这栋楼的高度为:米.
8.答案:32 m
解析:如图,延长EF交DC于点H,由题意知,.
设.
在中,,
.
在中,,
.
,,即,
,
.
答:拂云阁DC的高度约为32 m.
9.答案:
解析:过C作于H,如图:
在中,,,
,,
在中,,,
,
;
两地间距离的长为.
10.答案:
解析:根据题意,,,.
在中,,
.
在中,,
.
,
,
.
答:这座山AB的高度约为.
11.答案:27米
解析:延长CD交AB于点H.
由题意得,四边形CMBH为矩形.
.
在中,,,
,,
在中,,,
,.
设.
,,.
解得.
(米)
答:点A到地面的距离AB的长约为27米.
12.答案:米
解析:根据题意可得:,,
∴四边形和四边形为矩形,
∴米,米,,,
∴(米),
设,则米,
∵,,
∴,
∵,,
∴,
∴,,
∵米,
∴,
解得:,
∴米.
13.答案:(1)
(2)
解析:(I)设,由,得.
,垂足为C,
.
在中,,,
.
在中,,,
.
.得.
答:线段的长约为.
(II)在中,,,
.
.
答:桥塔的高度约为.
14.答案:(1)30;75;5
(2)该渔船不改变航线与速度,会进入“海况异常”区
解析:(1)如图所示,过点P作于D,
由题意得,,,,
,;
一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,上午8时从A出发到上午8时30分到达B,
海里.
(2)设海里,
在中,海里,
在中,海里,海里,
,,
解得,
海里,
,,
海里;
上午9时,船距离A的距离为海里,
,
该渔船不改变航线与速度,会进入“海况异常”区.
一、解答题
1.[2022年吉林中考真题]动感单车是一种新型的运动器械.图①是一辆动感单车的实物图,图②是其侧面示意图.为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm,的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度(结果精确到1cm).(参考数据:,,)
2.[2024年陕西中考真题]如图所示,一座小山顶的水平观景台的海拔高度为,小明想利用这个观景台测量对面山顶C点处的海拔高度,他在该观景台上选定了一点A,在点A处测得C点的仰角,再在上选一点B,在点B处测得C点的仰角,.求山顶C点处的海拔高度.(小明身高忽略不计,参考数据:,,)
3.[2023年西藏中考真题]如图,轮船甲和轮船乙同时离开海港O,轮船甲沿北偏东的方向航行,轮船乙沿东南方向航行,2小时后,轮船甲到达A处,轮船乙到达B处,此时轮船甲正好在轮船乙的正北方向.已知轮船甲的速度为每小时25海里,求轮船乙的速度.(结果保留根号)
4.[2023年新疆中考真题]烽燧即烽火台,是古代军情报警的一种措施,史册记载,夜间举火称“烽”,白天放烟称“燧”.克孜尔尕哈烽燧是古丝绸之路北道上新疆境内时代最早、保存最完好、规模最大的古代烽燧(如图(1)).某数学兴趣小组利用无人机测量该烽燧的高度,如图(2),无人机飞至距地面高度米的A处,测得烽燧BC的顶部C处的俯角为,测得烽燧BC的底部B处的俯角为,试根据提供的数据计算烽燧BC的高度.
(参数据:,,,,,)
5.[2022年安徽中考真题]如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向,B在D的北偏西53°方向上.求A,B两点间的距离.
参考数据:,,.
6.[2023年安徽中考真题]如图,O,R是同一水平线上的两点,无人机从O点竖直上升到A点时,测得A到R点的距离为40 m,R点的俯角为,无人机继续竖直上升到点,测得R点的俯角为.求无人机从A点到点的上升高度AB(精确到0.1 m).
参考数据:,,,,,.
7.[2022年新疆中考真题]周末,王老师布置了一项综合实践作业,要求利用所学知识测量一栋楼的高度.小希站在自家阳台上,看对面一栋楼顶部的仰角为,看这栋楼底部的俯角为,已知两楼之间的水平距离为,求这栋楼的高度.(参考数据:,,)
8.[2022年河南中考真题]开封清明上河图是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15 m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5 m,测量点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度(结果精确到1 m.参考数据:,,).
9.[2023年内蒙古呼和浩特中考真题]如图所示,小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线,.小明想知道A,B两地间的距离,测得,,,请帮小明求出两地间距离的长.(结果用含非特殊角的三角函数和根式表示即可)
10.[2022年天津中考真题]如图,某座山AB的顶部有一座通讯塔BC,且点A,B,C在同一条直线上.从地面P处测得塔顶C的仰角为,测得塔底B的仰角为.已知通讯塔BC的高度为,求这座山AB的高度(结果取整数).
(参考数据:,)
11.[2024年山西中考真题]研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.
数据采集:如下图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角;然后沿CN方向继续飞行,飞行方向与水平线的夹角,当到达点A正上方的点E处时,测得米;…
数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计 纪念碑顶部点A到地面的距离AB的长(结果精确到1米.参考数据:,,,,,).
12.[2024年西藏中考真题]在数学综合实践活动中,次仁和格桑自主设计了“测量家附近的一座小山高度”的探究作业.如图,次仁在A处测得山顶C的仰角为;格桑在B处测得山顶C的仰角为.已知两人所处位置的水平距离米,A处距地面的垂直高度米,B处距地面的垂直高度米,点M,F,N在同一条直线上,求小山的高度.(结果保留根号)
13.[2024年天津中考真题]综合与实践活动中,要用测角仪测量天津海河上一座桥的桥塔的高度(如图①).某学习小组设计了一个方案:如图②,点C,D,E依次在同一条水平直线上,,,垂足为C.在D处测得桥塔顶部B的仰角()为,测得桥塔底部A的俯角()为,又在E处测得桥塔顶部B的仰角()为.
(1)求线段的长(结果取整数);
(2)求桥塔的高度(结果取整数).
参考数据:,.
14.[2024年海南中考真题]木兰灯塔是亚洲最高、世界第二高的航标灯塔,位于海南岛的最北端,是海南岛东北部最重要的航标.某天,一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,如图所示.
航行记录一:上午8时,渔船到达木兰灯塔P北偏西方向上的A处. 记录二:上午8时30分,渔船到达木兰灯塔P北偏西方向上的B处. 记录三:根据气象观测,当天凌晨4时到上午9时,受天文大潮和天气影响,琼州海峡C点周围5海里内,会出现异常海况,点C位于木兰灯塔P北偏东方向.
请你根据以上信息解决下列问题:
(1)填空:________°,________°,________海里;
(2)若该渔船不改变航线与速度,是否会进入“海况异常”区,请计算说明.
(参考数据:,,)
参考答案
1.答案:88cm
解析:在中,,,,
.
答:点A到CD的距离AE的长度约为88 cm.
2.答案:山顶C点处的海拔高度为.
解析:过点C作交的延长线于点D,设,
在中,,
,
在中,,
,
,
,
解得,
山顶C点处的海拔高度为.
3.答案:海里/小时.
解析:过O作于D,
在中,,(海里),
(海里),
在中,,
(海里),
轮船乙的速度为海里小时.
4.答案:烽燧BC的高度为
解析:如图,过点A作BC的垂线,交BC的延长线于点E.
由题意易知,四边形ADBE是矩形,.
在中,,,
.
在中,,,
,
.
答:烽燧BC的高度为.
5.答案:A,B两点间的距离为96 m.
解析:如图,由题意知,,,,,,
,,,
,
,即.
在中,.
在中,.
答:A,B两点间的距离为96 m.
6.答案:10.9米
解析:由题意,得,.
在中,,,
.
在中,,
,
.
答:无人机从A点到B点的上升高度AB约为10.9 m.
7.答案:这栋楼的高度为:米
解析:过A作于E,
∴
由依题意得:,,,
和中,
∵,
∴,
∴
∴这栋楼的高度为:米.
8.答案:32 m
解析:如图,延长EF交DC于点H,由题意知,.
设.
在中,,
.
在中,,
.
,,即,
,
.
答:拂云阁DC的高度约为32 m.
9.答案:
解析:过C作于H,如图:
在中,,,
,,
在中,,,
,
;
两地间距离的长为.
10.答案:
解析:根据题意,,,.
在中,,
.
在中,,
.
,
,
.
答:这座山AB的高度约为.
11.答案:27米
解析:延长CD交AB于点H.
由题意得,四边形CMBH为矩形.
.
在中,,,
,,
在中,,,
,.
设.
,,.
解得.
(米)
答:点A到地面的距离AB的长约为27米.
12.答案:米
解析:根据题意可得:,,
∴四边形和四边形为矩形,
∴米,米,,,
∴(米),
设,则米,
∵,,
∴,
∵,,
∴,
∴,,
∵米,
∴,
解得:,
∴米.
13.答案:(1)
(2)
解析:(I)设,由,得.
,垂足为C,
.
在中,,,
.
在中,,,
.
.得.
答:线段的长约为.
(II)在中,,,
.
.
答:桥塔的高度约为.
14.答案:(1)30;75;5
(2)该渔船不改变航线与速度,会进入“海况异常”区
解析:(1)如图所示,过点P作于D,
由题意得,,,,
,;
一艘渔船自西向东(沿方向)以每小时10海里的速度在琼州海峡航行,上午8时从A出发到上午8时30分到达B,
海里.
(2)设海里,
在中,海里,
在中,海里,海里,
,,
解得,
海里,
,,
海里;
上午9时,船距离A的距离为海里,
,
该渔船不改变航线与速度,会进入“海况异常”区.
同课章节目录
