考点三:函数—三年(2022-2024)中考数学真题分类汇编(含解析)
文档属性
| 名称 | 考点三:函数—三年(2022-2024)中考数学真题分类汇编(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 00:00:00 | ||
图片预览



文档简介
考点三:函数—三年(2022-2024)中考数学真题分类汇编
一、单选题
1.[2023年广西中考真题]将抛物线向右平移3个单位,再向上平移4个单位,得到的抛物线的解析式是( )
A. B.
C. D.
2.[2023年云南中考真题]若点是反比例函数图象上一点,则常数k的值为( )
A.3 B.-3 C. D.
3.[2024年广东中考真题]已知不等式的解集是,则一次函数的图象大致是( )
A. B.
C. D.
4.[2022年青海中考真题]2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )
A. B. C. D.
5.[2024年广东中考真题]若点,,都在二次函数的图象上,则( )
A. B. C. D.
6.[2023年河南中考真题]二次函数的图象如图所示,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.[2023年青海中考真题]生物兴趣小组探究酒精对某种鱼类的心率是否有影响,实验得出心率与酒精浓度的关系如图所示,下列说法正确的是( )
A.酒精浓度越大,心率越高
B.酒精对这种鱼类的心率没有影响
C.当酒精浓度是时,心率是168次/分
D.心率与酒精浓度是反比例函数关系
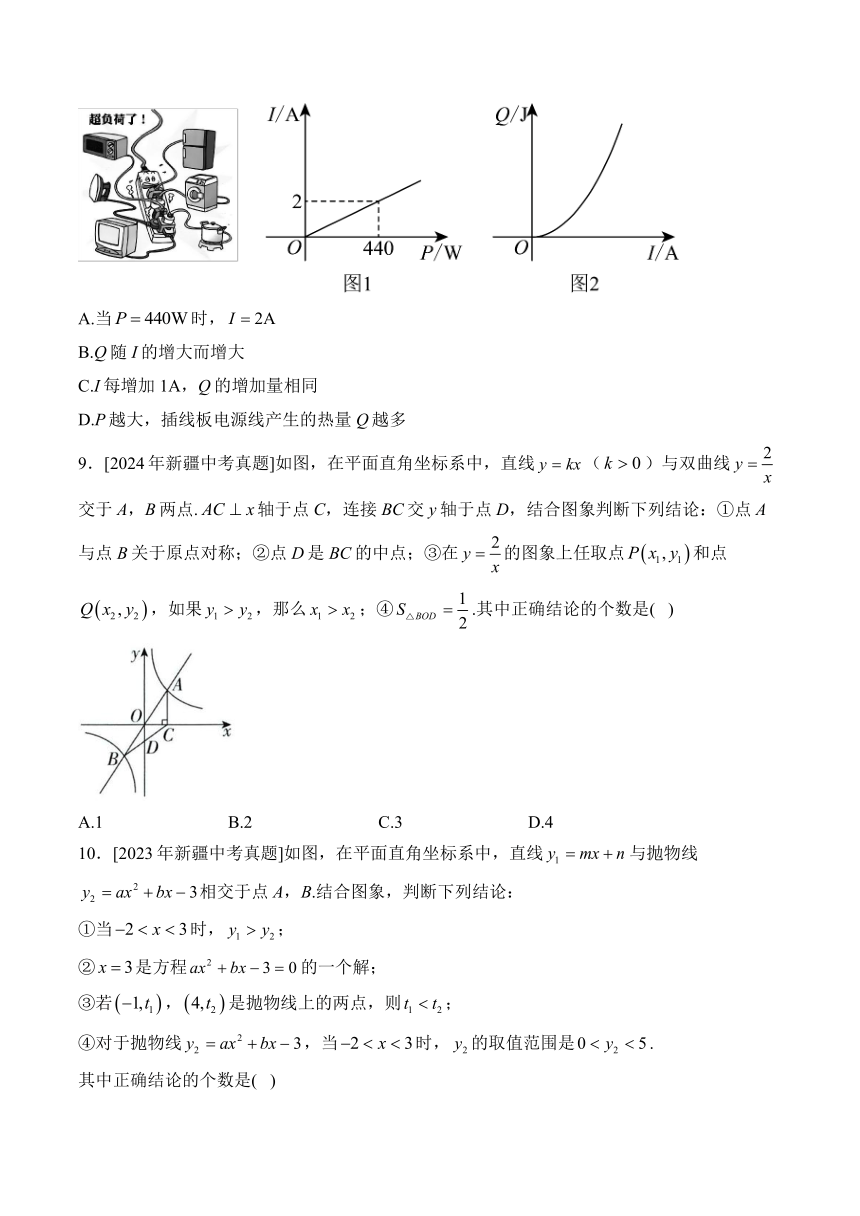
8.[2024年河南中考真题]把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( )
A.当时,
B.Q随I的增大而增大
C.I每增加1A,Q的增加量相同
D.P越大,插线板电源线产生的热量Q越多
9.[2024年新疆中考真题]如图,在平面直角坐标系中,直线()与双曲线交于A,B两点.轴于点C,连接BC交y轴于点D,结合图象判断下列结论:①点A与点B关于原点对称;②点D是BC的中点;③在的图象上任取点和点,如果,那么;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.[2023年新疆中考真题]如图,在平面直角坐标系中,直线与抛物线相交于点A,B.结合图象,判断下列结论:
①当时,;
②是方程的一个解;
③若,是抛物线上的两点,则;
④对于抛物线,当时,的取值范围是.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
二、填空题
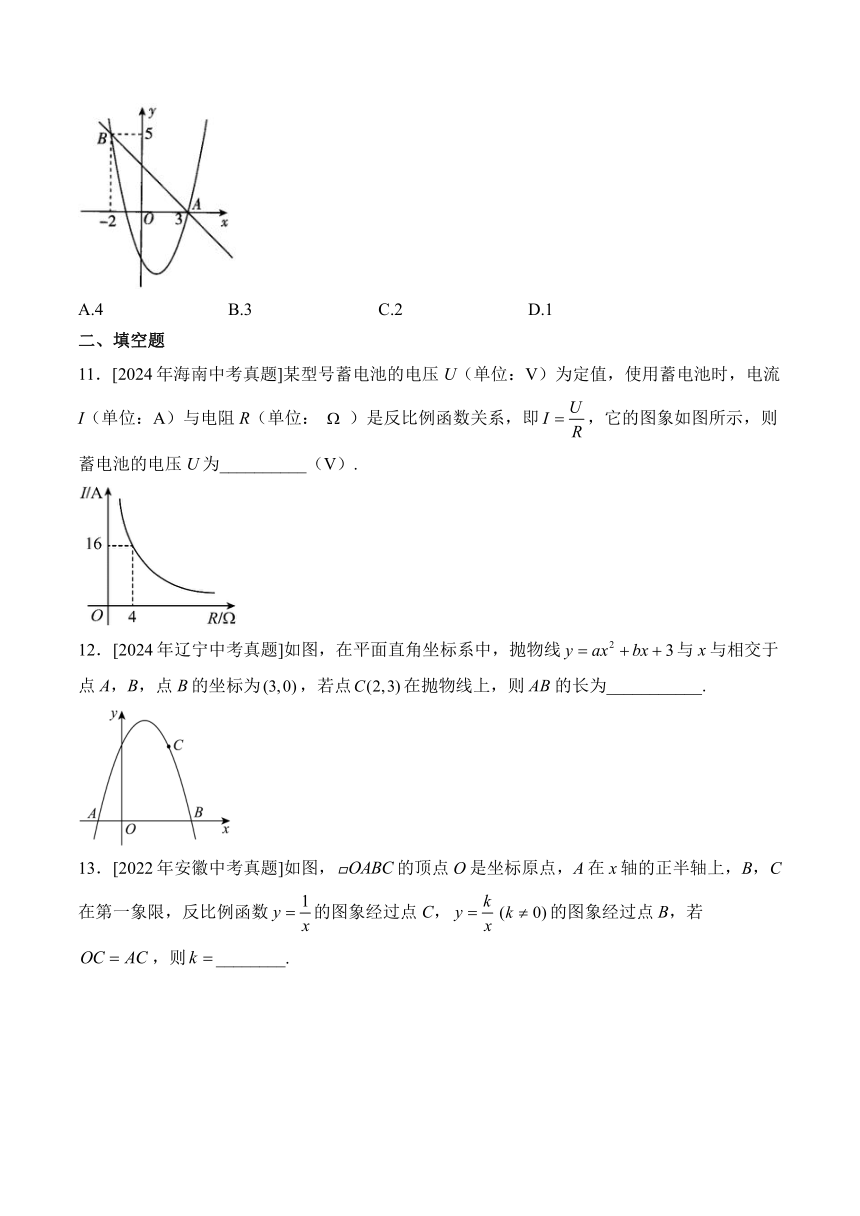
11.[2024年海南中考真题]某型号蓄电池的电压U(单位:V)为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,即,它的图象如图所示,则蓄电池的电压U为__________(V).
12.[2024年辽宁中考真题]如图,在平面直角坐标系中,抛物线与x与相交于点A,B,点B的坐标为,若点在抛物线上,则的长为___________.
13.[2022年安徽中考真题]如图,的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B,若,则________.
14.[2024年新疆中考真题]如图,抛物线与y轴交于点A,与x轴交于点B,线段CD在抛物线的对称轴上移动(点C在点D下方),且.当的值最小时,点C的坐标为__________.
三、解答题
15.[2022年北京中考真题]在平面直角坐标系xOy中,函数的图象经过点,,且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当时,对于x的每一个值,函数的值大于函数的值,直接写出n的取值范围.
16.[2023年河南中考真题]小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网AB与y轴的水平距离,,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
17.[2023年江西中考真题]如图,已知直线与反比例函数的图象交于点,与y轴交于点B,过点B作x轴的平行线交反比例函数的图象于点C.
(1)求直线AB和反比例函数图象的表达式;
(2)求的面积.
18.[2024年新疆中考真题]某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额(万元)与销售量x(吨)的函数解析式为:;成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
(1)求出成本关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?
(注:利润=销售额-成本)
19.[2023年云南中考真题]数和形是数学研究客观物体的两个方面.数(代数)侧重研究物体数量方面,具有精确性;形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的公共点中有整点?若存在,求所有整数a的值;若不存在,请说明理由.
20.[2023年重庆中考真题]如图,在平面直角坐标系中,抛物线与轴交于点A,,x与y轴交于点C,其中,.
(1)求该抛物线的表达式;
(2)点P是直线AC下方抛物线上一动点,过点P作于点D,求PD的最大值及此时点P的坐标;
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
参考答案
1.答案:A
解析:抛物线的顶点坐标是,将点向右平移93个单位,再向上平移4个单位,得到平移后抛物线的顶点坐标为,即.
抛物线开口方向与形状不变,故平移后抛物线的解析式为.
2.答案:A
3.答案:B
解析:A.不等式的解集是,故本选项不符合题意;
B.不等式的解集是,故本选项符合题意;
C.不等式的解集是,故本选项不符合题意;
D.不等式的解集是,故本选项不符合题意;
故选:B.
4.答案:B
解析:随着时间的增多,汽车离剧场的距离y(千米)减少,排除A、C、D;
由于途中停车加油耽误了几分钟,此时时间在增多,汽车离剧场的距离y没有变化;
后来加快了速度,仍保持匀速行进,所以后来的函数图象的走势应比前面匀速前进的走势要陡.故选:B.
5.答案:A
解析:二次函数,
该二次函数的抛物线开口向上,且对称轴为y轴.
当时,y随x的增大而增大,
,
,
故选:A.
6.答案:D
解析:由题图可得,,,的图象经过第一、二、三象限,不经过第四象限.
7.答案:C
解析:由图象可知,酒精浓度越大,心率越低,故A错误;
酒精浓度越大,心率越低,酒精对这种鱼类的心率有影响,故B错误;
由图象可知,当酒精浓度是时,心率是168次/分,故C正确;
任意取两个点坐标,,因为,所以心率与酒精浓度不是反比例函数关系,故D错误.
故选:C.
8.答案:C
解析:由图1可知,当时,,故选项A说法正确,不符合题意;
由图2可知,Q随I的增大而增大,故选项B说法正确,不符合题意;
由图2可知,I每增加1A,Q的增加量不相同故选项C说法错误,符合题意;
由图1可知I随P的增大而增大,由图2可知Q随T的增大而增大,所以P越大,插线板电源线产故选项D说法正确,不符合生的热量Q越多,不符合题意.
故选:C.
9.答案:C
解析:①反比例函数图象与正比例函数图象均关于原点成中心对称,
点A与点B关于原点对称,故①正确;
②点A与点B关于原点对称,.
轴,,是的中位线,
点D是BC的中点,故②正确;
③在每个象限内,y随x的增大而减小,
当P,Q不在同一象限,即点P在第一象限,点Q在第三象限时,;
当P,Q在同一象限时,,故③错误;
④,故④正确.其中正确的结论有①②④,共3个.故选C.
10.答案:B
解析:由图象,得当时,直线上的点位于抛物线上的点的上方,故,因此结论①正确;
由图象,得抛物线经过点,即当时,,故是方程的一个解,因此结论②正确;
将和分别代入,得解得
.
令,得,解得,.
当时,,当时,,则,因此结论③正确;
对于抛物线,若,则当时函数有最大值,最大值为5,
当时函数有最小值,最小值为-4,故的取值范围是,因此结论④错误.
11.答案:64
解析:设用电阻R表示电流I的函数解析式为,
过,
(V),
故答案为:64.
12.答案:4
解析:把点,点代入抛物线得,
,
解得,
抛物线,
令,得,
解得或,
,
;
故答案为:4.
13.答案:3
解析:由题知反比例函数的图象经过点C,设C点坐标为,
作于H,过A点作于G,
如图.四边形OABC是平行四边形,,
,,,
,,即.
的图象经过点B,.
14.答案:
解析:作A点关于对称轴的对称点,向下平移3个单位,得到,连接,交对称轴于点C,此时的值最小,
在中,
令,则,
,
令,则,
解得或,
点,
抛物线的对称轴为直线,
,
,
设直线的解析式为,
代入、B的坐标得,
解得,
直线的解析式为,
当时,,
.
故答案为.
15.答案:(1),
(2)
解析:(1)把,分别代入,
得解得
该函数的解析式为.
对于,当时,,
.
(2).
解法提示:函数的图象如图所示,易知当直线与y轴的交点与点A重合或在点A上方时符合题意,故.
16.答案:(1)-0.4
(2)选择吊球,使球的落地点到C点的距离更近
解析:(1)依题意知,点P为直线与y轴的交点.
当时,,点P的坐标为.
抛物线经过点P,,解得.
(2),,.
若选择扣球,当时,得,解得,
此时,球的落地点到C点的距离为.
若选择吊球,由(1)知,.
当时,得,解得,(舍),
此时球的落地点到C点的距离为.
,应选择吊球.
17.答案:(1)直线AB的表达式为,反比例函数图象的表达式为
(2)
解析:(1)直线与反比例函数的图象交于点,
,,
,,
直线AB的表达式为,反比例函数图象的表达式为.
(2)易得.
轴,
C点的纵坐标为1,BC与x轴的距离为1.
令,得,.
如图,过点A作于点D,
则,
.
18.答案:(1)
(2)
(3)见解析
解析:(1)为抛物线的顶点,
可设抛物线的函数解析式为.
将代入,
得,,
抛物线的函数解析式为.
(2)当时,最小,最小值为万元.
对于,当时,,
此时.
答:成本最低时,所获利润为万元.
(3)设当销售量为x时,利润为w万元.
则.
,
时,w取最大值,最大值是7.
答:当销售量为3吨时,可获得最大利润,最大利润是7万元
19.答案:(1)证明见解析
(2)存在,整数a的值为0,,1或-2
解析:(1),即时,函数的解析式可化为,为一次函数,
当时,图象T与x轴有公共点.
当,即时,函数为二次函数,
,
当时,图象T与x轴总有公共点.
综上可知,无论a取什么实数,图象T与x轴总有公共点.
(2)存在.
当时,.
令,解得,不符合题意.
当时,对于函数,
令,则,
,
或.
,
当或或或时,x为整数,即图象T与x轴的公共点中有整点,
此时或或(舍去)或(舍去)或或或(舍去)或(舍去).
综上可知,整数a的值为0,,1或-2.
20.答案:(1)
(2)
(3) 或或或或
解析:(1)将点,.
代入得,
解得:,
抛物线解析式为:,
(2)与轴交于点A,
当时,
解得:,
,
.
设直线AC的解析式为,
解得:
直线AC的解析式为,
如图所示,过点P作轴于点E,交AC于点Q,
设,则,
,
,,
,
,
,
,
,
当时,PD取得最大值为,,
;
(3)抛物线
将该抛物线向右平移5个单位,得到,对称轴直线,
点向右平移5个单位得到
平移后的抛物线与y轴交于点F,令,则,
,
Q为平移后的抛物线的对称轴上任意一点.
则Q点的横坐标为,
设,
,,
当时,,
解得:或,
当时,,
解得:
当时,,
解得:或 ,
综上所述,Q点的坐标为或或或或.
一、单选题
1.[2023年广西中考真题]将抛物线向右平移3个单位,再向上平移4个单位,得到的抛物线的解析式是( )
A. B.
C. D.
2.[2023年云南中考真题]若点是反比例函数图象上一点,则常数k的值为( )
A.3 B.-3 C. D.
3.[2024年广东中考真题]已知不等式的解集是,则一次函数的图象大致是( )
A. B.
C. D.
4.[2022年青海中考真题]2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )
A. B. C. D.
5.[2024年广东中考真题]若点,,都在二次函数的图象上,则( )
A. B. C. D.
6.[2023年河南中考真题]二次函数的图象如图所示,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.[2023年青海中考真题]生物兴趣小组探究酒精对某种鱼类的心率是否有影响,实验得出心率与酒精浓度的关系如图所示,下列说法正确的是( )
A.酒精浓度越大,心率越高
B.酒精对这种鱼类的心率没有影响
C.当酒精浓度是时,心率是168次/分
D.心率与酒精浓度是反比例函数关系
8.[2024年河南中考真题]把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( )
A.当时,
B.Q随I的增大而增大
C.I每增加1A,Q的增加量相同
D.P越大,插线板电源线产生的热量Q越多
9.[2024年新疆中考真题]如图,在平面直角坐标系中,直线()与双曲线交于A,B两点.轴于点C,连接BC交y轴于点D,结合图象判断下列结论:①点A与点B关于原点对称;②点D是BC的中点;③在的图象上任取点和点,如果,那么;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.[2023年新疆中考真题]如图,在平面直角坐标系中,直线与抛物线相交于点A,B.结合图象,判断下列结论:
①当时,;
②是方程的一个解;
③若,是抛物线上的两点,则;
④对于抛物线,当时,的取值范围是.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
二、填空题
11.[2024年海南中考真题]某型号蓄电池的电压U(单位:V)为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,即,它的图象如图所示,则蓄电池的电压U为__________(V).
12.[2024年辽宁中考真题]如图,在平面直角坐标系中,抛物线与x与相交于点A,B,点B的坐标为,若点在抛物线上,则的长为___________.
13.[2022年安徽中考真题]如图,的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B,若,则________.
14.[2024年新疆中考真题]如图,抛物线与y轴交于点A,与x轴交于点B,线段CD在抛物线的对称轴上移动(点C在点D下方),且.当的值最小时,点C的坐标为__________.
三、解答题
15.[2022年北京中考真题]在平面直角坐标系xOy中,函数的图象经过点,,且与y轴交于点A.
(1)求该函数的解析式及点A的坐标;
(2)当时,对于x的每一个值,函数的值大于函数的值,直接写出n的取值范围.
16.[2023年河南中考真题]小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.
如图,在平面直角坐标系中,点A,C在x轴上,球网AB与y轴的水平距离,,,击球点P在y轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系.
(1)求点P的坐标和a的值.
(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式.
17.[2023年江西中考真题]如图,已知直线与反比例函数的图象交于点,与y轴交于点B,过点B作x轴的平行线交反比例函数的图象于点C.
(1)求直线AB和反比例函数图象的表达式;
(2)求的面积.
18.[2024年新疆中考真题]某公司销售一批产品,经市场调研发现,当销售量在0.4吨至3.5吨之间时,销售额(万元)与销售量x(吨)的函数解析式为:;成本(万元)与销售量x(吨)的函数图象是如图所示的抛物线的一部分,其中是其顶点.
(1)求出成本关于销售量x的函数解析式;
(2)当成本最低时,销售产品所获利润是多少?
(3)当销售量是多少吨时,可获得最大利润?最大利润是多少?
(注:利润=销售额-成本)
19.[2023年云南中考真题]数和形是数学研究客观物体的两个方面.数(代数)侧重研究物体数量方面,具有精确性;形(几何)侧重研究物体形的方面,具有直观性.数和形相互联系,可用数来反映空间形式,也可用形来说明数量关系.数形结合就是把两者结合起来考虑问题,充分利用代数、几何各自的优势,数形互化,共同解决问题.
同学们,请你结合所学的数学解决下列问题.
在平面直角坐标系中,若点的横坐标、纵坐标都为整数,则称这样的点为整点.设函数(实数a为常数)的图象为图象T.
(1)求证:无论a取什么实数,图象T与x轴总有公共点;
(2)是否存在整数a,使图象T与x轴的公共点中有整点?若存在,求所有整数a的值;若不存在,请说明理由.
20.[2023年重庆中考真题]如图,在平面直角坐标系中,抛物线与轴交于点A,,x与y轴交于点C,其中,.
(1)求该抛物线的表达式;
(2)点P是直线AC下方抛物线上一动点,过点P作于点D,求PD的最大值及此时点P的坐标;
(3)在(2)的条件下,将该抛物线向右平移5个单位,点E为点P的对应点,平移后的抛物线与y轴交于点F,Q为平移后的抛物线的对称轴上任意一点.写出所有使得以QF为腰的是等腰三角形的点Q的坐标,并把求其中一个点Q的坐标的过程写出来.
参考答案
1.答案:A
解析:抛物线的顶点坐标是,将点向右平移93个单位,再向上平移4个单位,得到平移后抛物线的顶点坐标为,即.
抛物线开口方向与形状不变,故平移后抛物线的解析式为.
2.答案:A
3.答案:B
解析:A.不等式的解集是,故本选项不符合题意;
B.不等式的解集是,故本选项符合题意;
C.不等式的解集是,故本选项不符合题意;
D.不等式的解集是,故本选项不符合题意;
故选:B.
4.答案:B
解析:随着时间的增多,汽车离剧场的距离y(千米)减少,排除A、C、D;
由于途中停车加油耽误了几分钟,此时时间在增多,汽车离剧场的距离y没有变化;
后来加快了速度,仍保持匀速行进,所以后来的函数图象的走势应比前面匀速前进的走势要陡.故选:B.
5.答案:A
解析:二次函数,
该二次函数的抛物线开口向上,且对称轴为y轴.
当时,y随x的增大而增大,
,
,
故选:A.
6.答案:D
解析:由题图可得,,,的图象经过第一、二、三象限,不经过第四象限.
7.答案:C
解析:由图象可知,酒精浓度越大,心率越低,故A错误;
酒精浓度越大,心率越低,酒精对这种鱼类的心率有影响,故B错误;
由图象可知,当酒精浓度是时,心率是168次/分,故C正确;
任意取两个点坐标,,因为,所以心率与酒精浓度不是反比例函数关系,故D错误.
故选:C.
8.答案:C
解析:由图1可知,当时,,故选项A说法正确,不符合题意;
由图2可知,Q随I的增大而增大,故选项B说法正确,不符合题意;
由图2可知,I每增加1A,Q的增加量不相同故选项C说法错误,符合题意;
由图1可知I随P的增大而增大,由图2可知Q随T的增大而增大,所以P越大,插线板电源线产故选项D说法正确,不符合生的热量Q越多,不符合题意.
故选:C.
9.答案:C
解析:①反比例函数图象与正比例函数图象均关于原点成中心对称,
点A与点B关于原点对称,故①正确;
②点A与点B关于原点对称,.
轴,,是的中位线,
点D是BC的中点,故②正确;
③在每个象限内,y随x的增大而减小,
当P,Q不在同一象限,即点P在第一象限,点Q在第三象限时,;
当P,Q在同一象限时,,故③错误;
④,故④正确.其中正确的结论有①②④,共3个.故选C.
10.答案:B
解析:由图象,得当时,直线上的点位于抛物线上的点的上方,故,因此结论①正确;
由图象,得抛物线经过点,即当时,,故是方程的一个解,因此结论②正确;
将和分别代入,得解得
.
令,得,解得,.
当时,,当时,,则,因此结论③正确;
对于抛物线,若,则当时函数有最大值,最大值为5,
当时函数有最小值,最小值为-4,故的取值范围是,因此结论④错误.
11.答案:64
解析:设用电阻R表示电流I的函数解析式为,
过,
(V),
故答案为:64.
12.答案:4
解析:把点,点代入抛物线得,
,
解得,
抛物线,
令,得,
解得或,
,
;
故答案为:4.
13.答案:3
解析:由题知反比例函数的图象经过点C,设C点坐标为,
作于H,过A点作于G,
如图.四边形OABC是平行四边形,,
,,,
,,即.
的图象经过点B,.
14.答案:
解析:作A点关于对称轴的对称点,向下平移3个单位,得到,连接,交对称轴于点C,此时的值最小,
在中,
令,则,
,
令,则,
解得或,
点,
抛物线的对称轴为直线,
,
,
设直线的解析式为,
代入、B的坐标得,
解得,
直线的解析式为,
当时,,
.
故答案为.
15.答案:(1),
(2)
解析:(1)把,分别代入,
得解得
该函数的解析式为.
对于,当时,,
.
(2).
解法提示:函数的图象如图所示,易知当直线与y轴的交点与点A重合或在点A上方时符合题意,故.
16.答案:(1)-0.4
(2)选择吊球,使球的落地点到C点的距离更近
解析:(1)依题意知,点P为直线与y轴的交点.
当时,,点P的坐标为.
抛物线经过点P,,解得.
(2),,.
若选择扣球,当时,得,解得,
此时,球的落地点到C点的距离为.
若选择吊球,由(1)知,.
当时,得,解得,(舍),
此时球的落地点到C点的距离为.
,应选择吊球.
17.答案:(1)直线AB的表达式为,反比例函数图象的表达式为
(2)
解析:(1)直线与反比例函数的图象交于点,
,,
,,
直线AB的表达式为,反比例函数图象的表达式为.
(2)易得.
轴,
C点的纵坐标为1,BC与x轴的距离为1.
令,得,.
如图,过点A作于点D,
则,
.
18.答案:(1)
(2)
(3)见解析
解析:(1)为抛物线的顶点,
可设抛物线的函数解析式为.
将代入,
得,,
抛物线的函数解析式为.
(2)当时,最小,最小值为万元.
对于,当时,,
此时.
答:成本最低时,所获利润为万元.
(3)设当销售量为x时,利润为w万元.
则.
,
时,w取最大值,最大值是7.
答:当销售量为3吨时,可获得最大利润,最大利润是7万元
19.答案:(1)证明见解析
(2)存在,整数a的值为0,,1或-2
解析:(1),即时,函数的解析式可化为,为一次函数,
当时,图象T与x轴有公共点.
当,即时,函数为二次函数,
,
当时,图象T与x轴总有公共点.
综上可知,无论a取什么实数,图象T与x轴总有公共点.
(2)存在.
当时,.
令,解得,不符合题意.
当时,对于函数,
令,则,
,
或.
,
当或或或时,x为整数,即图象T与x轴的公共点中有整点,
此时或或(舍去)或(舍去)或或或(舍去)或(舍去).
综上可知,整数a的值为0,,1或-2.
20.答案:(1)
(2)
(3) 或或或或
解析:(1)将点,.
代入得,
解得:,
抛物线解析式为:,
(2)与轴交于点A,
当时,
解得:,
,
.
设直线AC的解析式为,
解得:
直线AC的解析式为,
如图所示,过点P作轴于点E,交AC于点Q,
设,则,
,
,,
,
,
,
,
,
当时,PD取得最大值为,,
;
(3)抛物线
将该抛物线向右平移5个单位,得到,对称轴直线,
点向右平移5个单位得到
平移后的抛物线与y轴交于点F,令,则,
,
Q为平移后的抛物线的对称轴上任意一点.
则Q点的横坐标为,
设,
,,
当时,,
解得:或,
当时,,
解得:
当时,,
解得:或 ,
综上所述,Q点的坐标为或或或或.
同课章节目录
