考点五:三角形—三年(2022-2024)中考数学真题分类汇编(含解析)
文档属性
| 名称 | 考点五:三角形—三年(2022-2024)中考数学真题分类汇编(含解析) | 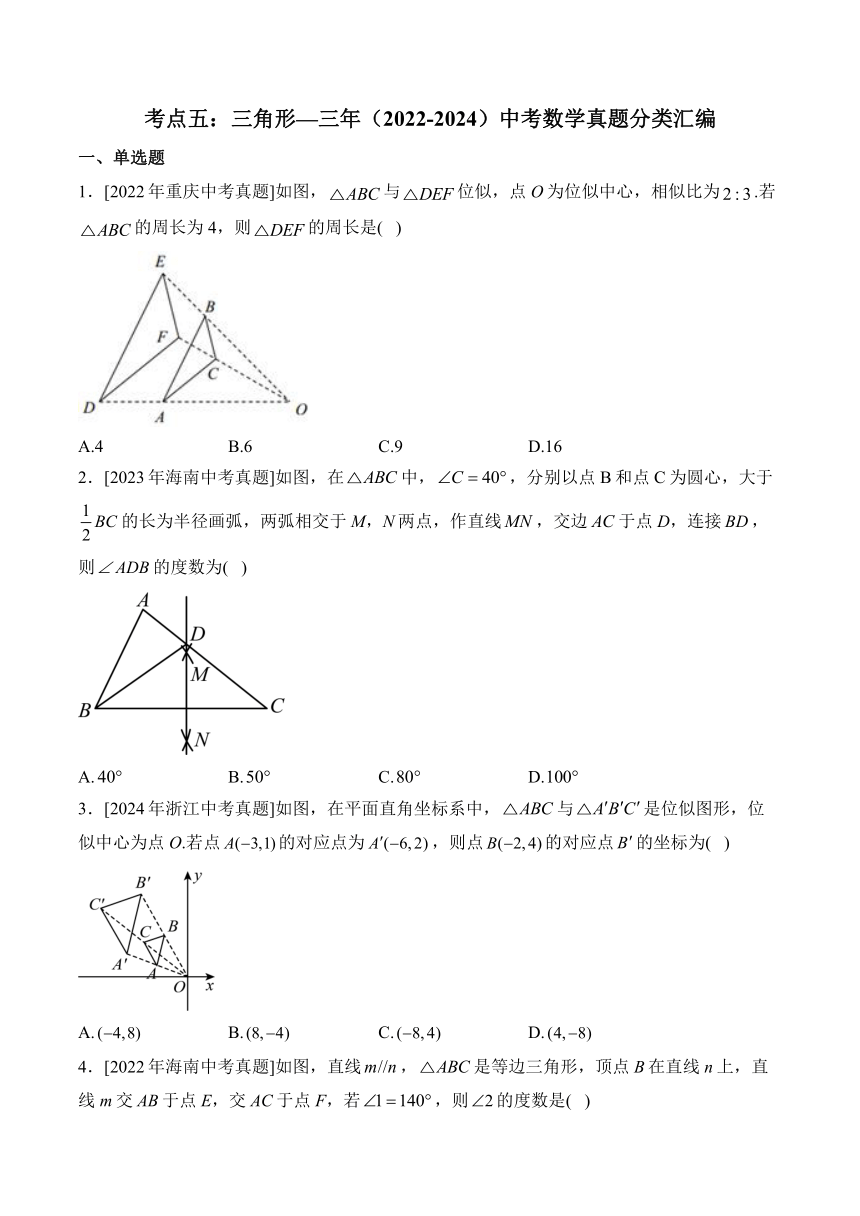 | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 19:02:44 | ||
图片预览



文档简介
考点五:三角形—三年(2022-2024)中考数学真题分类汇编
一、单选题
1.[2022年重庆中考真题]如图,与位似,点O为位似中心,相似比为.若的周长为4,则的周长是( )
A.4 B.6 C.9 D.16
2.[2023年海南中考真题]如图,在中,,分别以点B和点C为圆心,大于的长为半径画弧,两弧相交于M,N两点,作直线,交边于点D,连接,则的度数为( )
A. B. C. D.
3.[2024年浙江中考真题]如图,在平面直角坐标系中,与是位似图形,位似中心为点O.若点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
4.[2022年海南中考真题]如图,直线,是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若,则的度数是( )
A.80° B.100° C.120° D.140°
5.[2022年海南中考真题]如图,在中,,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线BP,交AC于点D,若,则的度数是( )
A.36° B.54° C.72° D.108°
6.[2023年陕西中考真题]如图,是的中位线,点F在上,.连接并延长,与的延长线相交于点M.若,则线段的长为( )
A. B.7 C. D.8
7.[2023年宁夏中考真题]如图,在中,,,.点D在上,且.连接,线段绕点A顺时针旋转得到线段,连接,.则的面积是( )
A. B. C. D.
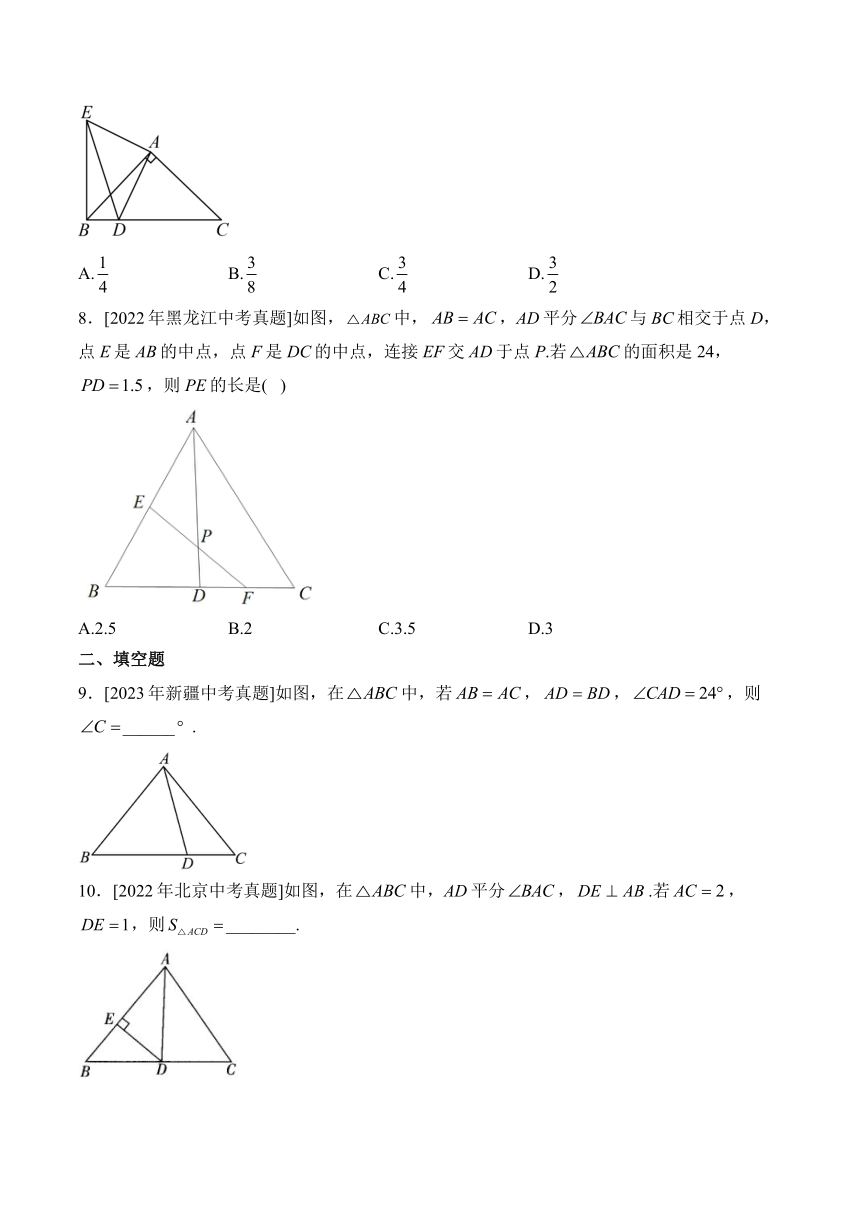
8.[2022年黑龙江中考真题]如图,中,,AD平分与BC相交于点D,点E是AB的中点,点F是DC的中点,连接EF交AD于点P.若的面积是24,,则PE的长是( )
A.2.5 B.2 C.3.5 D.3
二、填空题
9.[2023年新疆中考真题]如图,在中,若,,,则______.
10.[2022年北京中考真题]如图,在中,AD平分,.若,,则________.
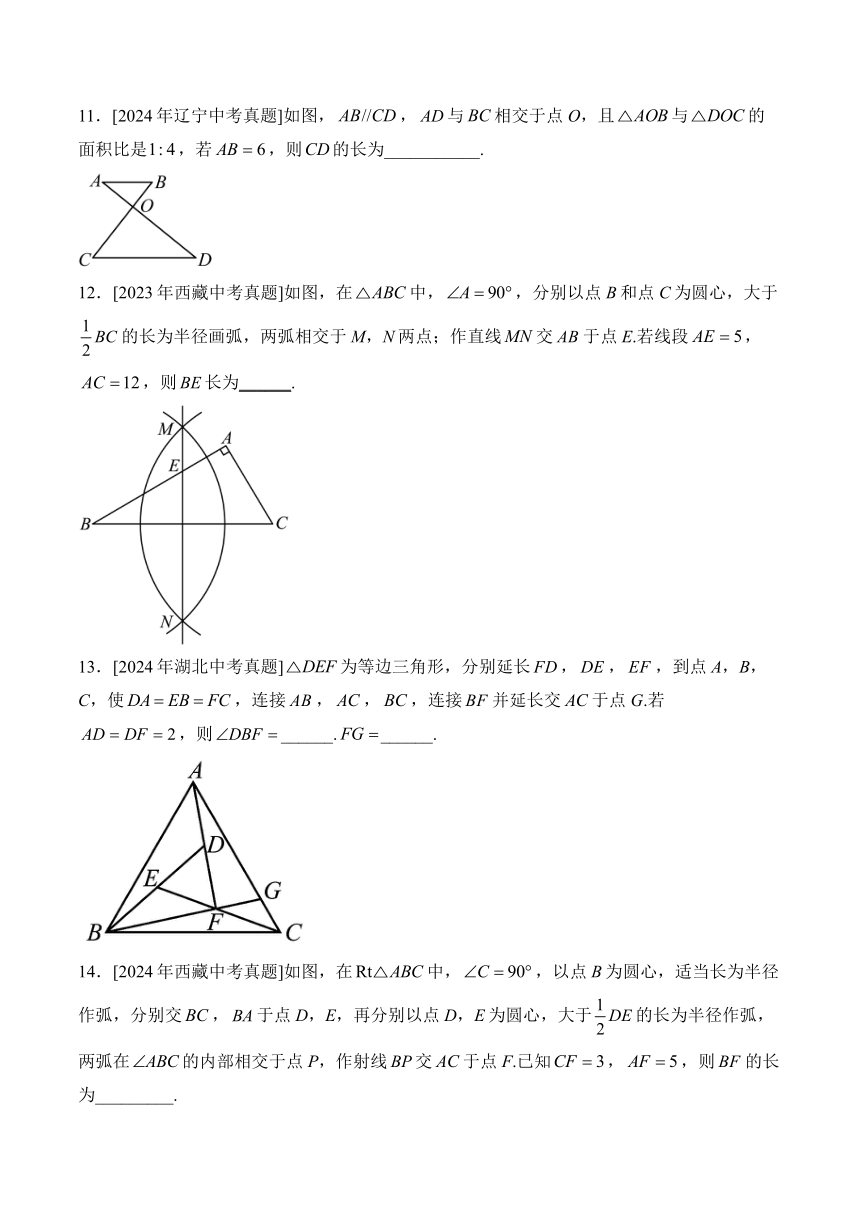
11.[2024年辽宁中考真题]如图,,与相交于点O,且与的面积比是,若,则的长为___________.
12.[2023年西藏中考真题]如图,在中,,分别以点B和点C为圆心,大于的长为半径画弧,两弧相交于M,N两点;作直线交于点E.若线段,,则长为______.
13.[2024年湖北中考真题]为等边三角形,分别延长,,,到点A,B,C,使,连接,,,连接并延长交于点G.若,则______.______.
14.[2024年西藏中考真题]如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为_________.
三、解答题
15.[2024年西藏中考真题]如图,点C是线段的中点,,.求证:.
16.[2023年陕西中考真题]如图,在中,,,过点A作,垂足为E,延长EA至点D,使,在边AC上截取,连接DF.求证:.
17.[2023年西藏中考真题]如图,已知,,.求证:.
18.[2022年上海中考真题]如图所示,在等腰三角形ABC中,,点E,F在线段BC上,点Q在线段AB上,且,.求证:
(1).
(2).
19.[2024年辽宁中考真题]如图,在中,,.将线段绕点C顺时针旋转得到线段,过点D作,垂足为E.
(1)如图1,求证:;
(2)如图2,的平分线与的延长线相交于点F,连接,的延长线与的延长线相交于点P,猜想与的数量关系,并加以证明;
(3)如图3,在(2)的条件下,将沿折叠,在变化过程中,当点P落在点E的位置时,连接.
①求证:点F是的中点;
②若,求的面积.
参考答案
1.答案:B
解析:由两个位似图形的周长比等于位似比可知,,
.故选B.
2.答案:C
解析:由作图可得:为直线的垂直平分线,
,
,
,
故选:C.
3.答案:A
解析:与是位似图形,点的对应点为,
与的位似比为2,
点的对应点的坐标为,即,
故选:A.
4.答案:B
解析:如图,,.
是等边三角形,
,
,.
5.答案:A
解析:由作图可知BD平分∠,
.
,,
,.
在中,,
即,.
6.答案:C
解析:是的中位线,
,,
,
,
,
.
故选:C.
7.答案:B
解析:线段绕点A顺时针旋转得到线段,
,,
,
在中,,,
,,
,
,
,,
,
,,
,,
,
故选:B.
8.答案:A
解析:如图,过点E作于G,
,AD平分,
,,
,,
点E是AB的中点,
G是AD的中点,
,
F是CD的中点,
,
,
,
,
,
,
的面积是24,
,
,
,
,
由勾股定理得:.
故选:A.
9.答案:52
解析:,,
.
,.
10.答案:1
解析:如图,过点D作于点F.
平分,,,
.
11.答案:12
解析:,
,
,
,
,
故答案为:12.
12.答案:13
解析:连接,如图,
根据作图可知:是线段的垂直平分线,
,
,,,
在中,,
,
故答案为:13.
13.答案:;
解析:为等边三角形,,
,,
,,,
作交的延长线于点H,
,,
,
,
,
,即,
解得,
故答案为:,.
14.答案:
解析:过F作于G,
由作图得:平分,,,
∴,
在中根据勾股定理得:,
,,
,
,
设,则,,
在中,根据勾股定理得:
,
即:,
解得:,
,
在中根据勾股定理得:.
故答案为:.
15.答案:见解析
解析:证明:∵点C是线段的中点,
∴,
在和中,
,
∴,
∴.
16.答案:见解析
解析:证明:在中,,,
.
,.,
.
又,,,
.
17.答案:见解析
解析:证明:在和中,
,
,
,
,
.
18.答案:(1)证明见解析
(2)证明见解析
解析:(1),,
,,即.
在和中,
,.
(2)由(1)知,
,
,,,,
又,
,,
,
,,
,
,,
,.
19.答案:(1)见详解
(2)
(3)30
解析:(1)证明:如图,
由题意得,,,
,
,
,
,
,
,
;
(2)猜想:,
证明:,,
,
平分,
,
,,
,
,
,,
,
,
;
(3)①由题意得,
,
,
,
,,
,
,
,即点F是中点;
②过点F作交于点M,连接,
,
,
设,,
,
由翻折得,
,
,
在中,由勾股定理得:,
整理得,,
解得:或(舍,此时),
在中,由勾股定理得:,
解得:,
,
,
,,
点M为中点,
,
.
一、单选题
1.[2022年重庆中考真题]如图,与位似,点O为位似中心,相似比为.若的周长为4,则的周长是( )
A.4 B.6 C.9 D.16
2.[2023年海南中考真题]如图,在中,,分别以点B和点C为圆心,大于的长为半径画弧,两弧相交于M,N两点,作直线,交边于点D,连接,则的度数为( )
A. B. C. D.
3.[2024年浙江中考真题]如图,在平面直角坐标系中,与是位似图形,位似中心为点O.若点的对应点为,则点的对应点的坐标为( )
A. B. C. D.
4.[2022年海南中考真题]如图,直线,是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若,则的度数是( )
A.80° B.100° C.120° D.140°
5.[2022年海南中考真题]如图,在中,,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线BP,交AC于点D,若,则的度数是( )
A.36° B.54° C.72° D.108°
6.[2023年陕西中考真题]如图,是的中位线,点F在上,.连接并延长,与的延长线相交于点M.若,则线段的长为( )
A. B.7 C. D.8
7.[2023年宁夏中考真题]如图,在中,,,.点D在上,且.连接,线段绕点A顺时针旋转得到线段,连接,.则的面积是( )
A. B. C. D.
8.[2022年黑龙江中考真题]如图,中,,AD平分与BC相交于点D,点E是AB的中点,点F是DC的中点,连接EF交AD于点P.若的面积是24,,则PE的长是( )
A.2.5 B.2 C.3.5 D.3
二、填空题
9.[2023年新疆中考真题]如图,在中,若,,,则______.
10.[2022年北京中考真题]如图,在中,AD平分,.若,,则________.
11.[2024年辽宁中考真题]如图,,与相交于点O,且与的面积比是,若,则的长为___________.
12.[2023年西藏中考真题]如图,在中,,分别以点B和点C为圆心,大于的长为半径画弧,两弧相交于M,N两点;作直线交于点E.若线段,,则长为______.
13.[2024年湖北中考真题]为等边三角形,分别延长,,,到点A,B,C,使,连接,,,连接并延长交于点G.若,则______.______.
14.[2024年西藏中考真题]如图,在中,,以点B为圆心,适当长为半径作弧,分别交,于点D,E,再分别以点D,E为圆心,大于的长为半径作弧,两弧在的内部相交于点P,作射线交于点F.已知,,则的长为_________.
三、解答题
15.[2024年西藏中考真题]如图,点C是线段的中点,,.求证:.
16.[2023年陕西中考真题]如图,在中,,,过点A作,垂足为E,延长EA至点D,使,在边AC上截取,连接DF.求证:.
17.[2023年西藏中考真题]如图,已知,,.求证:.
18.[2022年上海中考真题]如图所示,在等腰三角形ABC中,,点E,F在线段BC上,点Q在线段AB上,且,.求证:
(1).
(2).
19.[2024年辽宁中考真题]如图,在中,,.将线段绕点C顺时针旋转得到线段,过点D作,垂足为E.
(1)如图1,求证:;
(2)如图2,的平分线与的延长线相交于点F,连接,的延长线与的延长线相交于点P,猜想与的数量关系,并加以证明;
(3)如图3,在(2)的条件下,将沿折叠,在变化过程中,当点P落在点E的位置时,连接.
①求证:点F是的中点;
②若,求的面积.
参考答案
1.答案:B
解析:由两个位似图形的周长比等于位似比可知,,
.故选B.
2.答案:C
解析:由作图可得:为直线的垂直平分线,
,
,
,
故选:C.
3.答案:A
解析:与是位似图形,点的对应点为,
与的位似比为2,
点的对应点的坐标为,即,
故选:A.
4.答案:B
解析:如图,,.
是等边三角形,
,
,.
5.答案:A
解析:由作图可知BD平分∠,
.
,,
,.
在中,,
即,.
6.答案:C
解析:是的中位线,
,,
,
,
,
.
故选:C.
7.答案:B
解析:线段绕点A顺时针旋转得到线段,
,,
,
在中,,,
,,
,
,
,,
,
,,
,,
,
故选:B.
8.答案:A
解析:如图,过点E作于G,
,AD平分,
,,
,,
点E是AB的中点,
G是AD的中点,
,
F是CD的中点,
,
,
,
,
,
,
的面积是24,
,
,
,
,
由勾股定理得:.
故选:A.
9.答案:52
解析:,,
.
,.
10.答案:1
解析:如图,过点D作于点F.
平分,,,
.
11.答案:12
解析:,
,
,
,
,
故答案为:12.
12.答案:13
解析:连接,如图,
根据作图可知:是线段的垂直平分线,
,
,,,
在中,,
,
故答案为:13.
13.答案:;
解析:为等边三角形,,
,,
,,,
作交的延长线于点H,
,,
,
,
,
,即,
解得,
故答案为:,.
14.答案:
解析:过F作于G,
由作图得:平分,,,
∴,
在中根据勾股定理得:,
,,
,
,
设,则,,
在中,根据勾股定理得:
,
即:,
解得:,
,
在中根据勾股定理得:.
故答案为:.
15.答案:见解析
解析:证明:∵点C是线段的中点,
∴,
在和中,
,
∴,
∴.
16.答案:见解析
解析:证明:在中,,,
.
,.,
.
又,,,
.
17.答案:见解析
解析:证明:在和中,
,
,
,
,
.
18.答案:(1)证明见解析
(2)证明见解析
解析:(1),,
,,即.
在和中,
,.
(2)由(1)知,
,
,,,,
又,
,,
,
,,
,
,,
,.
19.答案:(1)见详解
(2)
(3)30
解析:(1)证明:如图,
由题意得,,,
,
,
,
,
,
,
;
(2)猜想:,
证明:,,
,
平分,
,
,,
,
,
,,
,
,
;
(3)①由题意得,
,
,
,
,,
,
,
,即点F是中点;
②过点F作交于点M,连接,
,
,
设,,
,
由翻折得,
,
,
在中,由勾股定理得:,
整理得,,
解得:或(舍,此时),
在中,由勾股定理得:,
解得:,
,
,
,,
点M为中点,
,
.
同课章节目录
