2.5角和角的度量 课件(共31张PPT)-七年级数学上册考试满分全攻略备课备考系列(冀教版2024)
文档属性
| 名称 | 2.5角和角的度量 课件(共31张PPT)-七年级数学上册考试满分全攻略备课备考系列(冀教版2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 19:26:51 | ||
图片预览











文档简介
(共31张PPT)
冀教版(2024)七年级数学上册 第二章 几何图形的初步认识
2.5 角和角的度量
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.通过丰富是实例和画角,抽象出角,感知角的构成,
进一步认识角及角的意义,了解角的表示方法
2.认识角的度量单位:度、分、秒,会进行角度的换算.
情景导入
角在生中
无处不在
新知探究
下面左图是人站在地面上看大楼的底部和顶部的视线示意图,右图是停车场出入口的栏杆由下向上转动的示意图.你能指出图中的角吗 这些角是怎样形成的.
从上面的图中可以得到图2.5-1所示的几何图形.
解:左图是从视点看大楼的视角,两条视线可以看成从同一点出发的两条射线.
右图是道口栏杆旋转,可以看成一条射线绕着一个点逆时针旋转.
有公共端点的两条射线所组成的图形叫作角,这个公共端点叫作角的顶点,这两条射线叫作角的边.如图2.5-1,点O是角的顶点,射线OA 和OB是角的边.
角也可以看作是一条射线绕着其端点从一个位置旋转到另一个位置所形成的图形.起始位置的射线叫作角的始边,终止位置的射线叫作角的终边. 通常用符号 “∠”表示角,具体表示方法如图2.5-2所示.
在不作特别说明 的情况下,初中阶段 我们说的角都是小于 平角的角.
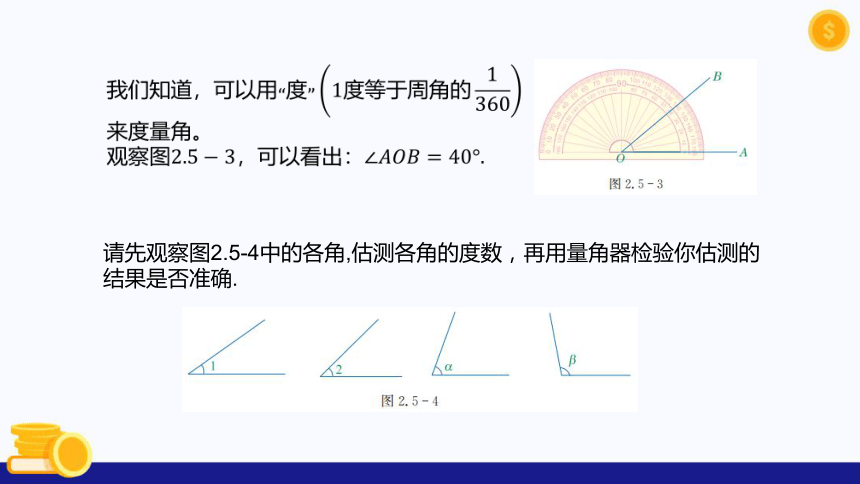
请先观察图2.5-4中的各角,估测各角的度数,再用量角器检验你估测的结果是否准确.
为了更精细地度量角,我们引入更小的角的度量单位:分、秒.把1°的角等分成60份,每份叫作1分的角,1分记作1 ′ ;把1 ′的角再等分成60份, 每份叫作1秒的角,1秒记作1″.角的度、分、秒是60进制的,这和计量时间的时、分、秒进制是一样的.
概念归纳
有公共端点的两条射线所组成的图形叫作角,这个公共端点叫作角的顶点,这两条射线叫作角的边.
课本例题
例1 将57.32°用度、分、秒表示.
解:先把0.32°化成分,
0.32°=60′×0.32=19.2′.
再把0.2′化成秒,
0.2′=60″×0.2=12″.
所以57.23°=57°19′12″.
课本例题
例2 将10°6′36" 用度表示
先把36″化为分,
36″=( )′×36=0.6′
6′+0.6′=6.6′
再把6.6′化为度,
6.6′=()°×6.6=0.11°
所以10°6′36″=10.11°
解:
课堂练习
1.请写出下列各图中的角:
2.填空:
(1)1周角= 平角,1平角= 直角,1直角= °,
1°= ’,1’= ″.
(2)经过1h,钟表的时针转过的角度是 ,分针转过的角度是 ;经过15min,分针转过的角度是 ,时针转过的角度是 .
60
60
90
2
2
7.5°
90°
30°
360°
分层练习-基础
知识点1 角及有关角的定义
1. [新考法·定义辨析法]下列说法中,正确的是( B )
A. 两条射线所组成的图形叫作角
B. 角的大小与所画角的两边的长短无关
C. 角的两边是两条线段
D. 角的两边是两条直线
B
2. 已知, O 为直线 AB 上的一点,画出射线 OC (如图①),则
图中有 个角(除平角外);再画出射线 OD (如图②),
则图中有 个角(除平角外);再画出射线 OE (如图
③),则图中有 个角(除平角外).
2
5
9
知识点2 角的表示方法
3. 如图,下列各个图形中,能用∠1,∠ AOB ,∠ O 三种方
法表示同一角的图形是( B )
B
4. 下列对于图形的描述中,正确的有( B )
A. 1个 B. 2个
第1个图形是以 A 为顶点的角,应表示为∠ CAB 或∠ A ,故错误;根据周角与平角的定义可知,对第2,3个图形的描述正确,第4个图形的描述错误.故正确的有2个,故选B.
【点拨】
B
【答案】
C. 3个 D. 4个
知识点3 角的度量
5. [母题 教材P81习题B组T4]请用度表示:74°19'30″
= .
【点拨】
因为30″=0.5',19.5'=0.325°,
所以74°19'30″=74.325°.
74.325°
6. [2023·临沂]如图中用量角器测得∠ ABC 的度数是( C )
A. 50° B. 80°
C. 130° D. 150°
C
7. 下面等式中,角度互化成立的是( D )
A. 83.5°=83°5'
B. 37°12'36″=37.48°
C. 24°24'24″=24.44°
D. 41.25°=41°15'
C. 24″=0.4',24.4'≈0.41°,所以24°24'24″≈24.41°,故C错误;
D. 0.25°=15',所以41.25°=41°15',故D正确.
【点拨】
A. 0.5°=30',所以83.5°=83°30',故A错误;
B. 36″=0.6',12.6'=0.21°,所以37°12'36″=37.21°,故B错误;
【答案】
D
知识点4 钟面角
8. [情境题·生活应用]如图,分别确定四个城市相应钟表上时
针与分针所成的角的度数,填在钟表下方的横线上.
9. [新考法·分类讨论法]当分针指向12,时针这时恰好与分针
成120°的角,此时是( D )
A. 9点钟 B. 8点钟
C. 4点钟 D. 8点钟或4点钟
【点拨】
当分针指向12,与时针的夹角为120°时,有如图两种情况,此时是8点钟或4点钟,故选D.
D
10. 某一时刻,时钟上显示的时间是9点30分,则此时时针与
分针的夹角是( C )
A. 75° B. 90°
C. 105° D. 120°
【点拨】
当时间是9点30分时,时钟如图所示,此
时时针与分针的夹角为90°+15°=105°,
故选C.
C
易错点 度、分、秒转化时,误按十进制进行换算
11. (1)把26.19°转化为用度、分、秒表示
为 ;
(2)把33°14'24″转化为用度表示为 .
26°11'24″
33.24°
分层练习-巩固
利用角的定义及度量画符合条件的角
12. 根据下列语句画图:
(1)画∠ AOB =100°;
(2)在∠ AOB 的内部画射线 OC ,使∠ BOC =50°;
(3)在∠ AOB 的外部画射线 OD ,使∠ DOA =40°;
(4)在射线 OD 上取点 E ,在射线 OA 上取点 F ,使∠ OEF =90°.
【解】(1)~(4)如图所示.
利用角度解决实际问题
13. [2024·长沙明德中学模拟]魏老师去市场买菜,他发现若把5 kg的菜放到秤上,指针盘上的指针转了180°.
(1)如果把0.5 kg的菜放在秤上,求指针转过的角度;
【解】 ×0.5=18°.
故把0.5 kg的菜放在秤上,指针转过的角度是18°.
(2)如果指针转了270°,那么这些菜有多少千克?
【解】270°÷ =7.5(kg). 故这些菜有7.5 kg.
分层练习-拓展
利用钟面上角的特征探究时针与分针夹角的度数
14. [新考向·身边的数学]钟表的时针和分针如同兄弟俩在赛
跑,其中蕴涵着丰富的数学知识.
(1)如图①,8:00这一时刻,时钟上分针与时针的夹角
等于 .
120°
(2)请在图②中画出8:20这一时刻时针和分针的大致位置,思考并回答:从上午8:00到8:20,时钟的分针转过的度数是 ,时钟的时针转过的度数是 .
120°
10°
【解】8:20这一时刻时针和分针的大致位置如图
所示.
(3)“元旦”这一天,小明上午8:00出门买东西,回到家中时发现还没到9:00,但是时针与分针重合了,那么小明从离开家到回到家的时间为多少分钟?
【解】设小明从离开家到回到家的时间为 x 分钟,
因为8:00时,时针与分针的夹角为120°,到家时,
时针与分针重合,即分针比时针多走了240°,
所以6 x -0. 5 x =240,解得 x = ,
即小明从离开家到回到家的时间为 分钟.
课堂小结
角
角的定义及表示方法
角的度量与换算
角的定义:有公共端点的两条射线所组成的图形,叫作角.
角的表示方法
角的度量工具:量角器
角的换算
1周角=360°;1平角=180°
1°=60′;1′=60″.
冀教版(2024)七年级数学上册 第二章 几何图形的初步认识
2.5 角和角的度量
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.通过丰富是实例和画角,抽象出角,感知角的构成,
进一步认识角及角的意义,了解角的表示方法
2.认识角的度量单位:度、分、秒,会进行角度的换算.
情景导入
角在生中
无处不在
新知探究
下面左图是人站在地面上看大楼的底部和顶部的视线示意图,右图是停车场出入口的栏杆由下向上转动的示意图.你能指出图中的角吗 这些角是怎样形成的.
从上面的图中可以得到图2.5-1所示的几何图形.
解:左图是从视点看大楼的视角,两条视线可以看成从同一点出发的两条射线.
右图是道口栏杆旋转,可以看成一条射线绕着一个点逆时针旋转.
有公共端点的两条射线所组成的图形叫作角,这个公共端点叫作角的顶点,这两条射线叫作角的边.如图2.5-1,点O是角的顶点,射线OA 和OB是角的边.
角也可以看作是一条射线绕着其端点从一个位置旋转到另一个位置所形成的图形.起始位置的射线叫作角的始边,终止位置的射线叫作角的终边. 通常用符号 “∠”表示角,具体表示方法如图2.5-2所示.
在不作特别说明 的情况下,初中阶段 我们说的角都是小于 平角的角.
请先观察图2.5-4中的各角,估测各角的度数,再用量角器检验你估测的结果是否准确.
为了更精细地度量角,我们引入更小的角的度量单位:分、秒.把1°的角等分成60份,每份叫作1分的角,1分记作1 ′ ;把1 ′的角再等分成60份, 每份叫作1秒的角,1秒记作1″.角的度、分、秒是60进制的,这和计量时间的时、分、秒进制是一样的.
概念归纳
有公共端点的两条射线所组成的图形叫作角,这个公共端点叫作角的顶点,这两条射线叫作角的边.
课本例题
例1 将57.32°用度、分、秒表示.
解:先把0.32°化成分,
0.32°=60′×0.32=19.2′.
再把0.2′化成秒,
0.2′=60″×0.2=12″.
所以57.23°=57°19′12″.
课本例题
例2 将10°6′36" 用度表示
先把36″化为分,
36″=( )′×36=0.6′
6′+0.6′=6.6′
再把6.6′化为度,
6.6′=()°×6.6=0.11°
所以10°6′36″=10.11°
解:
课堂练习
1.请写出下列各图中的角:
2.填空:
(1)1周角= 平角,1平角= 直角,1直角= °,
1°= ’,1’= ″.
(2)经过1h,钟表的时针转过的角度是 ,分针转过的角度是 ;经过15min,分针转过的角度是 ,时针转过的角度是 .
60
60
90
2
2
7.5°
90°
30°
360°
分层练习-基础
知识点1 角及有关角的定义
1. [新考法·定义辨析法]下列说法中,正确的是( B )
A. 两条射线所组成的图形叫作角
B. 角的大小与所画角的两边的长短无关
C. 角的两边是两条线段
D. 角的两边是两条直线
B
2. 已知, O 为直线 AB 上的一点,画出射线 OC (如图①),则
图中有 个角(除平角外);再画出射线 OD (如图②),
则图中有 个角(除平角外);再画出射线 OE (如图
③),则图中有 个角(除平角外).
2
5
9
知识点2 角的表示方法
3. 如图,下列各个图形中,能用∠1,∠ AOB ,∠ O 三种方
法表示同一角的图形是( B )
B
4. 下列对于图形的描述中,正确的有( B )
A. 1个 B. 2个
第1个图形是以 A 为顶点的角,应表示为∠ CAB 或∠ A ,故错误;根据周角与平角的定义可知,对第2,3个图形的描述正确,第4个图形的描述错误.故正确的有2个,故选B.
【点拨】
B
【答案】
C. 3个 D. 4个
知识点3 角的度量
5. [母题 教材P81习题B组T4]请用度表示:74°19'30″
= .
【点拨】
因为30″=0.5',19.5'=0.325°,
所以74°19'30″=74.325°.
74.325°
6. [2023·临沂]如图中用量角器测得∠ ABC 的度数是( C )
A. 50° B. 80°
C. 130° D. 150°
C
7. 下面等式中,角度互化成立的是( D )
A. 83.5°=83°5'
B. 37°12'36″=37.48°
C. 24°24'24″=24.44°
D. 41.25°=41°15'
C. 24″=0.4',24.4'≈0.41°,所以24°24'24″≈24.41°,故C错误;
D. 0.25°=15',所以41.25°=41°15',故D正确.
【点拨】
A. 0.5°=30',所以83.5°=83°30',故A错误;
B. 36″=0.6',12.6'=0.21°,所以37°12'36″=37.21°,故B错误;
【答案】
D
知识点4 钟面角
8. [情境题·生活应用]如图,分别确定四个城市相应钟表上时
针与分针所成的角的度数,填在钟表下方的横线上.
9. [新考法·分类讨论法]当分针指向12,时针这时恰好与分针
成120°的角,此时是( D )
A. 9点钟 B. 8点钟
C. 4点钟 D. 8点钟或4点钟
【点拨】
当分针指向12,与时针的夹角为120°时,有如图两种情况,此时是8点钟或4点钟,故选D.
D
10. 某一时刻,时钟上显示的时间是9点30分,则此时时针与
分针的夹角是( C )
A. 75° B. 90°
C. 105° D. 120°
【点拨】
当时间是9点30分时,时钟如图所示,此
时时针与分针的夹角为90°+15°=105°,
故选C.
C
易错点 度、分、秒转化时,误按十进制进行换算
11. (1)把26.19°转化为用度、分、秒表示
为 ;
(2)把33°14'24″转化为用度表示为 .
26°11'24″
33.24°
分层练习-巩固
利用角的定义及度量画符合条件的角
12. 根据下列语句画图:
(1)画∠ AOB =100°;
(2)在∠ AOB 的内部画射线 OC ,使∠ BOC =50°;
(3)在∠ AOB 的外部画射线 OD ,使∠ DOA =40°;
(4)在射线 OD 上取点 E ,在射线 OA 上取点 F ,使∠ OEF =90°.
【解】(1)~(4)如图所示.
利用角度解决实际问题
13. [2024·长沙明德中学模拟]魏老师去市场买菜,他发现若把5 kg的菜放到秤上,指针盘上的指针转了180°.
(1)如果把0.5 kg的菜放在秤上,求指针转过的角度;
【解】 ×0.5=18°.
故把0.5 kg的菜放在秤上,指针转过的角度是18°.
(2)如果指针转了270°,那么这些菜有多少千克?
【解】270°÷ =7.5(kg). 故这些菜有7.5 kg.
分层练习-拓展
利用钟面上角的特征探究时针与分针夹角的度数
14. [新考向·身边的数学]钟表的时针和分针如同兄弟俩在赛
跑,其中蕴涵着丰富的数学知识.
(1)如图①,8:00这一时刻,时钟上分针与时针的夹角
等于 .
120°
(2)请在图②中画出8:20这一时刻时针和分针的大致位置,思考并回答:从上午8:00到8:20,时钟的分针转过的度数是 ,时钟的时针转过的度数是 .
120°
10°
【解】8:20这一时刻时针和分针的大致位置如图
所示.
(3)“元旦”这一天,小明上午8:00出门买东西,回到家中时发现还没到9:00,但是时针与分针重合了,那么小明从离开家到回到家的时间为多少分钟?
【解】设小明从离开家到回到家的时间为 x 分钟,
因为8:00时,时针与分针的夹角为120°,到家时,
时针与分针重合,即分针比时针多走了240°,
所以6 x -0. 5 x =240,解得 x = ,
即小明从离开家到回到家的时间为 分钟.
课堂小结
角
角的定义及表示方法
角的度量与换算
角的定义:有公共端点的两条射线所组成的图形,叫作角.
角的表示方法
角的度量工具:量角器
角的换算
1周角=360°;1平角=180°
1°=60′;1′=60″.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
