3.1.2圆柱的表面积 课件(共17张PPT)-六年级数学上册精品课堂(人教版五四制2024)
文档属性
| 名称 | 3.1.2圆柱的表面积 课件(共17张PPT)-六年级数学上册精品课堂(人教版五四制2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
3.1.2 圆柱的表面积
主讲:
人教版(五四制2024)六年级数学上册
第三章 圆柱与圆锥
学习目标
1.通过想像、操作等活动,使学生知道圆柱侧面展开后是一个长方形,加深对圆柱特征的认识,发展空间观念。
2.结合具体情境和动手操作,探索圆柱侧面积的计算方法“化曲面为平面”,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
3.让学生体验出自己探究发现的快乐。感受到数学与日常生活联系广泛,激发起热爱数学的情感。
目标
1
目标
2
目标
3
新课引入
两个底面
一个侧面
完全重合的两个圆面
曲面
高
两底面之间的距离
回忆圆柱的特征
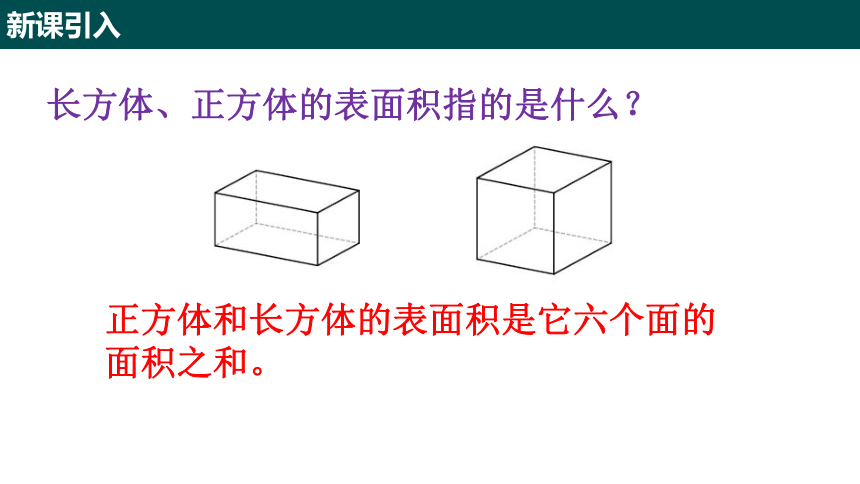
长方体、正方体的表面积指的是什么?
正方体和长方体的表面积是它六个面的面积之和。
新课引入
长方体、正方体的表面积公式
新课引入
圆柱的表面积等于........
两个圆面的面积+一个侧面的面积
新知讲授
r
2
新知讲授
探究
将一个圆柱展开,你能得到什么图形?
它的侧面展开图是什么形状?
侧面展开图的各部分与圆柱的底面、高有什么关系?
动手试一试
并回答问题
归纳
将一个圆柱沿垂直于底面的方向展开,可以能得到两个大小相同的圆面,侧面展开是一个长方形.
沿圆柱的高线展开
围底面一周
侧面展开长方形的长等于底面圆的周长,宽等于圆柱的高
新知讲授
r
h
圆柱的表面积等于........
圆柱的表面积=
侧面积
+两个底面积
长方形的面积
底面周长×高
+2×圆面积
2×h
+2
圆柱的表面积=
圆柱的表面积=
新知讲授
r
h
如果圆柱的底面半径是r,高是h,则
圆柱的侧面积=2πrh
圆柱的表面积=2πrh+2πr2
新知讲授
课堂例题
例1 一顶厨师帽近似圆柱形,高约是30cm,帽顶直径是20cm.做这样一顶帽子大约需要用多少平方厘米的面料(结果保留整十数)
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
想一想:这个帽子是什么样的,它由哪几面组成?
课堂例题
例1 一顶厨师帽近似圆柱形,高约是30cm,帽顶直径是20cm.做这样一顶帽子大约需要用多少平方厘米的面料(结果保留整十数)
解:帽子的侧面积为
3.14×20×30=1884(cm )
帽顶的面积为
3.14×(20÷2) =314(cm );
因此,做这样一顶帽子大约需要用的面料为
1884+314=2198≈2200(cm ).
说一说:你学会了什么?
小结
课堂练习
1.计算下面圆柱的表面积。(单位:cm)
2.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动一周,压路面积是多少平方米?
分析:求压路机前轮转动一周,压路的面积,也就是求前轮圆柱形的侧面面积。
3.14×1.2×2 = 7.536(m2)
答:压路的面积为7.536m2
课堂练习
课堂小结
这节课你学到了什么,有什么收获?
说一说
实际问题还要根据具体情况计算表面积涉及哪几个面。
主讲:
感谢聆听
人教版(五四制2024)六年级数学上册
3.1.2 圆柱的表面积
主讲:
人教版(五四制2024)六年级数学上册
第三章 圆柱与圆锥
学习目标
1.通过想像、操作等活动,使学生知道圆柱侧面展开后是一个长方形,加深对圆柱特征的认识,发展空间观念。
2.结合具体情境和动手操作,探索圆柱侧面积的计算方法“化曲面为平面”,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
3.让学生体验出自己探究发现的快乐。感受到数学与日常生活联系广泛,激发起热爱数学的情感。
目标
1
目标
2
目标
3
新课引入
两个底面
一个侧面
完全重合的两个圆面
曲面
高
两底面之间的距离
回忆圆柱的特征
长方体、正方体的表面积指的是什么?
正方体和长方体的表面积是它六个面的面积之和。
新课引入
长方体、正方体的表面积公式
新课引入
圆柱的表面积等于........
两个圆面的面积+一个侧面的面积
新知讲授
r
2
新知讲授
探究
将一个圆柱展开,你能得到什么图形?
它的侧面展开图是什么形状?
侧面展开图的各部分与圆柱的底面、高有什么关系?
动手试一试
并回答问题
归纳
将一个圆柱沿垂直于底面的方向展开,可以能得到两个大小相同的圆面,侧面展开是一个长方形.
沿圆柱的高线展开
围底面一周
侧面展开长方形的长等于底面圆的周长,宽等于圆柱的高
新知讲授
r
h
圆柱的表面积等于........
圆柱的表面积=
侧面积
+两个底面积
长方形的面积
底面周长×高
+2×圆面积
2×h
+2
圆柱的表面积=
圆柱的表面积=
新知讲授
r
h
如果圆柱的底面半径是r,高是h,则
圆柱的侧面积=2πrh
圆柱的表面积=2πrh+2πr2
新知讲授
课堂例题
例1 一顶厨师帽近似圆柱形,高约是30cm,帽顶直径是20cm.做这样一顶帽子大约需要用多少平方厘米的面料(结果保留整十数)
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
想一想:这个帽子是什么样的,它由哪几面组成?
课堂例题
例1 一顶厨师帽近似圆柱形,高约是30cm,帽顶直径是20cm.做这样一顶帽子大约需要用多少平方厘米的面料(结果保留整十数)
解:帽子的侧面积为
3.14×20×30=1884(cm )
帽顶的面积为
3.14×(20÷2) =314(cm );
因此,做这样一顶帽子大约需要用的面料为
1884+314=2198≈2200(cm ).
说一说:你学会了什么?
小结
课堂练习
1.计算下面圆柱的表面积。(单位:cm)
2.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动一周,压路面积是多少平方米?
分析:求压路机前轮转动一周,压路的面积,也就是求前轮圆柱形的侧面面积。
3.14×1.2×2 = 7.536(m2)
答:压路的面积为7.536m2
课堂练习
课堂小结
这节课你学到了什么,有什么收获?
说一说
实际问题还要根据具体情况计算表面积涉及哪几个面。
主讲:
感谢聆听
人教版(五四制2024)六年级数学上册
同课章节目录
