3.6二次函数的应用(第1课时)课件(共24张PPT)-九年级数学上册精品课堂(鲁教版五四制)
文档属性
| 名称 | 3.6二次函数的应用(第1课时)课件(共24张PPT)-九年级数学上册精品课堂(鲁教版五四制) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
3.6 二次函数的应用
第三章 二次函数
第一课时
教学目标
1
2
3
1、.经历探究几何图形中的最值问题,学会用二次函数来解决几何图形中最值问题.体会二次函数的应用意义以及数学的转化思想.
2、通过自主探究,理解二次函数的应用.经过合作交流,了解二次函数解决几何图形最值问题的基本思路,提高学生的分析总结能力.
3、通过几何图形中的最值问题的探究活动,建立学生对二次函数应用的以及数形结合的思维,培养学生勇于探索的学习习惯.
知识回顾
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
二次函数的性质与解析式系数的关系
当x=-=,
y最小值= =-
知识回顾
二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值?
a>0
a<0
当x=-,函数值有最大值,y最大值=
当x=-,函数值有最大值,y最小值=
1、求下列函数的最大值或最小值:
①y=x2-4x+7 ②y=-5x2+8x-1
配方法
公式法
练一练
选择合适的方法
①y=x2-4x+7
=(x-2)2+3
当x=2时,y最小值=3
练一练
知识回顾
2.二次函数y=ax2+bx+c,b2=ac,且x=0时y=-4,则( )
A 、y最大=-4 B、y最小=-4 C、y最大=-3 D、y最小=3
把x=0,y=-4代入得:
c=-4
∵b2=ac>0
∴a<0
解析:
∴抛物线开口向下,函数有最大值
∴y最大值= = =-3
C
新知导入
何 时 面 积 最 大
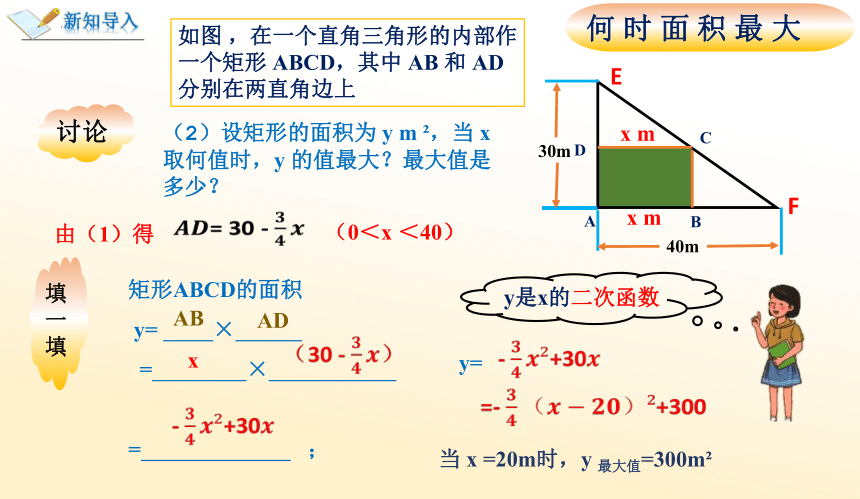
如图 ,在一个直角三角形的内部作一个矩形 ABCD,其中 AB 和 AD 分别在两直角边上
D
A
B
C
40m
30m
(1)如果设矩形的一边 AB = x m,那么 AD边的长度如何表示?
讨论
x m
E
F
如图
∵AF∥DC
∴△AFE∽△DCE
∴ =
x m
∴ =
∵四边形ABCD矩形
∴AB=DC=Xm
∴ = 30 -
x的取值范围是什么?
0<x <40
新知导入
何 时 面 积 最 大
如图 ,在一个直角三角形的内部作一个矩形 ABCD,其中 AB 和 AD 分别在两直角边上
讨论
由(1)得
D
A
B
C
40m
30m
x m
E
F
x m
(2)设矩形的面积为 y m ,当 x 取何值时,y 的值最大?最大值是多少?
矩形ABCD的面积
y= ×
= ×
= ;
AB
AD
x
(30 - )
- +30
y是x的二次函数
y=
- +30
=- +300
= 30 -
(0<x <40)
填一填
当 x =20m时,y 最大值=300m
新知探究
议一议
矩形改为如图 所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
D
A
B
C
40m
30m
x m
E
F
x m
设矩形的一边 AB = x m
G
H
M
过M作MG⊥EF,垂足为G,交AD于H
∴GH=xm
由勾股定理得:EF=50m
∵S△MEF
=EF
=ME
∴MG=24m
∵AD∥EF
∴△AMD∽△FME
∴ =
∴ =
∴ = 50 -
y=
- +50
y=x
(50 - )
=- +300
当 x =12m时,y 最大值=300m
(0<x <24)
第一步:审题理解问题;
第二步:分析问题中的 和常量, 自变量;
第三步:分析问题中的变量和常量之间的关系,建立函数的 ;
第四步:确定 的取值范围;
第五步:根据顶点坐标公式或配方法求出最 值或最 值(在自变量的取值范围内)。
议一议
新知探究
确定图形面积的最值
变量
设出
关系式
自变量
大
小
思考
你能总结出解决此类问题“最大面积”的基本思路吗
例题讲解
做一做
例1、某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15 m.当x等于多少时,窗户通过的光线最多(结果精确到0.01 m) 此时,窗户的面积是多少
x
x
y
2x
分析:
变量
半圆半径x
矩形的一边长2x,另一边长y
窗户面积S
自变量
相等关系
材料总长(图中所有的黑线的长度和)为15
7x+4y+πx=15
窗户的面积=半圆面积+矩形面积
找出y与x之间关系式
把y用x的代数式替换的S与x的函数关系式
例题讲解
做一做
例1、某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15 m.当x等于多少时,窗户通过的光线最多(结果精确到0.01 m) 此时,窗户的面积是多少
x
x
y
解:∵7x+4y+πx=15
2x
∴0<x<1.48.
设窗户的面积是S m2, 则
答:当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为4.02 m2.
方 法 规 律:
新知总结
(1)理清题目中的变量和常量.
(2)熟记常用几何图形的面积公式.
(3)选择合适的二次函数表达式解题.
何 时 面 积 最 大
例题讲解
做一做
例2、如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
x
x
60-2x
设菜园面积为S,垂直于墙的边长为x米,由题意得
解:
S=x(60-2x)
=-2x2+60x
=-2(x-15)+450
自变量x的取值范围是什么?
思考:
∵0<60-2x≤32,
∴14≤x<30.
墙长32m
∴最值在其顶点处,
即当x=15m时,S最大值=450m2.
∴抛物线开口向下,顶点坐标(15,450)
例题讲解
做一做
变式
x
x
60-2x
墙长18m
墙长32m
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
问题1 变式与例2有什么异同?
思考:
问题2 可否模仿例2设未知数、列函数关系式?
设菜园面积为S,垂直于墙的边长为x米,由题意得
S=x(60-2x)
=-2x2+60x
=-2(x-15)+450
问题3 自变量x的取值范围是什么?
∴抛物线开口向下,顶点坐标(15,450)
∵0<60-2x≤18,
∴21≤ x<30.
问题4 当x=15时,S取最大值,此结论是否正确?
不正确.
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
例题讲解
做一做
设菜园面积为S,垂直于墙的边长为x米,由题意得
S=x(60-2x)
=-2x2+60x
=-2(x-15) +450
∴抛物线开口向下,顶点坐标(15,450)
x
x
60-2x
解:
变式
∵0<60-2x≤18,
∴21≤ x<30.
利用函数的增减性求其最值
∵15<21,
∴顶点(15,450)不在自变量取值范围内
∵当x≥21时,S岁x的增大而减小
∴当x=21m时,S有最大值,
S最大值=378(m )
新知总结
何 时 面 积 最 大
当自变量的范围有限制时,二次函数 的最值可以根据以下步骤来确定:
1.配方,求二次函数的顶点坐标及对称轴.
2.画出函数图象,标明对称轴,并在横坐标上标明x的取值范围.
3.判断,判断x的取值范围与对称轴的位置关系.根据二次函数的性质,确定当x取何值时函数有最大或最小值.然后根据x的值,求出函数的最值.
实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量的取值范围
新知巩固
选一选
1、如图,正方形ABCD的边长为1,E、F、G、H盼别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为S,AE为x,则S关于x的函数图象大致是( )
B
小正方形EFGH的面积=正方形ABCD的面积-4倍Rt△AEH的面积
S=1-2x(1-x)
=2x -2x+1
=2(x-) +
(0<x <1)
分析:
新知巩固
选一选
2、如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( ).
A.60平方米
B.63平方米
C.64平方米
D.66平方米
A
B
C
D
分析:
矩形ABCD的面积S
=AB×BC
=x(16-x)
x
16-x
B
(2023·黑龙江大庆·统考中考真题)如图1,在平行四边形ABCD 中,∠ABC=120 ,已知点P 在边AB 上,以1m/s的速度从点A 向点B 运动,点Q 在边BC 上,以 的速度从点B 向点C 运动.若点P ,Q 同时出发,当点P 到达点 B时,点 Q恰好到达点 C处,此时两点都停止运动.图2是△BPQ 的面积y(m ) 与点 P的运动时间t(s) 之间的函数关系图象(点M 为图象的最高点),则平行四边形ABCD 的面积为( )
A.12m B. 24m C. 12m D. 24m
B
新知巩固
选一选
新知巩固
做一做
1.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为2cm/s,点Q的速度为1cm/s,点P移动到B点后停止,点Q也随之停止运动,设P、Q从点A、B同时出发,运动时间为t s,四边形APQC的面积是S
(1)试写出S与t之间的函数关系式,并确定自变量的取值范围;
A
B
C
P
Q
解:(1)∵在△ABC中,∠ABC=90°,
AB=8cm,BC=6cm
∴运动ts时,AP=2t,BP=8-2t,BQ=t
∴S=S△ABC-S△PBQ=×AB×CB-×PB×QB
=×8×6-×(8-2t)×t
=t2-4t+24(0≤t≤4)
新知巩固
选一选
(3)∵S=t2-4t+24
=(t-2)2+20,
∴当t=2时,S有最小值,S最小值=20
A
B
C
P
Q
(2)若S是21cm2时,确定t值;
S=t2-4t+24(0≤t≤4)
(2)由(1)得:
当S=21时,代入得
t2-4t+24=21,
解得t=1或t=3
(3)t为何值时,S有最大(或最小)值,求出这个最值.
课堂小结
实际问题
数学模型
转化
回归
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
课后拓展
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,求该纸盒侧面积的最大值
解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形ADOK≌筝形BEPF≌筝形AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结AO,
在Rt△AOD和Rt△AOK中,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设OD=x,则AO=2x,由勾股定理就可以求出AD=x
∴纸盒侧面积=3x(6﹣2x)=6x2+18x,
=﹣6(x-) +
∴当x=
纸盒侧面积最大为
如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A. m B.6m C.25m D. m
课后拓展
D
分析:
3.6 二次函数的应用
第三章 二次函数
第一课时
教学目标
1
2
3
1、.经历探究几何图形中的最值问题,学会用二次函数来解决几何图形中最值问题.体会二次函数的应用意义以及数学的转化思想.
2、通过自主探究,理解二次函数的应用.经过合作交流,了解二次函数解决几何图形最值问题的基本思路,提高学生的分析总结能力.
3、通过几何图形中的最值问题的探究活动,建立学生对二次函数应用的以及数形结合的思维,培养学生勇于探索的学习习惯.
知识回顾
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
二次函数的性质与解析式系数的关系
当x=-=,
y最小值= =-
知识回顾
二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值?
a>0
a<0
当x=-,函数值有最大值,y最大值=
当x=-,函数值有最大值,y最小值=
1、求下列函数的最大值或最小值:
①y=x2-4x+7 ②y=-5x2+8x-1
配方法
公式法
练一练
选择合适的方法
①y=x2-4x+7
=(x-2)2+3
当x=2时,y最小值=3
练一练
知识回顾
2.二次函数y=ax2+bx+c,b2=ac,且x=0时y=-4,则( )
A 、y最大=-4 B、y最小=-4 C、y最大=-3 D、y最小=3
把x=0,y=-4代入得:
c=-4
∵b2=ac>0
∴a<0
解析:
∴抛物线开口向下,函数有最大值
∴y最大值= = =-3
C
新知导入
何 时 面 积 最 大
如图 ,在一个直角三角形的内部作一个矩形 ABCD,其中 AB 和 AD 分别在两直角边上
D
A
B
C
40m
30m
(1)如果设矩形的一边 AB = x m,那么 AD边的长度如何表示?
讨论
x m
E
F
如图
∵AF∥DC
∴△AFE∽△DCE
∴ =
x m
∴ =
∵四边形ABCD矩形
∴AB=DC=Xm
∴ = 30 -
x的取值范围是什么?
0<x <40
新知导入
何 时 面 积 最 大
如图 ,在一个直角三角形的内部作一个矩形 ABCD,其中 AB 和 AD 分别在两直角边上
讨论
由(1)得
D
A
B
C
40m
30m
x m
E
F
x m
(2)设矩形的面积为 y m ,当 x 取何值时,y 的值最大?最大值是多少?
矩形ABCD的面积
y= ×
= ×
= ;
AB
AD
x
(30 - )
- +30
y是x的二次函数
y=
- +30
=- +300
= 30 -
(0<x <40)
填一填
当 x =20m时,y 最大值=300m
新知探究
议一议
矩形改为如图 所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
D
A
B
C
40m
30m
x m
E
F
x m
设矩形的一边 AB = x m
G
H
M
过M作MG⊥EF,垂足为G,交AD于H
∴GH=xm
由勾股定理得:EF=50m
∵S△MEF
=EF
=ME
∴MG=24m
∵AD∥EF
∴△AMD∽△FME
∴ =
∴ =
∴ = 50 -
y=
- +50
y=x
(50 - )
=- +300
当 x =12m时,y 最大值=300m
(0<x <24)
第一步:审题理解问题;
第二步:分析问题中的 和常量, 自变量;
第三步:分析问题中的变量和常量之间的关系,建立函数的 ;
第四步:确定 的取值范围;
第五步:根据顶点坐标公式或配方法求出最 值或最 值(在自变量的取值范围内)。
议一议
新知探究
确定图形面积的最值
变量
设出
关系式
自变量
大
小
思考
你能总结出解决此类问题“最大面积”的基本思路吗
例题讲解
做一做
例1、某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15 m.当x等于多少时,窗户通过的光线最多(结果精确到0.01 m) 此时,窗户的面积是多少
x
x
y
2x
分析:
变量
半圆半径x
矩形的一边长2x,另一边长y
窗户面积S
自变量
相等关系
材料总长(图中所有的黑线的长度和)为15
7x+4y+πx=15
窗户的面积=半圆面积+矩形面积
找出y与x之间关系式
把y用x的代数式替换的S与x的函数关系式
例题讲解
做一做
例1、某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15 m.当x等于多少时,窗户通过的光线最多(结果精确到0.01 m) 此时,窗户的面积是多少
x
x
y
解:∵7x+4y+πx=15
2x
∴0<x<1.48.
设窗户的面积是S m2, 则
答:当x约为1.07m时,窗户通过的光线最多.
此时,窗户的面积约为4.02 m2.
方 法 规 律:
新知总结
(1)理清题目中的变量和常量.
(2)熟记常用几何图形的面积公式.
(3)选择合适的二次函数表达式解题.
何 时 面 积 最 大
例题讲解
做一做
例2、如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
x
x
60-2x
设菜园面积为S,垂直于墙的边长为x米,由题意得
解:
S=x(60-2x)
=-2x2+60x
=-2(x-15)+450
自变量x的取值范围是什么?
思考:
∵0<60-2x≤32,
∴14≤x<30.
墙长32m
∴最值在其顶点处,
即当x=15m时,S最大值=450m2.
∴抛物线开口向下,顶点坐标(15,450)
例题讲解
做一做
变式
x
x
60-2x
墙长18m
墙长32m
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
问题1 变式与例2有什么异同?
思考:
问题2 可否模仿例2设未知数、列函数关系式?
设菜园面积为S,垂直于墙的边长为x米,由题意得
S=x(60-2x)
=-2x2+60x
=-2(x-15)+450
问题3 自变量x的取值范围是什么?
∴抛物线开口向下,顶点坐标(15,450)
∵0<60-2x≤18,
∴21≤ x<30.
问题4 当x=15时,S取最大值,此结论是否正确?
不正确.
如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
例题讲解
做一做
设菜园面积为S,垂直于墙的边长为x米,由题意得
S=x(60-2x)
=-2x2+60x
=-2(x-15) +450
∴抛物线开口向下,顶点坐标(15,450)
x
x
60-2x
解:
变式
∵0<60-2x≤18,
∴21≤ x<30.
利用函数的增减性求其最值
∵15<21,
∴顶点(15,450)不在自变量取值范围内
∵当x≥21时,S岁x的增大而减小
∴当x=21m时,S有最大值,
S最大值=378(m )
新知总结
何 时 面 积 最 大
当自变量的范围有限制时,二次函数 的最值可以根据以下步骤来确定:
1.配方,求二次函数的顶点坐标及对称轴.
2.画出函数图象,标明对称轴,并在横坐标上标明x的取值范围.
3.判断,判断x的取值范围与对称轴的位置关系.根据二次函数的性质,确定当x取何值时函数有最大或最小值.然后根据x的值,求出函数的最值.
实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量的取值范围
新知巩固
选一选
1、如图,正方形ABCD的边长为1,E、F、G、H盼别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为S,AE为x,则S关于x的函数图象大致是( )
B
小正方形EFGH的面积=正方形ABCD的面积-4倍Rt△AEH的面积
S=1-2x(1-x)
=2x -2x+1
=2(x-) +
(0<x <1)
分析:
新知巩固
选一选
2、如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( ).
A.60平方米
B.63平方米
C.64平方米
D.66平方米
A
B
C
D
分析:
矩形ABCD的面积S
=AB×BC
=x(16-x)
x
16-x
B
(2023·黑龙江大庆·统考中考真题)如图1,在平行四边形ABCD 中,∠ABC=120 ,已知点P 在边AB 上,以1m/s的速度从点A 向点B 运动,点Q 在边BC 上,以 的速度从点B 向点C 运动.若点P ,Q 同时出发,当点P 到达点 B时,点 Q恰好到达点 C处,此时两点都停止运动.图2是△BPQ 的面积y(m ) 与点 P的运动时间t(s) 之间的函数关系图象(点M 为图象的最高点),则平行四边形ABCD 的面积为( )
A.12m B. 24m C. 12m D. 24m
B
新知巩固
选一选
新知巩固
做一做
1.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为2cm/s,点Q的速度为1cm/s,点P移动到B点后停止,点Q也随之停止运动,设P、Q从点A、B同时出发,运动时间为t s,四边形APQC的面积是S
(1)试写出S与t之间的函数关系式,并确定自变量的取值范围;
A
B
C
P
Q
解:(1)∵在△ABC中,∠ABC=90°,
AB=8cm,BC=6cm
∴运动ts时,AP=2t,BP=8-2t,BQ=t
∴S=S△ABC-S△PBQ=×AB×CB-×PB×QB
=×8×6-×(8-2t)×t
=t2-4t+24(0≤t≤4)
新知巩固
选一选
(3)∵S=t2-4t+24
=(t-2)2+20,
∴当t=2时,S有最小值,S最小值=20
A
B
C
P
Q
(2)若S是21cm2时,确定t值;
S=t2-4t+24(0≤t≤4)
(2)由(1)得:
当S=21时,代入得
t2-4t+24=21,
解得t=1或t=3
(3)t为何值时,S有最大(或最小)值,求出这个最值.
课堂小结
实际问题
数学模型
转化
回归
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
课后拓展
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,求该纸盒侧面积的最大值
解:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形ADOK≌筝形BEPF≌筝形AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形ODEP、四边形PFGQ、四边形QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结AO,
在Rt△AOD和Rt△AOK中,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设OD=x,则AO=2x,由勾股定理就可以求出AD=x
∴纸盒侧面积=3x(6﹣2x)=6x2+18x,
=﹣6(x-) +
∴当x=
纸盒侧面积最大为
如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A. m B.6m C.25m D. m
课后拓展
D
分析:
