6.2.2反比例函数的性质 课件(共18张PPT)-九年级数学上册精品课堂(北师大版)
文档属性
| 名称 | 6.2.2反比例函数的性质 课件(共18张PPT)-九年级数学上册精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 494.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 20:26:14 | ||
图片预览



文档简介
(共18张PPT)
6.2.2 反比例函数的性质
第六章 反比例函数
北师大版九年级数学上册
学习&目标
1.理解并掌握反比例函数图象的性质;(重点)
2.能利用反比例函数的图象与性质解决问题.(难点)
情景&导入
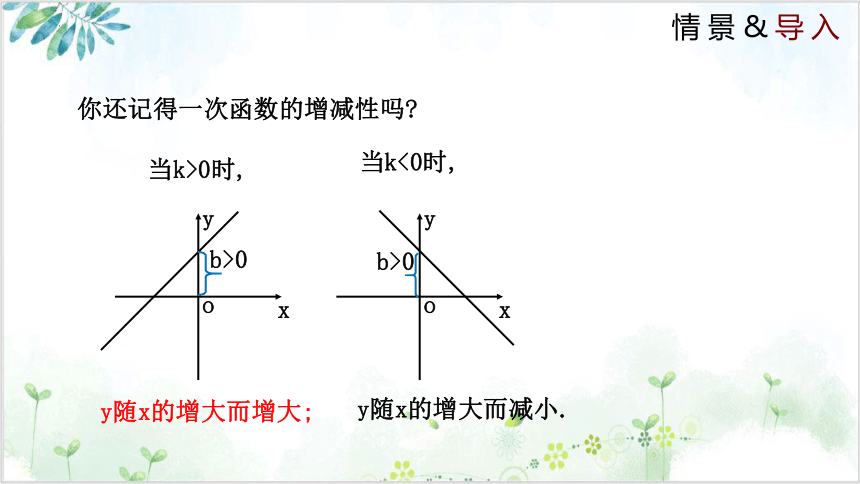
y随x的增大而增大;
你还记得一次函数的增减性吗
x
y
o
x
y
o
y随x的增大而减小.
b>0
b>0
当k>0时,
当k<0时,
探索&交流
反比例函数的性质
1—
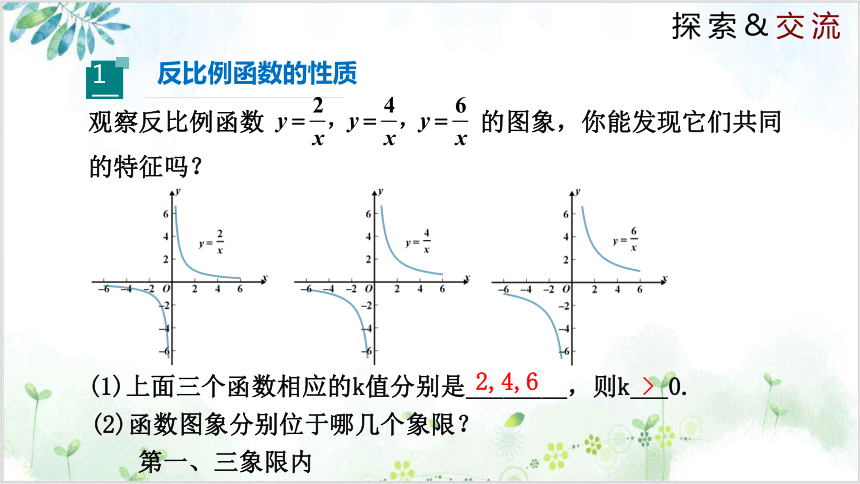
观察反比例函数 的图象,你能发现它们共同的特征吗?
(2)函数图象分别位于哪几个象限?
第一、三象限内
(1)上面三个函数相应的k值分别是________,则k___0.
2,4,6
>
探索&交流
x<0时,图象在第一象限;x>0 时,图象在第三象限.
(4)在每一象限内,曲线从左往右______,所以随着x值的增大,y的值怎样变化?
逐渐下降,减小.
(3)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?
探索&交流
议一议
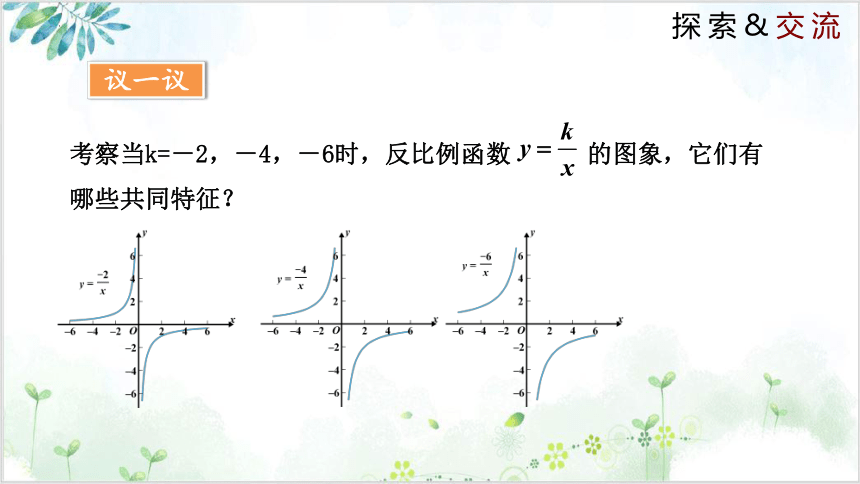
考察当k=-2,-4,-6时,反比例函数 的图象,它们有哪些共同特征?
探索&交流
归 纳
y
x
y
0
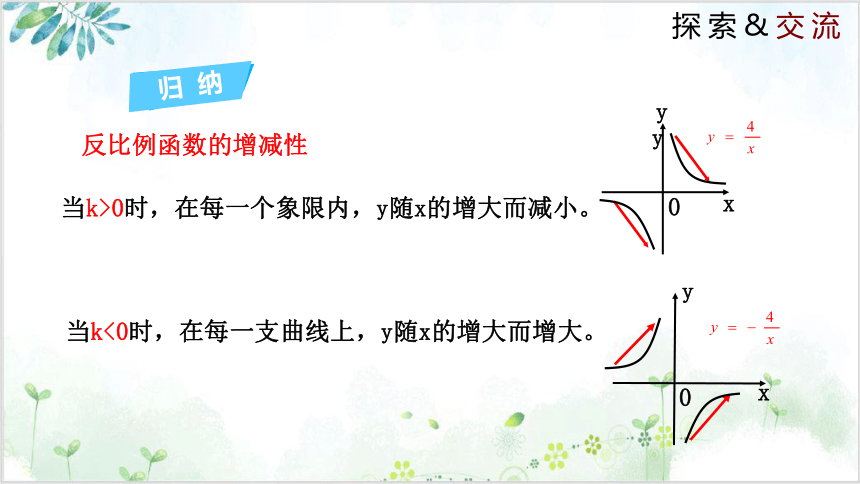
反比例函数的增减性
当k>0时,在每一个象限内,y随x的增大而减小。
当k<0时,在每一支曲线上,y随x的增大而增大。
x
y
0
探索&交流
归纳总结
(1)当k>0时,图象的两个分支分别在第一、三象限内,在每一象限内,y的值随x值的增大而减小;
(2)当k<0时,图象的两个分支分别在第二、四象限内,在每一象限内,y的值随x值的增大而增大.
一般地,反比例函数 的图象是双曲线,它具有以下性质:
k 的正负决定反比例函数所在的象限和增减性
探索&交流
想一想
Q
在一个反比例函数图象上任取两点P、Q,过点P分别做x轴、y轴的平行线,与坐标轴围成的矩形面积为S1;过点Q分别做x轴、y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2有什么关系?
P
S1
S2
探索&交流
Q
P
S1
S2
设P点坐标为(x1,y1),Q点坐标(x2,y2),
则S1=|x1| |y1|
=|k|
S2=|x2| |y2|
=|k|
S1=S2=|k|
探索&交流
三角形的面积:
如图6-2-3,过双曲线上任意一点E作EF垂直于y轴,垂足为F,连接EO,则S △EOF= ,即过双曲线上任意一点作一坐标轴的垂线,连接该点与原点,
所得三角形的面积为.
例题&解析
例题欣赏
例2.如图,过反比例函数 图象上的一点P,作PA⊥x轴于A.若△POA的面积为6,则k= .
y
x
O
P
A
﹣12
例题&解析
例题欣赏
例3.如图,一次函数y=ax+b的图象与反比例函数的图象交于A(-4,2),B(2,n)两点,且与x轴交于点C.(1)试确定上述反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)根据图象写出一次函数的值小于反比例
函数的值时x的取值范围.
例题&解析
解:(1)设反比例函数的表达式为y= (k≠0).
∵反比例函数的图象经过A(-4,2),
∴k=-8,∴反比例函数的表达式为y= =- .
∵B(2,n)在y=- 上,
∴n=- =-4,
∴点B的坐标是(2,-4).
把A(-4,2),B(2,-4)代入y=ax+b中,得
∴一次函数的表达为y=-x-2;
-4a+b=2,
2a+b=-4,
解得
a=-1,
b=-2,
练习&巩固
m<2
练习&巩固
2.已知两点P1(x1,y1),P2(x2,y2)在函数 的图象上,当x1>x2>0时,下列结论正确的是 ( )
A.0<y1<y2 B.0<y2<y1
C.y1<y2<0 D.y2<y1<0
A
练习&巩固
3.如图所示,反比例函数 (k≠0)的图象上有一点A, AB ∥x轴交y轴于点B,△ABO的面积是1,则反比例函数的表达式是( )
A. B. C. D.
y
x
O
A
B
C
小结&反思
反比例函数的性质
性质
反比例函数图象中比例系数k的几何意义
当k>0时,在每一象限内,y的值随x
的增大而减小.
当k<0时,在每一象限内,y的值随x
的增大而增大.
6.2.2 反比例函数的性质
第六章 反比例函数
北师大版九年级数学上册
学习&目标
1.理解并掌握反比例函数图象的性质;(重点)
2.能利用反比例函数的图象与性质解决问题.(难点)
情景&导入
y随x的增大而增大;
你还记得一次函数的增减性吗
x
y
o
x
y
o
y随x的增大而减小.
b>0
b>0
当k>0时,
当k<0时,
探索&交流
反比例函数的性质
1—
观察反比例函数 的图象,你能发现它们共同的特征吗?
(2)函数图象分别位于哪几个象限?
第一、三象限内
(1)上面三个函数相应的k值分别是________,则k___0.
2,4,6
>
探索&交流
x<0时,图象在第一象限;x>0 时,图象在第三象限.
(4)在每一象限内,曲线从左往右______,所以随着x值的增大,y的值怎样变化?
逐渐下降,减小.
(3)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?
探索&交流
议一议
考察当k=-2,-4,-6时,反比例函数 的图象,它们有哪些共同特征?
探索&交流
归 纳
y
x
y
0
反比例函数的增减性
当k>0时,在每一个象限内,y随x的增大而减小。
当k<0时,在每一支曲线上,y随x的增大而增大。
x
y
0
探索&交流
归纳总结
(1)当k>0时,图象的两个分支分别在第一、三象限内,在每一象限内,y的值随x值的增大而减小;
(2)当k<0时,图象的两个分支分别在第二、四象限内,在每一象限内,y的值随x值的增大而增大.
一般地,反比例函数 的图象是双曲线,它具有以下性质:
k 的正负决定反比例函数所在的象限和增减性
探索&交流
想一想
Q
在一个反比例函数图象上任取两点P、Q,过点P分别做x轴、y轴的平行线,与坐标轴围成的矩形面积为S1;过点Q分别做x轴、y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2有什么关系?
P
S1
S2
探索&交流
Q
P
S1
S2
设P点坐标为(x1,y1),Q点坐标(x2,y2),
则S1=|x1| |y1|
=|k|
S2=|x2| |y2|
=|k|
S1=S2=|k|
探索&交流
三角形的面积:
如图6-2-3,过双曲线上任意一点E作EF垂直于y轴,垂足为F,连接EO,则S △EOF= ,即过双曲线上任意一点作一坐标轴的垂线,连接该点与原点,
所得三角形的面积为.
例题&解析
例题欣赏
例2.如图,过反比例函数 图象上的一点P,作PA⊥x轴于A.若△POA的面积为6,则k= .
y
x
O
P
A
﹣12
例题&解析
例题欣赏
例3.如图,一次函数y=ax+b的图象与反比例函数的图象交于A(-4,2),B(2,n)两点,且与x轴交于点C.(1)试确定上述反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)根据图象写出一次函数的值小于反比例
函数的值时x的取值范围.
例题&解析
解:(1)设反比例函数的表达式为y= (k≠0).
∵反比例函数的图象经过A(-4,2),
∴k=-8,∴反比例函数的表达式为y= =- .
∵B(2,n)在y=- 上,
∴n=- =-4,
∴点B的坐标是(2,-4).
把A(-4,2),B(2,-4)代入y=ax+b中,得
∴一次函数的表达为y=-x-2;
-4a+b=2,
2a+b=-4,
解得
a=-1,
b=-2,
练习&巩固
m<2
练习&巩固
2.已知两点P1(x1,y1),P2(x2,y2)在函数 的图象上,当x1>x2>0时,下列结论正确的是 ( )
A.0<y1<y2 B.0<y2<y1
C.y1<y2<0 D.y2<y1<0
A
练习&巩固
3.如图所示,反比例函数 (k≠0)的图象上有一点A, AB ∥x轴交y轴于点B,△ABO的面积是1,则反比例函数的表达式是( )
A. B. C. D.
y
x
O
A
B
C
小结&反思
反比例函数的性质
性质
反比例函数图象中比例系数k的几何意义
当k>0时,在每一象限内,y的值随x
的增大而减小.
当k<0时,在每一象限内,y的值随x
的增大而增大.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
