4.3.3用一元一次方程解决问题——比例问题、规律问题和工程问题 课件(共24张PPT)-七年级数学上册精品课堂(苏科版2024)
文档属性
| 名称 | 4.3.3用一元一次方程解决问题——比例问题、规律问题和工程问题 课件(共24张PPT)-七年级数学上册精品课堂(苏科版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 41.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 16:08:42 | ||
图片预览







文档简介
(共24张PPT)
4.3.3 用一元一次方程解决问题——比例问题、规律问题和工程问题
第4章 一元一次方程
教学目标
01
能用一元一次方程解决比例问题、规律问题和鸡兔同笼问题
02
掌握与工程问题有关的基本公式,进一步用一元一次方程解决工程问题,并熟练地将“单位1”的思想应用其中
问 题 目 录
销售问题
比例问题
行程问题
……
已知三角形三个角的度数之比为2:3:5,判断这个三角形的形状。
【分析】隐藏的等量关系:
第一个角+第二个角+第三个角=180°
解:设三角形三个角的大小分别为2x,3x,5x,
02
知识精讲
根据题意得:2x+3x+5x=180°,
解得:x=18°,∴2x=36°,3x=54°,5x=90°,
∴三角形三个角的大小分别为36°,54°,90°,
答:这个三角形是直角三角形。
例、将一个圆分割成四个扇形,使四个扇形的面积之比为1:2:3:4,则四个扇形圆心角度数最大的是________。
【分析】隐藏的等量关系:四个扇形的圆心角度数之和=360°
03
典例精析
解:∵四个扇形的面积之比为1:2:3:4,
∴它们的圆心角的度数之比为1:2:3:4,
设角的度数分别为x,2x,3x,4x,
根据题意得:x+2x+3x+4x=360°,解得:x=36°,
∴2x=72°,3x=108°,4x=144°,
答:四个扇形圆心角度数最大的是144°。
144°
问 题 目 录
销售问题
比例问题
行程问题
规律问题
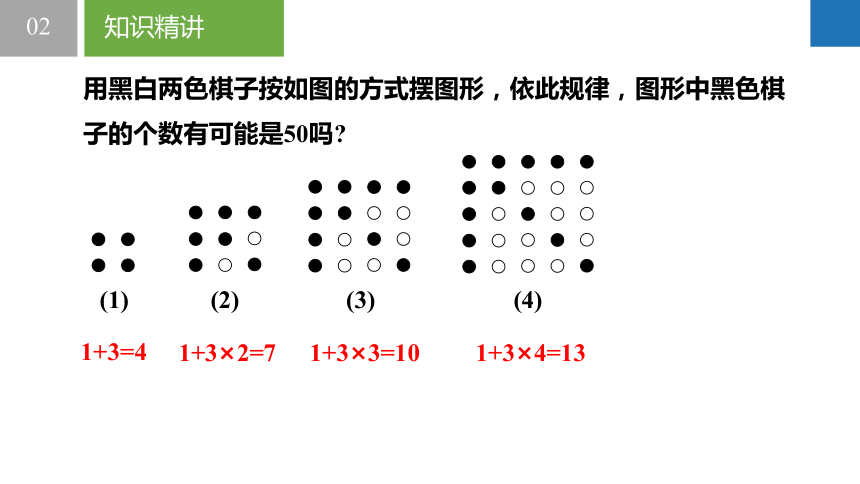
用黑白两色棋子按如图的方式摆图形,依此规律,图形中黑色棋子的个数有可能是50吗
02
知识精讲
(1) (2) (3) (4)
1+3=4
1+3×2=7
1+3×3=10
1+3×4=13
02
知识精讲
1+3=4
1+3×2=7
1+3×3=10
1+3×4=13
解:设第m个图形中有黑色棋子50个,
解得:m=,
m=不是整数,不符合题意,
答:图形中黑色棋子的个数不可能是50。
根据题意得:3m+1=50,
例、用火柴棒按如图的方式搭图形。
小静同学说她按这种方式搭出来的一个图形用了2001根火柴棒,你认为可能吗?如果可能,那么是第几个图形?如果不可能,请说明理由。
03
典例精析
图形 1 2 3 …
火柴棒根数 …
1+4=5 1+4×2=9 1+4×3=13
03
典例精析
解:设第n个图形中有2001根火柴棒,
图形 1 2 3 …
火柴棒根数 1+4=5 1+4×2=9 1+4×3=13 …
根据题意得:4n+1=2001,
解得:n=500,符合题意,
答:可能,第500个图形中有2001根火柴棒。
问 题 目 录
销售问题
比例问题
行程问题
规律问题
鸡兔同笼
请解决章头活动中的鸡兔同笼问题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何
【分析】设鸡有x只,可以列出表格分析数量关系:
02
知识精讲
项目 只数 足数
鸡 x
兔
合计 35 94
2x
35-x 4(35-x)
解:设鸡有x只,
根据题意得:2x+4(35-x)=94,
解得:x=23,
35-x=12,
答:鸡有23只,兔有12只。
02
知识精讲
例、七(2)班的王老师和张老师带领40名学生去公园野营,大帐篷限住5人,小帐篷限住3人,一共租了10顶帐篷,正好全部住满。大帐篷和小帐篷各租了多少顶?
03
典例精析
【分析】设大帐篷有x顶,可以列出表格分析数量关系:
项目 帐篷数 总人数
大帐篷 x
小帐篷
合计 10
5x
10-x 3(10-x)
40+2=42
03
典例精析
解:设大帐篷租了x顶,则小帐篷租了(10-x)顶,
根据题意得:5x+3(10-x)=40+2,
解得:x=6,
∴10-x=10-6=4,
答:大帐篷租了6顶,小帐篷租了4顶。
问 题 目 录
销售问题
比例问题
行程问题
规律问题
鸡兔同笼
工程问题
01
情境引入
“愚公移山”的故事家喻户晓,在技术受限的战国时期,祖祖辈辈移山的行为令人钦佩
现今,工程队配上挖掘机就可以轻轻松松移山了
01
情境引入
Q1:某工程队计划将该市的600套老旧房屋进行翻新改造,若每天翻新改造10套老旧房屋,则该工程队需要多少天才能完工?
Q2:(1)工程问题中的基本量是什么?
(2)这些基本量之间的关系是什么?
工作总量=工作效率×工作时间
工作总量、工作效率、工作时间
工程队需要的天数==60天
02
02
知识精讲
一项工程,甲单独做30天完成,乙单独做15天完成。若甲、乙合作,多少天可以完成这项工程?
未知工作效率和工作总量该如何列式呢?
若是知道工作总量,甲、乙的工作效率就可以分别表示出来了
不妨设工作总量为单位1
【分析】等量关系:甲完成的工作量+乙完成的工作量=工程总量
02
02
知识精讲
复习“单位1”的概念:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
02
02
知识精讲
解:设这项工程为1,且甲、乙合作,x天可以完成这项工程,
解得:x=10,
答:甲、乙合作,10天可以完成这项工程。
【分析】
若这项工程为“1”,则甲的工作效率为,乙的工作效率为,
根据题意得:+=1,
例1、某工厂计划26小时生产一批零件,后因每小时多生产5件,用24小时,不但完成了任务,而且还比原计划多生产了60件,问原计划生产多少零件?
【分析】等量关系:实际工作效率-原计划工作效率=5件/小时
03
典例精析
解:设工作总量为1,且原计划生产x个零件,
则实际生产(x+60)个零件,
根据题意得:-=5,
解得:x=780,答:原计划生产780个零件。
例2、一项工程,甲单独做要10天完成,乙单独做要15天完成,两人合做4天后,剩下的部分由乙单独做,还需要几天完成?
【分析】等量关系:合做的工作量+乙单独做的工作量=工作总量
03
典例精析
解:设这项工程为1,且剩余的部分由乙单独做,还需要x天完成,
根据题意得:(+)×4+x=1,
解得:x=5,
答:剩余的部分由乙单独做,还需要5天完成。
课后总结
单位1:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
4.3.3 用一元一次方程解决问题——比例问题、规律问题和工程问题
第4章 一元一次方程
教学目标
01
能用一元一次方程解决比例问题、规律问题和鸡兔同笼问题
02
掌握与工程问题有关的基本公式,进一步用一元一次方程解决工程问题,并熟练地将“单位1”的思想应用其中
问 题 目 录
销售问题
比例问题
行程问题
……
已知三角形三个角的度数之比为2:3:5,判断这个三角形的形状。
【分析】隐藏的等量关系:
第一个角+第二个角+第三个角=180°
解:设三角形三个角的大小分别为2x,3x,5x,
02
知识精讲
根据题意得:2x+3x+5x=180°,
解得:x=18°,∴2x=36°,3x=54°,5x=90°,
∴三角形三个角的大小分别为36°,54°,90°,
答:这个三角形是直角三角形。
例、将一个圆分割成四个扇形,使四个扇形的面积之比为1:2:3:4,则四个扇形圆心角度数最大的是________。
【分析】隐藏的等量关系:四个扇形的圆心角度数之和=360°
03
典例精析
解:∵四个扇形的面积之比为1:2:3:4,
∴它们的圆心角的度数之比为1:2:3:4,
设角的度数分别为x,2x,3x,4x,
根据题意得:x+2x+3x+4x=360°,解得:x=36°,
∴2x=72°,3x=108°,4x=144°,
答:四个扇形圆心角度数最大的是144°。
144°
问 题 目 录
销售问题
比例问题
行程问题
规律问题
用黑白两色棋子按如图的方式摆图形,依此规律,图形中黑色棋子的个数有可能是50吗
02
知识精讲
(1) (2) (3) (4)
1+3=4
1+3×2=7
1+3×3=10
1+3×4=13
02
知识精讲
1+3=4
1+3×2=7
1+3×3=10
1+3×4=13
解:设第m个图形中有黑色棋子50个,
解得:m=,
m=不是整数,不符合题意,
答:图形中黑色棋子的个数不可能是50。
根据题意得:3m+1=50,
例、用火柴棒按如图的方式搭图形。
小静同学说她按这种方式搭出来的一个图形用了2001根火柴棒,你认为可能吗?如果可能,那么是第几个图形?如果不可能,请说明理由。
03
典例精析
图形 1 2 3 …
火柴棒根数 …
1+4=5 1+4×2=9 1+4×3=13
03
典例精析
解:设第n个图形中有2001根火柴棒,
图形 1 2 3 …
火柴棒根数 1+4=5 1+4×2=9 1+4×3=13 …
根据题意得:4n+1=2001,
解得:n=500,符合题意,
答:可能,第500个图形中有2001根火柴棒。
问 题 目 录
销售问题
比例问题
行程问题
规律问题
鸡兔同笼
请解决章头活动中的鸡兔同笼问题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何
【分析】设鸡有x只,可以列出表格分析数量关系:
02
知识精讲
项目 只数 足数
鸡 x
兔
合计 35 94
2x
35-x 4(35-x)
解:设鸡有x只,
根据题意得:2x+4(35-x)=94,
解得:x=23,
35-x=12,
答:鸡有23只,兔有12只。
02
知识精讲
例、七(2)班的王老师和张老师带领40名学生去公园野营,大帐篷限住5人,小帐篷限住3人,一共租了10顶帐篷,正好全部住满。大帐篷和小帐篷各租了多少顶?
03
典例精析
【分析】设大帐篷有x顶,可以列出表格分析数量关系:
项目 帐篷数 总人数
大帐篷 x
小帐篷
合计 10
5x
10-x 3(10-x)
40+2=42
03
典例精析
解:设大帐篷租了x顶,则小帐篷租了(10-x)顶,
根据题意得:5x+3(10-x)=40+2,
解得:x=6,
∴10-x=10-6=4,
答:大帐篷租了6顶,小帐篷租了4顶。
问 题 目 录
销售问题
比例问题
行程问题
规律问题
鸡兔同笼
工程问题
01
情境引入
“愚公移山”的故事家喻户晓,在技术受限的战国时期,祖祖辈辈移山的行为令人钦佩
现今,工程队配上挖掘机就可以轻轻松松移山了
01
情境引入
Q1:某工程队计划将该市的600套老旧房屋进行翻新改造,若每天翻新改造10套老旧房屋,则该工程队需要多少天才能完工?
Q2:(1)工程问题中的基本量是什么?
(2)这些基本量之间的关系是什么?
工作总量=工作效率×工作时间
工作总量、工作效率、工作时间
工程队需要的天数==60天
02
02
知识精讲
一项工程,甲单独做30天完成,乙单独做15天完成。若甲、乙合作,多少天可以完成这项工程?
未知工作效率和工作总量该如何列式呢?
若是知道工作总量,甲、乙的工作效率就可以分别表示出来了
不妨设工作总量为单位1
【分析】等量关系:甲完成的工作量+乙完成的工作量=工程总量
02
02
知识精讲
复习“单位1”的概念:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
02
02
知识精讲
解:设这项工程为1,且甲、乙合作,x天可以完成这项工程,
解得:x=10,
答:甲、乙合作,10天可以完成这项工程。
【分析】
若这项工程为“1”,则甲的工作效率为,乙的工作效率为,
根据题意得:+=1,
例1、某工厂计划26小时生产一批零件,后因每小时多生产5件,用24小时,不但完成了任务,而且还比原计划多生产了60件,问原计划生产多少零件?
【分析】等量关系:实际工作效率-原计划工作效率=5件/小时
03
典例精析
解:设工作总量为1,且原计划生产x个零件,
则实际生产(x+60)个零件,
根据题意得:-=5,
解得:x=780,答:原计划生产780个零件。
例2、一项工程,甲单独做要10天完成,乙单独做要15天完成,两人合做4天后,剩下的部分由乙单独做,还需要几天完成?
【分析】等量关系:合做的工作量+乙单独做的工作量=工作总量
03
典例精析
解:设这项工程为1,且剩余的部分由乙单独做,还需要x天完成,
根据题意得:(+)×4+x=1,
解得:x=5,
答:剩余的部分由乙单独做,还需要5天完成。
课后总结
单位1:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
同课章节目录
