14.1.1同底数幂的乘法 课件(共18张PPT)-八年级数学上册精品课堂(人教版)
文档属性
| 名称 | 14.1.1同底数幂的乘法 课件(共18张PPT)-八年级数学上册精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
14.1.1同底数幂的乘法
主讲:
人教版数学八年级上册
第十四章 整式的乘法
与因式分解
1.理解并掌握同底数幂的乘法法则.
2.能够运用同底数幂的乘法法则进行相关计算.
3.通过对同底数幂的乘法运算法则的推导与总结,提升自身的推理能力.
学习目标
我们享受的日光实际上是八分钟之前的.已知光在真空中的速度大约是3×108 m/s,一束太阳光照射到地球大约需要8分20秒.请你以此为基础计算太阳与地球之间的距离.
太阳光照射到地球的时间
t=8分20秒=500秒=5×102 s
光在真空中的速度v=3×108 m/s,
因此太阳与地球之间的距离
s=vt=3×108×5×102 m
应该如何计算呢?
情境引入
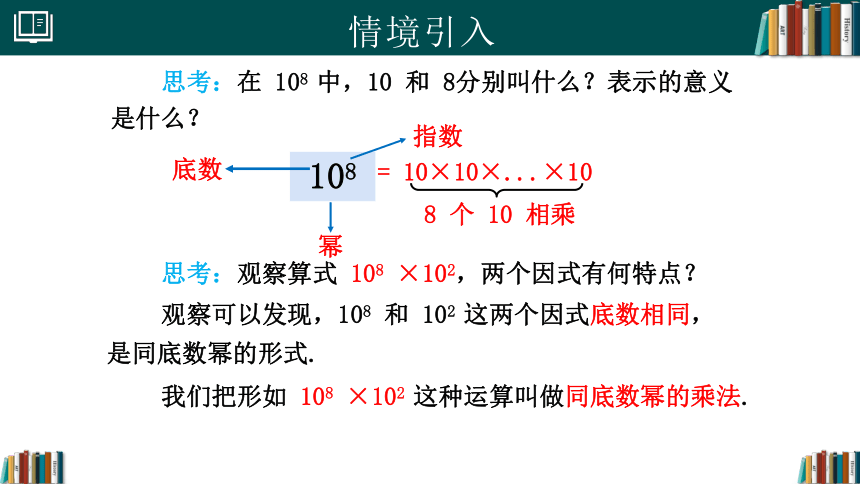
思考:在 108 中,10 和 8分别叫什么?表示的意义是什么?
= 10×10×...×10
8 个 10 相乘
108
底数
幂
指数
思考:观察算式 108 ×102,两个因式有何特点?
观察可以发现,108 和 102 这两个因式底数相同,是同底数幂的形式.
我们把形如 108 ×102 这种运算叫做同底数幂的乘法.
情境引入
在2010年全球超级计算机排行榜中,中国首台千万亿次超级计算机系统“天河一号”雄居第一,其实测运算速度可以达到每秒2570万亿次.
问题1 一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103s可进行多少次运算?
解:1015×103
=(10×10×…×10)×(10×10×10)
=10×10×…×10
=1018
15个10
3个10
18个10
新知探究
根据乘方的意义填空,观察计算结果,你能发现什么规律?
(1)25×22=2( )
(2)a3·a2=a( )
(3)5m×5n=5( ) (m,n是正整数)
7
5
m+n
思考:观察上面各题左右两边,底数、指数有什么关系?
相乘结果的底数与原来底数相同,指数是原来两个幂的指数的和.
新知探究
am an等于什么?(a是任意底数,m、n都是正整数)
=(a a … a)×(a a … a)
=a a … a
=am+n
am an
m个a
n个a
m+n个a
你能用一句语言来叙述这一规律吗?
新知探究
同底数幂乘法法则:
同底数幂相乘,底数不变,指数相加.
am an=am+n(m、n都是正整数)
条件:
结果:
①底数不变
①乘法
②同底数幂
②指数相加
新知探究
例1 计算:
(1) x2·x5; (2) a·a6;
(3)(-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解:(1)x2·x5 =x2+5 =x7.
(2)a·a6 =a1+6 =a7.
(3)(-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8=256.
(4)xm·x3m+1=xm+3m+1=x4m+1.
典例精析
1.下列运算中,正确的是( )
A.a3·a3=2a3 B.a3·a3=a6 C.a3·a3=a9 D.a3+a3=a6
2.化简(-x)3·(-x)4,结果正确的是( )
A.-x7 B.x7 C.x12 D.-x12
3.若am=3,an=5,则am+n等于( )
A.243 B.125 C.8 D.15
B
A
D
随堂检测
4.计算:
(1)b5·b ; (2) 10×102×103;
(3)–a2·a6; (4) y2n·yn+1.
解:(1)b5·b =x5+1 =b6.
(2)10×102×103=101+2+3 =106.
(3)-a2·a6=-a2+6=-a8.
(4)y2n·yn+1=y2n+n+1=y3n+1
随堂检测
5.我国自行设计制造的“神舟六号”飞船进入圆形轨道后的飞行速度为7.9×103米/秒,它绕地球一周需5.4×103秒,问该圆形轨道的一周有多少米?(结果用科学记数法表示)
解:
=
(米).
答:该圆形轨道的一周有米.
随堂检测
1.(1)已知an-3·a2n+1=a10恒成立,求n的值;
(2)已知xa=2,xb=3,求xa+b的值.
解:(1)n-3+2n+1=10,
n=4;
(2)xa+b=xa·xb=2×3=6.
能力提升
2.(1)已知 xa = 8,xb = 9,求 xa+b 的值;
(2)已知 an-3 · a2n+1 = a10,求 n 的值;
(3)3×27×9 = 32x-4,求 x 的值.
解:(1)xa+b = xa · xb = 8×9 = 72.
(2)n - 3 + 2n + 1 = 10,
∴ n = 4.
(3)3×27×9 = 3×33×32 = 32x-4,
∴ 2x - 4 = 6.
∴ x = 5.
能力提升
同底数幂
的乘法
法则:同底数幂相乘,底数
不变,指数相加.
am×an=am+n (m,n为正整数)
课堂小结
1.若m·23=26,则m等于( )
A.2 B.4 C.6 D.8
2.若a2n-1·an+2=a7,则n的值是( )
A.2 B.3 C.4 D.5
D
A
课后作业
3.计算:
(1)52×57; (2)7×73×72;
(3)-x2 x3; (4)(-c)3 (-c)m .
解:(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3)-x2 x3=-x2+3=-x5.
(4)(-c)3 (-c)m =(-c)3+m.
课后作业
主讲:
人教版八年级数学上册
感谢聆听
14.1.1同底数幂的乘法
主讲:
人教版数学八年级上册
第十四章 整式的乘法
与因式分解
1.理解并掌握同底数幂的乘法法则.
2.能够运用同底数幂的乘法法则进行相关计算.
3.通过对同底数幂的乘法运算法则的推导与总结,提升自身的推理能力.
学习目标
我们享受的日光实际上是八分钟之前的.已知光在真空中的速度大约是3×108 m/s,一束太阳光照射到地球大约需要8分20秒.请你以此为基础计算太阳与地球之间的距离.
太阳光照射到地球的时间
t=8分20秒=500秒=5×102 s
光在真空中的速度v=3×108 m/s,
因此太阳与地球之间的距离
s=vt=3×108×5×102 m
应该如何计算呢?
情境引入
思考:在 108 中,10 和 8分别叫什么?表示的意义是什么?
= 10×10×...×10
8 个 10 相乘
108
底数
幂
指数
思考:观察算式 108 ×102,两个因式有何特点?
观察可以发现,108 和 102 这两个因式底数相同,是同底数幂的形式.
我们把形如 108 ×102 这种运算叫做同底数幂的乘法.
情境引入
在2010年全球超级计算机排行榜中,中国首台千万亿次超级计算机系统“天河一号”雄居第一,其实测运算速度可以达到每秒2570万亿次.
问题1 一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103s可进行多少次运算?
解:1015×103
=(10×10×…×10)×(10×10×10)
=10×10×…×10
=1018
15个10
3个10
18个10
新知探究
根据乘方的意义填空,观察计算结果,你能发现什么规律?
(1)25×22=2( )
(2)a3·a2=a( )
(3)5m×5n=5( ) (m,n是正整数)
7
5
m+n
思考:观察上面各题左右两边,底数、指数有什么关系?
相乘结果的底数与原来底数相同,指数是原来两个幂的指数的和.
新知探究
am an等于什么?(a是任意底数,m、n都是正整数)
=(a a … a)×(a a … a)
=a a … a
=am+n
am an
m个a
n个a
m+n个a
你能用一句语言来叙述这一规律吗?
新知探究
同底数幂乘法法则:
同底数幂相乘,底数不变,指数相加.
am an=am+n(m、n都是正整数)
条件:
结果:
①底数不变
①乘法
②同底数幂
②指数相加
新知探究
例1 计算:
(1) x2·x5; (2) a·a6;
(3)(-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解:(1)x2·x5 =x2+5 =x7.
(2)a·a6 =a1+6 =a7.
(3)(-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8=256.
(4)xm·x3m+1=xm+3m+1=x4m+1.
典例精析
1.下列运算中,正确的是( )
A.a3·a3=2a3 B.a3·a3=a6 C.a3·a3=a9 D.a3+a3=a6
2.化简(-x)3·(-x)4,结果正确的是( )
A.-x7 B.x7 C.x12 D.-x12
3.若am=3,an=5,则am+n等于( )
A.243 B.125 C.8 D.15
B
A
D
随堂检测
4.计算:
(1)b5·b ; (2) 10×102×103;
(3)–a2·a6; (4) y2n·yn+1.
解:(1)b5·b =x5+1 =b6.
(2)10×102×103=101+2+3 =106.
(3)-a2·a6=-a2+6=-a8.
(4)y2n·yn+1=y2n+n+1=y3n+1
随堂检测
5.我国自行设计制造的“神舟六号”飞船进入圆形轨道后的飞行速度为7.9×103米/秒,它绕地球一周需5.4×103秒,问该圆形轨道的一周有多少米?(结果用科学记数法表示)
解:
=
(米).
答:该圆形轨道的一周有米.
随堂检测
1.(1)已知an-3·a2n+1=a10恒成立,求n的值;
(2)已知xa=2,xb=3,求xa+b的值.
解:(1)n-3+2n+1=10,
n=4;
(2)xa+b=xa·xb=2×3=6.
能力提升
2.(1)已知 xa = 8,xb = 9,求 xa+b 的值;
(2)已知 an-3 · a2n+1 = a10,求 n 的值;
(3)3×27×9 = 32x-4,求 x 的值.
解:(1)xa+b = xa · xb = 8×9 = 72.
(2)n - 3 + 2n + 1 = 10,
∴ n = 4.
(3)3×27×9 = 3×33×32 = 32x-4,
∴ 2x - 4 = 6.
∴ x = 5.
能力提升
同底数幂
的乘法
法则:同底数幂相乘,底数
不变,指数相加.
am×an=am+n (m,n为正整数)
课堂小结
1.若m·23=26,则m等于( )
A.2 B.4 C.6 D.8
2.若a2n-1·an+2=a7,则n的值是( )
A.2 B.3 C.4 D.5
D
A
课后作业
3.计算:
(1)52×57; (2)7×73×72;
(3)-x2 x3; (4)(-c)3 (-c)m .
解:(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3)-x2 x3=-x2+3=-x5.
(4)(-c)3 (-c)m =(-c)3+m.
课后作业
主讲:
人教版八年级数学上册
感谢聆听
