14.1.4整式的乘法(第3课时) 课件(共21张PPT)-八年级数学上册精品课堂(人教版)
文档属性
| 名称 | 14.1.4整式的乘法(第3课时) 课件(共21张PPT)-八年级数学上册精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 821.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
14.1.4 整式的乘法(第3课时)
主讲:
人教版数学八年级上册
第十四章 整式的乘法
与因式分解
1.探索并了解多项式与多项式相乘的法则,并运用它们进行运算.
2.让学生主动参与到探索过程中去,逐步形成独立思考、主动探索的习惯,培养思维的批判性、严密性和初步解决问题的能力.
学习目标
1.如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项,
2.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
复习引入
计算:1.单项式乘以单项式
2.单项式乘以多项式
(-3x)·(x2+4x);
解:原式=(-3x)·(x2)+(-3x)·4x
=-3x3-12x2;
(-4ab)·3a2bc;
解:原式=(-4×3)·(a·a2)·(b·b)·c
=-12a3b2c;
复习引入
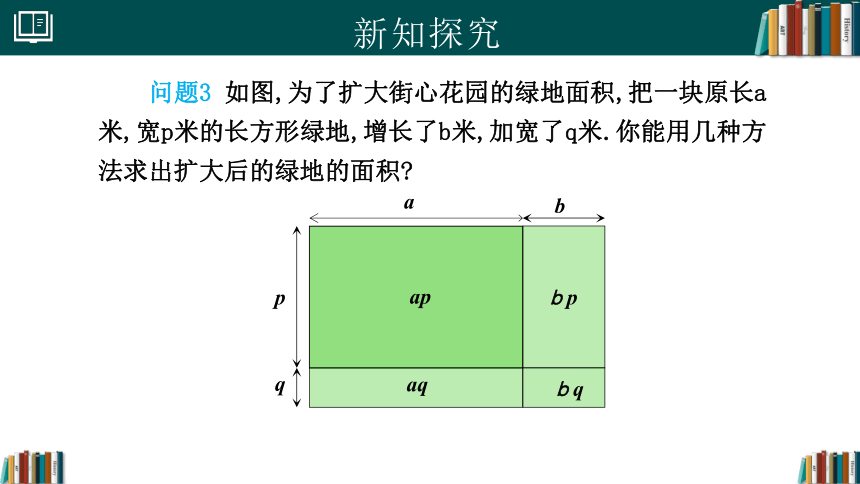
问题3 如图,为了扩大街心花园的绿地面积,把一块原长a米,宽p米的长方形绿地,增长了b米,加宽了q米.你能用几种方法求出扩大后的绿地的面积
p
q
a
b
ap
bq
bp
aq
新知探究
p
q
a
b
ap
bq
bp
aq
解法一:扩大后的绿地面积可以看成长为(a+b)m,宽为(p+q)m的长方形,所以这块绿地的面积为
(a+b)(p+q) ①
解法二:扩大后的绿地面积还可以看成由四个小长方形组成,所以这块绿地的面积为
ap+aq+bp+bq ②
新知探究
由于①和②表示同一个量,所以:
(a+b)(p+q)=ap+aq+bp+bq
多项式
多项式
思考:观察式子(a+b)(p+q)=ap+aq+bp+bq 的特征,你能说出多项式与多项式相乘的法则吗?
把p+q看做一个整体,运用单项式与多项式相乘的法则,得
(a+b)(p+q)=a(p+q)+b(p+q).
新知探究
再利用单项式与多项式相乘的法则,得
a(p+q)+b(p+q)=ap+aq+bp+bq.
总体上看,(a+b)(p+q)的结果可以看作由a+b的每一项乘p+q的每一项,再把所得的积相加而得到的,
即
(a+b)(p+q)=ap+aq+bp+bq
新知探究
(a+b)( p+q)=ap+aq+bp+bq
(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
推广:
注意:多项式与多项式相乘时,要按照一定的顺序进行,做到不重不漏.
新知探究
多项式与多项式相乘的步骤:
(1) 先用一个多项式的每一项分别乘以另一个多项式的每一项;
(2) 把各乘积相加;
(3) 有同类项的要合并同类项;
(4) 通常把结果整理成按某一字母的降幂排列.
总结归纳
例6 计算:
(1)(3x+1)(x+2); (2)(x-8y)(x-y);
(3) (x+y)(x2-xy+y2).
解:(1)原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(2) 原式=x·x+x·(-y)+(-8y)·x+(-8y)·(-y)
=x·x-xy-8xy+8y2
=x2-9xy+8y2;
结果中有同类项的要合并同类项.
计算时要注意符号问题.
典例精析
例6 计算:
(3) (x+y)(x2-xy+y2).
(3)原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
=x3+y3.
计算时不能漏乘.
需要注意的几个问题:(1)漏乘;
(2)符号问题;
(3)最后结果应化成最简形式.
典例精析
1.下列多项式相乘结果为a2-3a-18的是( )
A.(a-2)(a+9) B.(a+2)(a-9)
C.(a+3)(a-6) D.(a-3)(a+6)
2.下列各式中错误的是( )
A.(2a+3)(2a-3)=4a2-9
B.(3a+4b)2=9a2+24ab+4b2
C.(x+2)(x-10)=x2-8x-20
D.(x+y)(x2-xy+y2)=x3+y3
C
B
随堂检测
3.计算:
(1)(2x+1)(x+3) (2)(m+2n)(3n-m) (3)(a-1)2
(4)(a+3b)(a-3b) (5)(2x2-1)(x-4) (6)(x2+2x+3)(2x-5)
解:(1)原式=2x2+6x+x+3=2x2+7x+3
(2)原式=3mn-m2+6n2-2mn=mn-m2+6n2
(3)原式=(a-1)(a-1)=a2-a-a+1=a2-2a+1
(4)原式=a2-3ab+3ab-9b2=a2-9b2
(5)原式=2x2-8x2-x+4
(6)原式=2x3-5x2+4x2-10x+6x-15=2x3-x2-4x-15
随堂检测
4.先化简,再求值:,其中.
解:原式
,
当时,
原式.
随堂检测
解:因为(x+4)(x-6)=x2-6x+4x-24=x2-2x-24,
所以x2-2x-24=x2+ax+b,
因此a=-2,b=-24.
所以a2+ab=(-2)2+(-2)×(-24)=4+48=52.
1.若(x+4)(x-6)=x2+ax+b,求a2+ab的值.
能力提升
2.若(x2+mx+8)(x2﹣3x+n)的展开式中不含x3和x2的项,求mn的值.
解:(x2+mx+8)(x2-3x+n)
=x4﹣3x3+nx2+mx3﹣3mx2+mnx+8x2﹣24x+8n
=x4+(m﹣3)x3+(n﹣3m+8)x2+(mn﹣24)x+8n,
∵展开式中不含x3和x2的项,
∴ ,
解得:m=3,n=1,
∴mn=3×1=3.
能力提升
(a+b)( p+q)=ap+aq+bp+bq
(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
推广:
注意:多项式与多项式相乘时,要按照一定的顺序进行,做到不重不漏.
课堂小结
1.计算(x+1)(x+2)的结果为( )
A.x2+2 B.x2+3x+2 C.x2+3x+3 D.x2+2x+2
2.下列多项式相乘的结果为x2+3x-18的是( )
A. (x-2)(x+9) B. (x+2)(x-9) C. (x+3)(x-6) D. (x-3)(x+6)
3.若(x+3)(x+n)=x2+mx-15,则m的值为( )
A.-5 B.5 C.-2 D.2
4.已知(x-2)(x2+mx+n)的乘积项中不含x2和x项, 则m,n的值分别为( )
A. m=2,n=4 B. m=3, n=6 C. m=-2,n=-4 D. m=-3,n=-6
B
D
C
A
课后作业
5.计算:
(1) (2x+3y) (x -2y) (2) (-2a+3) (5+a)
(3) (-3m+2)2 (4) (m+2) (2m2-m-3)
解: (1)原式=2x2-4xy+3xy-6y2=2x2-xy-6y2
(2)原式=-10a-2a2+15+3a=-2a2-7a+15
(3)原式=(-3m+2)(-3m+2)=9m2-6m-6m+4=9m2-12m+4
(4)原式=2m3-m2-3m+4m2-2m-6=2m3-m2+4m2-3m-2m-6
=2m3+3m2-5m-6
课后作业
主讲:
人教版八年级数学上册
感谢聆听
14.1.4 整式的乘法(第3课时)
主讲:
人教版数学八年级上册
第十四章 整式的乘法
与因式分解
1.探索并了解多项式与多项式相乘的法则,并运用它们进行运算.
2.让学生主动参与到探索过程中去,逐步形成独立思考、主动探索的习惯,培养思维的批判性、严密性和初步解决问题的能力.
学习目标
1.如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项,
2.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.
复习引入
计算:1.单项式乘以单项式
2.单项式乘以多项式
(-3x)·(x2+4x);
解:原式=(-3x)·(x2)+(-3x)·4x
=-3x3-12x2;
(-4ab)·3a2bc;
解:原式=(-4×3)·(a·a2)·(b·b)·c
=-12a3b2c;
复习引入
问题3 如图,为了扩大街心花园的绿地面积,把一块原长a米,宽p米的长方形绿地,增长了b米,加宽了q米.你能用几种方法求出扩大后的绿地的面积
p
q
a
b
ap
bq
bp
aq
新知探究
p
q
a
b
ap
bq
bp
aq
解法一:扩大后的绿地面积可以看成长为(a+b)m,宽为(p+q)m的长方形,所以这块绿地的面积为
(a+b)(p+q) ①
解法二:扩大后的绿地面积还可以看成由四个小长方形组成,所以这块绿地的面积为
ap+aq+bp+bq ②
新知探究
由于①和②表示同一个量,所以:
(a+b)(p+q)=ap+aq+bp+bq
多项式
多项式
思考:观察式子(a+b)(p+q)=ap+aq+bp+bq 的特征,你能说出多项式与多项式相乘的法则吗?
把p+q看做一个整体,运用单项式与多项式相乘的法则,得
(a+b)(p+q)=a(p+q)+b(p+q).
新知探究
再利用单项式与多项式相乘的法则,得
a(p+q)+b(p+q)=ap+aq+bp+bq.
总体上看,(a+b)(p+q)的结果可以看作由a+b的每一项乘p+q的每一项,再把所得的积相加而得到的,
即
(a+b)(p+q)=ap+aq+bp+bq
新知探究
(a+b)( p+q)=ap+aq+bp+bq
(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
推广:
注意:多项式与多项式相乘时,要按照一定的顺序进行,做到不重不漏.
新知探究
多项式与多项式相乘的步骤:
(1) 先用一个多项式的每一项分别乘以另一个多项式的每一项;
(2) 把各乘积相加;
(3) 有同类项的要合并同类项;
(4) 通常把结果整理成按某一字母的降幂排列.
总结归纳
例6 计算:
(1)(3x+1)(x+2); (2)(x-8y)(x-y);
(3) (x+y)(x2-xy+y2).
解:(1)原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(2) 原式=x·x+x·(-y)+(-8y)·x+(-8y)·(-y)
=x·x-xy-8xy+8y2
=x2-9xy+8y2;
结果中有同类项的要合并同类项.
计算时要注意符号问题.
典例精析
例6 计算:
(3) (x+y)(x2-xy+y2).
(3)原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
=x3+y3.
计算时不能漏乘.
需要注意的几个问题:(1)漏乘;
(2)符号问题;
(3)最后结果应化成最简形式.
典例精析
1.下列多项式相乘结果为a2-3a-18的是( )
A.(a-2)(a+9) B.(a+2)(a-9)
C.(a+3)(a-6) D.(a-3)(a+6)
2.下列各式中错误的是( )
A.(2a+3)(2a-3)=4a2-9
B.(3a+4b)2=9a2+24ab+4b2
C.(x+2)(x-10)=x2-8x-20
D.(x+y)(x2-xy+y2)=x3+y3
C
B
随堂检测
3.计算:
(1)(2x+1)(x+3) (2)(m+2n)(3n-m) (3)(a-1)2
(4)(a+3b)(a-3b) (5)(2x2-1)(x-4) (6)(x2+2x+3)(2x-5)
解:(1)原式=2x2+6x+x+3=2x2+7x+3
(2)原式=3mn-m2+6n2-2mn=mn-m2+6n2
(3)原式=(a-1)(a-1)=a2-a-a+1=a2-2a+1
(4)原式=a2-3ab+3ab-9b2=a2-9b2
(5)原式=2x2-8x2-x+4
(6)原式=2x3-5x2+4x2-10x+6x-15=2x3-x2-4x-15
随堂检测
4.先化简,再求值:,其中.
解:原式
,
当时,
原式.
随堂检测
解:因为(x+4)(x-6)=x2-6x+4x-24=x2-2x-24,
所以x2-2x-24=x2+ax+b,
因此a=-2,b=-24.
所以a2+ab=(-2)2+(-2)×(-24)=4+48=52.
1.若(x+4)(x-6)=x2+ax+b,求a2+ab的值.
能力提升
2.若(x2+mx+8)(x2﹣3x+n)的展开式中不含x3和x2的项,求mn的值.
解:(x2+mx+8)(x2-3x+n)
=x4﹣3x3+nx2+mx3﹣3mx2+mnx+8x2﹣24x+8n
=x4+(m﹣3)x3+(n﹣3m+8)x2+(mn﹣24)x+8n,
∵展开式中不含x3和x2的项,
∴ ,
解得:m=3,n=1,
∴mn=3×1=3.
能力提升
(a+b)( p+q)=ap+aq+bp+bq
(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
推广:
注意:多项式与多项式相乘时,要按照一定的顺序进行,做到不重不漏.
课堂小结
1.计算(x+1)(x+2)的结果为( )
A.x2+2 B.x2+3x+2 C.x2+3x+3 D.x2+2x+2
2.下列多项式相乘的结果为x2+3x-18的是( )
A. (x-2)(x+9) B. (x+2)(x-9) C. (x+3)(x-6) D. (x-3)(x+6)
3.若(x+3)(x+n)=x2+mx-15,则m的值为( )
A.-5 B.5 C.-2 D.2
4.已知(x-2)(x2+mx+n)的乘积项中不含x2和x项, 则m,n的值分别为( )
A. m=2,n=4 B. m=3, n=6 C. m=-2,n=-4 D. m=-3,n=-6
B
D
C
A
课后作业
5.计算:
(1) (2x+3y) (x -2y) (2) (-2a+3) (5+a)
(3) (-3m+2)2 (4) (m+2) (2m2-m-3)
解: (1)原式=2x2-4xy+3xy-6y2=2x2-xy-6y2
(2)原式=-10a-2a2+15+3a=-2a2-7a+15
(3)原式=(-3m+2)(-3m+2)=9m2-6m-6m+4=9m2-12m+4
(4)原式=2m3-m2-3m+4m2-2m-6=2m3-m2+4m2-3m-2m-6
=2m3+3m2-5m-6
课后作业
主讲:
人教版八年级数学上册
感谢聆听
