24.2点和圆、直线和圆的位置关系同步练习(含解析)
文档属性
| 名称 | 24.2点和圆、直线和圆的位置关系同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览


文档简介
24.2 点和圆、直线和圆的位置关系同步练习
2024-2025学年九年级人教版数学
一、单选题
1.在⊙O中,半径为5,圆心O在坐标原点上,点P的坐标为,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.不能确定
2.如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. B. C.5 D.5
3.如图,是锐角三角形的外接圆,,垂足分别为,连接.若的周长为21,则的长为( )
A.8 B.4 C.3.5 D.3
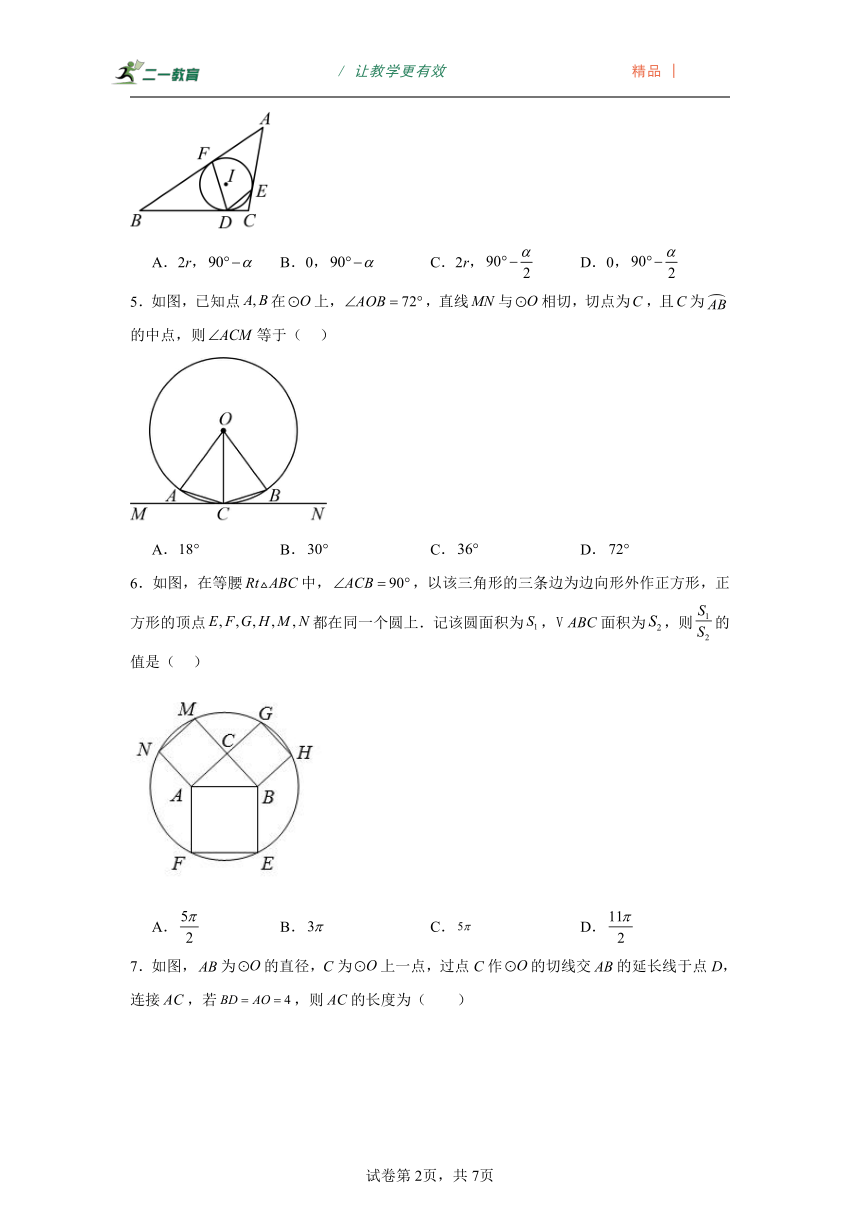
4.如图,的内切圆与,,分别相切于点D,E,F,若的半径为r,,则的值和的大小分别为( )
A.2r, B.0, C.2r, D.0,
5.如图,已知点在上,,直线与相切,切点为,且为的中点,则等于( )
A. B. C. D.
6.如图,在等腰中,,以该三角形的三条边为边向形外作正方形,正方形的顶点都在同一个圆上.记该圆面积为,面积为,则的值是( )
A. B. C. D.
7.如图,为的直径,C为上一点,过点C作的切线交的延长线于点D,连接,若,则的长度为( )
A. B. C.8 D.
8.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,则该弧的圆心的坐标为( )
A.(1,0) B.(2,0) C.(2.5,0) D.(2.5,1)
9.如图,在四边形材料中, ,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A. B. C. D.
10.如图,,是的切线,切点为A,D,点B,C在上,若,则( )
A. B. C. D.
二、填空题
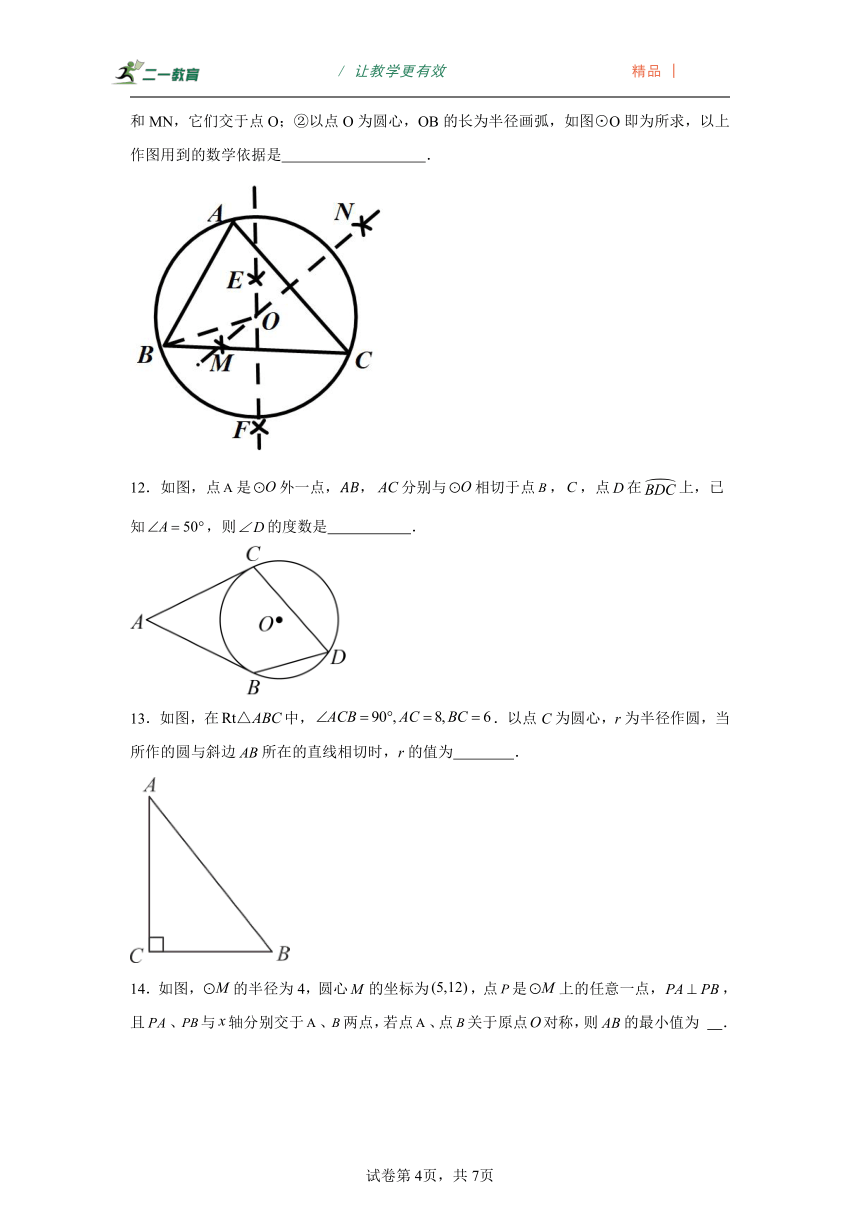
11.已知:,求作的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是 .
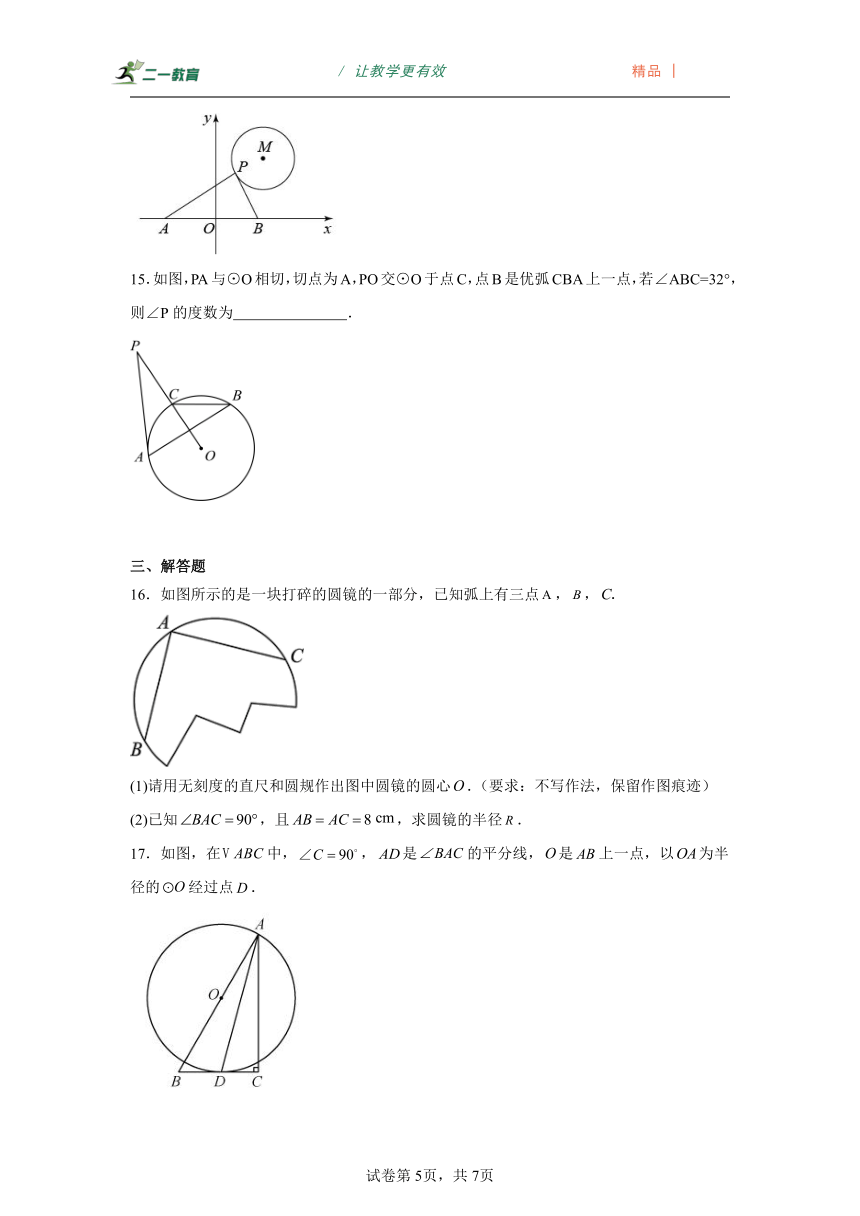
12.如图,点是外一点,,分别与相切于点,,点在上,已知,则的度数是 .
13.如图,在中,.以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为 .
14.如图,的半径为4,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最小值为 .
15.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
三、解答题
16.如图所示的是一块打碎的圆镜的一部分,已知弧上有三点,,
(1)请用无刻度的直尺和圆规作出图中圆镜的圆心.(要求:不写作法,保留作图痕迹)
(2)已知,且,求圆镜的半径.
17.如图,在中,,是的平分线,是上一点,以为半径的经过点.
(1)求证:是切线;
(2)若,,求的长.
18.(1)课本再现:在中,是所对的圆心角,是所对的圆周角,我们在数学课上探索两者之间的关系时,要根据圆心O与的位置关系进行分类.图1是其中一种情况,请你在图2和图3中画出其它两种情况的图形,并从三种位置关系中任选一种情况证明;
(2)知识应用:如图4,若的半径为2,分别与相切于点A,B,,求的长.
19.如图,以线段为直径作,交射线于点,平分交于点,过点作直线于点,交的延长线于点.连接并延长交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的长.
20.如图,在中,,以为直径的交边于点,连接,过点作.
(1)请用无刻度的直尺和圆规作图:过点作的切线,交于点;(不写作法,保留作图痕迹,标明字母)
(2)在(1)的条件下,求证:.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】先根据勾股定理求出的长,再与的半径为5相比较即可.
【详解】解:的坐标为,
,
的半径为5,
点P在上.
故选:B.
【点睛】本题考查点与圆的位置关系,坐标与图形的性质等知识,解题的关键是熟知点与圆的三种位置关系.
2.C
【分析】先利用切线长定理得到PA=PB,再利用∠APB=60°可判断△APB为等边三角形,然后根据等边三角形的性质求解.
【详解】解:∵PA,PB为⊙O的切线,
∴PA=PB,
∵∠APB=60°,
∴△APB为等边三角形,
∴AB=PA=5.
故选:C.
【点睛】本题考查了切线长定理以及等边三角形的判定与性质.此题比较简单,注意掌握数形结合思想的应用.
3.B
【分析】根据三角形外接圆的性质得出点D、E、F分别是的中点,再由中位线的性质及三角形的周长求解即可.
【详解】解:∵是锐角三角形的外接圆,,
∴点D、E、F分别是的中点,
∴,
∵的周长为21,
∴即,
∴,
故选:B.
【点睛】题目主要考查三角形外接圆的性质及中位线的性质,理解题意,熟练掌握三角形外接圆的性质是解题关键.
4.D
【分析】如图,连接.利用切线长定理,圆周角定理,切线的性质解决问题即可.
【详解】解:如图,连接.
∵的内切圆与,,分别相切于点D,E,F,
∴,
∴,,
∴,
∴.
故选:D.
【点睛】本题考查三角形的内切圆与内心,圆周角定理,切线的性质等知识,解题的关键是掌握切线的性质,属于中考常考题型.
5.A
【分析】本题考查了切线的性质,三角形内角和以及等腰三角形的性质,根据C为的中点,三角形内角和可求出,再根据切线的性质即可求解.
【详解】∵,为的中点,
∴
∵
∴
∵直线与相切,
∴,
∴
故选:A.
6.C
【分析】先确定圆的圆心在直角三角形斜边的中点,然后利用全等三角形的判定和性质确定△ABC是等腰直角三角形,再根据直角三角形斜边中线的性质得到,再由勾股定理解得,解得,据此解题即可.
【详解】解:如图所示,正方形的顶点都在同一个圆上,
圆心在线段的中垂线的交点上,即在斜边的中点,且AC=MC,BC=CG,
∴AG=AC+CG=AC+BC,BM=BC+CM=BC+AC,
∴AG=BM,
又∵OG=OM,OA=OB,
∴△AOG≌△BOM,
∴∠CAB=∠CBA,
∵∠ACB=90°,
∴∠CAB=∠CBA=45°,
,
,
.
故选:C.
【点睛】本题考查勾股定理、直角三角形斜边的中线的性质、圆的面积、三角形的面积等知识,是重要考点,难度一般,掌握相关知识是解题关键.
7.D
【分析】连接,根据切线的定义得出,推出,根据勾股定理得出,进而得出,根据圆周角定理得出,即可求解.
【详解】解:如图,连接,
∵为的切线,
∴,
∵,
∴,,
∴,
由圆周角定理得:,
∴,
∴,
故选:D.
【点睛】本题主要考查了切线的定义,勾股定理,圆周角定理,等腰三角形的性质,解题的关键是掌握相关知识点并熟练运用.
8.B
【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦和的垂直平分线,交点即为圆心.
【详解】解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦和的垂直平分线,交点即为圆心.
如图所示,则圆心是.
故选:B.
【点睛】本题考查垂径定理的应用,解题的关键是熟知垂径定理,即“垂直于弦的直径平分弦”.
9.B
【分析】如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,据此求解即可.
【详解】解:如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,
∵,∠BAD=90°,
∴△EAD∽△EBC,∠B=90°,
∴,即,
∴,
∴EB=32cm,
∴,
设这个圆的圆心为O,与EB,BC,EC分别相切于F,G,H,
∴OF=OG=OH,
∵,
∴,
∴,
∴,
∴此圆的半径为8cm,
故选B.
【点睛】
本题主要考查了三角形内切圆半径与三角形三边的关系,勾股定理,正确作出辅助线是解题的关键.
10.C
【分析】本题考查了圆的内接四边形的性质,切线长定理,等腰三角形的性质等知识点,正确作辅助线是解题关键.
根据圆的内接四边形的性质得,由得,由切线长定理得,即可求得结果.
【详解】解:如图,连接,
∵四边形是的内接四边形,
∴,
∵,
∴,
即,
∴,
∵,是的切线,根据切线长定理得,
∴,
∴,
∴.
故选:C.
11.线段的垂直平分线的性质
【分析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
【详解】解:如图,连接,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为的外接圆.
故答案为:线段的垂直平分线的性质.
【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.考查线段的垂直平分线的性质,确定圆的条件,掌握作图的原理是解题的关键.
12./度
【分析】连接,根据切线的性质得出,根据四边形内角和得出,根据圆周角定理即可求解.
【详解】解:如图,
∵,分别与相切于点,,
∴,
∵,
∴,
∵,
∴,
故答案为:.
【点睛】本题考查了切线的性质,圆周角定理,求得是解题的关键.
13.
【分析】根据勾股定理,得,根据切线的性质,得到圆的半径等于边上的高,根据直角三角形的面积不变性计算即可.
【详解】∵,
∴,
根据切线的性质,得到圆的半径等于边上的高,
∴,
∴,
故答案为:.
【点睛】本题考查了勾股定理,切线的性质,熟练掌握勾股定理,切线的性质是解题的关键.
14.18
【分析】由中知要使取得最小值,则需取得最小值,连接,交于点,当点位于位置时,取得最小值,据此求解可得.
【详解】解:连接,
,
,
,
,
若要使取得最小值,则需取得最小值,
连接,交于点,当点位于位置时,取得最小值,
过点作轴于点,
则,,
,
又,
,
,
故答案是:18.
【点睛】本题主要考查点与圆的位置关系,解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB取得最小值时点P的位置.
15.26°
【分析】连接OA,则△PAO是直角三角形,根据圆周角定理即可求得∠POA的度数,进而根据直角三角形的性质求解.
【详解】解:连接OA.
∴∠PAO=90°,
∵∠O=2∠B=64°,
∴∠P=90°-64°=26°.
故答案为:26°.
【点睛】本题主要考查了切线的性质,以及圆周角定理,正确利用定理,作出辅助线求得∠POA的度数是解题的关键.
16.(1)见解析
(2)
【分析】(1)作的垂直平分线交于点,则点即为所求;
(2)连接,根据直角所对的弦是直径,根据勾股定理求得,进而即可求解.
【详解】(1)解:如图所示,
点即为所求;
(2)如图所示,连接,
∵,
∴是的直径,
在中,,
∴,
∴圆镜的半径
【点睛】本题考查了确定圆心,作垂直平分线,直角所对的弦是直径,勾股定理,掌握以上知识是解题的关键.
17.(1)见解析
(2)
【分析】(1)连接,根据圆周角定理和角平分线平分角,易证,得到,得到,从而得到,即可得出结论;
(2)过点作,可得,利用所对的直角边是斜边的一半,以及勾股定理,求出的长,进而求出的长,利用所对的直角边是斜边的一半,求出的长,进而求出的长,再用勾股定理求出即可.
【详解】(1)解:连接,
∵,
∴
∴,
∵是的平分线,
∴,
∴,
∴,
∴,
∴,
∴是切线;
(2)解:过点作,交于点,
∵是的平分线,,
∴,
∵,
∴,
∴,
∵,
∴,
∴或(舍掉),
∴,
∴,
∴,
∴.
【点睛】本题考查切线的判定,角平分线的性质,含的直角三角形以及勾股定理.熟练掌握切线的判定方法,角平分线上的点到角两边的距离相等,是解题的关键.
18.(1)见解析;(2)
【分析】(1)①如图2,当点O在∠ACB的内部,作直径,根据三角形外角的性质和等腰三角形的性质可得结论;②如图3,当O在∠ACB的外部时,作直径CD,同理可理结论;
(2)如图4,先根据(1)中的结论可得∠AOB=120°,由切线的性质可得∠OAP=∠OBP=90°,可得∠OPA=30°,从而得PA的长.
【详解】解:(1)①如图2,连接CO,并延长CO交⊙O于点D,
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO,
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB,
∴∠ACB=∠AOB;
如图3,连接CO,并延长CO交⊙O于点D,
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO,
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD-∠BOD=2∠ACO-2∠BCO=2∠ACB,
∴∠ACB=∠AOB;
(2)如图4,连接OA,OB,OP,
∵∠C=60°,
∴∠AOB=2∠C=120°,
∵PA,PB分别与⊙O相切于点A,B,
∴∠OAP=∠OBP=90°,∠APO=∠BPO=∠APB=(180°-120°)=30°,
∵OA=2,
∴OP=2OA=4,
∴PA=
【点睛】本题考查了切线长定理,圆周角定理等知识,掌握证明圆周角定理的方法是解本题的关键.
19.(1)见解析
(2)见解析
(3)
【分析】(1)连接OD,由∠ODA=∠OAD=∠DAC证明ODAC,得∠ODF=∠AED=90°,即可证明直线DE是⊙O的切线;
(2)由线段AB是⊙O的直径证明∠ADB=90°,再根据等角的余角相等证明∠M=∠ABM,则AB=AM;
(3)由∠AEF=90°,∠F=30°证明∠BAM=60°,则△ABM是等边三角形,所以∠M=60°,则∠EDM=30°,所以BD=MD=2ME=2,再证明∠BDF=∠F,得BF=BD=2.
【详解】(1)证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴ODAC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)证明:线段是的直径,
,
∴∠ADM=180°-∠ADB=,
∴∠M+∠DAM=,∠ABM+∠DAB=,
∵∠DAM=∠DAB,
∴∠M=∠ABM,
∴AB=AM.
(3)解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,
∴∠M=60°,
∵∠DEM=90°,ME=1,
∴∠EDM=30°,
∴MD=2ME=2,
∴BD=MD=2,
∵∠BDF=∠EDM=30°,
∴∠BDF=∠F,
∴BF=BD=2.
【点睛】此题重点考查切线的判定、直径所对的圆周角是直角、等角的余角相等、等腰三角形的判定与性质、等边三角形的判定与性质、平行线的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半等知识,正确地作出所需要的辅助线是解题的关键.
20.(1)见解析
(2)见解析
【分析】(1)根据尺规作图,过点作的垂线,交于点,即可求解;
(2)根据题意切线的性质以及直径所对的圆周角是直角,证明,根据平行线的性质以及等腰三角形的性质得出,进而证明,即可得证.
【详解】(1)解:方法不唯一,如图所示.
(2)∵,
∴.
又∵,
∴,
∴.
∵点在以为直径的圆上,
∴,
∴.
又∵为的切线,
∴.
∵,
∴,
∴,
∴.
∵在和中,
∴.
∴.
【点睛】本题考查了作圆的切线,切线的性质,直径所对的圆周角是直角,全等三角形的性质与判定,熟练掌握以上知识是解题的关键.
答案第1页,共2页
答案第1页,共2页
2024-2025学年九年级人教版数学
一、单选题
1.在⊙O中,半径为5,圆心O在坐标原点上,点P的坐标为,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.不能确定
2.如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. B. C.5 D.5
3.如图,是锐角三角形的外接圆,,垂足分别为,连接.若的周长为21,则的长为( )
A.8 B.4 C.3.5 D.3
4.如图,的内切圆与,,分别相切于点D,E,F,若的半径为r,,则的值和的大小分别为( )
A.2r, B.0, C.2r, D.0,
5.如图,已知点在上,,直线与相切,切点为,且为的中点,则等于( )
A. B. C. D.
6.如图,在等腰中,,以该三角形的三条边为边向形外作正方形,正方形的顶点都在同一个圆上.记该圆面积为,面积为,则的值是( )
A. B. C. D.
7.如图,为的直径,C为上一点,过点C作的切线交的延长线于点D,连接,若,则的长度为( )
A. B. C.8 D.
8.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,则该弧的圆心的坐标为( )
A.(1,0) B.(2,0) C.(2.5,0) D.(2.5,1)
9.如图,在四边形材料中, ,,,,.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A. B. C. D.
10.如图,,是的切线,切点为A,D,点B,C在上,若,则( )
A. B. C. D.
二、填空题
11.已知:,求作的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是 .
12.如图,点是外一点,,分别与相切于点,,点在上,已知,则的度数是 .
13.如图,在中,.以点C为圆心,r为半径作圆,当所作的圆与斜边所在的直线相切时,r的值为 .
14.如图,的半径为4,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最小值为 .
15.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
三、解答题
16.如图所示的是一块打碎的圆镜的一部分,已知弧上有三点,,
(1)请用无刻度的直尺和圆规作出图中圆镜的圆心.(要求:不写作法,保留作图痕迹)
(2)已知,且,求圆镜的半径.
17.如图,在中,,是的平分线,是上一点,以为半径的经过点.
(1)求证:是切线;
(2)若,,求的长.
18.(1)课本再现:在中,是所对的圆心角,是所对的圆周角,我们在数学课上探索两者之间的关系时,要根据圆心O与的位置关系进行分类.图1是其中一种情况,请你在图2和图3中画出其它两种情况的图形,并从三种位置关系中任选一种情况证明;
(2)知识应用:如图4,若的半径为2,分别与相切于点A,B,,求的长.
19.如图,以线段为直径作,交射线于点,平分交于点,过点作直线于点,交的延长线于点.连接并延长交于点.
(1)求证:直线是的切线;
(2)求证:;
(3)若,,求的长.
20.如图,在中,,以为直径的交边于点,连接,过点作.
(1)请用无刻度的直尺和圆规作图:过点作的切线,交于点;(不写作法,保留作图痕迹,标明字母)
(2)在(1)的条件下,求证:.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】先根据勾股定理求出的长,再与的半径为5相比较即可.
【详解】解:的坐标为,
,
的半径为5,
点P在上.
故选:B.
【点睛】本题考查点与圆的位置关系,坐标与图形的性质等知识,解题的关键是熟知点与圆的三种位置关系.
2.C
【分析】先利用切线长定理得到PA=PB,再利用∠APB=60°可判断△APB为等边三角形,然后根据等边三角形的性质求解.
【详解】解:∵PA,PB为⊙O的切线,
∴PA=PB,
∵∠APB=60°,
∴△APB为等边三角形,
∴AB=PA=5.
故选:C.
【点睛】本题考查了切线长定理以及等边三角形的判定与性质.此题比较简单,注意掌握数形结合思想的应用.
3.B
【分析】根据三角形外接圆的性质得出点D、E、F分别是的中点,再由中位线的性质及三角形的周长求解即可.
【详解】解:∵是锐角三角形的外接圆,,
∴点D、E、F分别是的中点,
∴,
∵的周长为21,
∴即,
∴,
故选:B.
【点睛】题目主要考查三角形外接圆的性质及中位线的性质,理解题意,熟练掌握三角形外接圆的性质是解题关键.
4.D
【分析】如图,连接.利用切线长定理,圆周角定理,切线的性质解决问题即可.
【详解】解:如图,连接.
∵的内切圆与,,分别相切于点D,E,F,
∴,
∴,,
∴,
∴.
故选:D.
【点睛】本题考查三角形的内切圆与内心,圆周角定理,切线的性质等知识,解题的关键是掌握切线的性质,属于中考常考题型.
5.A
【分析】本题考查了切线的性质,三角形内角和以及等腰三角形的性质,根据C为的中点,三角形内角和可求出,再根据切线的性质即可求解.
【详解】∵,为的中点,
∴
∵
∴
∵直线与相切,
∴,
∴
故选:A.
6.C
【分析】先确定圆的圆心在直角三角形斜边的中点,然后利用全等三角形的判定和性质确定△ABC是等腰直角三角形,再根据直角三角形斜边中线的性质得到,再由勾股定理解得,解得,据此解题即可.
【详解】解:如图所示,正方形的顶点都在同一个圆上,
圆心在线段的中垂线的交点上,即在斜边的中点,且AC=MC,BC=CG,
∴AG=AC+CG=AC+BC,BM=BC+CM=BC+AC,
∴AG=BM,
又∵OG=OM,OA=OB,
∴△AOG≌△BOM,
∴∠CAB=∠CBA,
∵∠ACB=90°,
∴∠CAB=∠CBA=45°,
,
,
.
故选:C.
【点睛】本题考查勾股定理、直角三角形斜边的中线的性质、圆的面积、三角形的面积等知识,是重要考点,难度一般,掌握相关知识是解题关键.
7.D
【分析】连接,根据切线的定义得出,推出,根据勾股定理得出,进而得出,根据圆周角定理得出,即可求解.
【详解】解:如图,连接,
∵为的切线,
∴,
∵,
∴,,
∴,
由圆周角定理得:,
∴,
∴,
故选:D.
【点睛】本题主要考查了切线的定义,勾股定理,圆周角定理,等腰三角形的性质,解题的关键是掌握相关知识点并熟练运用.
8.B
【分析】根据垂径定理的推论:弦的垂直平分线必过圆心,可以作弦和的垂直平分线,交点即为圆心.
【详解】解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦和的垂直平分线,交点即为圆心.
如图所示,则圆心是.
故选:B.
【点睛】本题考查垂径定理的应用,解题的关键是熟知垂径定理,即“垂直于弦的直径平分弦”.
9.B
【分析】如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,据此求解即可.
【详解】解:如图所示,延长BA交CD延长线于E,当这个圆为△BCE的内切圆时,此圆的面积最大,
∵,∠BAD=90°,
∴△EAD∽△EBC,∠B=90°,
∴,即,
∴,
∴EB=32cm,
∴,
设这个圆的圆心为O,与EB,BC,EC分别相切于F,G,H,
∴OF=OG=OH,
∵,
∴,
∴,
∴,
∴此圆的半径为8cm,
故选B.
【点睛】
本题主要考查了三角形内切圆半径与三角形三边的关系,勾股定理,正确作出辅助线是解题的关键.
10.C
【分析】本题考查了圆的内接四边形的性质,切线长定理,等腰三角形的性质等知识点,正确作辅助线是解题关键.
根据圆的内接四边形的性质得,由得,由切线长定理得,即可求得结果.
【详解】解:如图,连接,
∵四边形是的内接四边形,
∴,
∵,
∴,
即,
∴,
∵,是的切线,根据切线长定理得,
∴,
∴,
∴.
故选:C.
11.线段的垂直平分线的性质
【分析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
【详解】解:如图,连接,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为的外接圆.
故答案为:线段的垂直平分线的性质.
【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.考查线段的垂直平分线的性质,确定圆的条件,掌握作图的原理是解题的关键.
12./度
【分析】连接,根据切线的性质得出,根据四边形内角和得出,根据圆周角定理即可求解.
【详解】解:如图,
∵,分别与相切于点,,
∴,
∵,
∴,
∵,
∴,
故答案为:.
【点睛】本题考查了切线的性质,圆周角定理,求得是解题的关键.
13.
【分析】根据勾股定理,得,根据切线的性质,得到圆的半径等于边上的高,根据直角三角形的面积不变性计算即可.
【详解】∵,
∴,
根据切线的性质,得到圆的半径等于边上的高,
∴,
∴,
故答案为:.
【点睛】本题考查了勾股定理,切线的性质,熟练掌握勾股定理,切线的性质是解题的关键.
14.18
【分析】由中知要使取得最小值,则需取得最小值,连接,交于点,当点位于位置时,取得最小值,据此求解可得.
【详解】解:连接,
,
,
,
,
若要使取得最小值,则需取得最小值,
连接,交于点,当点位于位置时,取得最小值,
过点作轴于点,
则,,
,
又,
,
,
故答案是:18.
【点睛】本题主要考查点与圆的位置关系,解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB取得最小值时点P的位置.
15.26°
【分析】连接OA,则△PAO是直角三角形,根据圆周角定理即可求得∠POA的度数,进而根据直角三角形的性质求解.
【详解】解:连接OA.
∴∠PAO=90°,
∵∠O=2∠B=64°,
∴∠P=90°-64°=26°.
故答案为:26°.
【点睛】本题主要考查了切线的性质,以及圆周角定理,正确利用定理,作出辅助线求得∠POA的度数是解题的关键.
16.(1)见解析
(2)
【分析】(1)作的垂直平分线交于点,则点即为所求;
(2)连接,根据直角所对的弦是直径,根据勾股定理求得,进而即可求解.
【详解】(1)解:如图所示,
点即为所求;
(2)如图所示,连接,
∵,
∴是的直径,
在中,,
∴,
∴圆镜的半径
【点睛】本题考查了确定圆心,作垂直平分线,直角所对的弦是直径,勾股定理,掌握以上知识是解题的关键.
17.(1)见解析
(2)
【分析】(1)连接,根据圆周角定理和角平分线平分角,易证,得到,得到,从而得到,即可得出结论;
(2)过点作,可得,利用所对的直角边是斜边的一半,以及勾股定理,求出的长,进而求出的长,利用所对的直角边是斜边的一半,求出的长,进而求出的长,再用勾股定理求出即可.
【详解】(1)解:连接,
∵,
∴
∴,
∵是的平分线,
∴,
∴,
∴,
∴,
∴,
∴是切线;
(2)解:过点作,交于点,
∵是的平分线,,
∴,
∵,
∴,
∴,
∵,
∴,
∴或(舍掉),
∴,
∴,
∴,
∴.
【点睛】本题考查切线的判定,角平分线的性质,含的直角三角形以及勾股定理.熟练掌握切线的判定方法,角平分线上的点到角两边的距离相等,是解题的关键.
18.(1)见解析;(2)
【分析】(1)①如图2,当点O在∠ACB的内部,作直径,根据三角形外角的性质和等腰三角形的性质可得结论;②如图3,当O在∠ACB的外部时,作直径CD,同理可理结论;
(2)如图4,先根据(1)中的结论可得∠AOB=120°,由切线的性质可得∠OAP=∠OBP=90°,可得∠OPA=30°,从而得PA的长.
【详解】解:(1)①如图2,连接CO,并延长CO交⊙O于点D,
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO,
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB,
∴∠ACB=∠AOB;
如图3,连接CO,并延长CO交⊙O于点D,
∵OA=OC=OB,
∴∠A=∠ACO,∠B=∠BCO,
∵∠AOD=∠A+∠ACO=2∠ACO,∠BOD=∠B+∠BCO=2∠BCO,
∴∠AOB=∠AOD-∠BOD=2∠ACO-2∠BCO=2∠ACB,
∴∠ACB=∠AOB;
(2)如图4,连接OA,OB,OP,
∵∠C=60°,
∴∠AOB=2∠C=120°,
∵PA,PB分别与⊙O相切于点A,B,
∴∠OAP=∠OBP=90°,∠APO=∠BPO=∠APB=(180°-120°)=30°,
∵OA=2,
∴OP=2OA=4,
∴PA=
【点睛】本题考查了切线长定理,圆周角定理等知识,掌握证明圆周角定理的方法是解本题的关键.
19.(1)见解析
(2)见解析
(3)
【分析】(1)连接OD,由∠ODA=∠OAD=∠DAC证明ODAC,得∠ODF=∠AED=90°,即可证明直线DE是⊙O的切线;
(2)由线段AB是⊙O的直径证明∠ADB=90°,再根据等角的余角相等证明∠M=∠ABM,则AB=AM;
(3)由∠AEF=90°,∠F=30°证明∠BAM=60°,则△ABM是等边三角形,所以∠M=60°,则∠EDM=30°,所以BD=MD=2ME=2,再证明∠BDF=∠F,得BF=BD=2.
【详解】(1)证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴ODAC,
∵DE⊥AC,
∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)证明:线段是的直径,
,
∴∠ADM=180°-∠ADB=,
∴∠M+∠DAM=,∠ABM+∠DAB=,
∵∠DAM=∠DAB,
∴∠M=∠ABM,
∴AB=AM.
(3)解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,
∴∠M=60°,
∵∠DEM=90°,ME=1,
∴∠EDM=30°,
∴MD=2ME=2,
∴BD=MD=2,
∵∠BDF=∠EDM=30°,
∴∠BDF=∠F,
∴BF=BD=2.
【点睛】此题重点考查切线的判定、直径所对的圆周角是直角、等角的余角相等、等腰三角形的判定与性质、等边三角形的判定与性质、平行线的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半等知识,正确地作出所需要的辅助线是解题的关键.
20.(1)见解析
(2)见解析
【分析】(1)根据尺规作图,过点作的垂线,交于点,即可求解;
(2)根据题意切线的性质以及直径所对的圆周角是直角,证明,根据平行线的性质以及等腰三角形的性质得出,进而证明,即可得证.
【详解】(1)解:方法不唯一,如图所示.
(2)∵,
∴.
又∵,
∴,
∴.
∵点在以为直径的圆上,
∴,
∴.
又∵为的切线,
∴.
∵,
∴,
∴,
∴.
∵在和中,
∴.
∴.
【点睛】本题考查了作圆的切线,切线的性质,直径所对的圆周角是直角,全等三角形的性质与判定,熟练掌握以上知识是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
