24.4弧长和扇形面积同步练习(含解析)
文档属性
| 名称 | 24.4弧长和扇形面积同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 773.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 20:05:12 | ||
图片预览



文档简介
24.4弧长和扇形面积同步练习2024-2025学年九年级人教版数学
一、单选题
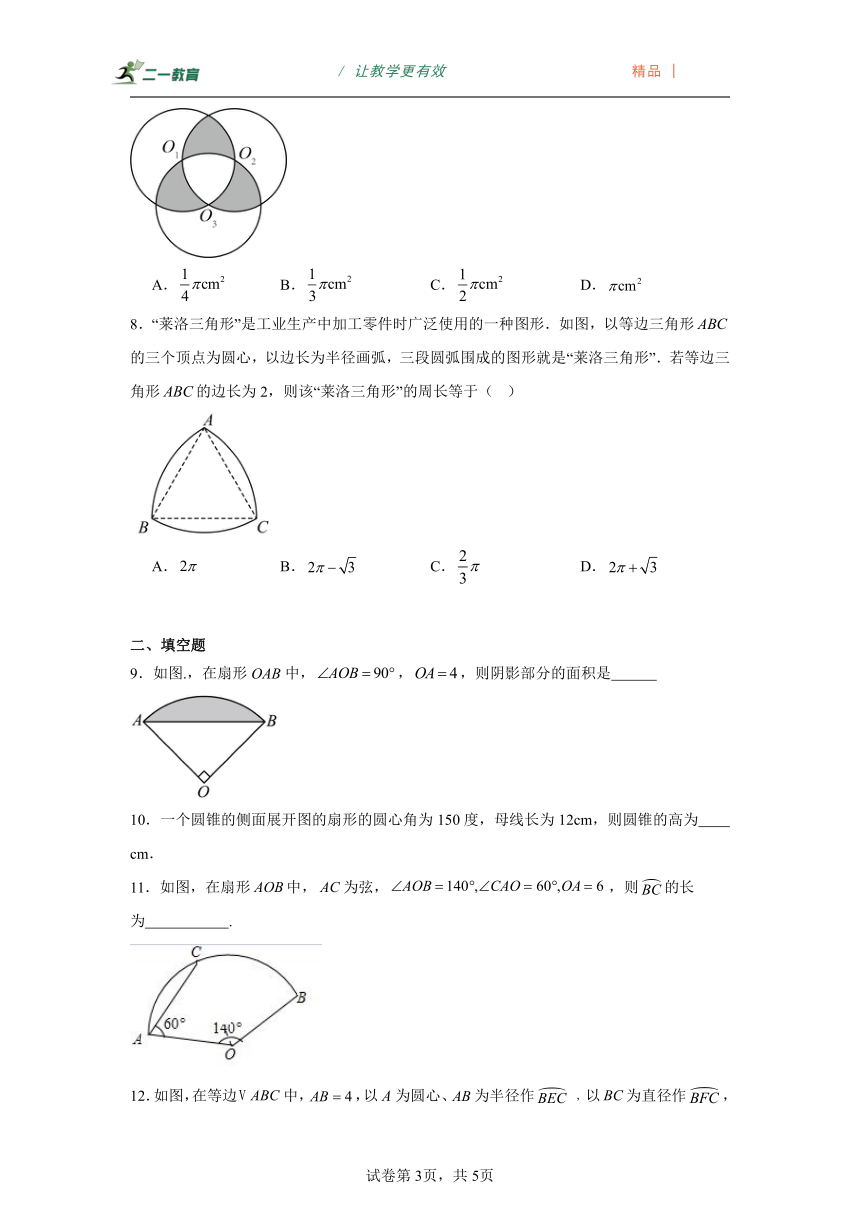
1.如图,,,,,相互外离,它们的半径都是2,顺次连接五个圆心得到五边形,则图中五个扇形(阴影部分)的面积之和是( )
A. B. C. D.
2.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A.6π B.2π C.π D.π
3.如图,半圆的圆心为0,直径AB的长为12,C为半圆上一点,∠CAB=30°,的长是( )
A.12π B.6π C.5π D.4π
4.如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A. B. C. D.
5.如图,在等腰直角三角形中,,点D为的中点,分别以A,B为圆心,的一半为半径画弧,分别交于点E,F,若,则图中阴影部分的面积为( )
A. B. C. D.
6.如图,已知点,是以为直径的半圆的三等分点,的长为,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A. B. C. D.
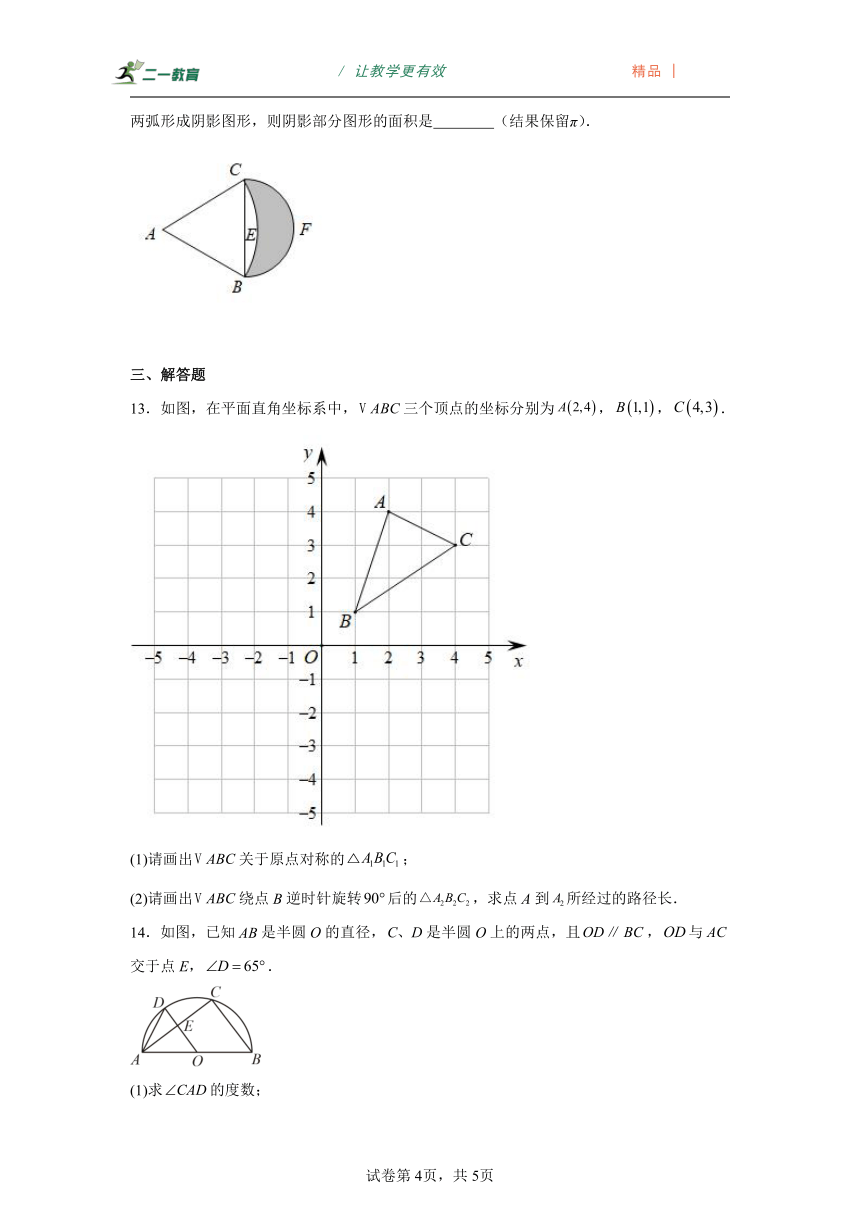
8.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以等边三角形的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”.若等边三角形的边长为2,则该“莱洛三角形”的周长等于( )
A. B. C. D.
二、填空题
9.如图.,在扇形OAB中,,,则阴影部分的面积是
10.一个圆锥的侧面展开图的扇形的圆心角为150度,母线长为12cm,则圆锥的高为 cm.
11.如图,在扇形中,为弦,,则的长为 .
12.如图,在等边中,,以A为圆心、为半径作﹐以为直径作,两弧形成阴影图形,则阴影部分图形的面积是 (结果保留π).
三、解答题
13.如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)请画出关于原点对称的;
(2)请画出绕点B逆时针旋转后的,求点A到所经过的路径长.
14.如图,已知是半圆O的直径,是半圆O上的两点,且,与交于点E,.
(1)求的度数;
(2)若,求的长.
15.如图,装有水的水槽放在水平桌面上,其横截面是以为直径的半圆O,,为桌面截线,水面截线,直径一端点B刚好与点N重合,.
(1)计算的长度,并比较直径与长度的大小;
(2)请在图中画出线段,用其长度表示水的最大深度,并求水的最大深度.
16.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】求出五个扇形的圆心角之和,利用扇形面积公式求解即可.
【详解】
故选A.
【点睛】本题考查了多边形内角和,扇形面积公式,理解题意是解题的关键.
2.D
【分析】先根据圆周角定理求出∠BOC=2∠A=60°,求出半径OB,再根据弧长公式求出答案即可.
【详解】解:∵直径AB=6,
∴半径OB=3,
∵圆周角∠A=30°,
∴圆心角∠BOC=2∠A=60°,
∴的长是=π,
故选:D.
【点睛】本题考查了弧长公式和圆周角定理,能熟记弧长公式是解此题的关键,注意:半径为r,圆心角为n°的弧的长度是.
3.D
【分析】如图,连接OC,利用等腰三角形的性质及内角和定理求得∠AOC的度数,然后利用弧长公式进行解答即可.
【详解】解:如图,连接OC,
∵OA=OC,∠CAB=30°,
∴∠C=∠CAB=30°,
∴∠AOC=120°,
∴弧AC的长度l=.
故选:D.
【点睛】本题考查了弧长的计算,根据题意求得∠AOC的度数是解题的关键.
4.B
【分析】阴影部分的面积等于扇形面积减去三角形面积,分别求出扇形面积和等边三角形的面积即可.
【详解】解:如图,过点OC作OD⊥AB于点D,
∵∠AOB=2×=60°,
∴△OAB是等边三角形,
∴∠AOD=∠BOD=30°,OA=OB=AB=2,AD=BD=AB=1,
∴OD=,
∴阴影部分的面积为,
故选:B.
【点睛】本题考查了扇形面积、等边三角形的面积计算方法,掌握扇形面积、等边三角形的面积的计算方法是正确解答的关键.
5.C
【分析】先根据线段中点的定义可得,再根据勾股定理可得,最后根据阴影部分的面积等于直角三角形的面积减去两个扇形的面积即可解答.
【详解】解:∵点D是线段的中点,,
∴
∵等腰直角三角形中,,
∴,
∴阴影部分面积为:.
故选C.
【点睛】本题主要考查了扇形面积求法、等腰直角三角形的性质,根据题意求得的长是解题的关键.
6.A
【分析】本题考查了扇形面积的计算,连接,,根据,是以为直径的半圆的三等分点,可得,是等边三角形,将阴影部分的面积转化为扇形的面积,根据求解即可.
【详解】解:连接,,,
,是以为直径的半圆的三等分点,
,,
又,
、是等边三角形,
,
,
,
弧的长为,
,
解得:,
.
故选:A.
7.C
【分析】根据圆的对称性可知:图中三个阴影部分的面积相等,只要计算出一个阴影部分的面积即可,如图,连接,阴影的面积=扇形的面积,据此即可解答.
【详解】解:根据圆的对称性可知:图中三个阴影部分的面积相等;
如图,连接,则,是等边三角形,
∴,弓形的面积相等,
∴阴影的面积=扇形的面积,
∴图中三个阴影部分的面积之和;
故选:C.
【点睛】本题考查了不规则图形面积的计算,正确添加辅助线、掌握求解的方法是解题关键.
8.A
【分析】根据等边三角形的性质及弧长公式求解即可.
【详解】解:等边三角形的边长为2,,
,
该“莱洛三角形”的周长,
故选:A.
【点睛】本题考查了等边三角形的性质,弧长公式,熟练掌握知识点是解题的关键.
9./
【分析】根据即可计算.
【详解】解:∵,,
∴是等腰直角三角形,
∴,
故答案为:.
【点睛】本题考查扇形面积公式、三角形面积公式,记住扇形和三角形的面积公式是解题的关键.
10.
【分析】首先求得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.
【详解】解:设圆锥的底面半径为,
则,
解得:,
圆锥的高为,
故答案为:.
【点睛】考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于侧面展开扇形的弧长,难度不大.
11.
【分析】连接OC,判定△OAC为等边三角形,再利用弧长公式计算.
【详解】连接OC,如图所示,
∵OA=OC,∠CAO=60°,
∴△OAC是等边三角形,
∴∠COB=80°,
∵OA=6,
∴的长=,
故答案为: .
【点睛】此题主要考查了学生对等边三角形的判定和弧长公式,关键是得到△OAC是等边三角形.
12.
【分析】先求出扇形、和半圆的面积,再根据阴影的面积=半圆面积(扇形面积面积),即可求.
【详解】过A作于点H,
∵为等边三角形,
∴,
则
∴扇形的面积,
的面积,
半圆面积,
则阴影的面积,
故答案为:.
【点睛】本题考查的是扇形的面积计算,等边三角形的面积,解题的关键是熟练掌握扇形面积公式.
13.(1)见解析
(2)见解析,
【分析】(1)分别作出A,B,C的对应点,,即可.
(2)分别作出A,B,C的对应点,,即可,再利用弧长公式求解即可.
【详解】(1)如图所示即为所求;
(2)如图所示即为所求,
,
点A到经过的路径长.
【点睛】本题考查作图——旋转变换,中心对称,勾股定理和弧长公式,解题的关键是正确得出对应点的位置.
14.(1)
(2)
【分析】(1)根据等腰三角形的性质和三角形内角和定理可求出∠AOD=50°,再根据平行线的性质和等腰三角形的性质可求出∠AOD=∠OBC=∠OCB=∠COD=50°,由圆周角定理可得答案;
(2)根据弧长公式进行计算即可.
【详解】(1)解:如图,连接,
∵,
∴,
∴,
∵,
∴,
∴;
(2)由可得半径为2,,
因此的长为.
【点睛】本题考查等腰三角形的性质,平行线的性质,三角形内角和定理以及圆周角定理,掌握等腰三角形的性质,平行线的性质,三角形内角和定理以及圆周角定理是正确解答的前提.
15.(1)的长度为;直径小于长度
(2)水的最大深度为
【分析】本题主要考查了圆周角定理的推论,垂径定理,含30度角的直角三角形,弧长公式.
(1)连接,由,,求出,根据弧长公式即可求解;
(3)过点O作交于点C,根据含30度角的直角三角形的特征,由,求出,再根据即可得出答案.
【详解】(1)解:如图,连接.
,
,
,
,
,
直径小于长度;
(2)解:如图,过点O作交于点C,
在中,,,
,
,
,
水的最大深度为.
16.(1)AB=AC;(2).
【分析】(1)连接AD,根据圆周角定理可以证得AD垂直且平分BC,然后根据垂直平分线的性质证得AB=AC;
(2)连接OD、过D作DH⊥AB,根据扇形的面积公式解答即可.
【详解】(1)AB=AC.理由是:连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC,
又∵DC=BD,∴AB=AC;
(2)连接OD、过D作DH⊥AB.
∵AB=8,∠BAC=45°,
∴∠BOD=45°,OB=OD=4,
∴DH=2,
∴△OBD的面积=
扇形OBD的面积=,
阴影部分面积=.
【点睛】本题考查了圆周角定理以及等腰三角形的性质定理,理解弧的度数和对应 圆心角的度数的关系是关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,,,,,相互外离,它们的半径都是2,顺次连接五个圆心得到五边形,则图中五个扇形(阴影部分)的面积之和是( )
A. B. C. D.
2.如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠A=30°,则 的长为( )
A.6π B.2π C.π D.π
3.如图,半圆的圆心为0,直径AB的长为12,C为半圆上一点,∠CAB=30°,的长是( )
A.12π B.6π C.5π D.4π
4.如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A. B. C. D.
5.如图,在等腰直角三角形中,,点D为的中点,分别以A,B为圆心,的一半为半径画弧,分别交于点E,F,若,则图中阴影部分的面积为( )
A. B. C. D.
6.如图,已知点,是以为直径的半圆的三等分点,的长为,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,某玩具品牌的标志由半径为的三个等圆构成,且三个等圆相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
A. B. C. D.
8.“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以等边三角形的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”.若等边三角形的边长为2,则该“莱洛三角形”的周长等于( )
A. B. C. D.
二、填空题
9.如图.,在扇形OAB中,,,则阴影部分的面积是
10.一个圆锥的侧面展开图的扇形的圆心角为150度,母线长为12cm,则圆锥的高为 cm.
11.如图,在扇形中,为弦,,则的长为 .
12.如图,在等边中,,以A为圆心、为半径作﹐以为直径作,两弧形成阴影图形,则阴影部分图形的面积是 (结果保留π).
三、解答题
13.如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)请画出关于原点对称的;
(2)请画出绕点B逆时针旋转后的,求点A到所经过的路径长.
14.如图,已知是半圆O的直径,是半圆O上的两点,且,与交于点E,.
(1)求的度数;
(2)若,求的长.
15.如图,装有水的水槽放在水平桌面上,其横截面是以为直径的半圆O,,为桌面截线,水面截线,直径一端点B刚好与点N重合,.
(1)计算的长度,并比较直径与长度的大小;
(2)请在图中画出线段,用其长度表示水的最大深度,并求水的最大深度.
16.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】求出五个扇形的圆心角之和,利用扇形面积公式求解即可.
【详解】
故选A.
【点睛】本题考查了多边形内角和,扇形面积公式,理解题意是解题的关键.
2.D
【分析】先根据圆周角定理求出∠BOC=2∠A=60°,求出半径OB,再根据弧长公式求出答案即可.
【详解】解:∵直径AB=6,
∴半径OB=3,
∵圆周角∠A=30°,
∴圆心角∠BOC=2∠A=60°,
∴的长是=π,
故选:D.
【点睛】本题考查了弧长公式和圆周角定理,能熟记弧长公式是解此题的关键,注意:半径为r,圆心角为n°的弧的长度是.
3.D
【分析】如图,连接OC,利用等腰三角形的性质及内角和定理求得∠AOC的度数,然后利用弧长公式进行解答即可.
【详解】解:如图,连接OC,
∵OA=OC,∠CAB=30°,
∴∠C=∠CAB=30°,
∴∠AOC=120°,
∴弧AC的长度l=.
故选:D.
【点睛】本题考查了弧长的计算,根据题意求得∠AOC的度数是解题的关键.
4.B
【分析】阴影部分的面积等于扇形面积减去三角形面积,分别求出扇形面积和等边三角形的面积即可.
【详解】解:如图,过点OC作OD⊥AB于点D,
∵∠AOB=2×=60°,
∴△OAB是等边三角形,
∴∠AOD=∠BOD=30°,OA=OB=AB=2,AD=BD=AB=1,
∴OD=,
∴阴影部分的面积为,
故选:B.
【点睛】本题考查了扇形面积、等边三角形的面积计算方法,掌握扇形面积、等边三角形的面积的计算方法是正确解答的关键.
5.C
【分析】先根据线段中点的定义可得,再根据勾股定理可得,最后根据阴影部分的面积等于直角三角形的面积减去两个扇形的面积即可解答.
【详解】解:∵点D是线段的中点,,
∴
∵等腰直角三角形中,,
∴,
∴阴影部分面积为:.
故选C.
【点睛】本题主要考查了扇形面积求法、等腰直角三角形的性质,根据题意求得的长是解题的关键.
6.A
【分析】本题考查了扇形面积的计算,连接,,根据,是以为直径的半圆的三等分点,可得,是等边三角形,将阴影部分的面积转化为扇形的面积,根据求解即可.
【详解】解:连接,,,
,是以为直径的半圆的三等分点,
,,
又,
、是等边三角形,
,
,
,
弧的长为,
,
解得:,
.
故选:A.
7.C
【分析】根据圆的对称性可知:图中三个阴影部分的面积相等,只要计算出一个阴影部分的面积即可,如图,连接,阴影的面积=扇形的面积,据此即可解答.
【详解】解:根据圆的对称性可知:图中三个阴影部分的面积相等;
如图,连接,则,是等边三角形,
∴,弓形的面积相等,
∴阴影的面积=扇形的面积,
∴图中三个阴影部分的面积之和;
故选:C.
【点睛】本题考查了不规则图形面积的计算,正确添加辅助线、掌握求解的方法是解题关键.
8.A
【分析】根据等边三角形的性质及弧长公式求解即可.
【详解】解:等边三角形的边长为2,,
,
该“莱洛三角形”的周长,
故选:A.
【点睛】本题考查了等边三角形的性质,弧长公式,熟练掌握知识点是解题的关键.
9./
【分析】根据即可计算.
【详解】解:∵,,
∴是等腰直角三角形,
∴,
故答案为:.
【点睛】本题考查扇形面积公式、三角形面积公式,记住扇形和三角形的面积公式是解题的关键.
10.
【分析】首先求得圆锥的底面半径,然后利用勾股定理求得圆锥的高即可.
【详解】解:设圆锥的底面半径为,
则,
解得:,
圆锥的高为,
故答案为:.
【点睛】考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于侧面展开扇形的弧长,难度不大.
11.
【分析】连接OC,判定△OAC为等边三角形,再利用弧长公式计算.
【详解】连接OC,如图所示,
∵OA=OC,∠CAO=60°,
∴△OAC是等边三角形,
∴∠COB=80°,
∵OA=6,
∴的长=,
故答案为: .
【点睛】此题主要考查了学生对等边三角形的判定和弧长公式,关键是得到△OAC是等边三角形.
12.
【分析】先求出扇形、和半圆的面积,再根据阴影的面积=半圆面积(扇形面积面积),即可求.
【详解】过A作于点H,
∵为等边三角形,
∴,
则
∴扇形的面积,
的面积,
半圆面积,
则阴影的面积,
故答案为:.
【点睛】本题考查的是扇形的面积计算,等边三角形的面积,解题的关键是熟练掌握扇形面积公式.
13.(1)见解析
(2)见解析,
【分析】(1)分别作出A,B,C的对应点,,即可.
(2)分别作出A,B,C的对应点,,即可,再利用弧长公式求解即可.
【详解】(1)如图所示即为所求;
(2)如图所示即为所求,
,
点A到经过的路径长.
【点睛】本题考查作图——旋转变换,中心对称,勾股定理和弧长公式,解题的关键是正确得出对应点的位置.
14.(1)
(2)
【分析】(1)根据等腰三角形的性质和三角形内角和定理可求出∠AOD=50°,再根据平行线的性质和等腰三角形的性质可求出∠AOD=∠OBC=∠OCB=∠COD=50°,由圆周角定理可得答案;
(2)根据弧长公式进行计算即可.
【详解】(1)解:如图,连接,
∵,
∴,
∴,
∵,
∴,
∴;
(2)由可得半径为2,,
因此的长为.
【点睛】本题考查等腰三角形的性质,平行线的性质,三角形内角和定理以及圆周角定理,掌握等腰三角形的性质,平行线的性质,三角形内角和定理以及圆周角定理是正确解答的前提.
15.(1)的长度为;直径小于长度
(2)水的最大深度为
【分析】本题主要考查了圆周角定理的推论,垂径定理,含30度角的直角三角形,弧长公式.
(1)连接,由,,求出,根据弧长公式即可求解;
(3)过点O作交于点C,根据含30度角的直角三角形的特征,由,求出,再根据即可得出答案.
【详解】(1)解:如图,连接.
,
,
,
,
,
直径小于长度;
(2)解:如图,过点O作交于点C,
在中,,,
,
,
,
水的最大深度为.
16.(1)AB=AC;(2).
【分析】(1)连接AD,根据圆周角定理可以证得AD垂直且平分BC,然后根据垂直平分线的性质证得AB=AC;
(2)连接OD、过D作DH⊥AB,根据扇形的面积公式解答即可.
【详解】(1)AB=AC.理由是:连接AD.
∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC,
又∵DC=BD,∴AB=AC;
(2)连接OD、过D作DH⊥AB.
∵AB=8,∠BAC=45°,
∴∠BOD=45°,OB=OD=4,
∴DH=2,
∴△OBD的面积=
扇形OBD的面积=,
阴影部分面积=.
【点睛】本题考查了圆周角定理以及等腰三角形的性质定理,理解弧的度数和对应 圆心角的度数的关系是关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
