24.4弧长和扇形面积同步练习(含解析)
文档属性
| 名称 | 24.4弧长和扇形面积同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 807.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览


文档简介
24.4 弧长和扇形面积同步练习2024-2025学年九年级人教版数学
一、单选题
1.已知圆锥的底面直径为,母线长为,则圆锥的侧面积是( )
A. B. C. D.
2.圆锥的底面圆的半径为1,母线长为3,则它的侧面展开图的圆心角度数为( )
A. B. C. D.
3.如图,已知圆锥的底面圆的半径为3,则这个圆锥的侧面展开图(扇形)的弧长为( )
A. B. C. D.
4.如图,,,两两不相交,且半径都是.则图中三个阴影扇形的弧长之和为( )
A. B. C. D.
5.如图,扇形圆心角为直角,,点在上,以,为邻边构造、边交于点,若,则图中阴影部分的面积为( )
A. B. C. D.
6.如图,已知点,是以为直径的半圆的三等分点,的长为,则图中阴影部分的面积为( )
A. B. C. D.
7.“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若图中阴影部分的面积为,空白部分的面积为,则的值为( )
A. B. C. D.
8.如图,从一个边长是10的正五边形纸片上剪出一个扇形(阴影部分),将剪下来的扇形围成一个圆锥,这个圆锥的底面半径为( )
A.1 B.3 C. D.2
二、填空题
9.一扇形的半径为,圆心角为,则该扇形的弧长为 cm.
10.如图,扇形与扇形的圆心角都是,连接,如果图中阴影部分的面积为,,那么 .
11.如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,以BC为直径作半圆,交AB于点D,则阴影部分的面积是 .
12.如图,扇形的圆心角,半径,点P为扇形内一点,且,延长交于点C,当取最小值时,则图中阴影部分的面积为 .
三、解答题
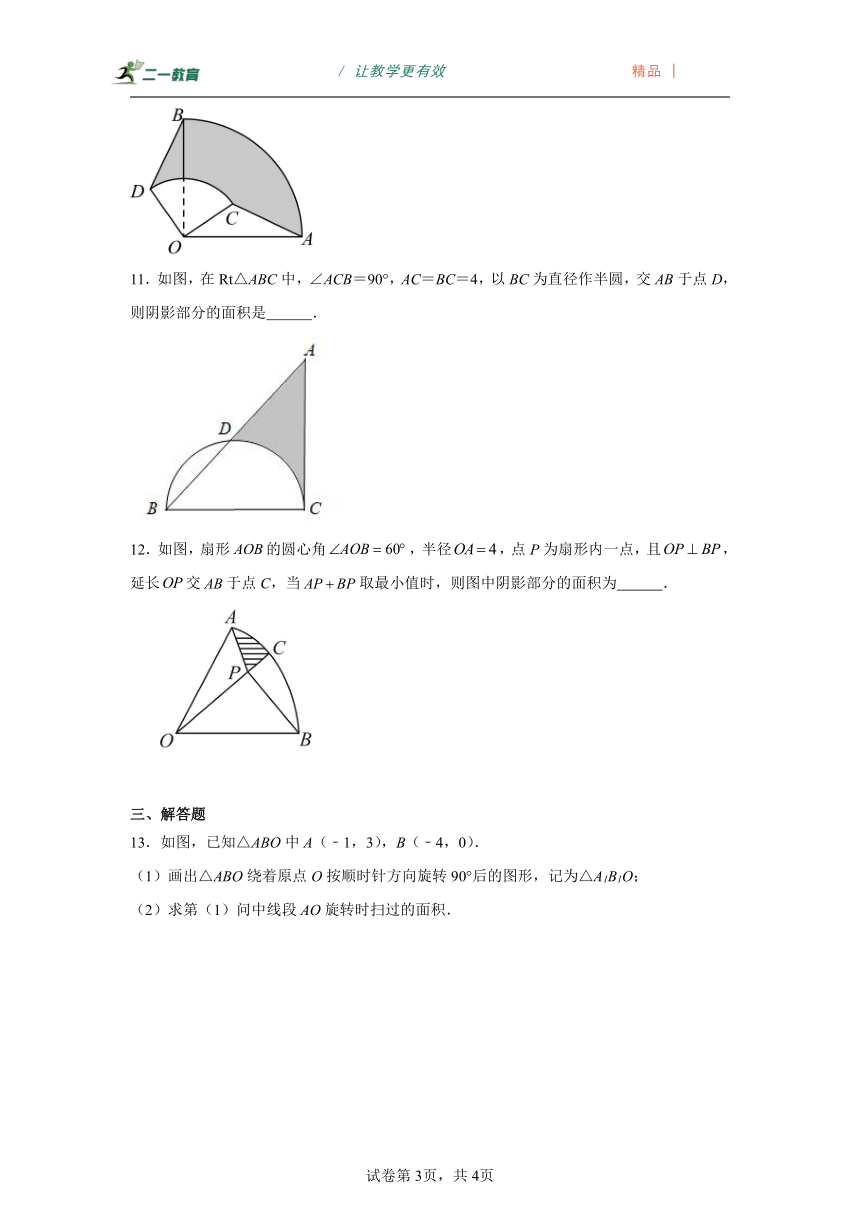
13.如图,已知△ABO中A(﹣1,3),B(﹣4,0).
(1)画出△ABO绕着原点O按顺时针方向旋转90°后的图形,记为△A1B1O;
(2)求第(1)问中线段AO旋转时扫过的面积.
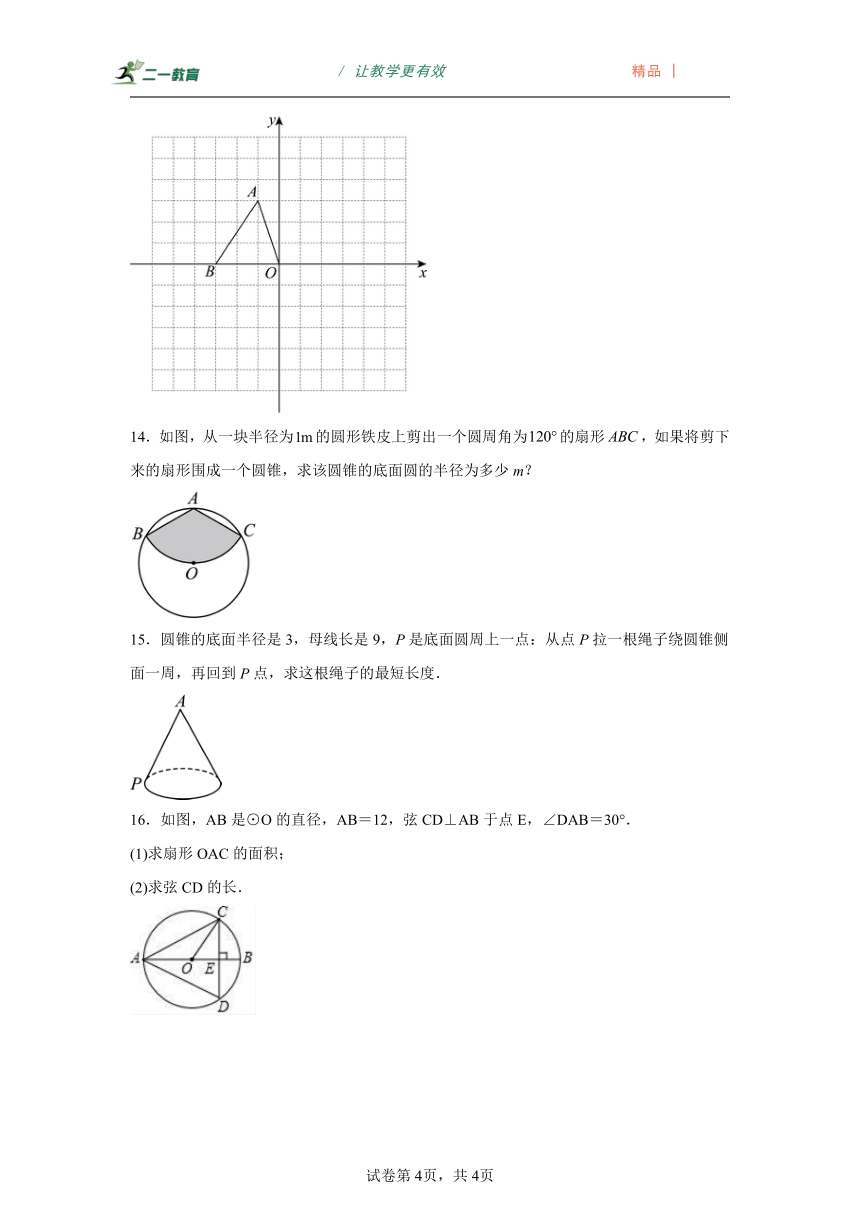
14.如图,从一块半径为的圆形铁皮上剪出一个圆周角为的扇形,如果将剪下来的扇形围成一个圆锥,求该圆锥的底面圆的半径为多少m?
15.圆锥的底面半径是3,母线长是9,P是底面圆周上一点:从点P拉一根绳子绕圆锥侧面一周,再回到P点,求这根绳子的最短长度.
16.如图,AB是⊙O的直径,AB=12,弦CD⊥AB于点E,∠DAB=30°.
(1)求扇形OAC的面积;
(2)求弦CD的长.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】本题考查圆锥的侧面展开图、扇形面积公式,根据圆锥的侧面展开图是扇形,结合扇形面积公式求解即可.
【详解】解:∵圆锥的底面直径为,母线长为,
∴圆锥的侧面积是,
故选:C.
2.C
【分析】本题考查了求圆锥侧面展开图的圆心角,熟练掌握弧长公式是解题关键.
【详解】解:设圆锥的侧面展开图的圆心角度数为,
根据题意有:,
解得:,
故选:C
3.B
【分析】根据圆锥底面圆的周长等于它侧面展开图扇形的弧长,所以只要求出圆锥底面圆的周长即可.此题主要考查了圆锥侧面展开图与圆锥各部分对应情况,这个问题在中考中是重点题型.
【详解】解:圆锥底面圆的半径为3,
圆锥底面圆的周长为:,
圆锥侧面展开图扇形的弧长为:.
故选:B.
4.B
【分析】本题考查了三角形内角和定理,弧长公式;三个阴影扇形的弧长之和可以看作是圆心角为,半径是的弧长,即可求解;掌握弧长公式:,能将所求弧长之和转化为圆心角为,半径都是的弧长是解题的关键.
【详解】解:,
且,,两两不相交,且半径都是,
三个阴影扇形的弧长之和可以看作是圆心角为,
半径是的弧长,
三个阴影扇形的弧长之和为:
,
故选:B.
5.A
【分析】本题主要考查勾股定理,扇形面积计算以及梯形面积计算,连接,由勾股定理求出,然后用求扇形面积公式即可求解,熟练掌握扇形面积计算以及勾股定理是解决本题的关键.
【详解】连接,
在中,,
∴,
,
故选:.
6.A
【分析】本题考查了扇形面积的计算,连接,,根据,是以为直径的半圆的三等分点,可得,是等边三角形,将阴影部分的面积转化为扇形的面积,根据求解即可.
【详解】解:连接,,,
,是以为直径的半圆的三等分点,
,,
又,
、是等边三角形,
,
,
,
弧的长为,
,
解得:,
.
故选:A.
7.A
【分析】本题考查了等边三角形的性质,扇形面积公式,由是等边三角形,得,,过作于点,然后由勾股定理得,求出,,然后代入求值即可,熟练掌握等边三角形的性质和扇形面积公式是解题的关键.
【详解】解:∵是等边三角形,
∴,,
设,
如图,过作于点,
∴,,,
∴由勾股定理得:,
∴,即,
则,
∴,
故选:.
8.B
【分析】先求出正五边形的内角的度数,根据扇形的弧长等于圆锥的底面周长,可求出底面半径.
【详解】解:五边形是正五边形,
,
则弧的长为,即圆锥底面周长为,
设圆锥底面半径为r,则,
∴,
圆锥底面半径为,
故选:B.
【点睛】本题考查正多边形与圆,扇形弧长及圆锥底面半径,掌握扇形弧长、圆周长的计算方法是正确解决问题的关键.
9.
【分析】本题考查了弧长的计算,熟练掌握弧长计算公式是解答本题的关键.弧长计算公式:,其中r为圆的半径,n为圆心角的度数,l为弧长.根据弧长计算公式计算即得答案.
【详解】
该扇形的弧长为.
故答案为:.
10.5
【分析】本题考查利用扇形面积公式求不规则图形面积,根据圆心角都是直角,则绕O顺时针旋转后与重合,由阴影部分面积等于大扇形面积减去小扇形面积,即可得到答案;
【详解】解:由题意可得,如图所示,
,
∵扇形与扇形的圆心角都是,
∴绕点O顺时针旋转后与重合,
∴,
∴,
解得,
故答案为:5.
11.
【分析】记BC中点为点O,连接OD,CD,先证得OD⊥BC,再根据阴影部分的面积计算即可.
【详解】解:记BC中点为点O,连接OD,CD,
∵BC是半圆的直径,
∴O是半圆的圆心,CD⊥AB,
∵△ACB是等腰直角三角形,
∴D是AB中点.
∴OD∥AC,
∴OD⊥BC,
∴阴影部分的面积,
,
,
故答案为:.
【点睛】本题考查了等腰直角三角形的性质,圆周角定理,扇形的面积计算等知识,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键.
12.
【分析】本题主要考查了扇形面积公式,等边三角形的判定和性质,等腰三角形的性质,熟练掌握扇形面积的计算是解题的关键.根据题意求出的长,当三点共线时,取最小值,求出,根据阴影部分的面积即可得到答案.
【详解】解:当三点共线时,取最小值,
是等边三角形,
阴影部分的面积.
故答案为:.
13.(1)如图所示,△A1B1O即为所求;见解析;(2)线段AO旋转时扫过的面积为.
【分析】(1)根据题意,画出图形即可;
(2)先根据勾股定理求出AO,再根据扇形的面积公式计算即可.
【详解】解:(1)根据题意,将△OAB绕点O顺时针旋转90°,如图所示,△A1B1O即为所求;
(2)根据勾股定理:
线段AO旋转时扫过的面积为:=.
【点睛】此题考查的是图形的旋转和求线段旋转时扫过的面积,掌握图形旋转的性质和扇形的面积公式是解决此题的关键.
14.
【分析】本题考查圆锥的有关计算,弧长公式,明确扇形的弧长相当于围成圆锥的底面周长是解决问题的关键.
根据弧长公式求出阴影扇形的弧长,进而可求出围成圆锥的底面半径.
【详解】解:扇形的长为:,
∵扇形的弧长相当于围成圆锥的底面周长,
设围成圆锥的底面半径为,
∴
解得:,
答:围成圆锥的底面半径为.
15.
【分析】本题主要考查圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对直径,转化为求直径的长的问题.
【详解】解:将圆锥侧面沿剪开展平,连接,则就是所求绳子长.
由得,
作,则,,
∴,
∴,,
∴.
16.(1)12π;(2).
【分析】(1)根据垂径定理得到,根据圆周角定理求出∠CAB,根据三角形内角和定理求出∠AOC,根据扇形面积公式计算;(2)根据正弦的定义求出CE,根据垂径定理计算即可.
【详解】(1)∵弦CD⊥AB,
∴,
∴∠CAB=∠DAB=30°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠AOC=120°,
∴扇形OAC的面积==12π;
(2)由圆周角定理得,∠COE=2∠CAB=60°,
∴CE=OC×sin∠COE=3,
∵弦CD⊥AB,
∴CD=2CE=6.
【点睛】本题考查了扇形面积计算,圆周角定理,垂径定理的应用,掌握扇形面积公式是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知圆锥的底面直径为,母线长为,则圆锥的侧面积是( )
A. B. C. D.
2.圆锥的底面圆的半径为1,母线长为3,则它的侧面展开图的圆心角度数为( )
A. B. C. D.
3.如图,已知圆锥的底面圆的半径为3,则这个圆锥的侧面展开图(扇形)的弧长为( )
A. B. C. D.
4.如图,,,两两不相交,且半径都是.则图中三个阴影扇形的弧长之和为( )
A. B. C. D.
5.如图,扇形圆心角为直角,,点在上,以,为邻边构造、边交于点,若,则图中阴影部分的面积为( )
A. B. C. D.
6.如图,已知点,是以为直径的半圆的三等分点,的长为,则图中阴影部分的面积为( )
A. B. C. D.
7.“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若图中阴影部分的面积为,空白部分的面积为,则的值为( )
A. B. C. D.
8.如图,从一个边长是10的正五边形纸片上剪出一个扇形(阴影部分),将剪下来的扇形围成一个圆锥,这个圆锥的底面半径为( )
A.1 B.3 C. D.2
二、填空题
9.一扇形的半径为,圆心角为,则该扇形的弧长为 cm.
10.如图,扇形与扇形的圆心角都是,连接,如果图中阴影部分的面积为,,那么 .
11.如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,以BC为直径作半圆,交AB于点D,则阴影部分的面积是 .
12.如图,扇形的圆心角,半径,点P为扇形内一点,且,延长交于点C,当取最小值时,则图中阴影部分的面积为 .
三、解答题
13.如图,已知△ABO中A(﹣1,3),B(﹣4,0).
(1)画出△ABO绕着原点O按顺时针方向旋转90°后的图形,记为△A1B1O;
(2)求第(1)问中线段AO旋转时扫过的面积.
14.如图,从一块半径为的圆形铁皮上剪出一个圆周角为的扇形,如果将剪下来的扇形围成一个圆锥,求该圆锥的底面圆的半径为多少m?
15.圆锥的底面半径是3,母线长是9,P是底面圆周上一点:从点P拉一根绳子绕圆锥侧面一周,再回到P点,求这根绳子的最短长度.
16.如图,AB是⊙O的直径,AB=12,弦CD⊥AB于点E,∠DAB=30°.
(1)求扇形OAC的面积;
(2)求弦CD的长.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】本题考查圆锥的侧面展开图、扇形面积公式,根据圆锥的侧面展开图是扇形,结合扇形面积公式求解即可.
【详解】解:∵圆锥的底面直径为,母线长为,
∴圆锥的侧面积是,
故选:C.
2.C
【分析】本题考查了求圆锥侧面展开图的圆心角,熟练掌握弧长公式是解题关键.
【详解】解:设圆锥的侧面展开图的圆心角度数为,
根据题意有:,
解得:,
故选:C
3.B
【分析】根据圆锥底面圆的周长等于它侧面展开图扇形的弧长,所以只要求出圆锥底面圆的周长即可.此题主要考查了圆锥侧面展开图与圆锥各部分对应情况,这个问题在中考中是重点题型.
【详解】解:圆锥底面圆的半径为3,
圆锥底面圆的周长为:,
圆锥侧面展开图扇形的弧长为:.
故选:B.
4.B
【分析】本题考查了三角形内角和定理,弧长公式;三个阴影扇形的弧长之和可以看作是圆心角为,半径是的弧长,即可求解;掌握弧长公式:,能将所求弧长之和转化为圆心角为,半径都是的弧长是解题的关键.
【详解】解:,
且,,两两不相交,且半径都是,
三个阴影扇形的弧长之和可以看作是圆心角为,
半径是的弧长,
三个阴影扇形的弧长之和为:
,
故选:B.
5.A
【分析】本题主要考查勾股定理,扇形面积计算以及梯形面积计算,连接,由勾股定理求出,然后用求扇形面积公式即可求解,熟练掌握扇形面积计算以及勾股定理是解决本题的关键.
【详解】连接,
在中,,
∴,
,
故选:.
6.A
【分析】本题考查了扇形面积的计算,连接,,根据,是以为直径的半圆的三等分点,可得,是等边三角形,将阴影部分的面积转化为扇形的面积,根据求解即可.
【详解】解:连接,,,
,是以为直径的半圆的三等分点,
,,
又,
、是等边三角形,
,
,
,
弧的长为,
,
解得:,
.
故选:A.
7.A
【分析】本题考查了等边三角形的性质,扇形面积公式,由是等边三角形,得,,过作于点,然后由勾股定理得,求出,,然后代入求值即可,熟练掌握等边三角形的性质和扇形面积公式是解题的关键.
【详解】解:∵是等边三角形,
∴,,
设,
如图,过作于点,
∴,,,
∴由勾股定理得:,
∴,即,
则,
∴,
故选:.
8.B
【分析】先求出正五边形的内角的度数,根据扇形的弧长等于圆锥的底面周长,可求出底面半径.
【详解】解:五边形是正五边形,
,
则弧的长为,即圆锥底面周长为,
设圆锥底面半径为r,则,
∴,
圆锥底面半径为,
故选:B.
【点睛】本题考查正多边形与圆,扇形弧长及圆锥底面半径,掌握扇形弧长、圆周长的计算方法是正确解决问题的关键.
9.
【分析】本题考查了弧长的计算,熟练掌握弧长计算公式是解答本题的关键.弧长计算公式:,其中r为圆的半径,n为圆心角的度数,l为弧长.根据弧长计算公式计算即得答案.
【详解】
该扇形的弧长为.
故答案为:.
10.5
【分析】本题考查利用扇形面积公式求不规则图形面积,根据圆心角都是直角,则绕O顺时针旋转后与重合,由阴影部分面积等于大扇形面积减去小扇形面积,即可得到答案;
【详解】解:由题意可得,如图所示,
,
∵扇形与扇形的圆心角都是,
∴绕点O顺时针旋转后与重合,
∴,
∴,
解得,
故答案为:5.
11.
【分析】记BC中点为点O,连接OD,CD,先证得OD⊥BC,再根据阴影部分的面积计算即可.
【详解】解:记BC中点为点O,连接OD,CD,
∵BC是半圆的直径,
∴O是半圆的圆心,CD⊥AB,
∵△ACB是等腰直角三角形,
∴D是AB中点.
∴OD∥AC,
∴OD⊥BC,
∴阴影部分的面积,
,
,
故答案为:.
【点睛】本题考查了等腰直角三角形的性质,圆周角定理,扇形的面积计算等知识,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键.
12.
【分析】本题主要考查了扇形面积公式,等边三角形的判定和性质,等腰三角形的性质,熟练掌握扇形面积的计算是解题的关键.根据题意求出的长,当三点共线时,取最小值,求出,根据阴影部分的面积即可得到答案.
【详解】解:当三点共线时,取最小值,
是等边三角形,
阴影部分的面积.
故答案为:.
13.(1)如图所示,△A1B1O即为所求;见解析;(2)线段AO旋转时扫过的面积为.
【分析】(1)根据题意,画出图形即可;
(2)先根据勾股定理求出AO,再根据扇形的面积公式计算即可.
【详解】解:(1)根据题意,将△OAB绕点O顺时针旋转90°,如图所示,△A1B1O即为所求;
(2)根据勾股定理:
线段AO旋转时扫过的面积为:=.
【点睛】此题考查的是图形的旋转和求线段旋转时扫过的面积,掌握图形旋转的性质和扇形的面积公式是解决此题的关键.
14.
【分析】本题考查圆锥的有关计算,弧长公式,明确扇形的弧长相当于围成圆锥的底面周长是解决问题的关键.
根据弧长公式求出阴影扇形的弧长,进而可求出围成圆锥的底面半径.
【详解】解:扇形的长为:,
∵扇形的弧长相当于围成圆锥的底面周长,
设围成圆锥的底面半径为,
∴
解得:,
答:围成圆锥的底面半径为.
15.
【分析】本题主要考查圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对直径,转化为求直径的长的问题.
【详解】解:将圆锥侧面沿剪开展平,连接,则就是所求绳子长.
由得,
作,则,,
∴,
∴,,
∴.
16.(1)12π;(2).
【分析】(1)根据垂径定理得到,根据圆周角定理求出∠CAB,根据三角形内角和定理求出∠AOC,根据扇形面积公式计算;(2)根据正弦的定义求出CE,根据垂径定理计算即可.
【详解】(1)∵弦CD⊥AB,
∴,
∴∠CAB=∠DAB=30°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠AOC=120°,
∴扇形OAC的面积==12π;
(2)由圆周角定理得,∠COE=2∠CAB=60°,
∴CE=OC×sin∠COE=3,
∵弦CD⊥AB,
∴CD=2CE=6.
【点睛】本题考查了扇形面积计算,圆周角定理,垂径定理的应用,掌握扇形面积公式是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
