第十二章全等三角形单元测试卷(含解析)
图片预览



文档简介
第十二章 全等三角形 单元测试卷
一、单选题
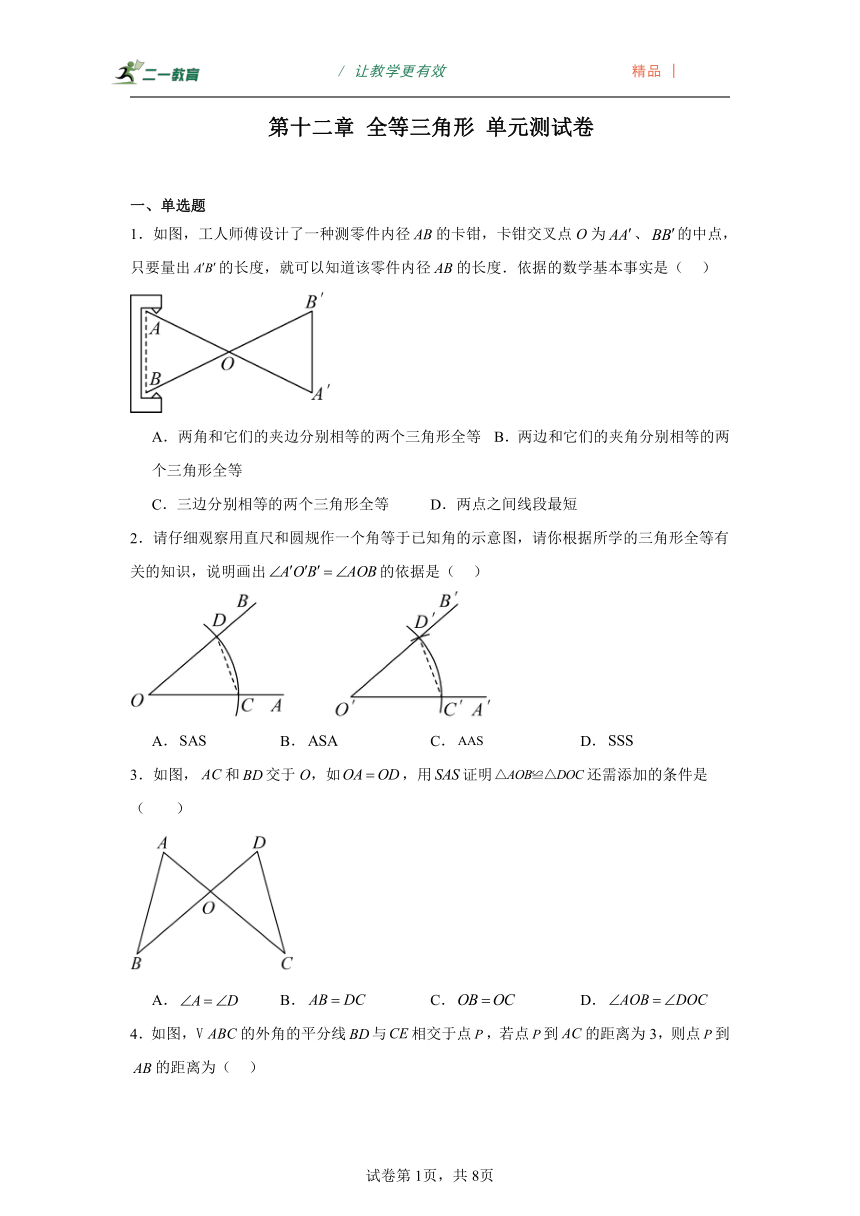
1.如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以知道该零件内径的长度.依据的数学基本事实是( )
A.两角和它们的夹边分别相等的两个三角形全等 B.两边和它们的夹角分别相等的两个三角形全等
C.三边分别相等的两个三角形全等 D.两点之间线段最短
2.请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出的依据是( )
A. B. C. D.
3.如图,和交于O,如,用证明还需添加的条件是( )
A. B. C. D.
4.如图,的外角的平分线与相交于点,若点到的距离为3,则点到的距离为( )
A.1 B.2 C.3 D.4
5.如图,将两根钢条的中点O连在一起,使可绕点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
6.如图,点为定角的平分线上的一个定点,且与互补,若在绕点旋转的过程中,其两边分别与交于点,则一下结论:①恒成立;②的值不变;③四边形的面积不变;④的长不变;其中正确的个数为( )个
A.1 B.2 C.3 D.4
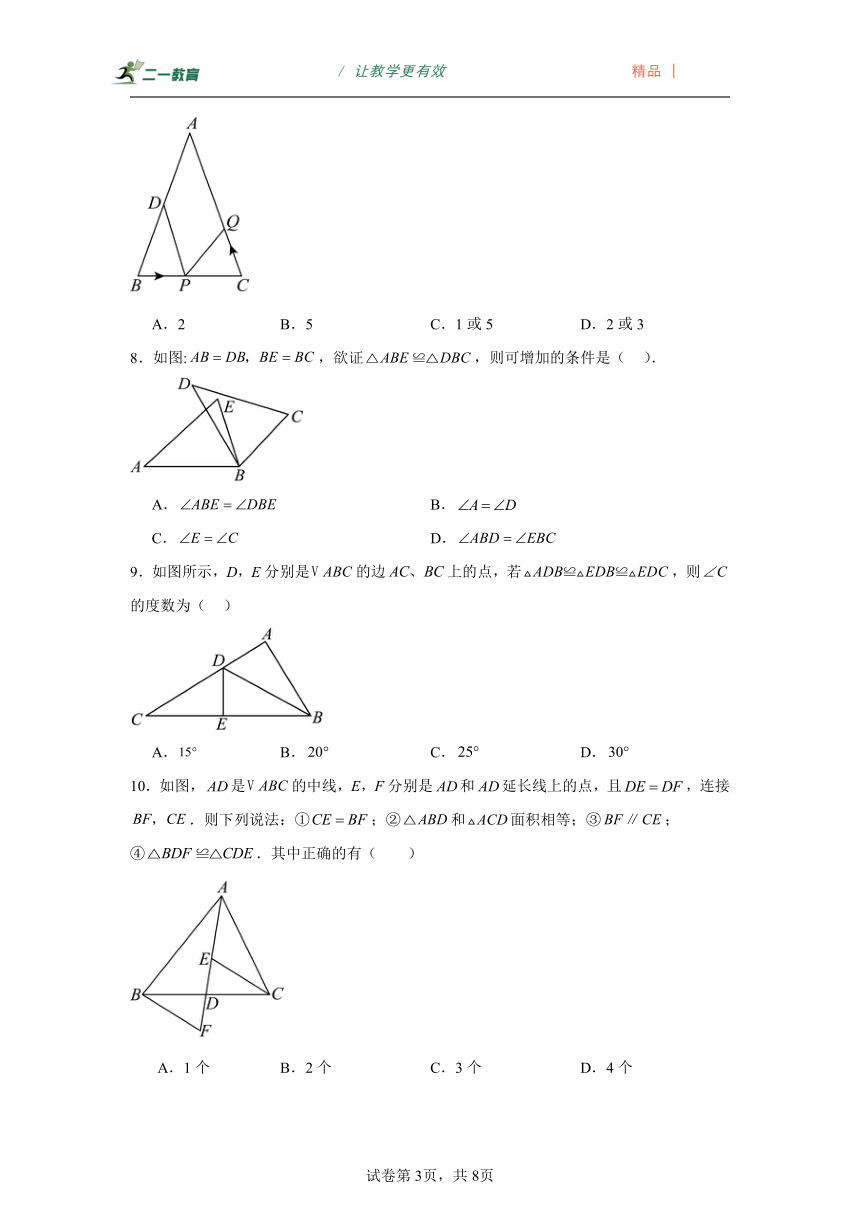
7.中,厘米,厘米,点D为的中点.如果点P在线段上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当与全等时,v的值为( )
A.2 B.5 C.1或5 D.2或3
8.如图:,欲证,则可增加的条件是( ).
A. B.
C. D.
9.如图所示,D,E分别是的边上的点,若,则的度数为( )
A. B. C. D.
10.如图,是的中线,E,F分别是和延长线上的点,且,连接.则下列说法:①;②和面积相等;③; ④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,小明不小心将书上的一个三角形用墨迹污染了一部分,但他很快就根据所学知识画出了一个和书上完全一样的三角形,那么这两个三角形完全一样的依据可简写为 .
12.如图,已知四边形中,厘米,厘米,厘米,,点E为的中点.如果点P在线段上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使与全等.
13.如图,在中,按以下步骤作图:①以点A为圆心,分别交于点M,N,N为圆心,大于,两弧交于点P;③作射线交于点D.若,的面积为2,则的面积为 .
14.如图,在△OAB和△OCD中,,,,连接AC,BD交于点E,BD交OA于点M,AC交OD于点N,连接OE.下列四个结论一定成立的是 (填序号).
①
②
③
④EO平分∠BEC
15.如图,在四边形中,,,,若平分,则四边形的面积为 .
三、解答题
16.如图.在和中,,,.
求证:.
17.把下列证明过程补充完整.
已知:如图,四边形中,.
求证:平分.
证明:∵.
∴在和中,
,
∴( ).
∴∠ =∠ .
∴平分.
18.如图,平分,,,垂足分别为,,点,分别在边,上,且.
(1)求证:;
(2)若,求的度数.
19.如图,在△ABC中,∠ACB = 90°,AC = BC,BE ⊥CE于点E,AD ⊥CE于点D.
(1)求证:△BCE ≌△CAD;
(2)若AD =12, BE =5,求ED的长.
20.两块大小不同的三角板和如图摆放,其中,,,连接.请写出与的关系,并说明理由.
21.如图,在中,平分于点E,点F在上,.求证:.
22.如图,,,点在射线上,且,点在上且,连接,取的中点,连接并延长至,使,连接.
(1)如图1,当点在线段上时.
①用等式表示与的数量关系;
②连接,,直接写出,的数量关系和位置关系;
(2)如图2,当点在线段的延长线上时,依题意补全图形2,猜想②中的结论是否还成立,并证明.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了三角形全等的判定与性质.先根据中点的定义,得出,,再根据对顶角相等得到,从而证得和△全等即可.正确运用三角形全等的判定定理是解题的关键.
【详解】解:点O为、的中点,
,,
由对顶角相等得,
在和中,
,
,
,
即只要量出的长度,就可以知道该零件内径的长度,
故选:B.
2.D
【分析】本题考查了作图基本作图,全等三角形的判定与性质,熟练掌握三角形全等的对应角相等是正确解答本题的关键.
由作法易得,,,依据定理得到≌,由全等三角形的对应角相等得到.
【详解】解:由作法易得,,,
在与中,
,
≌,
全等三角形的对应角相等.
故选:D.
3.C
【分析】此题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解本题的关键.
由,加上对顶角相等,再加上,即可利用得证.
【详解】解:还需添加的添加是,
在和中,
,
∴,
则还需添加的添加是,
故选:C.
4.C
【分析】本题考查了角平分线的性质.过点作于,于,于,然后根据角平分线上的点到角的两边的距离相等可得,从而得解.
【详解】解:如图,过点作于,于,于,
的外角平分线与的外角平分线相交于点,
,,
.
故选:C.
5.A
【分析】本题考查了全等三角形的判定,由已知和图形可得,,,据此即可判断求解,掌握全等三角形的判定方法是解题的关键.
【详解】解:∵点为的中点,
∴,,
又∵,
∴由“边角边”可证明,
故选:.
6.C
【分析】根据角平分线的性质,作,可得,由此可判定①②③,连接,根据三角形三边关系可判定④,由此即可求解.
【详解】解:∵点在的角平分线上,
∴,
如图所示,过点作于点,作于点,
∴,,,
∴在四边形中,,
∵,
∴,即,
∴,
∴,
∴,故①正确;
由①正确可得,,
∴,故②正确;
由可得,
∴,
∴四边形的面积是定值,故③正确;
如图所示,连接,由上述结论可得,,,,,
∴,即的长度发生变化,故④错误;
综上所述,正确的有①②③,共3个,
故选:C .
【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,旋转的性质,四边形面积的计算方法等知识,掌握添加合理的辅助线,构造三角形全等是解题的关键.
7.D
【分析】本题主要考查了全等三角形的判定,此题要分两种情况:①当时,与全等,计算出的长,进而可得运动时间,然后再求v;②当时,,计算出的长,进而可得运动时间,然后再求v.
【详解】解:当时,与全等,
∵点D为的中点,
∴,
∵,
∴,
∵点P在线段上以2厘米/秒的速度由B点向C点运动,
∴运动时间时,
∵,
∴,
∴;
当时,,
∵,
∴,
∵,
∴,
∴运动时间为,
∴.
故v的值为2或3.
故选:.
8.D
【分析】本题考查全等三角形的判定,掌握全等三角形的判定定理是解题的关键.
由结合全等三角形的判定定理,即可找出需添加条件,结合图形利用角的计算即可得出添加可证出.
【详解】解:添加,
∵,
∴.
又∵,
∴.
故选:D.
9.D
【分析】此题考查了全等三角形对应角相等的性质,直角三角形两锐角互余的性质,解题的关键是求出.
根据全等三角形对应角相等,得到,根据,求出,在利用直角三角形两锐角互余求解即可.
【详解】解:∵,
∴,
∵,
∴,
在中,,
∴,
故选D.
10.D
【分析】本题主要考查了全等三角形的判定与性质、等底等高的三角形的面积相等、平行线的判定等知识点,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
根据三角形中线的定义可得,然后利用“”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:∵是的中线,
∴,
在和中,
,
∴,故④正确;
∴,故①正确,
∴,故③正确;
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的是①②③④,共4个.
故选:D.
11./角边角
【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出.
【详解】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“”定理作出完全一样的三角形.
故答案为:
【点睛】本题考查了全等三角形判定的实际运用,熟练掌握判定定理并灵活运用是解题的关键.
12.2或3
【分析】本题考查全等三角形的判定.根据题意,分两种情况:当时,与全等,或时,与全等,分别求解即可.
【详解】解:设点运动时间为秒,则,,
,
当时,与全等,
此时,,
解得,
,
此时,点的运动速度为(厘米/秒),
当时,与全等,
此时,,
解得,
点的运动速度为(厘米/秒).
故答案为:2或3.
13.3
【分析】本题考查了基本作图—作已知角的角平分线,角平分线的性质,利用基本作图得到平分,再根据角平分线的性质得点D到的距离相等,于是利用三角形面积公式得到,从而可计算出的面积.
【详解】解:由作法得:平分,
点D到的距离相等,
,
.
故答案为:3.
14.①②④.
【分析】证明△AOC≌△BOD,即可判断①;利用△AOC≌△BOD,推出∠CAO=∠DBO,得到∠OAB+∠OBA=∠OAB+∠ABE+∠CAO,由三角形内角和定理即可判断②;无法证明△AON≌△BOM,即无法判断,由此判断③;过O作OG⊥BD于G,OH⊥AC于H,根据全等三角形的性质得到OG=OH,由此判断④
【详解】解:在△OAB和△OCD中,,
∴∠AOC=∠BOD,
∵,,
∴△AOC≌△BOD,
∴AC=BD,故①正确;
∵△AOC≌△BOD,
∴∠CAO=∠DBO,
∴∠OAB+∠OBA=∠OAB+∠ABE+∠CAO,
∵∠OAB+∠OBA+∠AOB=180°,∠OAB+∠ABE+∠CAO+∠AEB=180°,
∴,故②正确;
∵OA=OB,∠NAO=∠MBO,无法证明∠BOM=∠AON,
∴无法证明△AON≌△BOM,即无法判断,故③错误;
过O作OG⊥BD于G,OH⊥AC于H,
∵△AOC≌△BOD,AC=BD,
∴,
∴OG=OH,
∴EO平分∠BEC,故④正确;
故答案为:①②④.
【点睛】此题考查了全等三角形的判定及性质,角平分线的判定定理,正确掌握全等三角形的判定定理是解题的关键.
15.20
【分析】本题主要考查了角平分线的性质定理,理解并掌握角平分线的性质定理是解题关键.过点作,交延长线于点,根据“角平分线上的点到角的两边的距离相等”可得,然后由四边形的面积求解,即可获得答案.
【详解】解:如下图,过点作,交延长线于点,
∵平分,,,
∴,
∴四边形的面积
.
故答案为:20.
16.证明见解析
【分析】先根据角的和差可得,再根据三角形全等的判定定理与性质即可得证.
【详解】证明:,
,即,
在和中,
【点睛】本题考查了三角形全等的判定定理与性质,熟练掌握三角形全等的判定方法是解题关键.
17.,,,
【分析】此题重点考查全等三角形的判定与性质.根据证明,得,于是得到问题的答案.
【详解】证明:∵.
∴在和中,
,
∴.
∴.
∴平分.
故答案为:,,,.
18.(1)见解析
(2)
【分析】本题主要考查了垂线定义,全等三角形的判定及性质,角平分线的性质定理,熟练掌握全等三角形的判定及性质及角平分线的性质定理是解题的关键。
()证明(),即可得证;
()根据四边形的内角和及垂线定义得再根据即可得解.
【详解】(1)证明:∵平分,,,
∴(角平分线上的点到角两边的距离相等),
在和中,
,
∴(),
∴(全等三角形的对应角相等);
(2)解:∵,,
∴
∵四边形的内角和,
∴,
∵,
∴,
∵,
∴.
19.(1)见解析;(2)ED的长为7.
【分析】(1)根据AAS证明三角形全等即可;
(2)根据全等三角形的性质得到AD=CE=12,CD=BE=5,从而求得ED的长.
【详解】解:(1)证明:∵BE ⊥CE于点E,AD ⊥CE于点D,
∴∠CEB=∠ADC=90°,
∴∠ACD+∠CAD=90°,
∵∠ACB = 90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
又∵AC = BC,
∴≌;
(2)由(1)知,≌,
∴BE=CD,CE=AD,
∵AD =12, BE =5,
∴CE=12,CD=5,
∴ED=CE-CD=12-5=7.
【点睛】本题考查了全等三角形的判定与性质,熟练掌握判定及性质定理是解题的关键.
20.,,理由见解析
【分析】本题考查了三角形全等的判定与性质,设延长线交于点O,交于点H,根据条件证即可求解.
【详解】解:,,理由如下:
如图,设延长线交于点O,交于点H,
∵
在与中,
.
,
.
21.见解析
【分析】本题考查全等三角形的判定与性质、角平分线的性质,根据角平分线的性质和全等三角形的判定方法可以证明和全等,从而可以证明结论成立.
【详解】证明:∵平分,,
∴,
在和中,
,
∴,
∴.
22.(1)①;②,,理由见详解
(2)补全图形见详解,②的结论还成立,证明见详解
【分析】(1)①证明,得出,则可得出结论;
②连接,,证明,得出,,则可得出结论;
(2)根据题意补全图形,证明,得出,,则可得出结论.
【详解】(1)解:(1)①,
为的中点,
,
,,
,
,
,
;
②,,
理由:连接,,
,
,
,
,
设,则,
,
,
,
,
,
,
,,
,
,,
,
,
;
(2)补全图形如下,②的结论还成立,
证明:连接,,
同①可证,,
设,则,
,,
,
,而,,
,
,,
,
.
【点睛】本题是三角形综合题,考查了全等三角形的判定与性质、等腰直角三角形的性质、平行线的性质、直角三角形的性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,工人师傅设计了一种测零件内径的卡钳,卡钳交叉点O为、的中点,只要量出的长度,就可以知道该零件内径的长度.依据的数学基本事实是( )
A.两角和它们的夹边分别相等的两个三角形全等 B.两边和它们的夹角分别相等的两个三角形全等
C.三边分别相等的两个三角形全等 D.两点之间线段最短
2.请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出的依据是( )
A. B. C. D.
3.如图,和交于O,如,用证明还需添加的条件是( )
A. B. C. D.
4.如图,的外角的平分线与相交于点,若点到的距离为3,则点到的距离为( )
A.1 B.2 C.3 D.4
5.如图,将两根钢条的中点O连在一起,使可绕点自由转动,就做成了一个测量工件,则的长等于内槽宽,那么判定的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
6.如图,点为定角的平分线上的一个定点,且与互补,若在绕点旋转的过程中,其两边分别与交于点,则一下结论:①恒成立;②的值不变;③四边形的面积不变;④的长不变;其中正确的个数为( )个
A.1 B.2 C.3 D.4
7.中,厘米,厘米,点D为的中点.如果点P在线段上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当与全等时,v的值为( )
A.2 B.5 C.1或5 D.2或3
8.如图:,欲证,则可增加的条件是( ).
A. B.
C. D.
9.如图所示,D,E分别是的边上的点,若,则的度数为( )
A. B. C. D.
10.如图,是的中线,E,F分别是和延长线上的点,且,连接.则下列说法:①;②和面积相等;③; ④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,小明不小心将书上的一个三角形用墨迹污染了一部分,但他很快就根据所学知识画出了一个和书上完全一样的三角形,那么这两个三角形完全一样的依据可简写为 .
12.如图,已知四边形中,厘米,厘米,厘米,,点E为的中点.如果点P在线段上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使与全等.
13.如图,在中,按以下步骤作图:①以点A为圆心,分别交于点M,N,N为圆心,大于,两弧交于点P;③作射线交于点D.若,的面积为2,则的面积为 .
14.如图,在△OAB和△OCD中,,,,连接AC,BD交于点E,BD交OA于点M,AC交OD于点N,连接OE.下列四个结论一定成立的是 (填序号).
①
②
③
④EO平分∠BEC
15.如图,在四边形中,,,,若平分,则四边形的面积为 .
三、解答题
16.如图.在和中,,,.
求证:.
17.把下列证明过程补充完整.
已知:如图,四边形中,.
求证:平分.
证明:∵.
∴在和中,
,
∴( ).
∴∠ =∠ .
∴平分.
18.如图,平分,,,垂足分别为,,点,分别在边,上,且.
(1)求证:;
(2)若,求的度数.
19.如图,在△ABC中,∠ACB = 90°,AC = BC,BE ⊥CE于点E,AD ⊥CE于点D.
(1)求证:△BCE ≌△CAD;
(2)若AD =12, BE =5,求ED的长.
20.两块大小不同的三角板和如图摆放,其中,,,连接.请写出与的关系,并说明理由.
21.如图,在中,平分于点E,点F在上,.求证:.
22.如图,,,点在射线上,且,点在上且,连接,取的中点,连接并延长至,使,连接.
(1)如图1,当点在线段上时.
①用等式表示与的数量关系;
②连接,,直接写出,的数量关系和位置关系;
(2)如图2,当点在线段的延长线上时,依题意补全图形2,猜想②中的结论是否还成立,并证明.
/ 让教学更有效 精品 |
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了三角形全等的判定与性质.先根据中点的定义,得出,,再根据对顶角相等得到,从而证得和△全等即可.正确运用三角形全等的判定定理是解题的关键.
【详解】解:点O为、的中点,
,,
由对顶角相等得,
在和中,
,
,
,
即只要量出的长度,就可以知道该零件内径的长度,
故选:B.
2.D
【分析】本题考查了作图基本作图,全等三角形的判定与性质,熟练掌握三角形全等的对应角相等是正确解答本题的关键.
由作法易得,,,依据定理得到≌,由全等三角形的对应角相等得到.
【详解】解:由作法易得,,,
在与中,
,
≌,
全等三角形的对应角相等.
故选:D.
3.C
【分析】此题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解本题的关键.
由,加上对顶角相等,再加上,即可利用得证.
【详解】解:还需添加的添加是,
在和中,
,
∴,
则还需添加的添加是,
故选:C.
4.C
【分析】本题考查了角平分线的性质.过点作于,于,于,然后根据角平分线上的点到角的两边的距离相等可得,从而得解.
【详解】解:如图,过点作于,于,于,
的外角平分线与的外角平分线相交于点,
,,
.
故选:C.
5.A
【分析】本题考查了全等三角形的判定,由已知和图形可得,,,据此即可判断求解,掌握全等三角形的判定方法是解题的关键.
【详解】解:∵点为的中点,
∴,,
又∵,
∴由“边角边”可证明,
故选:.
6.C
【分析】根据角平分线的性质,作,可得,由此可判定①②③,连接,根据三角形三边关系可判定④,由此即可求解.
【详解】解:∵点在的角平分线上,
∴,
如图所示,过点作于点,作于点,
∴,,,
∴在四边形中,,
∵,
∴,即,
∴,
∴,
∴,故①正确;
由①正确可得,,
∴,故②正确;
由可得,
∴,
∴四边形的面积是定值,故③正确;
如图所示,连接,由上述结论可得,,,,,
∴,即的长度发生变化,故④错误;
综上所述,正确的有①②③,共3个,
故选:C .
【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,旋转的性质,四边形面积的计算方法等知识,掌握添加合理的辅助线,构造三角形全等是解题的关键.
7.D
【分析】本题主要考查了全等三角形的判定,此题要分两种情况:①当时,与全等,计算出的长,进而可得运动时间,然后再求v;②当时,,计算出的长,进而可得运动时间,然后再求v.
【详解】解:当时,与全等,
∵点D为的中点,
∴,
∵,
∴,
∵点P在线段上以2厘米/秒的速度由B点向C点运动,
∴运动时间时,
∵,
∴,
∴;
当时,,
∵,
∴,
∵,
∴,
∴运动时间为,
∴.
故v的值为2或3.
故选:.
8.D
【分析】本题考查全等三角形的判定,掌握全等三角形的判定定理是解题的关键.
由结合全等三角形的判定定理,即可找出需添加条件,结合图形利用角的计算即可得出添加可证出.
【详解】解:添加,
∵,
∴.
又∵,
∴.
故选:D.
9.D
【分析】此题考查了全等三角形对应角相等的性质,直角三角形两锐角互余的性质,解题的关键是求出.
根据全等三角形对应角相等,得到,根据,求出,在利用直角三角形两锐角互余求解即可.
【详解】解:∵,
∴,
∵,
∴,
在中,,
∴,
故选D.
10.D
【分析】本题主要考查了全等三角形的判定与性质、等底等高的三角形的面积相等、平行线的判定等知识点,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
根据三角形中线的定义可得,然后利用“”证明和全等,根据全等三角形对应边相等可得,全等三角形对应角相等可得,再根据内错角相等,两直线平行可得,最后根据等底等高的三角形的面积相等判断出②正确.
【详解】解:∵是的中线,
∴,
在和中,
,
∴,故④正确;
∴,故①正确,
∴,故③正确;
∵,点A到的距离相等,
∴和面积相等,故②正确,
综上所述,正确的是①②③④,共4个.
故选:D.
11./角边角
【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出.
【详解】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“”定理作出完全一样的三角形.
故答案为:
【点睛】本题考查了全等三角形判定的实际运用,熟练掌握判定定理并灵活运用是解题的关键.
12.2或3
【分析】本题考查全等三角形的判定.根据题意,分两种情况:当时,与全等,或时,与全等,分别求解即可.
【详解】解:设点运动时间为秒,则,,
,
当时,与全等,
此时,,
解得,
,
此时,点的运动速度为(厘米/秒),
当时,与全等,
此时,,
解得,
点的运动速度为(厘米/秒).
故答案为:2或3.
13.3
【分析】本题考查了基本作图—作已知角的角平分线,角平分线的性质,利用基本作图得到平分,再根据角平分线的性质得点D到的距离相等,于是利用三角形面积公式得到,从而可计算出的面积.
【详解】解:由作法得:平分,
点D到的距离相等,
,
.
故答案为:3.
14.①②④.
【分析】证明△AOC≌△BOD,即可判断①;利用△AOC≌△BOD,推出∠CAO=∠DBO,得到∠OAB+∠OBA=∠OAB+∠ABE+∠CAO,由三角形内角和定理即可判断②;无法证明△AON≌△BOM,即无法判断,由此判断③;过O作OG⊥BD于G,OH⊥AC于H,根据全等三角形的性质得到OG=OH,由此判断④
【详解】解:在△OAB和△OCD中,,
∴∠AOC=∠BOD,
∵,,
∴△AOC≌△BOD,
∴AC=BD,故①正确;
∵△AOC≌△BOD,
∴∠CAO=∠DBO,
∴∠OAB+∠OBA=∠OAB+∠ABE+∠CAO,
∵∠OAB+∠OBA+∠AOB=180°,∠OAB+∠ABE+∠CAO+∠AEB=180°,
∴,故②正确;
∵OA=OB,∠NAO=∠MBO,无法证明∠BOM=∠AON,
∴无法证明△AON≌△BOM,即无法判断,故③错误;
过O作OG⊥BD于G,OH⊥AC于H,
∵△AOC≌△BOD,AC=BD,
∴,
∴OG=OH,
∴EO平分∠BEC,故④正确;
故答案为:①②④.
【点睛】此题考查了全等三角形的判定及性质,角平分线的判定定理,正确掌握全等三角形的判定定理是解题的关键.
15.20
【分析】本题主要考查了角平分线的性质定理,理解并掌握角平分线的性质定理是解题关键.过点作,交延长线于点,根据“角平分线上的点到角的两边的距离相等”可得,然后由四边形的面积求解,即可获得答案.
【详解】解:如下图,过点作,交延长线于点,
∵平分,,,
∴,
∴四边形的面积
.
故答案为:20.
16.证明见解析
【分析】先根据角的和差可得,再根据三角形全等的判定定理与性质即可得证.
【详解】证明:,
,即,
在和中,
【点睛】本题考查了三角形全等的判定定理与性质,熟练掌握三角形全等的判定方法是解题关键.
17.,,,
【分析】此题重点考查全等三角形的判定与性质.根据证明,得,于是得到问题的答案.
【详解】证明:∵.
∴在和中,
,
∴.
∴.
∴平分.
故答案为:,,,.
18.(1)见解析
(2)
【分析】本题主要考查了垂线定义,全等三角形的判定及性质,角平分线的性质定理,熟练掌握全等三角形的判定及性质及角平分线的性质定理是解题的关键。
()证明(),即可得证;
()根据四边形的内角和及垂线定义得再根据即可得解.
【详解】(1)证明:∵平分,,,
∴(角平分线上的点到角两边的距离相等),
在和中,
,
∴(),
∴(全等三角形的对应角相等);
(2)解:∵,,
∴
∵四边形的内角和,
∴,
∵,
∴,
∵,
∴.
19.(1)见解析;(2)ED的长为7.
【分析】(1)根据AAS证明三角形全等即可;
(2)根据全等三角形的性质得到AD=CE=12,CD=BE=5,从而求得ED的长.
【详解】解:(1)证明:∵BE ⊥CE于点E,AD ⊥CE于点D,
∴∠CEB=∠ADC=90°,
∴∠ACD+∠CAD=90°,
∵∠ACB = 90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
又∵AC = BC,
∴≌;
(2)由(1)知,≌,
∴BE=CD,CE=AD,
∵AD =12, BE =5,
∴CE=12,CD=5,
∴ED=CE-CD=12-5=7.
【点睛】本题考查了全等三角形的判定与性质,熟练掌握判定及性质定理是解题的关键.
20.,,理由见解析
【分析】本题考查了三角形全等的判定与性质,设延长线交于点O,交于点H,根据条件证即可求解.
【详解】解:,,理由如下:
如图,设延长线交于点O,交于点H,
∵
在与中,
.
,
.
21.见解析
【分析】本题考查全等三角形的判定与性质、角平分线的性质,根据角平分线的性质和全等三角形的判定方法可以证明和全等,从而可以证明结论成立.
【详解】证明:∵平分,,
∴,
在和中,
,
∴,
∴.
22.(1)①;②,,理由见详解
(2)补全图形见详解,②的结论还成立,证明见详解
【分析】(1)①证明,得出,则可得出结论;
②连接,,证明,得出,,则可得出结论;
(2)根据题意补全图形,证明,得出,,则可得出结论.
【详解】(1)解:(1)①,
为的中点,
,
,,
,
,
,
;
②,,
理由:连接,,
,
,
,
,
设,则,
,
,
,
,
,
,
,,
,
,,
,
,
;
(2)补全图形如下,②的结论还成立,
证明:连接,,
同①可证,,
设,则,
,,
,
,而,,
,
,,
,
.
【点睛】本题是三角形综合题,考查了全等三角形的判定与性质、等腰直角三角形的性质、平行线的性质、直角三角形的性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
