第2章一元二次方程例题精讲与跟踪训练(含解析)
文档属性
| 名称 | 第2章一元二次方程例题精讲与跟踪训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 889.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 07:39:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2章一元二次方程例题精讲与跟踪训练-数学九年级上册北师大版
一、单选题
1.关于的方程是一元二次方程,则□可以是( )
A. B. C. D.
2.关于x的一元二次方程没有实数根,则实数m的取值范围是( )
A. B. C. D.
3.若是一元二次方程的一个解,则方程的另一个解为( )
A. B. C. D.
4.一元二次方程的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
5.探讨关于x的一元二次方程总有实数根的条件,下面三名同学给出建议:甲:a,b同号;乙:;丙:.其中符合条件的是( )
A.甲,乙,丙都正确 B.只有甲不正确
C.甲,乙,丙都不正确 D.只有乙不正确
6.将一元二次方程化成(a,b为常数)的形式,则a,b的值分别是( )
A. B. C.4,21 D.
7.武汉市某区2022年应届初中毕业生为5万人,2023年、2024年两届毕业生一共为12万人,设2022年到2024年平均每年学生人数增长的百分率为x,则方程可列为( )
A. B.
C. D.
8.如图,某摄影爱好者拍摄了一副长为,宽为的杭州金沙湖大剧院风景照,现在风景画四周一条等宽的纸边,制成一幅矩形挂图.若要使整幅挂图的面积是,设纸边的宽为(),则应满足的方程是( )
A. B.
C. D.
二、填空题
9.一元二次方程的解是 .
10.关于x的方程有两个相等的实数根,则k值为 .
11.若a是方程的一个根,则代数式的值为 .
12.已知实数、满足,,则的值为 .
13.有关部门决定降低药价,对某种原价为100元的药品进行连续两次降价后为81元.则平均每次降价的百分率为 .
14.如图,邻边不等的矩形花圃,它的一边利用已有的16m的围墙,另外三边所围的栅栏的总长度是32m,若矩形花圃的面积为,则的长度是 m.
15.等腰三角形的边长是方程的解,则这个三角形的周长是 .
16.对于实数,我们定义符号的意义为:当时,;当时,,如,则方程的解为 .
三、解答题
17.解方程:
(1);
(2).
18.已知关于x的一元二次方程.
(1)证明:无论为何值,方程总有两个不相等的实数根:
(2)若方程的两个实数根分别为,且,求的值.
19.某品牌纪念品每套成本为元,当售价为元时,平均每天的销售量为套,经试销统计发现,如果该品牌纪念品售价每上涨元,那么平均每天的销售量将减少套,为了维护消费者利益,物价部门规定:该品牌纪念品售价不能超过进价的,商家想要使这种纪念品的销售利润平均每天达到元,求每套纪念品应定价多少元?
20.如图,某农场老板准备建造一个矩形养兔场,他打算让矩形养兔场的一边完全靠着墙,墙可利用的长度为24米,另外三面用长度为50米的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分),设矩形垂直于墙的边的长为x 米,矩形的面积记为y平方米.
(1)当时, 米, 平方米;
(2)若要使矩形养兔场的面积为300平方米,则垂直于墙的一边的长为多少米?
21.在矩形中,,一动点从点出发沿着方向以的速度运动,另一动点从点A出发沿着边以的速度运动,两点同时出发,运动时间为.
(1)当为何值时为等腰三角形?
(2)若的面积是矩形面积的,求的值;
(3)的面积能否等于五边形面积的?若能,求出的值;若不能,说明理由;
(4)当时,求证:四边形的面积是一个定值.
22.综合与实践
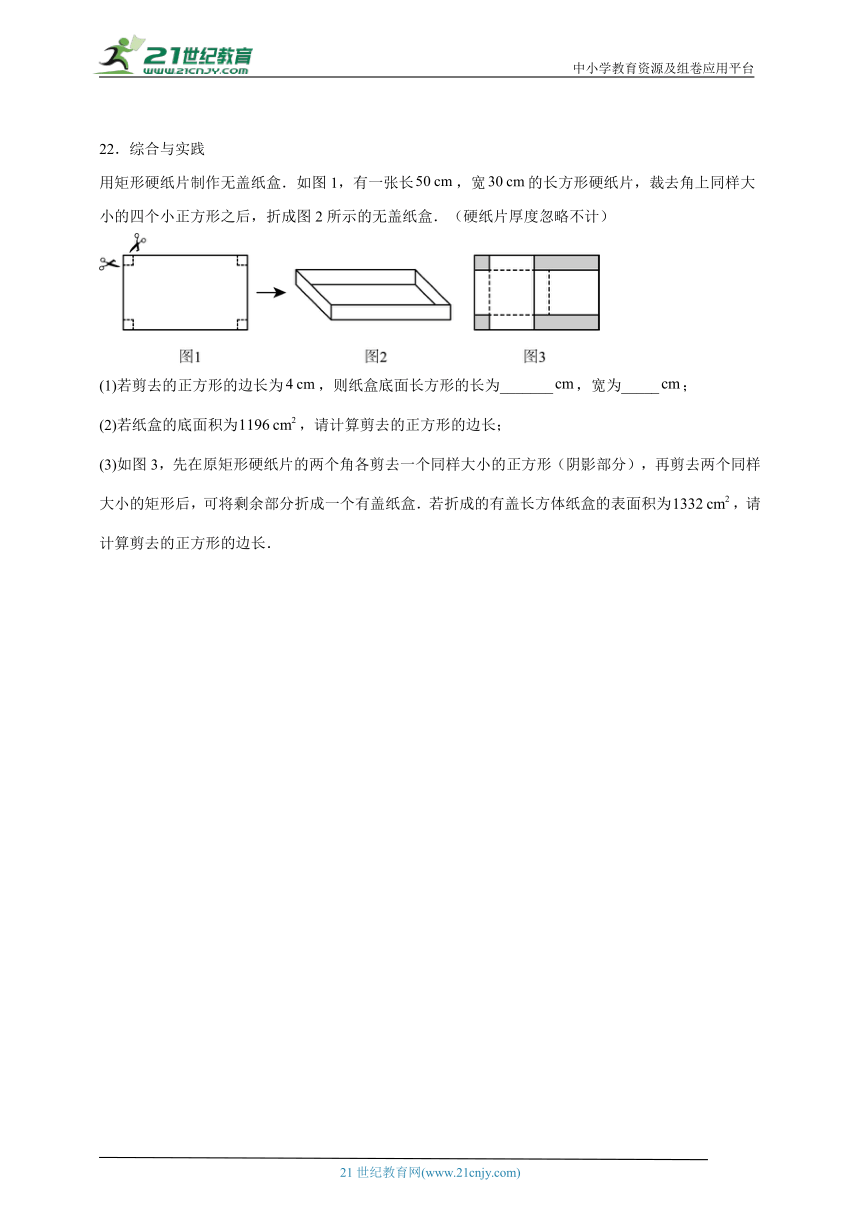
用矩形硬纸片制作无盖纸盒.如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若剪去的正方形的边长为,则纸盒底面长方形的长为_______,宽为_____;
(2)若纸盒的底面积为,请计算剪去的正方形的边长;
(3)如图3,先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 A A A B B A D D
1.A
【分析】本题主要考查一元二次方程的定义,判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.根据一元二次方程的定义判断作答即可.
【详解】解:A.,是一元二次方程,此选项符合题意;
B.,是二元二次方程,此选项不符合题意;
C.,是二元二次方程,此选项不符合题意;
D.,是一元一次方程,此选项不符合题意;
故选:A.
2.A
【分析】本题考查了一元二次方程根的判别式.根据一元二次方程根的判别式小于0,方程没有实数根,列不等式计算即可.
【详解】解:关于x的一元二次方程化为一般式为,
根据题意得:,
即,
解得:,
故选:A.
3.A
【分析】此题主要考查了一元二次方程根与系数的关系,解题的关键是熟练掌握一元二次方程根与系数的关系.根据根与系数的关系即可求解.
【详解】解:设方程的另一个根为,
则,
∴.
故选:A.
4.B
【分析】本题主要考查了根的判别式,一元二次方程,当时,方程有两个不相等的实数根;当时,方程没有实数根;当时,方程有两个相等的实数根.
先求出一元二次方程根的判别式的值,然后判断即可.
【详解】解:∵一元二次方程,
∴,
∴方程有两个不相等的实数根.
故选:B.
5.B
【分析】本题考查一元二次方程有实数根的条件,根据题中所给条件,结合一元二次方程根的判别式讨论是解决问题的关键.
根据一元二次方程根的判别式求解,然后根据各种说法的条件逐项验证即可.
【详解】解:关于x的一元二次方程根的判别式为:,
甲:当a,b同号时,若两数均为负数,就不能确保的符号为正,不符合题意;
乙:当时,得到,从而,总有实数根,符合题意;
丙:当时,得到,从而,总有实数根,符合题意;
综上所述,甲的建议不能满足题意,乙和丙的建议满足题意,
故选:B.
6.A
【分析】本题考查了用配方法解一元二次方程,能正确配方是解此题的关键.将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后即可得出答案.
【详解】解:,
,
则,
即,
,,
故选:A.
7.D
【分析】本题考查了由实际问题抽象出一元二次方程,平均每年学生人数增长的百分率为x,根据2023年、2024年年两届毕业生一共为万人,即可得出关于x 的一元二次方程,此题得解.
【详解】解:平均每年学生人数增长的百分率为x,方程可列为,
故选:D.
8.D
【分析】本题考查了一元二次方程的应用.根据题意正确的列方程是解题的关键.
依题意得,面积为,然后作答即可.
【详解】解:由题意知,矩形挂图的长为,宽为,
依题意得,面积为,
故选:D.
9.
【分析】本题主要考查了解一元二次方程.熟练掌握因式分解法解一元二次方程,是解决问题的关键.
移项,提公因式x,化成两个一元一次方程解答即可.
【详解】∵,
∴移项得,,
分解因式得,,
∴,
∴.
故答案为:.
10.
【分析】本题考查了一元二次方程根的判别式,对于一元二次方程,当时,一元二次方程有两个不相等的实数根;当时,一元二次方程有两个相等的实数根;当时,一元二次方程没有实数根.
【详解】解:∵方程有两个相等的实数根,
∴,即,
解得:,
故答案为:.
11.7
【分析】本题考查了一元二次方程的解、求代数式的值,由题意得出,推出,整体代入计算即可得出答案.
【详解】解:∵a是方程的一个根,
∴,
∴,
∴,
故答案为:.
12.或2
【分析】本题考查一元二次方程根与系数的关系,根据题意可知,实数是一元二次方程的实数根,再根据一元二次方程根与系数的关系及方程相等的两实数根解题即可.
【详解】解:依题意,实数是一元二次方程的实数根,
若,则
;
若,则
故答案为:或2.
13.10%
【分析】本题主要考查求平均变化率的方法、解一元二次方程,若设变化前的量为,变化后的量为,平均变化率为,则经过两次变化后的数量关系为:,解题的关键是熟记公式并应用.
设平均每次降价的百分率为,根据题意和公式即可列出方程,求解即可.
【详解】解:设平均每次降价的百分率为,
由题意得:,
解得:或(舍去),
平均每次降价的百分率为10%.
故答案为:10%.
14.10
【分析】本题考查一元二次方程的应用,设,根据矩形的面积公式,列出一元二次方程,进行求解即可.
【详解】解:设,则:,由题意,得:
,
解得:,
当时,,不符合题意,舍去
当时,,符合题意;
故的长度是;
故答案为:10
15.11或13/13或11
【分析】本题主要考查了等腰三角形的定义,构成三角形的条件,解一元二次方程,先利用因式分解法求出方程的解为或,再分当腰长为3时,当腰长为5时,两种情况根据构成三角形的条件讨论求解即可.
【详解】解:解方程得:或,
当腰长为3时,则等腰三角形的三边长为3,3,5,
∵,
∴此时能构成三角形,
∴这个三角形的周长是;
当腰长为5时,则等腰三角形的三边长为3,5,5,
∵,
∴此时能构成三角形,
∴这个三角形的周长是;
综上所述,这个三角形的周长是11或13,
故答案为:11或13.
16.或3
【分析】本题主要考查了新定义,解一元二次方程,解题的关键是正确理解题目所给新定义的运算法则,以及解一元二次方程的方法和步骤.根据题目所给新定义,列出方程求解即可.
【详解】解:, ,
∴,即,
解得:,
故答案为:或3.
17.(1),
(2)
【分析】本题考查了解一元二次方程,熟练掌握各种解法是解题的关键.
(1)因式分解法求解即可;
(2)公式法求解即可.
【详解】(1)解:,
或,
解得:或,
∴原方程的根为:,;
(2)解:
,
∴,
∴原方程的根为:.
18.(1)证明见解析
(2)
【分析】本题主要考查了一元二次方程根的判别式,根与系数的关系:
(1)只需要证明即可;
(2)根据根与系数的关系得到,,再由已知条件建立方程组求出,据此代值计算即可.
【详解】(1)证明:由题意得,,
∵,
∴,
∴无论为何值,方程总有两个不相等的实数根:
(2)解:∵关于x的一元二次方程的两个实数根分别为,
∴,
又∵,
∴,
解得,
∴,
∴.
19.元
【分析】本题考查了一元二次方程的应用,设每套纪念品应定价为元,根据题意列出方程组,求出的值,再结合售价不能超过进价的进行判断即可求解,根据题意正确列出方程是解题的关键.
【详解】解:设每套纪念品应定价为元,
由题意得,,
解得,,
当时,,符合题意,
当时,,不合题意,
∴,
答:每套纪念品应定价为元.
20.(1)10;200
(2)的长为15米
【分析】本题考查了一元二次方程的实际应用.
(1)根据题意可得,即可求出,根据长方形面积公式,即可求出y;
(2)根据题意可得,则,根据长方形面积公式,列出方程求解即可.
【详解】(1)解:当时,,
,
故答案为:10,200;
(2)解:由题意知:,则,
∴,
整理得:,
解得:,,
当时,,应舍去,
∴的长为15米.
21.(1)
(2)
(3)不能,理由见解析
(4)见解析
【分析】(1)用含t的式子表示,,的长,根据为等腰三角形得到,代入后解方程即可;
(2)表示出和矩形的面积,根据的面积是矩形面积的,即可列出方程,求解即可;
(3)当时,,代入后得到一元二次方程,根据一元二次方程根的判别式即可解答;
(4)表示出和的面积,根据,代入后化简即可得证.
【详解】(1)解:当运动时,,,
∴,
∵在矩形中,
∴当为等腰三角形时,,
∴,
解得;
(2)解:∵,
,
∴当时,,
解得;
(3)解:当时,,
∵,,
∴,
整理,得,
∵,
∴方程没有实数根,
∴的面积不能等于五边形面积的;
(4)证明:∵四边形是矩形,
∴,,
∵当运动时,,,,,
∴,
,
∴
,
∴当时,四边形的面积为,是一个定值.
【点睛】本题考查列代数式,矩形的性质,等腰三角形的定义,运用方程解决几何问题,整式的加减,综合运用相关知识是解题的关键.
22.(1)42,22
(2)剪去的正方形的边长为
(3)剪去的正方形的边长为
【分析】本题主要考查了一元二次方程的应用,长方体的展开和折叠,对于(1),根据题意计算即可;
对于(2),设减去正方形得边长为xcm,可知纸盒底面长方形得长为,宽为,根据题意列出一元二次方程,解方程即可;
对于(3),设剪去正方形得边长为acm,根据题意列出一元二次方程,求出解即可.
【详解】(1)由题意,得.
纸盒底面长方形得长为42cm,宽为22cm.
故答案为42,22;
(2)设减去正方形的边长为xcm,则纸盒底面长方形的长为,宽为,根据题意,得
,
解得(舍),
∴剪去正方形的边长为2cm;
(3)设正方形的边长为acm,
由题意,得,
解得或(舍).
∴剪去正方形得边长为3cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第2章一元二次方程例题精讲与跟踪训练-数学九年级上册北师大版
一、单选题
1.关于的方程是一元二次方程,则□可以是( )
A. B. C. D.
2.关于x的一元二次方程没有实数根,则实数m的取值范围是( )
A. B. C. D.
3.若是一元二次方程的一个解,则方程的另一个解为( )
A. B. C. D.
4.一元二次方程的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
5.探讨关于x的一元二次方程总有实数根的条件,下面三名同学给出建议:甲:a,b同号;乙:;丙:.其中符合条件的是( )
A.甲,乙,丙都正确 B.只有甲不正确
C.甲,乙,丙都不正确 D.只有乙不正确
6.将一元二次方程化成(a,b为常数)的形式,则a,b的值分别是( )
A. B. C.4,21 D.
7.武汉市某区2022年应届初中毕业生为5万人,2023年、2024年两届毕业生一共为12万人,设2022年到2024年平均每年学生人数增长的百分率为x,则方程可列为( )
A. B.
C. D.
8.如图,某摄影爱好者拍摄了一副长为,宽为的杭州金沙湖大剧院风景照,现在风景画四周一条等宽的纸边,制成一幅矩形挂图.若要使整幅挂图的面积是,设纸边的宽为(),则应满足的方程是( )
A. B.
C. D.
二、填空题
9.一元二次方程的解是 .
10.关于x的方程有两个相等的实数根,则k值为 .
11.若a是方程的一个根,则代数式的值为 .
12.已知实数、满足,,则的值为 .
13.有关部门决定降低药价,对某种原价为100元的药品进行连续两次降价后为81元.则平均每次降价的百分率为 .
14.如图,邻边不等的矩形花圃,它的一边利用已有的16m的围墙,另外三边所围的栅栏的总长度是32m,若矩形花圃的面积为,则的长度是 m.
15.等腰三角形的边长是方程的解,则这个三角形的周长是 .
16.对于实数,我们定义符号的意义为:当时,;当时,,如,则方程的解为 .
三、解答题
17.解方程:
(1);
(2).
18.已知关于x的一元二次方程.
(1)证明:无论为何值,方程总有两个不相等的实数根:
(2)若方程的两个实数根分别为,且,求的值.
19.某品牌纪念品每套成本为元,当售价为元时,平均每天的销售量为套,经试销统计发现,如果该品牌纪念品售价每上涨元,那么平均每天的销售量将减少套,为了维护消费者利益,物价部门规定:该品牌纪念品售价不能超过进价的,商家想要使这种纪念品的销售利润平均每天达到元,求每套纪念品应定价多少元?
20.如图,某农场老板准备建造一个矩形养兔场,他打算让矩形养兔场的一边完全靠着墙,墙可利用的长度为24米,另外三面用长度为50米的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分),设矩形垂直于墙的边的长为x 米,矩形的面积记为y平方米.
(1)当时, 米, 平方米;
(2)若要使矩形养兔场的面积为300平方米,则垂直于墙的一边的长为多少米?
21.在矩形中,,一动点从点出发沿着方向以的速度运动,另一动点从点A出发沿着边以的速度运动,两点同时出发,运动时间为.
(1)当为何值时为等腰三角形?
(2)若的面积是矩形面积的,求的值;
(3)的面积能否等于五边形面积的?若能,求出的值;若不能,说明理由;
(4)当时,求证:四边形的面积是一个定值.
22.综合与实践
用矩形硬纸片制作无盖纸盒.如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若剪去的正方形的边长为,则纸盒底面长方形的长为_______,宽为_____;
(2)若纸盒的底面积为,请计算剪去的正方形的边长;
(3)如图3,先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 A A A B B A D D
1.A
【分析】本题主要考查一元二次方程的定义,判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.根据一元二次方程的定义判断作答即可.
【详解】解:A.,是一元二次方程,此选项符合题意;
B.,是二元二次方程,此选项不符合题意;
C.,是二元二次方程,此选项不符合题意;
D.,是一元一次方程,此选项不符合题意;
故选:A.
2.A
【分析】本题考查了一元二次方程根的判别式.根据一元二次方程根的判别式小于0,方程没有实数根,列不等式计算即可.
【详解】解:关于x的一元二次方程化为一般式为,
根据题意得:,
即,
解得:,
故选:A.
3.A
【分析】此题主要考查了一元二次方程根与系数的关系,解题的关键是熟练掌握一元二次方程根与系数的关系.根据根与系数的关系即可求解.
【详解】解:设方程的另一个根为,
则,
∴.
故选:A.
4.B
【分析】本题主要考查了根的判别式,一元二次方程,当时,方程有两个不相等的实数根;当时,方程没有实数根;当时,方程有两个相等的实数根.
先求出一元二次方程根的判别式的值,然后判断即可.
【详解】解:∵一元二次方程,
∴,
∴方程有两个不相等的实数根.
故选:B.
5.B
【分析】本题考查一元二次方程有实数根的条件,根据题中所给条件,结合一元二次方程根的判别式讨论是解决问题的关键.
根据一元二次方程根的判别式求解,然后根据各种说法的条件逐项验证即可.
【详解】解:关于x的一元二次方程根的判别式为:,
甲:当a,b同号时,若两数均为负数,就不能确保的符号为正,不符合题意;
乙:当时,得到,从而,总有实数根,符合题意;
丙:当时,得到,从而,总有实数根,符合题意;
综上所述,甲的建议不能满足题意,乙和丙的建议满足题意,
故选:B.
6.A
【分析】本题考查了用配方法解一元二次方程,能正确配方是解此题的关键.将常数项移到方程的右边,两边都加上一次项系数一半的平方配成完全平方式后即可得出答案.
【详解】解:,
,
则,
即,
,,
故选:A.
7.D
【分析】本题考查了由实际问题抽象出一元二次方程,平均每年学生人数增长的百分率为x,根据2023年、2024年年两届毕业生一共为万人,即可得出关于x 的一元二次方程,此题得解.
【详解】解:平均每年学生人数增长的百分率为x,方程可列为,
故选:D.
8.D
【分析】本题考查了一元二次方程的应用.根据题意正确的列方程是解题的关键.
依题意得,面积为,然后作答即可.
【详解】解:由题意知,矩形挂图的长为,宽为,
依题意得,面积为,
故选:D.
9.
【分析】本题主要考查了解一元二次方程.熟练掌握因式分解法解一元二次方程,是解决问题的关键.
移项,提公因式x,化成两个一元一次方程解答即可.
【详解】∵,
∴移项得,,
分解因式得,,
∴,
∴.
故答案为:.
10.
【分析】本题考查了一元二次方程根的判别式,对于一元二次方程,当时,一元二次方程有两个不相等的实数根;当时,一元二次方程有两个相等的实数根;当时,一元二次方程没有实数根.
【详解】解:∵方程有两个相等的实数根,
∴,即,
解得:,
故答案为:.
11.7
【分析】本题考查了一元二次方程的解、求代数式的值,由题意得出,推出,整体代入计算即可得出答案.
【详解】解:∵a是方程的一个根,
∴,
∴,
∴,
故答案为:.
12.或2
【分析】本题考查一元二次方程根与系数的关系,根据题意可知,实数是一元二次方程的实数根,再根据一元二次方程根与系数的关系及方程相等的两实数根解题即可.
【详解】解:依题意,实数是一元二次方程的实数根,
若,则
;
若,则
故答案为:或2.
13.10%
【分析】本题主要考查求平均变化率的方法、解一元二次方程,若设变化前的量为,变化后的量为,平均变化率为,则经过两次变化后的数量关系为:,解题的关键是熟记公式并应用.
设平均每次降价的百分率为,根据题意和公式即可列出方程,求解即可.
【详解】解:设平均每次降价的百分率为,
由题意得:,
解得:或(舍去),
平均每次降价的百分率为10%.
故答案为:10%.
14.10
【分析】本题考查一元二次方程的应用,设,根据矩形的面积公式,列出一元二次方程,进行求解即可.
【详解】解:设,则:,由题意,得:
,
解得:,
当时,,不符合题意,舍去
当时,,符合题意;
故的长度是;
故答案为:10
15.11或13/13或11
【分析】本题主要考查了等腰三角形的定义,构成三角形的条件,解一元二次方程,先利用因式分解法求出方程的解为或,再分当腰长为3时,当腰长为5时,两种情况根据构成三角形的条件讨论求解即可.
【详解】解:解方程得:或,
当腰长为3时,则等腰三角形的三边长为3,3,5,
∵,
∴此时能构成三角形,
∴这个三角形的周长是;
当腰长为5时,则等腰三角形的三边长为3,5,5,
∵,
∴此时能构成三角形,
∴这个三角形的周长是;
综上所述,这个三角形的周长是11或13,
故答案为:11或13.
16.或3
【分析】本题主要考查了新定义,解一元二次方程,解题的关键是正确理解题目所给新定义的运算法则,以及解一元二次方程的方法和步骤.根据题目所给新定义,列出方程求解即可.
【详解】解:, ,
∴,即,
解得:,
故答案为:或3.
17.(1),
(2)
【分析】本题考查了解一元二次方程,熟练掌握各种解法是解题的关键.
(1)因式分解法求解即可;
(2)公式法求解即可.
【详解】(1)解:,
或,
解得:或,
∴原方程的根为:,;
(2)解:
,
∴,
∴原方程的根为:.
18.(1)证明见解析
(2)
【分析】本题主要考查了一元二次方程根的判别式,根与系数的关系:
(1)只需要证明即可;
(2)根据根与系数的关系得到,,再由已知条件建立方程组求出,据此代值计算即可.
【详解】(1)证明:由题意得,,
∵,
∴,
∴无论为何值,方程总有两个不相等的实数根:
(2)解:∵关于x的一元二次方程的两个实数根分别为,
∴,
又∵,
∴,
解得,
∴,
∴.
19.元
【分析】本题考查了一元二次方程的应用,设每套纪念品应定价为元,根据题意列出方程组,求出的值,再结合售价不能超过进价的进行判断即可求解,根据题意正确列出方程是解题的关键.
【详解】解:设每套纪念品应定价为元,
由题意得,,
解得,,
当时,,符合题意,
当时,,不合题意,
∴,
答:每套纪念品应定价为元.
20.(1)10;200
(2)的长为15米
【分析】本题考查了一元二次方程的实际应用.
(1)根据题意可得,即可求出,根据长方形面积公式,即可求出y;
(2)根据题意可得,则,根据长方形面积公式,列出方程求解即可.
【详解】(1)解:当时,,
,
故答案为:10,200;
(2)解:由题意知:,则,
∴,
整理得:,
解得:,,
当时,,应舍去,
∴的长为15米.
21.(1)
(2)
(3)不能,理由见解析
(4)见解析
【分析】(1)用含t的式子表示,,的长,根据为等腰三角形得到,代入后解方程即可;
(2)表示出和矩形的面积,根据的面积是矩形面积的,即可列出方程,求解即可;
(3)当时,,代入后得到一元二次方程,根据一元二次方程根的判别式即可解答;
(4)表示出和的面积,根据,代入后化简即可得证.
【详解】(1)解:当运动时,,,
∴,
∵在矩形中,
∴当为等腰三角形时,,
∴,
解得;
(2)解:∵,
,
∴当时,,
解得;
(3)解:当时,,
∵,,
∴,
整理,得,
∵,
∴方程没有实数根,
∴的面积不能等于五边形面积的;
(4)证明:∵四边形是矩形,
∴,,
∵当运动时,,,,,
∴,
,
∴
,
∴当时,四边形的面积为,是一个定值.
【点睛】本题考查列代数式,矩形的性质,等腰三角形的定义,运用方程解决几何问题,整式的加减,综合运用相关知识是解题的关键.
22.(1)42,22
(2)剪去的正方形的边长为
(3)剪去的正方形的边长为
【分析】本题主要考查了一元二次方程的应用,长方体的展开和折叠,对于(1),根据题意计算即可;
对于(2),设减去正方形得边长为xcm,可知纸盒底面长方形得长为,宽为,根据题意列出一元二次方程,解方程即可;
对于(3),设剪去正方形得边长为acm,根据题意列出一元二次方程,求出解即可.
【详解】(1)由题意,得.
纸盒底面长方形得长为42cm,宽为22cm.
故答案为42,22;
(2)设减去正方形的边长为xcm,则纸盒底面长方形的长为,宽为,根据题意,得
,
解得(舍),
∴剪去正方形的边长为2cm;
(3)设正方形的边长为acm,
由题意,得,
解得或(舍).
∴剪去正方形得边长为3cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
