沪科版数学八年级下册 19.1 多边形内角和&19.2 平行四边形 基础复习(一)(含答案)
文档属性
| 名称 | 沪科版数学八年级下册 19.1 多边形内角和&19.2 平行四边形 基础复习(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 743.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览


文档简介
第 19 章基础复习(一)
知识点 1 多边形内角和
1. 多边形中连接不相邻两个顶点的线段叫做多边形的对角线.
2. n边形的内角和等于(n-2)·180°(n为不小于3的整数).
3. n边形的外角和等于360°(n为不小于3的整数).
4. 多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形.
5. 四边形具有不稳定性.
1. 六边形的内角和为 ( )
A.360° B.540° C.720° D.1080°
2. 正十边形的每一个外角的度数为 ( )
A.36° B.30° C.144° D.150°
3. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转 ,…照这样走下去,他第一次回到出发点A时,共走路程为 ( )
A.80米 B.96米 C.64米 D.48米
4. 如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形 BCDEMN,则∠1+∠2的度数为 ( )
B.110° C.150° D.100°
5. 一个正n边形的内角和是它外角和的4倍,则n= .
6. 如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC= 度.
7. 如图,在正五边形ABCDE 中,DM 是边 CD 的延长线,连接BD,则∠BDM 的度数是 .
8. 已知一个多边形的所有内角的和与它的外角之和为1 620°,求这个多边形的边数.
9. 如图,四边形ABCD中, ,BE平分 ,DF 平分 ,BE,CD交于点 G.
(2)求证:
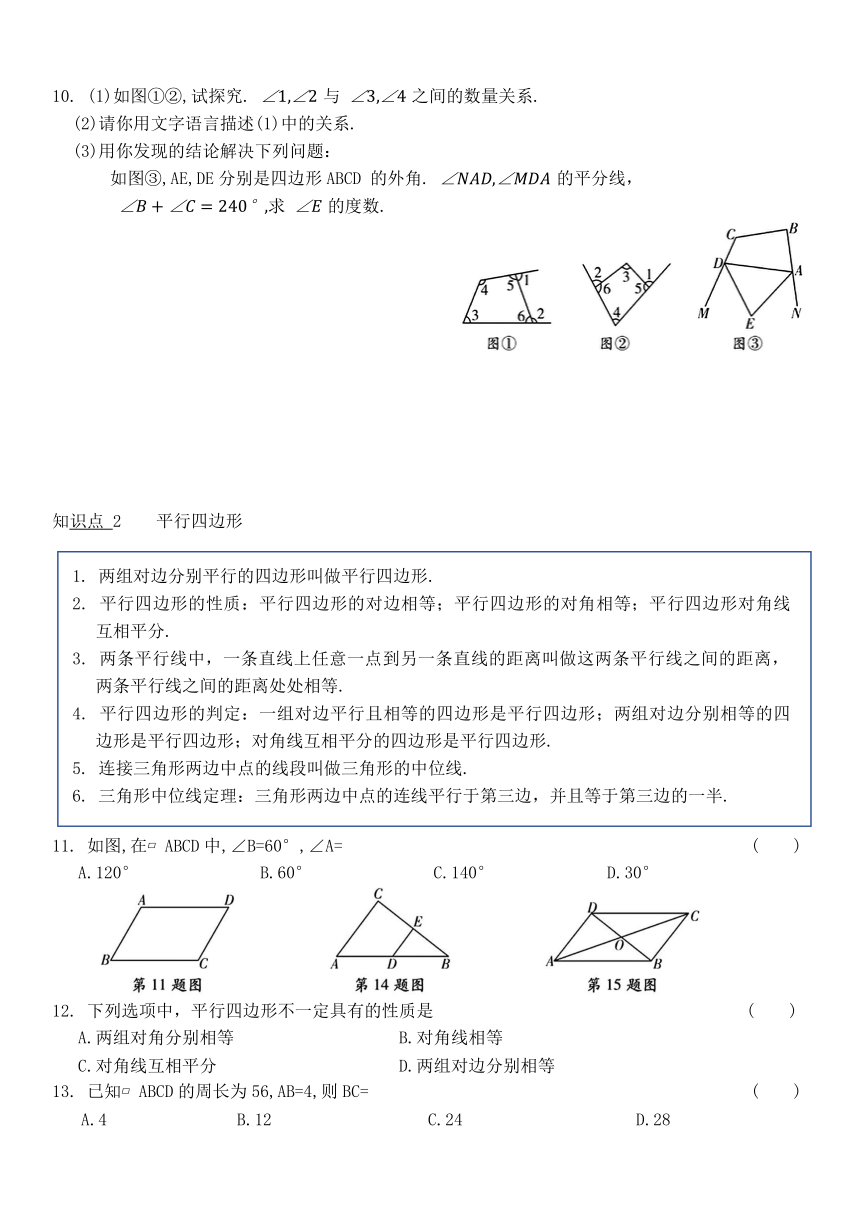
10. (1)如图①②,试探究. 与 之间的数量关系.
(2)请你用文字语言描述(1)中的关系.
(3)用你发现的结论解决下列问题:
如图③,AE,DE分别是四边形ABCD 的外角. 的平分线,
求 的度数.
知识点 2 平行四边形
1. 两组对边分别平行的四边形叫做平行四边形.
2. 平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形对角线互相平分.
3. 两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离,两条平行线之间的距离处处相等.
4. 平行四边形的判定:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
5. 连接三角形两边中点的线段叫做三角形的中位线.
6. 三角形中位线定理:三角形两边中点的连线平行于第三边,并且等于第三边的一半.
11. 如图,在 ABCD中,∠B=60°,∠A= ( )
A.120° B.60° C.140° D.30°
12. 下列选项中,平行四边形不一定具有的性质是 ( )
A.两组对角分别相等 B.对角线相等
C.对角线互相平分 D.两组对边分别相等
13. 已知 ABCD的周长为56,AB=4,则BC= ( )
A.4 B.12 C.24 D.28
14. 如图,在△ABC中,AC=8,DE是△ABC的中位线,则DE的长度是 ( )
A.4 B.5 C.6 D.3
15. 如图,在四边形 ABCD中,对角线AC,BD 相交于点 O,下列条件中能够判定这个四边形是平行四边形的是 ( )
A. AB∥DC,AD=BC B. AB=AD,CD=CB
C. AO=BO,DO=CO D. AO=CO,BO=DO
16. 已知平行四边形两邻边长为16,20,若两个长边间距离为8,则两条短边间距离为 ( )
A.4 B.5 C.10 D.8
17. 如图,在四边形ABCD中,连接AC,∠ACB =∠CAD.请你添加一个条件 ,使AB=CD.(填一种情况即可)
18. 如图, ABCD 的对角线AC,BD 相交于点O,OE∥AB交AD 于点 E,若 OA =1,△AOE的周长等于5,则 ABCD的周长等于 .
19. 如图, ABCD 中,∠ADC=120°,BE⊥DC于点E,DF⊥BC于点 F,BE与DF交于点 H,则∠BHF= 度.
20. 如图,E是平行四边形 ABCD 内任意一点,若平行四边形 ABCD 的面积是6,则阴影部分的面积是 .
21. 如图,在四边形 BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.当BC=4,DE=5,∠FMN=45°时,BE的长为 .
22. 如图, 中,点E,F分别在BC,DE上, 求证:
23. 如图,在四边形ABCD 中,P是对角线BD的中点,E,F分别是AB,CD的中点, 求 的度数.
24. 如图,在 中, 于点E,在EF上取一点 B,连接AB,BC,使得 过点A作 且 连接CD.
(1)如图1,求证:四边形ABCD是平行四边形.
(2)如图2,若AB平分 ,延长FE交CD于点H,请直接写出与 相等的角.
第19章基础复习(一)
1. C 2. A 3. C 4. A 5. 10 6. 30 7. 144°
8. 解:设这个多边形的边数是n,由题意,得(n﹣2)·180°+360°=1 620°,解得n=9.
答:这个多边形的边数n是9.
9. (1)解:∵ 在四边形ABCD中,∠A=∠C=90°,∠A+∠ABC+∠C+∠ADC=360°,
∴∠ABC+∠ADC=180°.故答案为:180°.
(2)证明:∵BE平分∠ABC,DF平分∠ADC,
∵∠ABC+∠ADC=180°,∴∠GBC+∠CDF=90°.
∵∠C+∠CDF+∠DFC=180°,∠C=90°,
∴∠CDF+∠DFC=90°,∴∠GBC=∠DFC,
∴BG∥DF,∴∠G=∠CDF.
10. 解:(1)∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,∴∠MDA+∠NAD=240°,
∵AE,DE分别是∠NAD,∠MDA的平分线,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
11. A 12. B 13. C 14. A 15. D 16. C
17. AD=BC(答案不唯一) 18. 16 19. 60 20. 3
22. 证明:∵ 四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∴∠ADF=∠DEC.
∵ AF = AB, ∴ AF = DC, 在 △DFA 和 △ECD
中
∴△DFA≌△ECD(AAS),∴AD =DE.
23. 解:∵P是BD的中点,E是AB的中点,∴PE是△ABD的中位线,∴
同理,PF= BC,∵AD=BC,∴PE=PF,∴∠PFE=∠PEF=20°.
24. (1)证明:∵FE⊥AC,∴∠FEA=∠FEC=90°,
∵∠FAC=45°,∴△AEF是等腰直角三角形,
∴AE=EF,∠AFE=∠FAE=45°,
在Rt△AEB和Rt△FEC中,
∴Rt△AEB≌Rt△FEC(HL),∴BE=CE,
∴∠CBE=∠BCE=45°.
∵AD⊥AF,∴∠FAD=90°,∴∠CAD=90°-∠FAC=45°,
∴∠BCE=∠CAD,∴BC∥AD.
又∵BC=AD,∴四边形ABCD是平行四边形.
(2)解:与∠ABE相等的角有:∠CHB,∠BCD,∠BAD,∠FCA,∠CFA,理由如下:
由(1)得:Rt△AEB≌Rt△FEC,四边形ABCD是平行四边形,
∴∠BAE=∠CFE,∠FCE=∠ABE,∠BCH=∠BAD,AB∥CD,
∴∠CHB=∠ABE,∠BAE=∠DCA,
∵AB平分∠FAC,∠FAC=45°,∴∠BAC=∠BAF=22.5°,
∴∠ABE=90°-22.5°=67.5°,∠CFE=22.5°,∠DCA=22.5°,
∴∠FCA=90°-∠CFE=67.5°,
又∵∠AFH=∠BCE=∠CAD=45°,
∴∠CFA=∠BCD=∠BAD=67.5°,
∴∠FCA=∠CFA=∠BCD=∠BAD =∠ABE.
综 上, 与 ∠ABE 相 等 的 角 为 ∠CHB, ∠BCD, ∠BAD,∠FCA,∠CFA.
知识点 1 多边形内角和
1. 多边形中连接不相邻两个顶点的线段叫做多边形的对角线.
2. n边形的内角和等于(n-2)·180°(n为不小于3的整数).
3. n边形的外角和等于360°(n为不小于3的整数).
4. 多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形.
5. 四边形具有不稳定性.
1. 六边形的内角和为 ( )
A.360° B.540° C.720° D.1080°
2. 正十边形的每一个外角的度数为 ( )
A.36° B.30° C.144° D.150°
3. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转 ,…照这样走下去,他第一次回到出发点A时,共走路程为 ( )
A.80米 B.96米 C.64米 D.48米
4. 如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形 BCDEMN,则∠1+∠2的度数为 ( )
B.110° C.150° D.100°
5. 一个正n边形的内角和是它外角和的4倍,则n= .
6. 如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC= 度.
7. 如图,在正五边形ABCDE 中,DM 是边 CD 的延长线,连接BD,则∠BDM 的度数是 .
8. 已知一个多边形的所有内角的和与它的外角之和为1 620°,求这个多边形的边数.
9. 如图,四边形ABCD中, ,BE平分 ,DF 平分 ,BE,CD交于点 G.
(2)求证:
10. (1)如图①②,试探究. 与 之间的数量关系.
(2)请你用文字语言描述(1)中的关系.
(3)用你发现的结论解决下列问题:
如图③,AE,DE分别是四边形ABCD 的外角. 的平分线,
求 的度数.
知识点 2 平行四边形
1. 两组对边分别平行的四边形叫做平行四边形.
2. 平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形对角线互相平分.
3. 两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离,两条平行线之间的距离处处相等.
4. 平行四边形的判定:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
5. 连接三角形两边中点的线段叫做三角形的中位线.
6. 三角形中位线定理:三角形两边中点的连线平行于第三边,并且等于第三边的一半.
11. 如图,在 ABCD中,∠B=60°,∠A= ( )
A.120° B.60° C.140° D.30°
12. 下列选项中,平行四边形不一定具有的性质是 ( )
A.两组对角分别相等 B.对角线相等
C.对角线互相平分 D.两组对边分别相等
13. 已知 ABCD的周长为56,AB=4,则BC= ( )
A.4 B.12 C.24 D.28
14. 如图,在△ABC中,AC=8,DE是△ABC的中位线,则DE的长度是 ( )
A.4 B.5 C.6 D.3
15. 如图,在四边形 ABCD中,对角线AC,BD 相交于点 O,下列条件中能够判定这个四边形是平行四边形的是 ( )
A. AB∥DC,AD=BC B. AB=AD,CD=CB
C. AO=BO,DO=CO D. AO=CO,BO=DO
16. 已知平行四边形两邻边长为16,20,若两个长边间距离为8,则两条短边间距离为 ( )
A.4 B.5 C.10 D.8
17. 如图,在四边形ABCD中,连接AC,∠ACB =∠CAD.请你添加一个条件 ,使AB=CD.(填一种情况即可)
18. 如图, ABCD 的对角线AC,BD 相交于点O,OE∥AB交AD 于点 E,若 OA =1,△AOE的周长等于5,则 ABCD的周长等于 .
19. 如图, ABCD 中,∠ADC=120°,BE⊥DC于点E,DF⊥BC于点 F,BE与DF交于点 H,则∠BHF= 度.
20. 如图,E是平行四边形 ABCD 内任意一点,若平行四边形 ABCD 的面积是6,则阴影部分的面积是 .
21. 如图,在四边形 BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.当BC=4,DE=5,∠FMN=45°时,BE的长为 .
22. 如图, 中,点E,F分别在BC,DE上, 求证:
23. 如图,在四边形ABCD 中,P是对角线BD的中点,E,F分别是AB,CD的中点, 求 的度数.
24. 如图,在 中, 于点E,在EF上取一点 B,连接AB,BC,使得 过点A作 且 连接CD.
(1)如图1,求证:四边形ABCD是平行四边形.
(2)如图2,若AB平分 ,延长FE交CD于点H,请直接写出与 相等的角.
第19章基础复习(一)
1. C 2. A 3. C 4. A 5. 10 6. 30 7. 144°
8. 解:设这个多边形的边数是n,由题意,得(n﹣2)·180°+360°=1 620°,解得n=9.
答:这个多边形的边数n是9.
9. (1)解:∵ 在四边形ABCD中,∠A=∠C=90°,∠A+∠ABC+∠C+∠ADC=360°,
∴∠ABC+∠ADC=180°.故答案为:180°.
(2)证明:∵BE平分∠ABC,DF平分∠ADC,
∵∠ABC+∠ADC=180°,∴∠GBC+∠CDF=90°.
∵∠C+∠CDF+∠DFC=180°,∠C=90°,
∴∠CDF+∠DFC=90°,∴∠GBC=∠DFC,
∴BG∥DF,∴∠G=∠CDF.
10. 解:(1)∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6),
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,∴∠MDA+∠NAD=240°,
∵AE,DE分别是∠NAD,∠MDA的平分线,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
11. A 12. B 13. C 14. A 15. D 16. C
17. AD=BC(答案不唯一) 18. 16 19. 60 20. 3
22. 证明:∵ 四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,∴∠ADF=∠DEC.
∵ AF = AB, ∴ AF = DC, 在 △DFA 和 △ECD
中
∴△DFA≌△ECD(AAS),∴AD =DE.
23. 解:∵P是BD的中点,E是AB的中点,∴PE是△ABD的中位线,∴
同理,PF= BC,∵AD=BC,∴PE=PF,∴∠PFE=∠PEF=20°.
24. (1)证明:∵FE⊥AC,∴∠FEA=∠FEC=90°,
∵∠FAC=45°,∴△AEF是等腰直角三角形,
∴AE=EF,∠AFE=∠FAE=45°,
在Rt△AEB和Rt△FEC中,
∴Rt△AEB≌Rt△FEC(HL),∴BE=CE,
∴∠CBE=∠BCE=45°.
∵AD⊥AF,∴∠FAD=90°,∴∠CAD=90°-∠FAC=45°,
∴∠BCE=∠CAD,∴BC∥AD.
又∵BC=AD,∴四边形ABCD是平行四边形.
(2)解:与∠ABE相等的角有:∠CHB,∠BCD,∠BAD,∠FCA,∠CFA,理由如下:
由(1)得:Rt△AEB≌Rt△FEC,四边形ABCD是平行四边形,
∴∠BAE=∠CFE,∠FCE=∠ABE,∠BCH=∠BAD,AB∥CD,
∴∠CHB=∠ABE,∠BAE=∠DCA,
∵AB平分∠FAC,∠FAC=45°,∴∠BAC=∠BAF=22.5°,
∴∠ABE=90°-22.5°=67.5°,∠CFE=22.5°,∠DCA=22.5°,
∴∠FCA=90°-∠CFE=67.5°,
又∵∠AFH=∠BCE=∠CAD=45°,
∴∠CFA=∠BCD=∠BAD=67.5°,
∴∠FCA=∠CFA=∠BCD=∠BAD =∠ABE.
综 上, 与 ∠ABE 相 等 的 角 为 ∠CHB, ∠BCD, ∠BAD,∠FCA,∠CFA.
