沪科版数学八年级下册 19.3矩形、菱形、正方形&19.4 多边形的镶嵌 基础复习(二)(含答案)
文档属性
| 名称 | 沪科版数学八年级下册 19.3矩形、菱形、正方形&19.4 多边形的镶嵌 基础复习(二)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 691.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览


文档简介
第 19 章基础复习(二)
知识点 1 矩形、菱形、正方形
1. 矩形的定义与性质:定义:有一个角是直角的平行四边形叫做矩形.性质1:矩形的四个角都是直角.性质2:矩形的对角线相等.
2. 直角三角形斜边上的中线等于斜边的一半.
3. 矩形的判定:①有一个角是直角的平行四边形是矩形.②对角线相等的平行四边形是矩形.③三个角是直角的四边形是矩形.
4. 菱形的定义与性质:定义:有一组邻边相等的平行四边形叫做菱形.性质1:菱形的四条边都相等.性质2:菱形的对角线互相垂直.
5. 菱形的判定:①有一组邻边相等的平行四边形是菱形.②四边都相等的四边形是菱形.③对角线互相垂直的平行四边形是菱形.
6. 正方形的定义与性质:定义:有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.性质1:正方形的四条边都相等,四个角都是直角.性质2:正方形的对角线相等且互相垂直平分.
1. 在Rt△ABC中,∠C=90°,若D为斜边AB上的中点,AB的长为6,则DC的长为 ( )
A.4 B.3 C.2 D.1
2. 下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是 ( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出② D.由①推出③,由③推出②
3. 若菱形两条对角线的乘积等于48,则这个菱形的面积为 ( )
A.48 B.32 C.24 D.12
4. 如图,将矩形纸片 ABCD 沿 BE 折叠,使点 A 落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于 ( )
A.66° B.60°
C.57° D.48°
5. 已知四边形ABCD是平行四边形,AC,BD相交于点 O,下列结论错误的是 ( )
A. OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
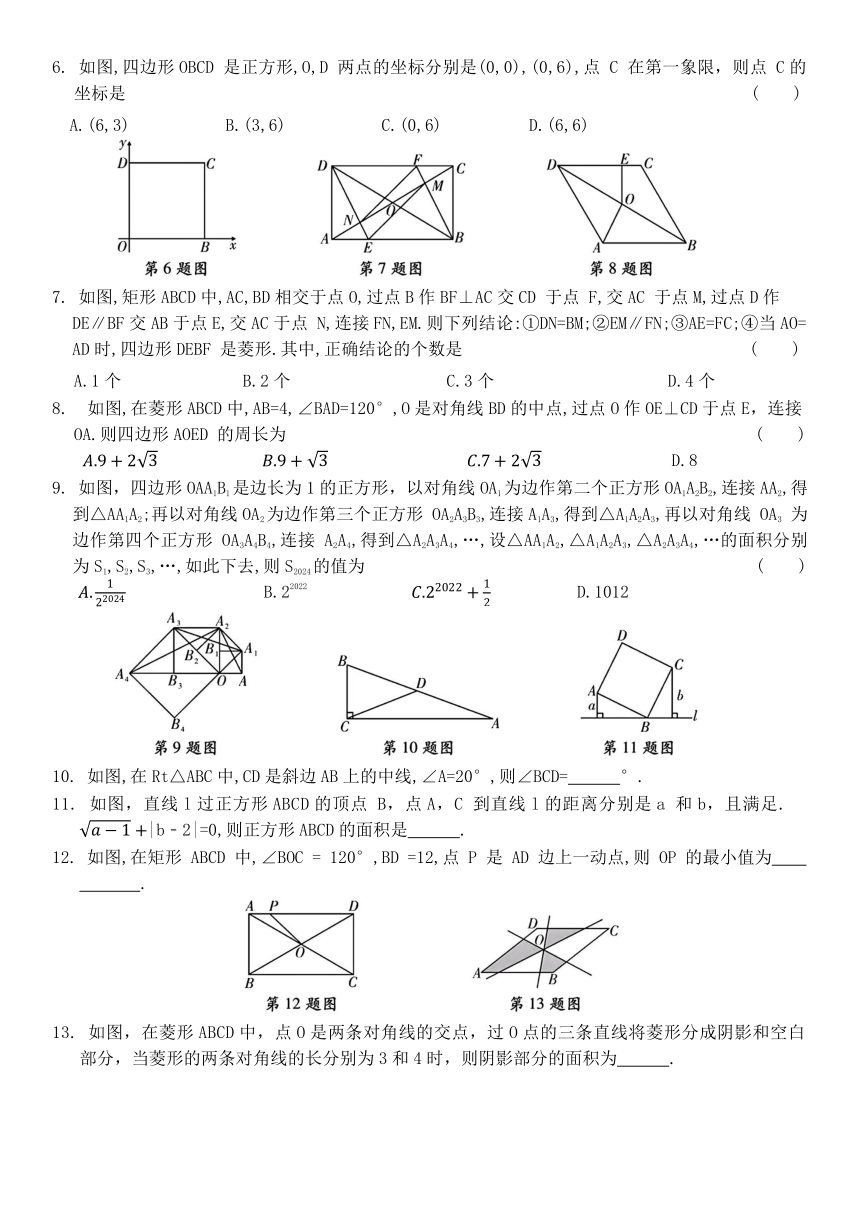
6. 如图,四边形OBCD 是正方形,O,D 两点的坐标分别是(0,0),(0,6),点 C 在第一象限,则点 C的坐标是 ( )
A.(6,3) B.(3,6) C.(0,6) D.(6,6)
7. 如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD 于点 F,交AC 于点M,过点D作 DE∥BF交AB于点E,交AC于点 N,连接FN,EM.则下列结论:①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF 是菱形.其中,正确结论的个数是 ( )
A.1个 B.2个 C.3个 D.4个
8. 如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于点E,连接OA.则四边形AOED 的周长为 ( )
D.8
9. 如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△AA1A2;再以对角线OA2为边作第三个正方形 OA2A3B3,连接A1A3,得到△A1A2A3,再以对角线 OA3 为边作第四个正方形 OA3A4B4,连接 A2A4,得到△A2A3A4,…,设△AA1A2,△A1A2A3,△A2A3A4,…的面积分别为S1,S2,S3,…,如此下去,则S2024的值为 ( )
B.22022 D.1012
10. 如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD= °.
11. 如图,直线l过正方形ABCD的顶点 B,点A,C 到直线l的距离分别是a 和b,且满足. |b﹣2|=0,则正方形ABCD的面积是 .
12. 如图,在矩形 ABCD 中,∠BOC = 120°,BD =12,点 P 是 AD 边上一动点,则 OP 的最小值为 .
13. 如图,在菱形ABCD中,点O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为3和4时,则阴影部分的面积为 .
14. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM①点 M位置变化,使得∠DHC=60°时,
②无论点M运动到何处,都有
③在点 M的运动过程中,四边形 CEMD 可能成为菱形;
④无论点 M 运动到何处,∠CHM一定大于
以上结论正确的有 (把所有正确结论的序号都填上).
15. 如图,在菱形ABCD中,将对角线AC分别向两端延长到点E和F,使得 连接DE,DF,BE,BF.求证:四边形BEDF是菱形.
16. 如图,在矩形ABCD中,过对角线BD的中点O 作 BD的垂线EF,分别交AD,BC于点 E,F.
(1)求证:
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE 的周长.
17. 如图,已知四边形ABCD为正方形, ,点E为对角线AC上一动点,连接DE,过点E 作EF ,交BC于点F,以 DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG 是正方形.
(2)探究:的值是否为定值 若是,请求出这个定值;若不是,请说明理由.
知识点 2 多边形的镶嵌
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
18. 下列正多边形中,能够铺满地面的是 ( )
A.正方形 B.正五边形 C.正八边形 D.正十边形
19. 用三块正多边形的木板铺地,拼在一起的三块正多边形木板相交于一点且各边完全吻合,其中两块木板的边数都是5,则第三块木板的边数是 ( )
A.5 B.6 C.8 D.10
20. 在下列四组多边形的地板砖中:①正三角形与正方形;②正三角形与正十边形;③正方形与正六边形;④正方形与正八边形.将每组中的两种多边形结合,能密铺地面的是 ( )
A.①②③ B.①②④ C.③④ D.①④
21. 利用边长相等的正三角形和正六边形地砖能够铺满地板,若在每个顶点处有a块正三角形和b块正六边形(a>b>0),则a+b的值为 ( )
A.4 B.5 C.6 D.7
22. 用形状、大小完全相同的正三角形作平面镶嵌,则每个拼接点的周围有 个正三角形.
23. 在一个顶点处用边长相等的三个正多边形进行密铺,其中两个是正方形和正六边形,则另一个必须是正 边形.
24. 如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6 个正三角形,第2层包括6个正方形和18个正三角形,…,依此递推,则第6层中含有正三角形个数是 ,第n层中含有正三角形个数是 .
25. 在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:
(1)用一种正多边形镶嵌平面
例如,用6个全等的正三角形镶嵌平面,摆放方案如图所示:
若用m个全等的正n边形镶嵌平面,求出m,n应满足的关系式.
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案.
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有n个,设这n个正多边形的边数分别为: 求出x1,x2,…,x 应满足的关系式.(用含n的式子表示)
第19 章基础复习(二)
1. B 2. A 3. C 4. C 5. B 6. D 7. D 8. B 9. B10. 70 11.5 12. 3 13. 3
14. ①②④
15. 证明:∵ 四边形ABCD是菱形,∴BC=CD,∠DCA=∠BCA,∴∠DCF=∠BCF.∵CF=CF,∴△CDF≌△CBF(SAS),∴DF=BF,∵AD∥BC,∴∠DAC=∠BCA,∴∠DAE=∠BCF,
∵AE=CF,DA=BC,∴△DAE≌△BCF(SAS),∴DE=BF,同理可证:△DCF≌△BAE(SAS),∴DF=BE,∴DF=BF=BE=DE,∴四边形BEDF是菱形.
16. (1)证明:∵ 四边形ABCD是矩形,∴AD∥BC,∴∠EDO=∠FBO.又∵EF⊥BD,∴∠EOD=∠FOB=90°,又∵O为BD中点,∴DO=BO,在△DOE和△BOF中, ∴△DOE≌△BOF(ASA).
(2)解:由(1)可得,ED∥BF,ED=BF,∴四边形BFDE是平行四边形.∵EF⊥BD,∴四边形BFDE是菱形,设AE=x,则BE=ED=8-x,在Rt△ABE中,根据勾股定理,得 即 解得 ∴四边形BFDE的周长为
17. (1)证明:如图,过点E作EM⊥BC于点M,EN⊥CD于点 N,则∠DNE=∠FME=90°,
∵ 四边形 ABCD 是正方形,
∴∠BCD=90°,∴∠MEN=90°,
∵ 点E是正方形ABCD对角线上的点,
∴EM=EN,
∵ 四边形 DEFG是矩形,∴∠DEF=90°,
∴∠DEN=∠FEM,在△DNE和△FME中,
∴△DEN≌△FEM(ASA),∴EF=ED,
∵ 四边形DEFG是矩形,∴矩形DEFG是正方形.
(2)解:CE+CG的值是定值,定值为6.理由如下:
∵ DE=DG,AD=DC,∠ADC=∠EDG=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
∴△ADE≌△CDG(SAS),∴AE=CG,
∴CE+CG的值是定值6.
18. A 19. D 20. D 21. B 22. 6 23. 12 24. 66 12n-6
25. 解:(1)∵正n边形的内角和为:180°(n-2),∴每个内角的度
数为: 由题意,得
即
(2)边长相等的正三角形和正方形镶嵌平面,有两种不同的摆放方案,如图所示:
(3)由题意,得
整理得
即
知识点 1 矩形、菱形、正方形
1. 矩形的定义与性质:定义:有一个角是直角的平行四边形叫做矩形.性质1:矩形的四个角都是直角.性质2:矩形的对角线相等.
2. 直角三角形斜边上的中线等于斜边的一半.
3. 矩形的判定:①有一个角是直角的平行四边形是矩形.②对角线相等的平行四边形是矩形.③三个角是直角的四边形是矩形.
4. 菱形的定义与性质:定义:有一组邻边相等的平行四边形叫做菱形.性质1:菱形的四条边都相等.性质2:菱形的对角线互相垂直.
5. 菱形的判定:①有一组邻边相等的平行四边形是菱形.②四边都相等的四边形是菱形.③对角线互相垂直的平行四边形是菱形.
6. 正方形的定义与性质:定义:有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.性质1:正方形的四条边都相等,四个角都是直角.性质2:正方形的对角线相等且互相垂直平分.
1. 在Rt△ABC中,∠C=90°,若D为斜边AB上的中点,AB的长为6,则DC的长为 ( )
A.4 B.3 C.2 D.1
2. 下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是 ( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出② D.由①推出③,由③推出②
3. 若菱形两条对角线的乘积等于48,则这个菱形的面积为 ( )
A.48 B.32 C.24 D.12
4. 如图,将矩形纸片 ABCD 沿 BE 折叠,使点 A 落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于 ( )
A.66° B.60°
C.57° D.48°
5. 已知四边形ABCD是平行四边形,AC,BD相交于点 O,下列结论错误的是 ( )
A. OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
6. 如图,四边形OBCD 是正方形,O,D 两点的坐标分别是(0,0),(0,6),点 C 在第一象限,则点 C的坐标是 ( )
A.(6,3) B.(3,6) C.(0,6) D.(6,6)
7. 如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD 于点 F,交AC 于点M,过点D作 DE∥BF交AB于点E,交AC于点 N,连接FN,EM.则下列结论:①DN=BM;②EM∥FN;③AE=FC;④当AO=AD时,四边形DEBF 是菱形.其中,正确结论的个数是 ( )
A.1个 B.2个 C.3个 D.4个
8. 如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于点E,连接OA.则四边形AOED 的周长为 ( )
D.8
9. 如图,四边形OAA1B1是边长为1的正方形,以对角线OA1为边作第二个正方形OA1A2B2,连接AA2,得到△AA1A2;再以对角线OA2为边作第三个正方形 OA2A3B3,连接A1A3,得到△A1A2A3,再以对角线 OA3 为边作第四个正方形 OA3A4B4,连接 A2A4,得到△A2A3A4,…,设△AA1A2,△A1A2A3,△A2A3A4,…的面积分别为S1,S2,S3,…,如此下去,则S2024的值为 ( )
B.22022 D.1012
10. 如图,在Rt△ABC中,CD是斜边AB上的中线,∠A=20°,则∠BCD= °.
11. 如图,直线l过正方形ABCD的顶点 B,点A,C 到直线l的距离分别是a 和b,且满足. |b﹣2|=0,则正方形ABCD的面积是 .
12. 如图,在矩形 ABCD 中,∠BOC = 120°,BD =12,点 P 是 AD 边上一动点,则 OP 的最小值为 .
13. 如图,在菱形ABCD中,点O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为3和4时,则阴影部分的面积为 .
14. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM
②无论点M运动到何处,都有
③在点 M的运动过程中,四边形 CEMD 可能成为菱形;
④无论点 M 运动到何处,∠CHM一定大于
以上结论正确的有 (把所有正确结论的序号都填上).
15. 如图,在菱形ABCD中,将对角线AC分别向两端延长到点E和F,使得 连接DE,DF,BE,BF.求证:四边形BEDF是菱形.
16. 如图,在矩形ABCD中,过对角线BD的中点O 作 BD的垂线EF,分别交AD,BC于点 E,F.
(1)求证:
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE 的周长.
17. 如图,已知四边形ABCD为正方形, ,点E为对角线AC上一动点,连接DE,过点E 作EF ,交BC于点F,以 DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG 是正方形.
(2)探究:的值是否为定值 若是,请求出这个定值;若不是,请说明理由.
知识点 2 多边形的镶嵌
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
18. 下列正多边形中,能够铺满地面的是 ( )
A.正方形 B.正五边形 C.正八边形 D.正十边形
19. 用三块正多边形的木板铺地,拼在一起的三块正多边形木板相交于一点且各边完全吻合,其中两块木板的边数都是5,则第三块木板的边数是 ( )
A.5 B.6 C.8 D.10
20. 在下列四组多边形的地板砖中:①正三角形与正方形;②正三角形与正十边形;③正方形与正六边形;④正方形与正八边形.将每组中的两种多边形结合,能密铺地面的是 ( )
A.①②③ B.①②④ C.③④ D.①④
21. 利用边长相等的正三角形和正六边形地砖能够铺满地板,若在每个顶点处有a块正三角形和b块正六边形(a>b>0),则a+b的值为 ( )
A.4 B.5 C.6 D.7
22. 用形状、大小完全相同的正三角形作平面镶嵌,则每个拼接点的周围有 个正三角形.
23. 在一个顶点处用边长相等的三个正多边形进行密铺,其中两个是正方形和正六边形,则另一个必须是正 边形.
24. 如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6 个正三角形,第2层包括6个正方形和18个正三角形,…,依此递推,则第6层中含有正三角形个数是 ,第n层中含有正三角形个数是 .
25. 在数学活动课上,研究用正多边形镶嵌平面.请解决以下问题:
(1)用一种正多边形镶嵌平面
例如,用6个全等的正三角形镶嵌平面,摆放方案如图所示:
若用m个全等的正n边形镶嵌平面,求出m,n应满足的关系式.
(2)用两种正多边形镶嵌平面
若这两种正多边形分别是边长相等的正三角形和正方形,请画出两种不同的摆放方案.
(3)用多种正多边形镶嵌平面
若镶嵌时每个顶点处的正多边形有n个,设这n个正多边形的边数分别为: 求出x1,x2,…,x 应满足的关系式.(用含n的式子表示)
第19 章基础复习(二)
1. B 2. A 3. C 4. C 5. B 6. D 7. D 8. B 9. B10. 70 11.5 12. 3 13. 3
14. ①②④
15. 证明:∵ 四边形ABCD是菱形,∴BC=CD,∠DCA=∠BCA,∴∠DCF=∠BCF.∵CF=CF,∴△CDF≌△CBF(SAS),∴DF=BF,∵AD∥BC,∴∠DAC=∠BCA,∴∠DAE=∠BCF,
∵AE=CF,DA=BC,∴△DAE≌△BCF(SAS),∴DE=BF,同理可证:△DCF≌△BAE(SAS),∴DF=BE,∴DF=BF=BE=DE,∴四边形BEDF是菱形.
16. (1)证明:∵ 四边形ABCD是矩形,∴AD∥BC,∴∠EDO=∠FBO.又∵EF⊥BD,∴∠EOD=∠FOB=90°,又∵O为BD中点,∴DO=BO,在△DOE和△BOF中, ∴△DOE≌△BOF(ASA).
(2)解:由(1)可得,ED∥BF,ED=BF,∴四边形BFDE是平行四边形.∵EF⊥BD,∴四边形BFDE是菱形,设AE=x,则BE=ED=8-x,在Rt△ABE中,根据勾股定理,得 即 解得 ∴四边形BFDE的周长为
17. (1)证明:如图,过点E作EM⊥BC于点M,EN⊥CD于点 N,则∠DNE=∠FME=90°,
∵ 四边形 ABCD 是正方形,
∴∠BCD=90°,∴∠MEN=90°,
∵ 点E是正方形ABCD对角线上的点,
∴EM=EN,
∵ 四边形 DEFG是矩形,∴∠DEF=90°,
∴∠DEN=∠FEM,在△DNE和△FME中,
∴△DEN≌△FEM(ASA),∴EF=ED,
∵ 四边形DEFG是矩形,∴矩形DEFG是正方形.
(2)解:CE+CG的值是定值,定值为6.理由如下:
∵ DE=DG,AD=DC,∠ADC=∠EDG=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
∴△ADE≌△CDG(SAS),∴AE=CG,
∴CE+CG的值是定值6.
18. A 19. D 20. D 21. B 22. 6 23. 12 24. 66 12n-6
25. 解:(1)∵正n边形的内角和为:180°(n-2),∴每个内角的度
数为: 由题意,得
即
(2)边长相等的正三角形和正方形镶嵌平面,有两种不同的摆放方案,如图所示:
(3)由题意,得
整理得
即
