沪科版数学八年级下册第 19 章 四边形 综合测试卷(含答案)
文档属性
| 名称 | 沪科版数学八年级下册第 19 章 四边形 综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 860.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 08:52:10 | ||
图片预览



文档简介
第 19 章综合测试卷
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 下列图形中具有稳定性的是 ( )
A.正六边形 B.五边形 C.平行四边形 D.钝角三角形
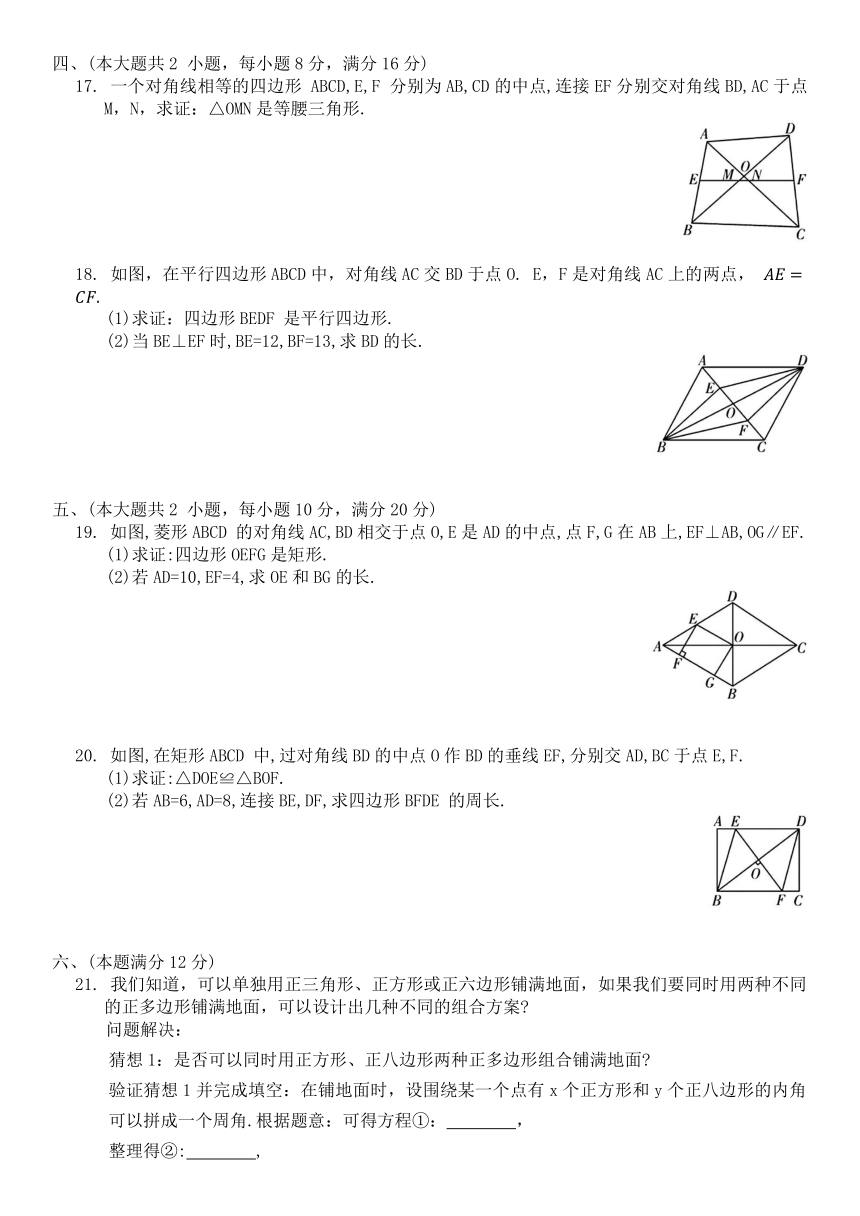
2. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作□BCDE,则∠E 的度数为 ( )
A.40° B.50° C.60° D.70°
3. 一个正多边形的外角与其相邻的内角之比为2:7,那么这个多边形的边数为 ( )
A.8 B.9 C.10 D.12
4. 正方形ABCD的一条对角线长为2,则正方形ABCD的周长为 ( )
A.4 B.8
5. 如图,在△ABC中,∠ACB=90°,AC=4,AB=5,D为AC上的动点,连接BD,以AD,BD为边作平行四边形ADBE,则DE长的最小值为 ( )
A.2 B.3 C.4 D.5
6. 只用一种正六边形地砖密铺地板,则能围绕在正六边形的一个顶点处的正六边形地砖有 ( )
A.3块 B.4块 C.5块 D.6块
7. 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若
AB=6cm,BC=8cm,则EF的长是 ( )
A.2. 2cm B.2. 3cm C.2.4 cm D.2. 5cm
8. 如图,在△ABC中,点D,E分别是边AB,AC的中点,点 F 是线段 DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是 ( )
A.2 B.3 C.4 D.5
9. 如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边CD,BC的中点,连接EF并延长与AB的延长线相交于点G,则EG= ( )
A.13 B.10 C.12 D.5
10. 如图,在边长为2 的正方形 EFGH中,M,N分别为EF 与GH 的中点,一个三角形ABC沿竖直方向向上平移,在运动的过程中,点A恒在直线MN上,当点A运动到线段MN的中点时,点E,F恰与AB,AC两边的中点重合,设点A到EF的距离为x,三角形ABC与正方形EFGH的公共部分的面积为y.则当 时,x的值为 ( )
A. 或 或 或
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 从八边形的一个顶点引出的对角线有 条.
12. 如图,在菱形ABCD中,∠B=50°,点E在CD上,若AE=AC,则∠BAE= °.
13. 如图,将正方形 OEFG 放在平面直角坐标系中,O是坐标原点,点E 的坐标为(2,3),则点 F 的坐标为 .
14. 如图,分别以 Rt△ABC的斜边 AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,分别连接DF,EF,DE,DE与AB 相交于点 G,若∠BAC=30°,下列四个结论:①EF⊥AC;②四边形ADFE 为平行四边形;③CE =2 AG;④△DBF≌△EFA.其中结论正确的是 .(填序号)
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,五边形ABCDE 的每个内角都相等,且∠1=∠2=∠3=∠4,求∠B和 的度数.
16. 如图,在△ABC中,点D 在边AC上,DB=BC,E是CD的中点,F是AB的中点,求证:
四、(本大题共2 小题,每小题8分,满分16分)
17. 一个对角线相等的四边形 ABCD,E,F 分别为AB,CD的中点,连接EF分别交对角线BD,AC于点M,N,求证:△OMN是等腰三角形.
18. 如图,在平行四边形ABCD中,对角线AC交BD于点O. E,F是对角线AC上的两点,
(1)求证:四边形BEDF 是平行四边形.
(2)当BE⊥EF时,BE=12,BF=13,求BD的长.
五、(本大题共2 小题,每小题10分,满分20分)
19. 如图,菱形ABCD 的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形.
(2)若AD=10,EF=4,求OE和BG的长.
20. 如图,在矩形ABCD 中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF.
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE 的周长.
六、(本题满分12分)
21. 我们知道,可以单独用正三角形、正方形或正六边形铺满地面,如果我们要同时用两种不同的正多边形铺满地面,可以设计出几种不同的组合方案
问题解决:
猜想1:是否可以同时用正方形、正八边形两种正多边形组合铺满地面
验证猜想1并完成填空:在铺地面时,设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意:可得方程①: ,
整理得②: ,
我们可以找到方程的正整数解为③: .
结论1:铺满地面时,在一个顶点周围围绕着④ 个正方形和⑤ 个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以铺满地面.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合铺满地面 若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
七、(本题满分12分)
22. 如图,在 ABCD中,对角线AC与BD相交于点O,点E,F 分别为OB,OD 的中点,延长AE 至G,使 EG=AE,连接CG.
(1)求证:△ABE≌△CDF.
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形 请说明理由.
八、(本题满分14分)
23. 如图,BD是正方形ABCD 的对角线,线段BC 在其所在的直线上平移,将平移得到的线段记为PQ,连接PA,过点Q作( 垂足为O,连接OA,OP.
(1)如图①所示,求证:
(2)如图②所示,PQ在 BC 的延长线上,如图③所示,PQ 在 BC 的反向延长线上,猜想线段AP,OA之间有怎样的数量关系 请直接写出你的猜想,不需证明.
第19章综合测试卷
1. D 2. D 3. B 4. D 5. B 6. A 7. D 8. B 9. B 10. A11. 5 12. 115 13. ( -1,5) 14. ①②③④
15. 解:∵ 五边形ABCDE的内角和等于 ,且每个内角都相等,
16. 证明:连接BE,
E是CD的中点,
∵ F是AB的中点,
17. 证明:取AD的中点Q,连接EQ,FQ,
∵E,F,Q分别为AB,CD,AD的中点,
∴∠QEF=∠OMN,∠QFE=∠ONM.
∵AC=BD,∴EQ=FQ,
∴∠QEF=∠QFE,
∴∠OMN=∠ONM,
∴OM=ON,∴△OMN是等腰三角形.
18. (1)证明:∵ 四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.∵OB=OD,
∴ 四边形 BEDF 是平行四边形.
(2)解:∵BE⊥EF,∴∠BEF=90°.
在 Rt△BEF中,
在 Rt△BEO中,
19. (1)证明:∵ 四边形 ABCD是菱形,∴OB=OD.∵E是AD的中点,∴OE是△ABD的中位线,∴OE∥FG.
∵OG∥EF,∴四边形OEFG是平行四边形.
∵EF⊥AB,∴∠EFG=90°,∴平行四边形OEFG是矩形.
(2)解:∵ 四边形ABCD是菱形,∴BD⊥AC,AB=AD=10,
∴∠AOD=90°.∵E是AD的中点, 由
(1)知,四边形OEFG是矩形,∴FG=OE=5.∵AE=5,EF=4,
20. (1)证明:∵ 四边形 ABCD 是矩形,∴AD∥BC,∴∠EDO =∠FBO.∵O为BD的中点,∴DO=BO.
在△DOE和△BOF中,
∴△DOE≌△BOF(ASA).
(2)解:由(1)可知,ED∥BF,ED=BF,∴四边形BFDE是平行四边形,又EF⊥BD,∴四边形BFDE是菱形.设AE=x,
∵AD=8,∴BE=ED=8﹣x.在Rt△ABE中,根据勾股定理可得, 即 解得
四边形 BFDE 的周长
21. 解:猜想1:根据题意,可得方程 整理,得 ,正整数解为:
故答案为:
结论1:铺满地面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角.故答案为1;2.
猜想2:能.理由如下:设围绕某一个点有x个正三角形和y个正六边形的内角可以拼成一个周角.
根据题意,可得方程 整理得
=6,正整数解为:
即可以同时用2个正三角形和2个正六边形或4个正三角形和1个正六边形组合铺满地面.
22. (1)证明:∵ 四边形ABCD是平行四边形,
∵点E,F分别为OB,OD的中点,
在 和 中,
(2)解:当 时,四边形EGCF是矩形.理由如下:
∵AC=2OC,AC=2AB,∴AB=OC=OA,
∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,
同理:CF⊥OD,∴AG∥CF,即 EG∥CF,
∵ △ABE≌△CDF,∴AE=CF,
∵EG=AE,∴EG=CF,∴四边形EGCF是平行四边形,
∵∠OEG=90°,∴四边形EGCF是矩形.
23. 证明:∵ 四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=
45°,∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,
∴OB=OQ,∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP=90°,∴△AOP是等腰直角三角形,
(2)解:①当PQ在BC的延长线上时,线段PA,OA之间的数量关系为: 理由如下:
∵ 四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,
∴OB=OQ,∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP =90°,∴△AOP是等腰直角三角形,.
②当PQ在BC的反向延长线上时,线段AP,OA之间的数量关系为: 理由如下:
∵ 四边形 ABCD是正方形,∴AB =BC,∠ABC=90°,∠ABD =∠CBD=45°,∴∠ABP=90°,∠OBQ=45°,∴∠ABO=135°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠OBQ=45°,
∴OB=OQ,∠PQO=135°,∴∠ABO=∠PQO,
∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP-∠POQ=90°,
∴∠BOP---∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,.
时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 下列图形中具有稳定性的是 ( )
A.正六边形 B.五边形 C.平行四边形 D.钝角三角形
2. 如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作□BCDE,则∠E 的度数为 ( )
A.40° B.50° C.60° D.70°
3. 一个正多边形的外角与其相邻的内角之比为2:7,那么这个多边形的边数为 ( )
A.8 B.9 C.10 D.12
4. 正方形ABCD的一条对角线长为2,则正方形ABCD的周长为 ( )
A.4 B.8
5. 如图,在△ABC中,∠ACB=90°,AC=4,AB=5,D为AC上的动点,连接BD,以AD,BD为边作平行四边形ADBE,则DE长的最小值为 ( )
A.2 B.3 C.4 D.5
6. 只用一种正六边形地砖密铺地板,则能围绕在正六边形的一个顶点处的正六边形地砖有 ( )
A.3块 B.4块 C.5块 D.6块
7. 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若
AB=6cm,BC=8cm,则EF的长是 ( )
A.2. 2cm B.2. 3cm C.2.4 cm D.2. 5cm
8. 如图,在△ABC中,点D,E分别是边AB,AC的中点,点 F 是线段 DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是 ( )
A.2 B.3 C.4 D.5
9. 如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边CD,BC的中点,连接EF并延长与AB的延长线相交于点G,则EG= ( )
A.13 B.10 C.12 D.5
10. 如图,在边长为2 的正方形 EFGH中,M,N分别为EF 与GH 的中点,一个三角形ABC沿竖直方向向上平移,在运动的过程中,点A恒在直线MN上,当点A运动到线段MN的中点时,点E,F恰与AB,AC两边的中点重合,设点A到EF的距离为x,三角形ABC与正方形EFGH的公共部分的面积为y.则当 时,x的值为 ( )
A. 或 或 或
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 从八边形的一个顶点引出的对角线有 条.
12. 如图,在菱形ABCD中,∠B=50°,点E在CD上,若AE=AC,则∠BAE= °.
13. 如图,将正方形 OEFG 放在平面直角坐标系中,O是坐标原点,点E 的坐标为(2,3),则点 F 的坐标为 .
14. 如图,分别以 Rt△ABC的斜边 AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,分别连接DF,EF,DE,DE与AB 相交于点 G,若∠BAC=30°,下列四个结论:①EF⊥AC;②四边形ADFE 为平行四边形;③CE =2 AG;④△DBF≌△EFA.其中结论正确的是 .(填序号)
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,五边形ABCDE 的每个内角都相等,且∠1=∠2=∠3=∠4,求∠B和 的度数.
16. 如图,在△ABC中,点D 在边AC上,DB=BC,E是CD的中点,F是AB的中点,求证:
四、(本大题共2 小题,每小题8分,满分16分)
17. 一个对角线相等的四边形 ABCD,E,F 分别为AB,CD的中点,连接EF分别交对角线BD,AC于点M,N,求证:△OMN是等腰三角形.
18. 如图,在平行四边形ABCD中,对角线AC交BD于点O. E,F是对角线AC上的两点,
(1)求证:四边形BEDF 是平行四边形.
(2)当BE⊥EF时,BE=12,BF=13,求BD的长.
五、(本大题共2 小题,每小题10分,满分20分)
19. 如图,菱形ABCD 的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形.
(2)若AD=10,EF=4,求OE和BG的长.
20. 如图,在矩形ABCD 中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF.
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE 的周长.
六、(本题满分12分)
21. 我们知道,可以单独用正三角形、正方形或正六边形铺满地面,如果我们要同时用两种不同的正多边形铺满地面,可以设计出几种不同的组合方案
问题解决:
猜想1:是否可以同时用正方形、正八边形两种正多边形组合铺满地面
验证猜想1并完成填空:在铺地面时,设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意:可得方程①: ,
整理得②: ,
我们可以找到方程的正整数解为③: .
结论1:铺满地面时,在一个顶点周围围绕着④ 个正方形和⑤ 个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以铺满地面.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合铺满地面 若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
七、(本题满分12分)
22. 如图,在 ABCD中,对角线AC与BD相交于点O,点E,F 分别为OB,OD 的中点,延长AE 至G,使 EG=AE,连接CG.
(1)求证:△ABE≌△CDF.
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形 请说明理由.
八、(本题满分14分)
23. 如图,BD是正方形ABCD 的对角线,线段BC 在其所在的直线上平移,将平移得到的线段记为PQ,连接PA,过点Q作( 垂足为O,连接OA,OP.
(1)如图①所示,求证:
(2)如图②所示,PQ在 BC 的延长线上,如图③所示,PQ 在 BC 的反向延长线上,猜想线段AP,OA之间有怎样的数量关系 请直接写出你的猜想,不需证明.
第19章综合测试卷
1. D 2. D 3. B 4. D 5. B 6. A 7. D 8. B 9. B 10. A11. 5 12. 115 13. ( -1,5) 14. ①②③④
15. 解:∵ 五边形ABCDE的内角和等于 ,且每个内角都相等,
16. 证明:连接BE,
E是CD的中点,
∵ F是AB的中点,
17. 证明:取AD的中点Q,连接EQ,FQ,
∵E,F,Q分别为AB,CD,AD的中点,
∴∠QEF=∠OMN,∠QFE=∠ONM.
∵AC=BD,∴EQ=FQ,
∴∠QEF=∠QFE,
∴∠OMN=∠ONM,
∴OM=ON,∴△OMN是等腰三角形.
18. (1)证明:∵ 四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.∵OB=OD,
∴ 四边形 BEDF 是平行四边形.
(2)解:∵BE⊥EF,∴∠BEF=90°.
在 Rt△BEF中,
在 Rt△BEO中,
19. (1)证明:∵ 四边形 ABCD是菱形,∴OB=OD.∵E是AD的中点,∴OE是△ABD的中位线,∴OE∥FG.
∵OG∥EF,∴四边形OEFG是平行四边形.
∵EF⊥AB,∴∠EFG=90°,∴平行四边形OEFG是矩形.
(2)解:∵ 四边形ABCD是菱形,∴BD⊥AC,AB=AD=10,
∴∠AOD=90°.∵E是AD的中点, 由
(1)知,四边形OEFG是矩形,∴FG=OE=5.∵AE=5,EF=4,
20. (1)证明:∵ 四边形 ABCD 是矩形,∴AD∥BC,∴∠EDO =∠FBO.∵O为BD的中点,∴DO=BO.
在△DOE和△BOF中,
∴△DOE≌△BOF(ASA).
(2)解:由(1)可知,ED∥BF,ED=BF,∴四边形BFDE是平行四边形,又EF⊥BD,∴四边形BFDE是菱形.设AE=x,
∵AD=8,∴BE=ED=8﹣x.在Rt△ABE中,根据勾股定理可得, 即 解得
四边形 BFDE 的周长
21. 解:猜想1:根据题意,可得方程 整理,得 ,正整数解为:
故答案为:
结论1:铺满地面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角.故答案为1;2.
猜想2:能.理由如下:设围绕某一个点有x个正三角形和y个正六边形的内角可以拼成一个周角.
根据题意,可得方程 整理得
=6,正整数解为:
即可以同时用2个正三角形和2个正六边形或4个正三角形和1个正六边形组合铺满地面.
22. (1)证明:∵ 四边形ABCD是平行四边形,
∵点E,F分别为OB,OD的中点,
在 和 中,
(2)解:当 时,四边形EGCF是矩形.理由如下:
∵AC=2OC,AC=2AB,∴AB=OC=OA,
∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,
同理:CF⊥OD,∴AG∥CF,即 EG∥CF,
∵ △ABE≌△CDF,∴AE=CF,
∵EG=AE,∴EG=CF,∴四边形EGCF是平行四边形,
∵∠OEG=90°,∴四边形EGCF是矩形.
23. 证明:∵ 四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=
45°,∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,
∴OB=OQ,∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP=90°,∴△AOP是等腰直角三角形,
(2)解:①当PQ在BC的延长线上时,线段PA,OA之间的数量关系为: 理由如下:
∵ 四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,
∴OB=OQ,∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP =90°,∴△AOP是等腰直角三角形,.
②当PQ在BC的反向延长线上时,线段AP,OA之间的数量关系为: 理由如下:
∵ 四边形 ABCD是正方形,∴AB =BC,∠ABC=90°,∠ABD =∠CBD=45°,∴∠ABP=90°,∠OBQ=45°,∴∠ABO=135°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠OBQ=45°,
∴OB=OQ,∠PQO=135°,∴∠ABO=∠PQO,
∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP-∠POQ=90°,
∴∠BOP---∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,.
