北师大版六年级上册数学整理复习 课件(共48张PPT)
文档属性
| 名称 | 北师大版六年级上册数学整理复习 课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览








文档简介
(共48张PPT)
第一单元 圆
圆的认识
小学 / 数学 / 北师大版 / 六年级上册
知识梳理:
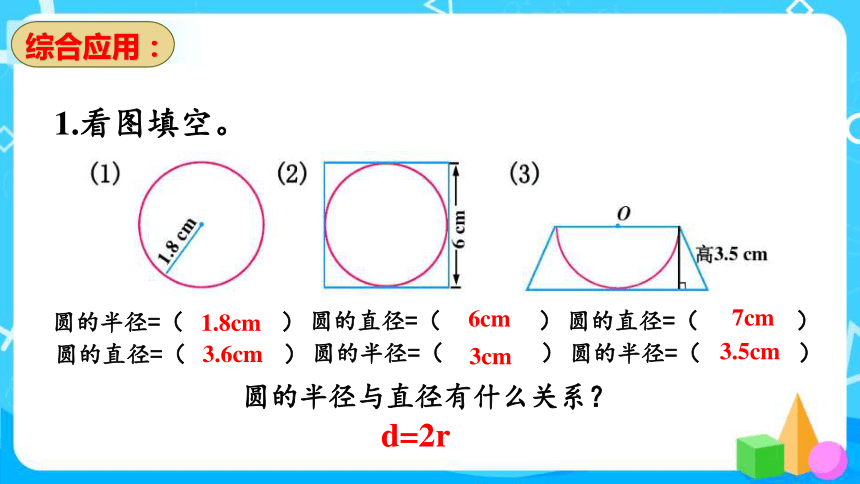
1.看图填空。
圆的半径=( )
圆的直径=( )
圆的直径=( )
圆的半径=( )
圆的直径=( )
圆的半径=( )
圆的半径与直径有什么关系?
d=2r
1.8cm
3.6cm
6cm
3cm
7cm
3.5cm
综合应用:
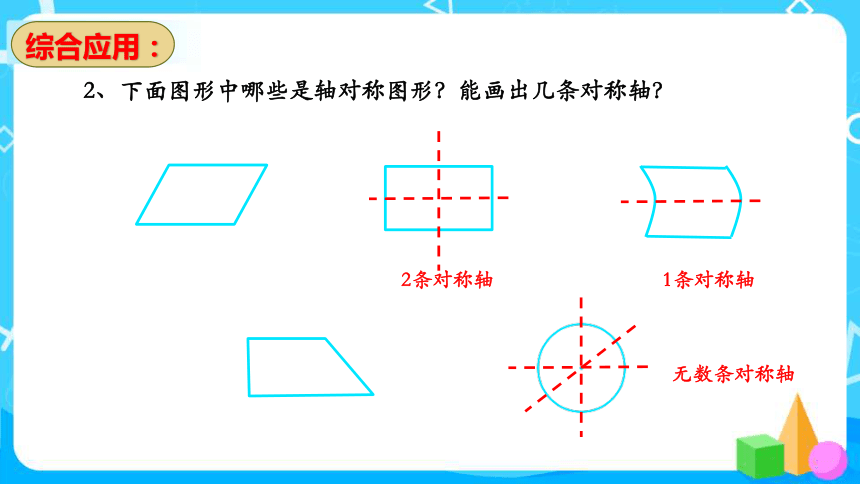
2、下面图形中哪些是轴对称图形?能画出几条对称轴?
2条对称轴
1条对称轴
无数条对称轴
综合应用:
根据下面的条件,求各圆的面积。
(1)3.14×4 =50.24(cm )
(2)3.14×(1.4÷2) =1.5386(dm )
(3)6.28÷3.14÷2=1(cm)
3.14×1 =3.14(cm )
(1)r=4cm (2)d=1.4dm (3)C=6.28cm
综合应用:
判断:
(1)两个半圆一定能拼成一个圆。 ( )
(2)半径是2厘米的圆,周长和面积相等。( )
(3)大圆的圆周率比小圆的圆周率大。 ( )
×
×
×
(4)半圆形纸片的周长就是圆周长的一半。( )
(5)圆心到圆上任意一点的距离都相等。 ( )
×
√
综合应用:
1. 圆中心的一点叫做( ),一般用字母( )表示。
2. 一个圆内有( )条直径,( )条半径。并且( )
条直径等于2 条半径。
3. 圆是( )图形,有( )条对称轴。
4. 把圆规的两脚分开,定好两脚间的距离作为( )。
5.周长相等的圆、正方形和长方形,( )的面积最大。
圆心
无数
无数
1
轴对称
半径
无数
圆
填空。
O
综合应用:
一根铁丝可以围成一个半径是3cm的圆,如果用它围成一个等边三角形,那么每边的长是多少厘米?
2×3.14×3=18.84cm
18.84÷3=6.28cm
答:每边的长是6.28cm。
银河广场有一个圆形喷水池,周长是43.96m,有一条3m宽的小路围着喷水池,这条小路的面积是多少?
小圆半径:
大圆半径:
43.96÷3.14÷2=7(m)
7+3=10(m)
小路面积:
3.14×(102-72)=160.14(m )
答:小路的面积是160.14m 。
综合应用:
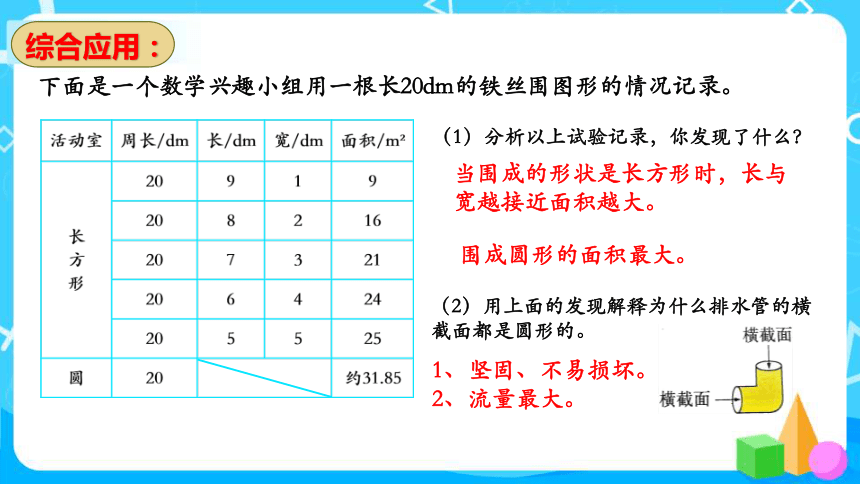
下面是一个数学兴趣小组用一根长20dm的铁丝围图形的情况记录。
(1)分析以上试验记录,你发现了什么?
(2)用上面的发现解释为什么排水管的横 截面都是圆形的。
当围成的形状是长方形时,长与宽越接近面积越大。
围成圆形的面积最大。
1、坚固、不易损坏。
2、流量最大。
综合应用:
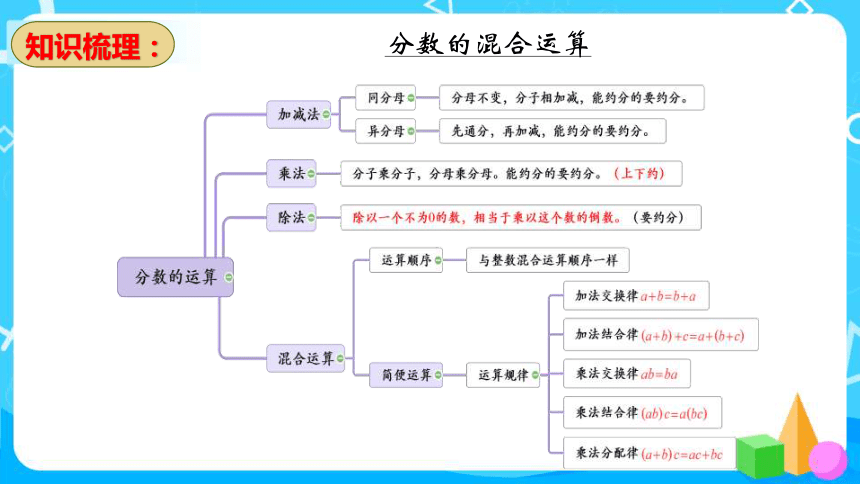
分数的混合运算
知识梳理:
解方程。
解:
5x-=2-
5x=1
5x÷5=1÷5
x=
解:
x=15
x÷=15÷
x=
解:
x÷=200÷
x=
综合应用:
计算下面各题。
=32×
=14
=×(
=
=
=
=×
=
=45×
=
=
=
=18
综合应用:
6、实验小学举行运动会,在50名运动员中,参加项目分布如下表。
7、在方格图中涂上颜色表示下面各百分数。
18%
50%
98%
综合应用:
地球的表面积约为5.1亿km ,海洋面积占整个地球表面积的71%。 海洋面积约是多少亿平方千米?(结果保留一位小数)
5.1×71%=5.1×0.71≈3.6(亿平方千米)
答:海洋面积约是3.6亿平方千米。
妙想有36枚邮票,奇思的邮票数是妙想的 ,笑笑的邮票数是 奇思的 ,笑笑有多少枚邮票?
答:笑笑有28枚邮票。
综合应用:
夹克比防寒服便宜 ,夹克是多少元?
答:夹克是160.8元。
笑笑买了一直圆珠笔和一支钢笔共用去24元,圆珠笔的单价是 钢笔的 。圆珠笔和钢笔的单价各是多少元?
4
答:圆珠笔的单价为4元, 钢笔的单价为20元。
综合应用:
用小正方体搭成一个立体图形,画出从正面、上面、左面看到的形状。
正面
上面
左面
两辆汽车从摄影师面前开过,摄影师依次拍摄了以下三幅照片。 请你用序号标出摄影师的拍摄顺序。
( )
( )
( )
①
②
③
综合应用:
1.计算下面各题。
×
=×
=×5×
=
×12
=×12+×12
=10+3
=13
÷54÷
=
=
综合应用:
÷×
=×
=
÷
= ÷
=
=
4+÷
=4+
=4
综合应用:
妙想有36枚邮票,奇思的邮票数是妙想的,笑笑的邮票数是奇思的,笑笑有多少张邮票?
36××=28(张)
答:笑笑有28张邮票。
综合应用:
夹克比防寒服便宜,夹克是多少元?
268×
=268×
=160.8(元)
答:夹克是160.8元。
综合应用:
笑笑买了一支圆珠笔和一支钢笔共用去24元,圆珠笔的单价是钢笔的。圆珠笔和钢笔的单价各是多少元?
解:设钢笔的单价各是x元。
x + x=24
x=24
x=20
24-20=4(元)
答:圆珠笔的单价是4元,钢笔的单价是20元。
综合应用:
小林看一本180页的童话书,已经看了,还剩多少页没有看
180-180×
=180-120
=60(页)
答:还剩60页没有看。
综合应用:
一件上衣78元,一条裤子比一件上衣便宜。这条裤子多少元
78×
= 78×
=65(元)
答:这条裤子65元。
综合应用:
百分数的认识
小数、分数化成百分数
用方程解决有关百分数问题
百分数化成小数、分数
课堂总结:
从三个不同的方向观察物体
不同位置观察物体的范围
不同位置观察物体的相对位置
观察物体
课堂总结:
1.百分数的认识
表示一个数是另一个数的百分之几的数叫作百分数。百分数也叫百分比或百分率。
百分数通常不写成分母是100的分数形式,而是先写分子,再在分子后面加上“%”,读作百分之几。
课堂总结:
发芽率
出粉率
成活率
出油率
命中率
发芽种子数
种子总数
发芽率=
×100%
面粉质量
小麦质量
出粉率=
×100%
命中次数
总次数
命中率=
×100%
成活种子数量
种子总数量
成活率=
×100%
油的质量
总质量
出油率=
×100%
2.小数、分数化成百分数
知识梳理:
2.小数、分数化成百分数
①先把小数化成分母是100的分数,再改写成百分数;②把小数点向右移动两位,同时在后面添上百分号即可。
①先把分数化成分母是100的分数,再改写成百分数;②把分数化成小数后,再改写成百分数。(除不尽时,百分号前保留一位小数)
知识梳理:
3.百分数化成小数、分数
百分数化成小数:把百分号去掉,同时把小数点向左移动两位,位数不够时,用“0”补足。
百分数化成分数:先把百分数改写成分母是100的分数,然后进行约分。
知识梳理:
4.解决有关百分数问题
先确定
单位“1”;
找到数量关系;
列出方程并求解。
“已知一个数的百分之几是多少,求这个数”问题:
知识梳理:
4.解决有关百分数问题
单位“1”×对应分率=部分量
部分量÷对应分率=单位“1”
部分量÷单位“1”×100%=对应分率
知识梳理:
5.观察物体
1.根据从一个方向看到的图形可以摆出多种几何体。根据从三个方向看到的图形所搭成的几何体是确定的,摆法唯一。
2.不同位置观察到物体的范围不同。
3.不同位置观察到物体的形状不同。
知识梳理:
1.填空题。
(1)500克的70%是( )克,8千克是5千克的( )%。
(2)一个数的30%是24,这个数的90%是( )。
(3)27.65%读作( );百分之八十三写作( )。
(4)李爷爷家的果园里新栽了300棵梨树,成活了270棵,这些梨树的成活率是( )。
350
160
72
百分之二十七点六五
83%
90%
综合应用:
2.判断题。
(1)丽丽买来一个10%千克的西瓜。( )
(2)0.5%的分子不是整数,所以0.5%不是百分数。( )
(3)5千克的10%与10千克的5%相等。( )
(4)10克白糖放到100克水中,糖水的含糖率是10%。( )
×
×
√
×
综合应用:
3.选择题。
(1)五1班有40名学生,今天有1人请假,今天的出勤率是( )。
A. 2.5% B. 97.5% C. 99%
(2)今年比去年增收20%,就是说今年收获的是去年收获的( )。
A. 20% B. 80% C. 120%
(3)甲数是乙数的80%,丙数是甲数的80%,三个数中 ( )最大。
A. 甲数 B. 乙数 C. 丙数
B
C
B
综合应用:
4.完成下表。
分数
小数 0.25
百分数 87.5%
0.75
75%
25%
0.6
0.875
60%
综合应用:
5.在方格图中图上颜色表示下面各百分数。
18%
50%
98%
综合应用:
6. 芳芳能看到甲楼上的 A 点吗 能看到甲楼上的 B 点吗 作图说明。
芳芳能看到甲楼上的 A 点,不能看到甲楼上的 B 点。
综合应用:
7.实验小学举行运动会,在50名运动员中,参加项目分布如下表。
项目 田径 球类 游泳
人数 19 18 13
占运动员总人数的百分之几
各类项目人数÷运动员总人数=所占百分比
38%
36%
26%
综合应用:
一件上衣按七五折出售的价格是150元,这件上衣的原价是多少元?
解:这件上衣的原价是x元。
75% x =150
x =150÷75%
x =200
答:这件上衣的原价是200元。
原价的75%
综合应用:
18.84
28.26
2.5
12cm
2cm
0.2826
综合应用:
5
7
综合应用:
综合应用:
综合应用:
综合应用:
综合应用:
综合应用:
综合应用:
第一单元 圆
圆的认识
小学 / 数学 / 北师大版 / 六年级上册
知识梳理:
1.看图填空。
圆的半径=( )
圆的直径=( )
圆的直径=( )
圆的半径=( )
圆的直径=( )
圆的半径=( )
圆的半径与直径有什么关系?
d=2r
1.8cm
3.6cm
6cm
3cm
7cm
3.5cm
综合应用:
2、下面图形中哪些是轴对称图形?能画出几条对称轴?
2条对称轴
1条对称轴
无数条对称轴
综合应用:
根据下面的条件,求各圆的面积。
(1)3.14×4 =50.24(cm )
(2)3.14×(1.4÷2) =1.5386(dm )
(3)6.28÷3.14÷2=1(cm)
3.14×1 =3.14(cm )
(1)r=4cm (2)d=1.4dm (3)C=6.28cm
综合应用:
判断:
(1)两个半圆一定能拼成一个圆。 ( )
(2)半径是2厘米的圆,周长和面积相等。( )
(3)大圆的圆周率比小圆的圆周率大。 ( )
×
×
×
(4)半圆形纸片的周长就是圆周长的一半。( )
(5)圆心到圆上任意一点的距离都相等。 ( )
×
√
综合应用:
1. 圆中心的一点叫做( ),一般用字母( )表示。
2. 一个圆内有( )条直径,( )条半径。并且( )
条直径等于2 条半径。
3. 圆是( )图形,有( )条对称轴。
4. 把圆规的两脚分开,定好两脚间的距离作为( )。
5.周长相等的圆、正方形和长方形,( )的面积最大。
圆心
无数
无数
1
轴对称
半径
无数
圆
填空。
O
综合应用:
一根铁丝可以围成一个半径是3cm的圆,如果用它围成一个等边三角形,那么每边的长是多少厘米?
2×3.14×3=18.84cm
18.84÷3=6.28cm
答:每边的长是6.28cm。
银河广场有一个圆形喷水池,周长是43.96m,有一条3m宽的小路围着喷水池,这条小路的面积是多少?
小圆半径:
大圆半径:
43.96÷3.14÷2=7(m)
7+3=10(m)
小路面积:
3.14×(102-72)=160.14(m )
答:小路的面积是160.14m 。
综合应用:
下面是一个数学兴趣小组用一根长20dm的铁丝围图形的情况记录。
(1)分析以上试验记录,你发现了什么?
(2)用上面的发现解释为什么排水管的横 截面都是圆形的。
当围成的形状是长方形时,长与宽越接近面积越大。
围成圆形的面积最大。
1、坚固、不易损坏。
2、流量最大。
综合应用:
分数的混合运算
知识梳理:
解方程。
解:
5x-=2-
5x=1
5x÷5=1÷5
x=
解:
x=15
x÷=15÷
x=
解:
x÷=200÷
x=
综合应用:
计算下面各题。
=32×
=14
=×(
=
=
=
=×
=
=45×
=
=
=
=18
综合应用:
6、实验小学举行运动会,在50名运动员中,参加项目分布如下表。
7、在方格图中涂上颜色表示下面各百分数。
18%
50%
98%
综合应用:
地球的表面积约为5.1亿km ,海洋面积占整个地球表面积的71%。 海洋面积约是多少亿平方千米?(结果保留一位小数)
5.1×71%=5.1×0.71≈3.6(亿平方千米)
答:海洋面积约是3.6亿平方千米。
妙想有36枚邮票,奇思的邮票数是妙想的 ,笑笑的邮票数是 奇思的 ,笑笑有多少枚邮票?
答:笑笑有28枚邮票。
综合应用:
夹克比防寒服便宜 ,夹克是多少元?
答:夹克是160.8元。
笑笑买了一直圆珠笔和一支钢笔共用去24元,圆珠笔的单价是 钢笔的 。圆珠笔和钢笔的单价各是多少元?
4
答:圆珠笔的单价为4元, 钢笔的单价为20元。
综合应用:
用小正方体搭成一个立体图形,画出从正面、上面、左面看到的形状。
正面
上面
左面
两辆汽车从摄影师面前开过,摄影师依次拍摄了以下三幅照片。 请你用序号标出摄影师的拍摄顺序。
( )
( )
( )
①
②
③
综合应用:
1.计算下面各题。
×
=×
=×5×
=
×12
=×12+×12
=10+3
=13
÷54÷
=
=
综合应用:
÷×
=×
=
÷
= ÷
=
=
4+÷
=4+
=4
综合应用:
妙想有36枚邮票,奇思的邮票数是妙想的,笑笑的邮票数是奇思的,笑笑有多少张邮票?
36××=28(张)
答:笑笑有28张邮票。
综合应用:
夹克比防寒服便宜,夹克是多少元?
268×
=268×
=160.8(元)
答:夹克是160.8元。
综合应用:
笑笑买了一支圆珠笔和一支钢笔共用去24元,圆珠笔的单价是钢笔的。圆珠笔和钢笔的单价各是多少元?
解:设钢笔的单价各是x元。
x + x=24
x=24
x=20
24-20=4(元)
答:圆珠笔的单价是4元,钢笔的单价是20元。
综合应用:
小林看一本180页的童话书,已经看了,还剩多少页没有看
180-180×
=180-120
=60(页)
答:还剩60页没有看。
综合应用:
一件上衣78元,一条裤子比一件上衣便宜。这条裤子多少元
78×
= 78×
=65(元)
答:这条裤子65元。
综合应用:
百分数的认识
小数、分数化成百分数
用方程解决有关百分数问题
百分数化成小数、分数
课堂总结:
从三个不同的方向观察物体
不同位置观察物体的范围
不同位置观察物体的相对位置
观察物体
课堂总结:
1.百分数的认识
表示一个数是另一个数的百分之几的数叫作百分数。百分数也叫百分比或百分率。
百分数通常不写成分母是100的分数形式,而是先写分子,再在分子后面加上“%”,读作百分之几。
课堂总结:
发芽率
出粉率
成活率
出油率
命中率
发芽种子数
种子总数
发芽率=
×100%
面粉质量
小麦质量
出粉率=
×100%
命中次数
总次数
命中率=
×100%
成活种子数量
种子总数量
成活率=
×100%
油的质量
总质量
出油率=
×100%
2.小数、分数化成百分数
知识梳理:
2.小数、分数化成百分数
①先把小数化成分母是100的分数,再改写成百分数;②把小数点向右移动两位,同时在后面添上百分号即可。
①先把分数化成分母是100的分数,再改写成百分数;②把分数化成小数后,再改写成百分数。(除不尽时,百分号前保留一位小数)
知识梳理:
3.百分数化成小数、分数
百分数化成小数:把百分号去掉,同时把小数点向左移动两位,位数不够时,用“0”补足。
百分数化成分数:先把百分数改写成分母是100的分数,然后进行约分。
知识梳理:
4.解决有关百分数问题
先确定
单位“1”;
找到数量关系;
列出方程并求解。
“已知一个数的百分之几是多少,求这个数”问题:
知识梳理:
4.解决有关百分数问题
单位“1”×对应分率=部分量
部分量÷对应分率=单位“1”
部分量÷单位“1”×100%=对应分率
知识梳理:
5.观察物体
1.根据从一个方向看到的图形可以摆出多种几何体。根据从三个方向看到的图形所搭成的几何体是确定的,摆法唯一。
2.不同位置观察到物体的范围不同。
3.不同位置观察到物体的形状不同。
知识梳理:
1.填空题。
(1)500克的70%是( )克,8千克是5千克的( )%。
(2)一个数的30%是24,这个数的90%是( )。
(3)27.65%读作( );百分之八十三写作( )。
(4)李爷爷家的果园里新栽了300棵梨树,成活了270棵,这些梨树的成活率是( )。
350
160
72
百分之二十七点六五
83%
90%
综合应用:
2.判断题。
(1)丽丽买来一个10%千克的西瓜。( )
(2)0.5%的分子不是整数,所以0.5%不是百分数。( )
(3)5千克的10%与10千克的5%相等。( )
(4)10克白糖放到100克水中,糖水的含糖率是10%。( )
×
×
√
×
综合应用:
3.选择题。
(1)五1班有40名学生,今天有1人请假,今天的出勤率是( )。
A. 2.5% B. 97.5% C. 99%
(2)今年比去年增收20%,就是说今年收获的是去年收获的( )。
A. 20% B. 80% C. 120%
(3)甲数是乙数的80%,丙数是甲数的80%,三个数中 ( )最大。
A. 甲数 B. 乙数 C. 丙数
B
C
B
综合应用:
4.完成下表。
分数
小数 0.25
百分数 87.5%
0.75
75%
25%
0.6
0.875
60%
综合应用:
5.在方格图中图上颜色表示下面各百分数。
18%
50%
98%
综合应用:
6. 芳芳能看到甲楼上的 A 点吗 能看到甲楼上的 B 点吗 作图说明。
芳芳能看到甲楼上的 A 点,不能看到甲楼上的 B 点。
综合应用:
7.实验小学举行运动会,在50名运动员中,参加项目分布如下表。
项目 田径 球类 游泳
人数 19 18 13
占运动员总人数的百分之几
各类项目人数÷运动员总人数=所占百分比
38%
36%
26%
综合应用:
一件上衣按七五折出售的价格是150元,这件上衣的原价是多少元?
解:这件上衣的原价是x元。
75% x =150
x =150÷75%
x =200
答:这件上衣的原价是200元。
原价的75%
综合应用:
18.84
28.26
2.5
12cm
2cm
0.2826
综合应用:
5
7
综合应用:
综合应用:
综合应用:
综合应用:
综合应用:
综合应用:
综合应用:
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
