人教版数学六年级上册第五单元测试卷(含答案)
文档属性
| 名称 | 人教版数学六年级上册第五单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 10:41:31 | ||
图片预览




文档简介
人教版数学六年级上册第五单元测试卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
一、选择题
1.如图,甲图和乙图中的两个圆的半径都是4厘米,两图中涂色部分的面积相比,( )。
A.甲大 B.乙大 C.相等
2.两个圆的面积不相等,原因是它们( )。
A.圆心的位置不同 B.圆周率不同 C.直径不相等 D.画法不同
3.两个圆的半径分别是6cm、4cm,大圆和小圆的面积比是( )。
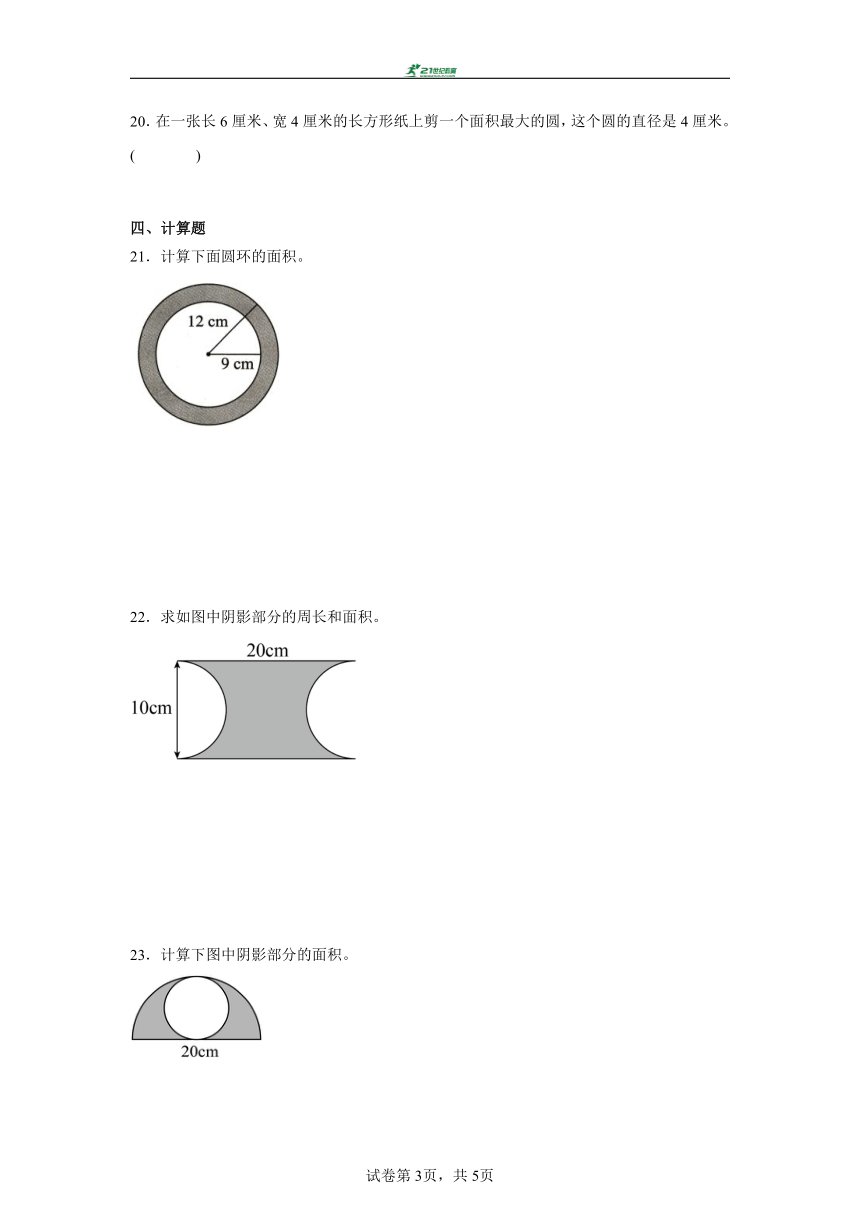
A.2∶3 B.9∶4 C.3∶2
4.一个圆环,它的外圆直径是内圆直径的两倍,则这个圆环的面积为( )。
A.比内圆面积大 B.比内圆面积小 C.与内圆面积一样大 D.无法判断
5.如果小圆的直径等于大圆的半径,那么大圆的面积是小圆面积的( )。
A. B.2倍 C.4倍
二、填空题
6.一只挂钟的时针长7厘米,转动一周,针尖走过的路程是( )厘米.
7.如图中4个圆的大小相同,则阴影部分表示的扇形面积最大的是( ),面积最小的是( )。
8.圆的半径一般用( )表示,直径用( )表示,面积公式用( )表示,周长公式用( )表示.
9.在一个长6厘米,宽4厘米的长方形内画一个最大的圆,这个圆的面积是( )平方厘米。
10.白居易的《府西池》中“柳元气力枝先动,池有波纹冰尽开”,描述了雨点打在水面上荡开层层波纹的情景。已知一个长方形水池的长是8m,宽是6m,当波纹到池边时,所形成的最大整圆的周长是( )m,面积是( )m2。
11.小刚量得一个树干的横截面的周长是125.6厘米,树干的横截面近似圆形,它的横截面大约是( )平方厘米。
12.李师傅想把3根横截面直径都是10cm的圆木用铁丝紧紧地捆绑在一起(如图),捆一圈(接头不计)至少需要铁丝( )cm,铁丝围成的图形面积是( )cm2。
13.一个圆的直径是12cm,它的周长是( )cm,面积是( )。
14.一个圆的周长扩大5倍,直径扩大( )倍,面积扩大( )。
15.下图中圆的周长是18.84dm,则圆的面积是( )dm2,正方形的面积是( )dm2。
三、判断题
16.半径越大,圆的面积越大. ( )
17.半圆的面积和周长分别是同直径圆面积和周长的一半。( )
18.一个圆的半径从4m增加到6m,这个圆的面积增加了6.28m2。( )
19.一个圆的半径扩大到原来的2倍,它的面积也扩大到原来的2倍。( )
20.在一张长6厘米、宽4厘米的长方形纸上剪一个面积最大的圆,这个圆的直径是4厘米。( )
四、计算题
21.计算下面圆环的面积。
22.求如图中阴影部分的周长和面积。
23.计算下图中阴影部分的面积。
五、解答题
24.沿着直径是8米的圆形水池周围铺一条1米宽的石子路,石子路占地面积是多少平方米?
25.用一根长30分米的绳子绕一根圆柱形柱子三圈后还多1.74分米,这根圆柱形柱子的直径是多少分米?
26.一个圆形音乐喷泉的周长是502.4米,喷泉外围修了一条宽4米的小路作为观赏区,观赏区外围的周长是多少米?
27.如图所示,一个运动场的两边是相同的半圆,中间是长方形,这个运动场的占地面积是多少平方米?
28.用20米长的铁条做直径是60厘米的圆形铁环,最多可以做多少个?
29.为进一步推进新农村建设,幸福新村新建了一个周长为94.2米的圆形花坛。为了便于游客观赏,村委会决定在花坛的四周铺一条环形的石子路,石子路宽1米。如果每平方米小路需要80千克石子,那么修这条路一共需要多少千克石子?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 B C B A C
1.B
【分析】甲图是外方内圆,圆的直径等于正方形边长;乙图是外圆内方,圆的直径等于正方形对角线,据此分别计算甲、乙的涂色部分面积,再比较大小解答。
【详解】甲图:正方形边长4×2=8(厘米)
涂色部分的面积是:82-3.14×42
=64-50.24
=13.76(平方厘米)
乙图:正方形对角线长是4×2=8(厘米)
涂色部分的面积是:3.14×42-8×4÷2×2
=50.24-32
=18.24(平方厘米)
因为18.24>13.76,所以乙图中涂色部分的面积大。
故答案为:B
【点睛】本题考查外方内圆和外圆内方图形的相关计算,解题关键是找到正方形与圆的半径的关联。
2.C
【分析】圆心决定圆的位置,半径决定圆的大小,同圆或等圆中直径是半径的2倍。据此解答。
【详解】A.圆心只决定圆的位置,不能决定圆的面积大小,原因错误;
B.所有圆的圆周率都相同,原因错误;
C.两个圆的直径不相等,则它们的半径不相等,那么两个圆的面积就不相等,原因正确;
D.圆的画法不同,不能决定圆的面积大小,原因错误。
故答案为:C
3.B
【分析】根据圆的面积公式:面积=π×半径2,代入数据,求出圆的面积,再根据比的意义,用大圆面积∶小圆面积,即可解答。
【详解】(π×62)∶(π×42)
=(36π)∶(16π)
=(36π÷4π)∶(16π÷4π)
=9∶4
两个圆的半径分别是6cm、4cm,大圆和小圆的面积比是9∶4。
故答案为:B
4.A
【分析】圆的直径÷2=半径,如果圆环的外圆直径是内圆直径的两倍,则它的外圆半径也是内圆半径的两倍。圆环的面积=外圆面积-内圆面积,设这个圆环的内圆半径是r,则外圆半径是2r,根据圆的面积公式S=πr2,分别求出内圆和外圆的面积,再把它们相减即可求出圆环的面积。据此解答。
【详解】设这个圆环的内圆半径是r,则外圆半径是2r。
外圆面积:π×(2r)2
=π×4r2
=4πr2
内圆面积:πr2
圆环面积:4πr2-πr2=3πr2
3πr2>πr2,则这个圆环的面积比内圆面积大。
故答案为:A
5.C
【分析】为了方便理解和计算,用设数法,设小圆的直径、大圆的半径都是2。根据圆的面积公式:S=πr2,分别计算出小圆和大圆的面积,再用大圆面积除以小圆的面积即可。
【详解】设小圆的直径、大圆的半径都是2。
小圆的半径是:2÷2=1
小圆的面积:π×12=π
大圆的面积:π×22=4π
大圆的面积是小圆面积的:
故答案为:C
【点睛】掌握用设数法解决问题的方法。
6.43.96
【解析】略
7. ④ ①
【分析】在同圆或等圆中,扇形的圆心角越大,扇形的面积越大。据此解答。
【详解】
从图中可知:>>>
则阴影部分表示的扇形面积最大的是④,面积最小的是①。
8. R d s=πr c=πd
【详解】略
9.12.56
【详解】长方形内最大的圆的直径等于长方形的最短边4厘米,据此利用圆的面积公式计算即可
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
10. 18.84 28.26
【详解】根据题意可知,在这个长方形水池中波纹所形成最大圆的直径就是这个长方形水池的宽即为是6米,根据圆的周长公式:C=πd,圆的面积公式;S=πr2,把数据代入公式解答。
【解答】3.14×6=18.84(m)
3.14×(6÷2)2
=3.14×32
=3.14×9
=28.26(m2)
则所形成的最大整圆的周长是18.84m,面积是28.26m2。
11.1256
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出树干的半径,再根据圆的面积公式:面积=π×半径2,代入数据,即可求出横截面的面积。
【详解】125.6÷3.14÷2
=40÷2
=20(厘米)
3.14×202
=3.14×400
=1256(平方厘米)
小刚量得一个树干的横截面的周长是125.6厘米,树干的横截面近似圆形,它的横截面大约是1256平方厘米。
12. 71.4 278.5
【分析】求捆一圈至少需要铁丝的长度,就是求图形的周长;图形最左边和最右边各有一个直径为10cm的半圆,可以组成一个圆;图形上面、下面的铁丝长度各相当于2条直径,所以铁丝的总长度=圆的周长+4条直径的长度,根据圆的周长公式C=πd,代入数据计算求解。
铁丝围成的图形面积=圆的面积+长方形的面积,其中圆的半径是(10÷2)cm,长方形的长是(10×2)cm,宽是10cm;根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算求解。
【详解】3.14×10+10×4
=31.4+40
=71.4(cm)
3.14×(10÷2)2+(10×2)×10
=3.14×52+20×10
=3.14×25+200
=78.5+200
=278.5(cm2)
捆一圈(接头不计)至少需要铁丝71.4cm,铁丝围成的图形面积是278.5cm2。
13. 37.68 113.04
【分析】圆的周长=,圆的面积=,据此解答即可。
【详解】3.14×12=37.68(厘米)
3.14×(12÷2)2
=3.14×36
=113.04(平方厘米)
【点睛】本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积计算公式。
14. 5 25
【详解】略
15. 28.26 18
【分析】将圆的周长除以3.14再除以2,求出圆的半径,从而根据圆面积S=πr2列式求出圆的面积;
将正方形沿着一条对角线一分为二,每个小三角形的底是圆的直径,高是圆的半径,根据三角形面积=底×高÷2,求出一个三角形的面积。将一个三角形的面积乘2,即可求出正方形的面积。
【详解】18.84÷3.14÷2=3(dm)
3.14×32=28.26(dm2)
(3×2)×3÷2×2
=6×3÷2×2
=18(dm2)
所以,圆的面积是28.26dm2,正方形的面积是18dm2。
【点睛】本题考查了圆的周长和面积、三角形的面积,熟记公式并灵活运用是解题的关键。
16.√
【解析】略
17.×
【分析】半圆的面积等于同直径圆面积的一半,半圆的周长等于同直径圆周长的一半加上直径。据此判断。
【详解】由分析可知,半圆的面积等于同直径圆面积的一半,而半圆的周长不等于同直径圆周长的一半。
所以原题说法错误。
故答案为:×
18.×
【分析】增加的部分是个圆环,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】3.14×(62-42)
=3.14×(36-16)
=3.14×20
=62.8(m2)
一个圆的半径从4m增加到6m,这个圆的面积增加了62.8m2,原说法错误。
故答案为:×
19.×
【分析】此题考查了积的变化规律在圆的面积公式中的灵活应用,这里可得结论:圆的半径扩大n倍,则这个圆的面积就扩大n的平方倍。圆的面积=π×r×r,其中π是一个定值,根据积的变化规律:一个因数不变,另一个因数扩大几倍,积就扩大几倍,即可解答。
【详解】圆的面积=π×r×r,r扩大2倍,则圆的面积就扩大:2×2=4倍,所以原题说法错误。
故答案为:×
20.√
【分析】在长方形纸上剪一个面积最大的圆,圆的直径=长方形的宽,据此分析。
【详解】在一张长6厘米、宽4厘米的长方形纸上剪一个面积最大的圆,这个圆的直径是4厘米,说法正确。
故答案为:√
21.197.82cm2
【分析】从图中可知,大圆的半径R是12cm,小圆的半径r是9cm;根据圆环的面积公式S环=π(R2-r2),代入数据计算,求出圆环的面积。
【详解】3.14×(122-92)
=3.14×(144-81)
=3.14×63
=197.82(cm2)
圆环的面积是197.82cm2。
22.阴影部分的周长是71.4厘米,面积是121.5平方厘米
【分析】通过观察可知,阴影部分的周长等于圆的周长加上2条20厘米的线段的长,面积等于长方形面积减去圆的面积,圆的直径相当于长方形的宽,也就是10厘米,根据长方形的面积=长×宽、圆周长公式:C=πd、圆面积公式:S=πr2,代入数据计算即可。
【详解】3.14×10+20×2
=31.4+40
=71.4(厘米)
20×10-3.14×(10÷2)2
=20×10-3.14×52
=200-3.14×25
=200-78.5
=121.5(平方厘米)
阴影部分的周长是71.4厘米,面积是121.5平方厘米。
23.78.5平方厘米
【分析】由图可知,外部大圆直径是20厘米,内部小圆是以大圆的半径为直径。阴影部分的面积等于直径是20厘米的半圆面积减去直径是10厘米的整圆面积,据此解答。
【详解】3.14×(20÷2)2÷2-3.14×(20÷2÷2)2
=3.14×102÷2-3.14×52
=3.14×100÷2-3.14×25
=157-78.5
=78.5(平方厘米)
阴影部分面积是78.5平方厘米。
24.28.26平方米
【分析】求石子路的占地面积就是求圆环的面积,根据圆环的面积公式:S=-,据此进行计算即可。
【详解】8÷2=4(米)
4+1=5(米)
3.14×-3.14×42
=3.14×25-3.14×16
=3.14×(25-16)
=3.14×9
=28.26(平方米)
答:石子路占地面积是28.26平方米。
25.3分米
【分析】用这个绳子的长度减去剩余的1.74分米,求出这个柱子底面周长的3倍,再除以3求出柱子的底面周长,然后根据圆的周长公式:C=πd,那么d=C÷π,把数据代入公式解答。
【详解】(30-1.74)÷3÷3.14
=28.26÷3÷3.14
=9.42÷3.14
=3(分米)
答:这个柱子的直径是3分米。
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
26.527.52米
【分析】一个圆形音乐喷泉的周长是502.4米,根据圆的周长=,得出圆的半径是80米,喷泉外围修了一条宽4米的小路作为观赏区,则外面的圆是一个半径是84米,根据圆的周长公式求出圆的周长。
【详解】502.4÷3.14=160(米)
160÷2=80(米)
(80+4)×2×3.14
=84×2×3.14
=527.52(米)
答:观赏区外围的周长是527.52米。
27.1314平方米
【分析】根据图可知,左右两边是两个半圆形,则相当于一个直径是20米的圆,中间是长方形,长是50米,宽是20米,根据圆的面积公式:,长方形的面积=长×宽,把数代入求出这两部分的面积,再相加即可。
【详解】
=3.14×100+1000
=314+1000
=1314(平方米)
答:这个运动场的面积是1314平方米。
28.10个
【分析】根据圆的周长公式:周长=π×直径,代入数据,求出圆形铁环的周长,再用铁条的长度÷圆形铁环的周长,最后无论剩下多少厘米铁条,只要不够一个圆形铁环就无法制作一个铁环,结果用“去尾法”取整数,据此解答,注意单位名数的统一。
【详解】20米=2000厘米
2000÷(3.14×60)
=2000÷188.4
≈10(个)
答:最大可以做10个。
29.7787.2千克
【分析】根据圆周长公式:C=2πr,代入数据即可求出花坛的半径,再加上1米,即可求出石子路外圆的半径,然后根据圆环的面积公式:S=π(R2-r2),求出小路的面积即可;再乘80千克,即可求出石子的总千克数。
【详解】94.2÷3.14÷2
=30÷2
=15(米)
15+1=16(米)
3.14×162-3.14×152
=3.14×256-3.14×225
=803.84-706.5
=97.34(平方米)
97.34×80=7787.2(千克)
答:修这条路一共需要7787.2千克石子。
答案第11页,共22页
答案第11页,共22页
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
一、选择题
1.如图,甲图和乙图中的两个圆的半径都是4厘米,两图中涂色部分的面积相比,( )。
A.甲大 B.乙大 C.相等
2.两个圆的面积不相等,原因是它们( )。
A.圆心的位置不同 B.圆周率不同 C.直径不相等 D.画法不同
3.两个圆的半径分别是6cm、4cm,大圆和小圆的面积比是( )。
A.2∶3 B.9∶4 C.3∶2
4.一个圆环,它的外圆直径是内圆直径的两倍,则这个圆环的面积为( )。
A.比内圆面积大 B.比内圆面积小 C.与内圆面积一样大 D.无法判断
5.如果小圆的直径等于大圆的半径,那么大圆的面积是小圆面积的( )。
A. B.2倍 C.4倍
二、填空题
6.一只挂钟的时针长7厘米,转动一周,针尖走过的路程是( )厘米.
7.如图中4个圆的大小相同,则阴影部分表示的扇形面积最大的是( ),面积最小的是( )。
8.圆的半径一般用( )表示,直径用( )表示,面积公式用( )表示,周长公式用( )表示.
9.在一个长6厘米,宽4厘米的长方形内画一个最大的圆,这个圆的面积是( )平方厘米。
10.白居易的《府西池》中“柳元气力枝先动,池有波纹冰尽开”,描述了雨点打在水面上荡开层层波纹的情景。已知一个长方形水池的长是8m,宽是6m,当波纹到池边时,所形成的最大整圆的周长是( )m,面积是( )m2。
11.小刚量得一个树干的横截面的周长是125.6厘米,树干的横截面近似圆形,它的横截面大约是( )平方厘米。
12.李师傅想把3根横截面直径都是10cm的圆木用铁丝紧紧地捆绑在一起(如图),捆一圈(接头不计)至少需要铁丝( )cm,铁丝围成的图形面积是( )cm2。
13.一个圆的直径是12cm,它的周长是( )cm,面积是( )。
14.一个圆的周长扩大5倍,直径扩大( )倍,面积扩大( )。
15.下图中圆的周长是18.84dm,则圆的面积是( )dm2,正方形的面积是( )dm2。
三、判断题
16.半径越大,圆的面积越大. ( )
17.半圆的面积和周长分别是同直径圆面积和周长的一半。( )
18.一个圆的半径从4m增加到6m,这个圆的面积增加了6.28m2。( )
19.一个圆的半径扩大到原来的2倍,它的面积也扩大到原来的2倍。( )
20.在一张长6厘米、宽4厘米的长方形纸上剪一个面积最大的圆,这个圆的直径是4厘米。( )
四、计算题
21.计算下面圆环的面积。
22.求如图中阴影部分的周长和面积。
23.计算下图中阴影部分的面积。
五、解答题
24.沿着直径是8米的圆形水池周围铺一条1米宽的石子路,石子路占地面积是多少平方米?
25.用一根长30分米的绳子绕一根圆柱形柱子三圈后还多1.74分米,这根圆柱形柱子的直径是多少分米?
26.一个圆形音乐喷泉的周长是502.4米,喷泉外围修了一条宽4米的小路作为观赏区,观赏区外围的周长是多少米?
27.如图所示,一个运动场的两边是相同的半圆,中间是长方形,这个运动场的占地面积是多少平方米?
28.用20米长的铁条做直径是60厘米的圆形铁环,最多可以做多少个?
29.为进一步推进新农村建设,幸福新村新建了一个周长为94.2米的圆形花坛。为了便于游客观赏,村委会决定在花坛的四周铺一条环形的石子路,石子路宽1米。如果每平方米小路需要80千克石子,那么修这条路一共需要多少千克石子?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 B C B A C
1.B
【分析】甲图是外方内圆,圆的直径等于正方形边长;乙图是外圆内方,圆的直径等于正方形对角线,据此分别计算甲、乙的涂色部分面积,再比较大小解答。
【详解】甲图:正方形边长4×2=8(厘米)
涂色部分的面积是:82-3.14×42
=64-50.24
=13.76(平方厘米)
乙图:正方形对角线长是4×2=8(厘米)
涂色部分的面积是:3.14×42-8×4÷2×2
=50.24-32
=18.24(平方厘米)
因为18.24>13.76,所以乙图中涂色部分的面积大。
故答案为:B
【点睛】本题考查外方内圆和外圆内方图形的相关计算,解题关键是找到正方形与圆的半径的关联。
2.C
【分析】圆心决定圆的位置,半径决定圆的大小,同圆或等圆中直径是半径的2倍。据此解答。
【详解】A.圆心只决定圆的位置,不能决定圆的面积大小,原因错误;
B.所有圆的圆周率都相同,原因错误;
C.两个圆的直径不相等,则它们的半径不相等,那么两个圆的面积就不相等,原因正确;
D.圆的画法不同,不能决定圆的面积大小,原因错误。
故答案为:C
3.B
【分析】根据圆的面积公式:面积=π×半径2,代入数据,求出圆的面积,再根据比的意义,用大圆面积∶小圆面积,即可解答。
【详解】(π×62)∶(π×42)
=(36π)∶(16π)
=(36π÷4π)∶(16π÷4π)
=9∶4
两个圆的半径分别是6cm、4cm,大圆和小圆的面积比是9∶4。
故答案为:B
4.A
【分析】圆的直径÷2=半径,如果圆环的外圆直径是内圆直径的两倍,则它的外圆半径也是内圆半径的两倍。圆环的面积=外圆面积-内圆面积,设这个圆环的内圆半径是r,则外圆半径是2r,根据圆的面积公式S=πr2,分别求出内圆和外圆的面积,再把它们相减即可求出圆环的面积。据此解答。
【详解】设这个圆环的内圆半径是r,则外圆半径是2r。
外圆面积:π×(2r)2
=π×4r2
=4πr2
内圆面积:πr2
圆环面积:4πr2-πr2=3πr2
3πr2>πr2,则这个圆环的面积比内圆面积大。
故答案为:A
5.C
【分析】为了方便理解和计算,用设数法,设小圆的直径、大圆的半径都是2。根据圆的面积公式:S=πr2,分别计算出小圆和大圆的面积,再用大圆面积除以小圆的面积即可。
【详解】设小圆的直径、大圆的半径都是2。
小圆的半径是:2÷2=1
小圆的面积:π×12=π
大圆的面积:π×22=4π
大圆的面积是小圆面积的:
故答案为:C
【点睛】掌握用设数法解决问题的方法。
6.43.96
【解析】略
7. ④ ①
【分析】在同圆或等圆中,扇形的圆心角越大,扇形的面积越大。据此解答。
【详解】
从图中可知:>>>
则阴影部分表示的扇形面积最大的是④,面积最小的是①。
8. R d s=πr c=πd
【详解】略
9.12.56
【详解】长方形内最大的圆的直径等于长方形的最短边4厘米,据此利用圆的面积公式计算即可
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
10. 18.84 28.26
【详解】根据题意可知,在这个长方形水池中波纹所形成最大圆的直径就是这个长方形水池的宽即为是6米,根据圆的周长公式:C=πd,圆的面积公式;S=πr2,把数据代入公式解答。
【解答】3.14×6=18.84(m)
3.14×(6÷2)2
=3.14×32
=3.14×9
=28.26(m2)
则所形成的最大整圆的周长是18.84m,面积是28.26m2。
11.1256
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出树干的半径,再根据圆的面积公式:面积=π×半径2,代入数据,即可求出横截面的面积。
【详解】125.6÷3.14÷2
=40÷2
=20(厘米)
3.14×202
=3.14×400
=1256(平方厘米)
小刚量得一个树干的横截面的周长是125.6厘米,树干的横截面近似圆形,它的横截面大约是1256平方厘米。
12. 71.4 278.5
【分析】求捆一圈至少需要铁丝的长度,就是求图形的周长;图形最左边和最右边各有一个直径为10cm的半圆,可以组成一个圆;图形上面、下面的铁丝长度各相当于2条直径,所以铁丝的总长度=圆的周长+4条直径的长度,根据圆的周长公式C=πd,代入数据计算求解。
铁丝围成的图形面积=圆的面积+长方形的面积,其中圆的半径是(10÷2)cm,长方形的长是(10×2)cm,宽是10cm;根据圆的面积公式S=πr2,长方形的面积公式S=ab,代入数据计算求解。
【详解】3.14×10+10×4
=31.4+40
=71.4(cm)
3.14×(10÷2)2+(10×2)×10
=3.14×52+20×10
=3.14×25+200
=78.5+200
=278.5(cm2)
捆一圈(接头不计)至少需要铁丝71.4cm,铁丝围成的图形面积是278.5cm2。
13. 37.68 113.04
【分析】圆的周长=,圆的面积=,据此解答即可。
【详解】3.14×12=37.68(厘米)
3.14×(12÷2)2
=3.14×36
=113.04(平方厘米)
【点睛】本题考查圆的周长和面积,解答本题的关键是掌握圆的周长和面积计算公式。
14. 5 25
【详解】略
15. 28.26 18
【分析】将圆的周长除以3.14再除以2,求出圆的半径,从而根据圆面积S=πr2列式求出圆的面积;
将正方形沿着一条对角线一分为二,每个小三角形的底是圆的直径,高是圆的半径,根据三角形面积=底×高÷2,求出一个三角形的面积。将一个三角形的面积乘2,即可求出正方形的面积。
【详解】18.84÷3.14÷2=3(dm)
3.14×32=28.26(dm2)
(3×2)×3÷2×2
=6×3÷2×2
=18(dm2)
所以,圆的面积是28.26dm2,正方形的面积是18dm2。
【点睛】本题考查了圆的周长和面积、三角形的面积,熟记公式并灵活运用是解题的关键。
16.√
【解析】略
17.×
【分析】半圆的面积等于同直径圆面积的一半,半圆的周长等于同直径圆周长的一半加上直径。据此判断。
【详解】由分析可知,半圆的面积等于同直径圆面积的一半,而半圆的周长不等于同直径圆周长的一半。
所以原题说法错误。
故答案为:×
18.×
【分析】增加的部分是个圆环,根据圆环面积=圆周率×(大圆半径的平方-小圆半径的平方),列式计算即可。
【详解】3.14×(62-42)
=3.14×(36-16)
=3.14×20
=62.8(m2)
一个圆的半径从4m增加到6m,这个圆的面积增加了62.8m2,原说法错误。
故答案为:×
19.×
【分析】此题考查了积的变化规律在圆的面积公式中的灵活应用,这里可得结论:圆的半径扩大n倍,则这个圆的面积就扩大n的平方倍。圆的面积=π×r×r,其中π是一个定值,根据积的变化规律:一个因数不变,另一个因数扩大几倍,积就扩大几倍,即可解答。
【详解】圆的面积=π×r×r,r扩大2倍,则圆的面积就扩大:2×2=4倍,所以原题说法错误。
故答案为:×
20.√
【分析】在长方形纸上剪一个面积最大的圆,圆的直径=长方形的宽,据此分析。
【详解】在一张长6厘米、宽4厘米的长方形纸上剪一个面积最大的圆,这个圆的直径是4厘米,说法正确。
故答案为:√
21.197.82cm2
【分析】从图中可知,大圆的半径R是12cm,小圆的半径r是9cm;根据圆环的面积公式S环=π(R2-r2),代入数据计算,求出圆环的面积。
【详解】3.14×(122-92)
=3.14×(144-81)
=3.14×63
=197.82(cm2)
圆环的面积是197.82cm2。
22.阴影部分的周长是71.4厘米,面积是121.5平方厘米
【分析】通过观察可知,阴影部分的周长等于圆的周长加上2条20厘米的线段的长,面积等于长方形面积减去圆的面积,圆的直径相当于长方形的宽,也就是10厘米,根据长方形的面积=长×宽、圆周长公式:C=πd、圆面积公式:S=πr2,代入数据计算即可。
【详解】3.14×10+20×2
=31.4+40
=71.4(厘米)
20×10-3.14×(10÷2)2
=20×10-3.14×52
=200-3.14×25
=200-78.5
=121.5(平方厘米)
阴影部分的周长是71.4厘米,面积是121.5平方厘米。
23.78.5平方厘米
【分析】由图可知,外部大圆直径是20厘米,内部小圆是以大圆的半径为直径。阴影部分的面积等于直径是20厘米的半圆面积减去直径是10厘米的整圆面积,据此解答。
【详解】3.14×(20÷2)2÷2-3.14×(20÷2÷2)2
=3.14×102÷2-3.14×52
=3.14×100÷2-3.14×25
=157-78.5
=78.5(平方厘米)
阴影部分面积是78.5平方厘米。
24.28.26平方米
【分析】求石子路的占地面积就是求圆环的面积,根据圆环的面积公式:S=-,据此进行计算即可。
【详解】8÷2=4(米)
4+1=5(米)
3.14×-3.14×42
=3.14×25-3.14×16
=3.14×(25-16)
=3.14×9
=28.26(平方米)
答:石子路占地面积是28.26平方米。
25.3分米
【分析】用这个绳子的长度减去剩余的1.74分米,求出这个柱子底面周长的3倍,再除以3求出柱子的底面周长,然后根据圆的周长公式:C=πd,那么d=C÷π,把数据代入公式解答。
【详解】(30-1.74)÷3÷3.14
=28.26÷3÷3.14
=9.42÷3.14
=3(分米)
答:这个柱子的直径是3分米。
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
26.527.52米
【分析】一个圆形音乐喷泉的周长是502.4米,根据圆的周长=,得出圆的半径是80米,喷泉外围修了一条宽4米的小路作为观赏区,则外面的圆是一个半径是84米,根据圆的周长公式求出圆的周长。
【详解】502.4÷3.14=160(米)
160÷2=80(米)
(80+4)×2×3.14
=84×2×3.14
=527.52(米)
答:观赏区外围的周长是527.52米。
27.1314平方米
【分析】根据图可知,左右两边是两个半圆形,则相当于一个直径是20米的圆,中间是长方形,长是50米,宽是20米,根据圆的面积公式:,长方形的面积=长×宽,把数代入求出这两部分的面积,再相加即可。
【详解】
=3.14×100+1000
=314+1000
=1314(平方米)
答:这个运动场的面积是1314平方米。
28.10个
【分析】根据圆的周长公式:周长=π×直径,代入数据,求出圆形铁环的周长,再用铁条的长度÷圆形铁环的周长,最后无论剩下多少厘米铁条,只要不够一个圆形铁环就无法制作一个铁环,结果用“去尾法”取整数,据此解答,注意单位名数的统一。
【详解】20米=2000厘米
2000÷(3.14×60)
=2000÷188.4
≈10(个)
答:最大可以做10个。
29.7787.2千克
【分析】根据圆周长公式:C=2πr,代入数据即可求出花坛的半径,再加上1米,即可求出石子路外圆的半径,然后根据圆环的面积公式:S=π(R2-r2),求出小路的面积即可;再乘80千克,即可求出石子的总千克数。
【详解】94.2÷3.14÷2
=30÷2
=15(米)
15+1=16(米)
3.14×162-3.14×152
=3.14×256-3.14×225
=803.84-706.5
=97.34(平方米)
97.34×80=7787.2(千克)
答:修这条路一共需要7787.2千克石子。
答案第11页,共22页
答案第11页,共22页
