人教版四年级数学第三单元测试卷(含答案)
文档属性
| 名称 | 人教版四年级数学第三单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 137.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 10:54:42 | ||
图片预览

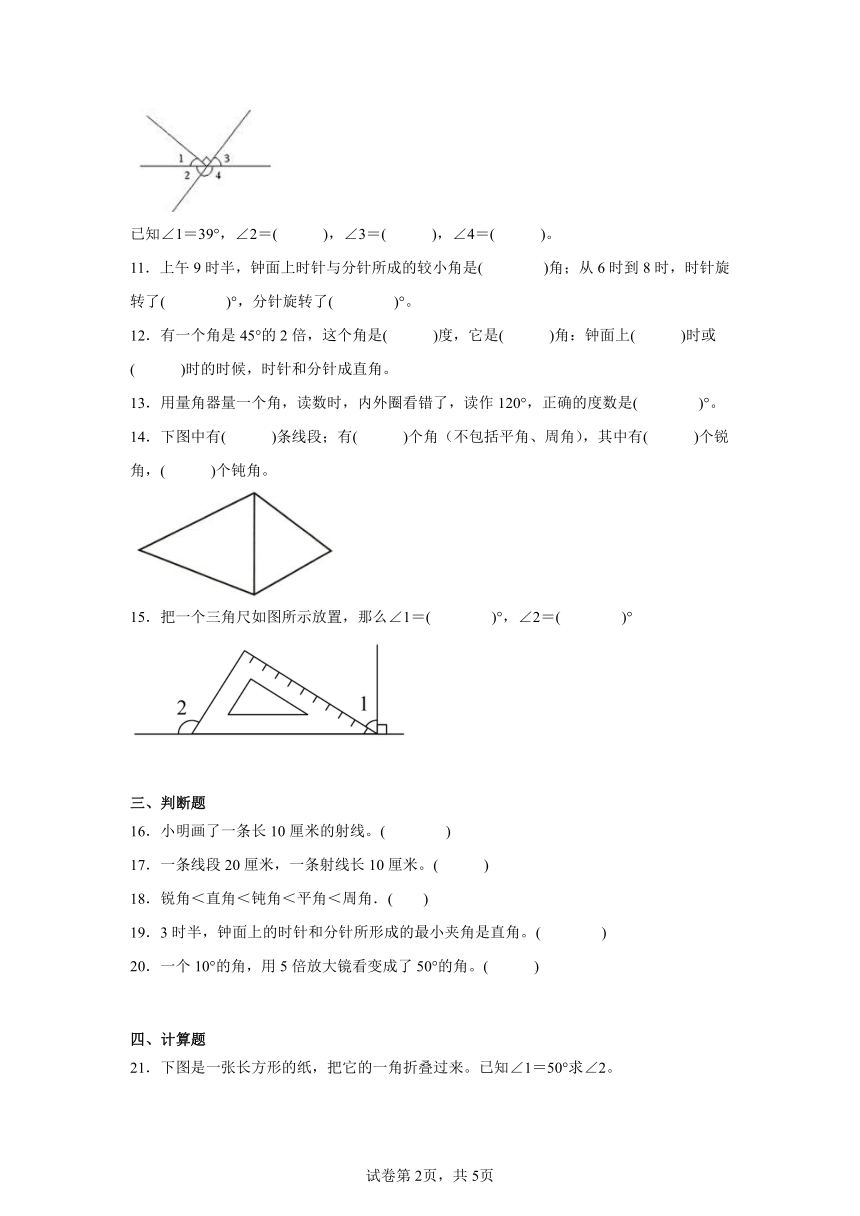

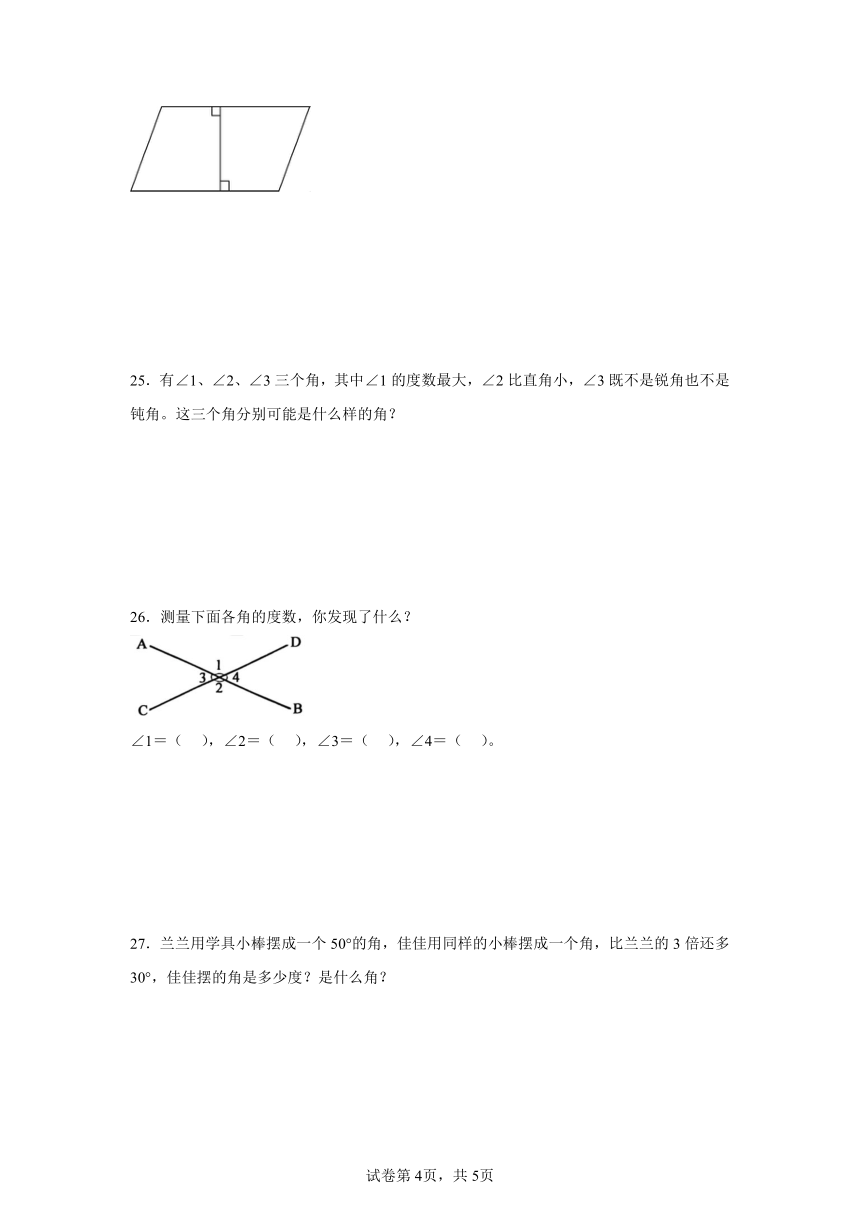

文档简介
四年级数学第三单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.能向两端无线延伸的是( )。
A.直线 B.射线 C.线段
2.小芳画了一条长3厘米8毫米的( )。
A.线段 B.射线 C.直线
3.下面说法正确的是( )。
A.钝角总比锐角大 B.一条直线就是一个平角 C.公顷是面积单位,平方千米是长度单位
4.用一副三角板可以画出的角是( )。
A.40° B.160° C.120°
5.用一副三角尺,不能拼出( )的角。
A.75° B.135° C.155° D.180°
二、填空题
6.周角=( )度,平角=( )度。
7.( )都可以无限延伸,其中( )没有端点,( )只有一个端点。
8.
上图中,( )是直线,( )是射线,( )是线段。
9.1个直角和1个锐角可以拼成1个( )角。
10.看图填空。
已知∠1=39°,∠2=( ),∠3=( ),∠4=( )。
11.上午9时半,钟面上时针与分针所成的较小角是( )角;从6时到8时,时针旋转了( )°,分针旋转了( )°。
12.有一个角是45°的2倍,这个角是( )度,它是( )角:钟面上( )时或( )时的时候,时针和分针成直角。
13.用量角器量一个角,读数时,内外圈看错了,读作120°,正确的度数是( )°。
14.下图中有( )条线段;有( )个角(不包括平角、周角),其中有( )个锐角,( )个钝角。
15.把一个三角尺如图所示放置,那么∠1=( )°,∠2=( )°
三、判断题
16.小明画了一条长10厘米的射线。( )
17.一条线段20厘米,一条射线长10厘米。( )
18.锐角<直角<钝角<平角<周角.( )
19.3时半,钟面上的时针和分针所形成的最小夹角是直角。( )
20.一个10°的角,用5倍放大镜看变成了50°的角。( )
四、计算题
21.下图是一张长方形的纸,把它的一角折叠过来。已知∠1=50°求∠2。
22.如下图,已知∠1=∠2=25°,求∠3、∠4、∠5的度数。
23.如图,求,,的度数。
五、解答题
24.请数一数,如图中有几个锐角、几个直角、几个钝角和几个平角。
25.有∠1、∠2、∠3三个角,其中∠1的度数最大,∠2比直角小,∠3既不是锐角也不是钝角。这三个角分别可能是什么样的角?
26.测量下面各角的度数,你发现了什么?
∠1=( ),∠2=( ),∠3=( ),∠4=( )。
27.兰兰用学具小棒摆成一个50°的角,佳佳用同样的小棒摆成一个角,比兰兰的3倍还多30°,佳佳摆的角是多少度?是什么角?
28.已知:∠3=∠1+∠2,∠3=128°,∠1=63°
求:∠2=?
29.小乐用一副三角尺在一块长方形纸板上拼出了下面的图形(图中的阴影部分),爸爸说∠1=30°,请求出∠2的度数。
30.数一数,下图中共有多少个角?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 A A A C C
1.A
【分析】根据直线的定义可知,直线是直的,且无头无尾,没有端点,可以向两个方向无限地延伸。据此选择即可。
【详解】由分析可知,能向两端无线延伸的是直线。
故答案为:A
2.A
【分析】直线无端点,无限长,不可以度量;射线只有一个端点,无限长,不可以度量;线段有2个端点,有限长,可以度量;据此根据直线、射线和线段的定义进行作答。
【详解】根据分析,小芳画的这条线长3厘米8毫米有具体的长度,所以她画的是一条线段。
故答案为:A
3.A
【分析】从一点引出两条射线所组成的图形叫做角。小于90°的角叫锐角,等于90°的角叫直角,大于90°小于180°的角叫钝角,等于180°的角叫平角。常用面积单位有平方厘米、平方分米、平方米、平方千米、公顷。
【详解】A.小于90°的角叫锐角,大于90°小于180°的角叫钝角,钝角总比锐角大说法正确。
B.平角是由一条射线绕着它的端点旋转,当终边和始边在同一条直线上,方向相反时所形成的角,一条直线就是一个平角说法错误。
C.公顷和平方千米都是面积单位,公顷是面积单位,平方千米是长度单位说法错误。
说法正确的是:钝角总比锐角大。
故答案为:A
4.C
【分析】一副三角板,一个三角板的角有30°、60°、90°,等腰直角三角板的角有45°、45°、90°,用它们进行加减,看能否得出这几个角度即可。
【详解】A.30°+10°=40°,90°-50°=40°,60°-60°=40°,两个三角板无法画出40°。
B.90°+90°=180°,90°+60°=150°两个三角板无法画出160°。
C.90°+30°=120°,即两个三角板可以画出120°。
故答案为:C
5.C
【分析】一副三角板中包含的角的度数有30°、45°(两个)、60°、90°(两个),如果把它们相加或相减后能得出的角都可以用一副三角板拼出。
【详解】A.75°=30°+45°,它可以用一副三角板拼出。
B.135°=90°+45°,它可以用一副三角板拼出。
C.155°它不可以用一副三角板拼出。
D.180°=90°+90°,它可以用一副三角尺拼出。
故答案为:C
6. 360 180
【分析】依据角的概念及分类即可作答。小于90度的角是锐角,等于90度的角是直角,大于90度且小于180度的角是钝角,等于180度的角是平角,等于360度的角是周角。
【详解】周角=360度,平角=180度。
【点睛】此题主要考查了周角和平角的含义,是需要熟记的内容。
7. 直线和射线 直线 射线
【分析】直线是经过两点的一条线;射线是直线上的一点和它一旁的部分。直线两端都没有端点、可以向两端无限延伸、不可测量长度;射线向一方无限延伸,它有一个端点。直线是轴对称图形,它有无数条对称轴,其中一条是它本身,还有任意一条与它垂直的直线;射线不是轴对称图形。
【详解】由分析可得:直线和射线都可以无限延伸,其中直线没有端点,射线只有一个端点。
8. ② ④ ①
【分析】直线上任意两点之间的一段叫做线段,线段有两个端点。把线段的两端无限延长,得到一条直线,直线没有端点。把线段的一端无限延长,得到一条射线,射线有一个端点。
【详解】上图中,②是直线,④是射线,①是线段。
【点睛】本题考查直线、射线和线段的特征,这三种图形都是直的线,直线没有端点,射线有一个端点,线段有两个端点。
9.钝
【分析】直角等于90°,锐角小于90°,钝角大于90°且小于180°,1个直角加1个锐角的度数大于90°小于180°,据此填空即可。
【详解】1个直角和1个锐角可以拼成1个钝角。
10. 51° 51° 129°
【分析】根据题图可知,∠1、∠3和一个直角组成一个平角,则∠3=180°-90°-∠1。∠1、∠2和一个直角组成一个平角,则∠2=∠3。∠2和∠4组成一个平角,则∠4=180°-∠2。
【详解】∠3=180°-90°-∠1
=180°-90°-39°
=90°-39°
=51°
∠2=∠3=51°
∠4=180°-∠2
=180°-51°
=129°
已知∠1=39°,∠2=51°,∠3=51°,∠4=129°。
11. 钝 60 720
【分析】根据对钟面的了解,平均分为12大格,每大格的度数是30°,9时半,时针指向9和10之间,分针指向6,则较小的角大于3大格的度数且小于4大格的度数,大于3×30°,小于4×30°;从6时到8时,时针走了2大格,旋转了2×30°;分针转了2圈,则旋转了2×360°,据此填空即可。
【详解】3×30°=90°,4×30°=120°,90°<较小角<120°;
2×30°=60°,2×360°=720°
上午9时半,钟面上时针与分针所成的较小角是钝角;从6时到8时,时针旋转了60°,分针旋转了720°。
12. 90 直 3 9
【分析】根据倍数关系可得,这个角是45°×2=90(度),是直角;钟表上共有12个空格,每个空格是30°,90°的角需要分针与时针之间有3个空格,在早晚3点或早晚9点的时间恰好成90°。
【详解】45°×2=90(度)
有一个角是45°的2倍,这个角是90度,它是直角:钟面上3时或9时的时候,时针和分针成直角。
13.60°
【分析】量角时中心与角的顶点对齐,0°刻度线与角的一条边对齐,另一条边对着刻度几就是几度。读数时内外圈看错了,即假如角的一条边与内圈的0°刻度线对齐,另一条边与外圈的120°刻度线对齐,则实际角的度数为180°-120°=60°。
【详解】180°-120°=60°
则正确的度数是60°。
【点睛】本题考查量角器的正确用法。读数时,0刻度线在外圈就看外圈刻度,0刻度线在内圈就看内圈刻度。
14. 5 8 6 2
【分析】线段是直的,有两个端点,可测量。从一点引出两条射线所形成的图形叫做角。和书本的角相等大小的是直角,比直角大的是钝角,比直角小的是锐角,由此解答。
【详解】图中有5条线段;有8个角(不包括平角、周角),其中有6个锐角,2个钝角。
15. 60 120
【分析】根据直角三角尺的内角角度分别是90°、60°、30°,平角是180°,图中标出一个直角,那么三角尺的30°角和∠1组成一个直角,让90°-30°即可求解∠1;∠2和三角尺的60°角组成一个平角,让180°-60°即可求解∠2,据此解答。
【详解】∠1=90°-30°=60°
∠2=180°-60°=120°
把一个三角尺如图所示放置,那么∠1=(60)°,∠2=(120)°
16.×
【分析】根据射线的定义可得:射线只有1个端点,无法测量长度,据此判断即可。
【详解】射线的长度不能度量,原题说法错误。
故答案为:×
17.×
【分析】线段有两个端点,长度可以度量;射线只有一个端点,可以向一端无限延伸,不可测量长度。
【详解】根据解析可知,可以说一条线段20厘米,但不能说一条射线长10厘米,原题表达错误。
故答案为:×
18.√
【解析】略
19.×
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°;3时半时,分针指向6,时针指在3与4的中间,时针与分钟之间有2个半大格,时针与分针之间的夹角是:30°×2+30°÷2=75°,根据角的分类标准可知,是锐角,故原题干说法错误。
【详解】30°×2+30°÷2
=60°+15°
=75°
所以,3时半,钟面上的时针和分针所形成的最小夹角是直角,是错误的。
故答案为:×
【点睛】钟面上每个大格是30°,时针和分针之间有几个大格,夹角就是几个30°。
20.×
【分析】根据角的定义,有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边。决定角的大小是两条边张开的大小,用放大镜看角,角的度数不变,据此解答。
【详解】把一个10°的角,用5倍放大镜看,我们看到的角仍是10°的角。原说法错误。
故答案为:×
21.80°
【分析】由图可以看出是一张长方形纸折起来的图形,把这张纸展开后,以∠1、∠2的顶点为顶点的角是180°,由于∠1盖住了一个和它相等的角,展开后就是2∠1+∠2=180°,又知∠1=50°,据此可求出∠2的度数。
【详解】∠2=180°-2×∠1
=180°-2×50°
=180°-100°
=80°
即∠2=80°
22.∠3=130°;∠4=130°;∠5=50°
【分析】观察图形可知,∠1、∠2与∠3组成了一个平角,所以∠3=180°-∠1-∠2;∠3与∠5组成了一个平角,所以∠5=180°-∠3;∠3与∠5组成一个平角,∠4与∠5也组成一个平角,所以∠3=∠4,代入数据计算即可。
【详解】∠3=180°-∠1-∠2=180°-25°-25°=155°-25°=130°
∠3=∠4=130°
∠5=180°-∠3=180°-130°=50°
23.∠1=50°;∠2=40°;∠3=140°
【分析】由图可知,∠1和直角以及40°的角组成了一个平角。求∠1的度数,直接用180°减去90°再减去40°即可解答;∠2和∠1以及直角组成了一个平角。求∠2的度数,直接用180°减去∠1的度数再减去90°即可解答;∠3和40°的角组成了一个平角。求∠3的度数,直接用180°减去40°即可解答。
【详解】∠1=180°-90°-40°=90°-40°=50°
∠2=180°-∠1-90°=180°-50°-90°=130°-90°=40°
∠3=180°-40°=140°
即∠1=50°,∠2=40°,∠3=140°。
24.2个锐角,4个直角,2个钝角,2个平角
【分析】小于90°的角叫做锐角,90°的角叫做直角,大于90°小于180°的角叫做钝角,180°的角叫做平角,据此解答。
【详解】图中有2个锐角,4个直角,2个钝角,2个平角。
【点睛】熟练掌握锐角、直角、钝角和平角的定义是解决本题的关键。
25.∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
【分析】因为比直角小的角是锐角,所以∠2是锐角,因为∠3 既不是锐角也不是钝角,所以∠3可能是直角,也可能是平角;又因为在∠1、∠2、∠3三个角中,∠1的度数最大,所以∠3为直角,∠1为平角,若∠3是平角,则∠1是周角。
【详解】根据分析:∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
26.130°;130°;50°;50°;发现见详解过程
【分析】根据角度量的方法,量角要注意两对齐:量角器的中心和角的顶点对齐,量角器的0刻度线和角的一条边对齐,做到两对齐后看角的另一条边对着刻度线几,这个角就是几度,看刻度要分清内外圈,据此量出各个角的度数;再根据各角度数的大小,去看发现了什么。
【详解】
∠1=130°,∠2=130°,∠3=50°,∠4=50°。
发现:∠1=∠2,∠3=∠4,即:两条直线相交所成的角中,相对的两个角的度数相等。(答案不唯一)
27.180°;平角
【分析】根据题意,用兰兰摆的角的度数乘3再加上30°,就是佳佳摆的角的度数,再根据角的分类:大于0°小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角;进行判定即可。
【详解】50°×3+30°
=150°+30°
=180°
答:佳佳摆的角是180°,是平角。
28.65°
【详解】试题分析:因为∠3=∠1+∠2,所以∠2=∠3﹣∠1,由此求解.
解:∠2=∠3﹣∠1=128°﹣63°=65°;
答:∠2是65°.
点评:本题根据一个加数=和﹣另一个加数进行求解.
29.45°
【分析】根据题图可知,∠1、∠2和三角尺中60°、45°的角组成一个平角,则∠2=180°-∠1-60°-45°。
【详解】∠2=180°-∠1-60°-45°=180°-30°-60°-45°=45°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角)、三角尺中各个角,以及它与各角之间的关系,利用已知角,求出未知角。
30.21个
【分析】类似于数线段的方法,图中有6个基本的角,这些角又可以2个、3个、4个、5个、6个组合在一起,求出每一种的数量,相加得到总数。
【详解】
答:图中共有21个角。
【点睛】一个大的角被分成n个角,那么总共可以数出个角。
答案第11页,共22页
答案第11页,共22页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.能向两端无线延伸的是( )。
A.直线 B.射线 C.线段
2.小芳画了一条长3厘米8毫米的( )。
A.线段 B.射线 C.直线
3.下面说法正确的是( )。
A.钝角总比锐角大 B.一条直线就是一个平角 C.公顷是面积单位,平方千米是长度单位
4.用一副三角板可以画出的角是( )。
A.40° B.160° C.120°
5.用一副三角尺,不能拼出( )的角。
A.75° B.135° C.155° D.180°
二、填空题
6.周角=( )度,平角=( )度。
7.( )都可以无限延伸,其中( )没有端点,( )只有一个端点。
8.
上图中,( )是直线,( )是射线,( )是线段。
9.1个直角和1个锐角可以拼成1个( )角。
10.看图填空。
已知∠1=39°,∠2=( ),∠3=( ),∠4=( )。
11.上午9时半,钟面上时针与分针所成的较小角是( )角;从6时到8时,时针旋转了( )°,分针旋转了( )°。
12.有一个角是45°的2倍,这个角是( )度,它是( )角:钟面上( )时或( )时的时候,时针和分针成直角。
13.用量角器量一个角,读数时,内外圈看错了,读作120°,正确的度数是( )°。
14.下图中有( )条线段;有( )个角(不包括平角、周角),其中有( )个锐角,( )个钝角。
15.把一个三角尺如图所示放置,那么∠1=( )°,∠2=( )°
三、判断题
16.小明画了一条长10厘米的射线。( )
17.一条线段20厘米,一条射线长10厘米。( )
18.锐角<直角<钝角<平角<周角.( )
19.3时半,钟面上的时针和分针所形成的最小夹角是直角。( )
20.一个10°的角,用5倍放大镜看变成了50°的角。( )
四、计算题
21.下图是一张长方形的纸,把它的一角折叠过来。已知∠1=50°求∠2。
22.如下图,已知∠1=∠2=25°,求∠3、∠4、∠5的度数。
23.如图,求,,的度数。
五、解答题
24.请数一数,如图中有几个锐角、几个直角、几个钝角和几个平角。
25.有∠1、∠2、∠3三个角,其中∠1的度数最大,∠2比直角小,∠3既不是锐角也不是钝角。这三个角分别可能是什么样的角?
26.测量下面各角的度数,你发现了什么?
∠1=( ),∠2=( ),∠3=( ),∠4=( )。
27.兰兰用学具小棒摆成一个50°的角,佳佳用同样的小棒摆成一个角,比兰兰的3倍还多30°,佳佳摆的角是多少度?是什么角?
28.已知:∠3=∠1+∠2,∠3=128°,∠1=63°
求:∠2=?
29.小乐用一副三角尺在一块长方形纸板上拼出了下面的图形(图中的阴影部分),爸爸说∠1=30°,请求出∠2的度数。
30.数一数,下图中共有多少个角?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 A A A C C
1.A
【分析】根据直线的定义可知,直线是直的,且无头无尾,没有端点,可以向两个方向无限地延伸。据此选择即可。
【详解】由分析可知,能向两端无线延伸的是直线。
故答案为:A
2.A
【分析】直线无端点,无限长,不可以度量;射线只有一个端点,无限长,不可以度量;线段有2个端点,有限长,可以度量;据此根据直线、射线和线段的定义进行作答。
【详解】根据分析,小芳画的这条线长3厘米8毫米有具体的长度,所以她画的是一条线段。
故答案为:A
3.A
【分析】从一点引出两条射线所组成的图形叫做角。小于90°的角叫锐角,等于90°的角叫直角,大于90°小于180°的角叫钝角,等于180°的角叫平角。常用面积单位有平方厘米、平方分米、平方米、平方千米、公顷。
【详解】A.小于90°的角叫锐角,大于90°小于180°的角叫钝角,钝角总比锐角大说法正确。
B.平角是由一条射线绕着它的端点旋转,当终边和始边在同一条直线上,方向相反时所形成的角,一条直线就是一个平角说法错误。
C.公顷和平方千米都是面积单位,公顷是面积单位,平方千米是长度单位说法错误。
说法正确的是:钝角总比锐角大。
故答案为:A
4.C
【分析】一副三角板,一个三角板的角有30°、60°、90°,等腰直角三角板的角有45°、45°、90°,用它们进行加减,看能否得出这几个角度即可。
【详解】A.30°+10°=40°,90°-50°=40°,60°-60°=40°,两个三角板无法画出40°。
B.90°+90°=180°,90°+60°=150°两个三角板无法画出160°。
C.90°+30°=120°,即两个三角板可以画出120°。
故答案为:C
5.C
【分析】一副三角板中包含的角的度数有30°、45°(两个)、60°、90°(两个),如果把它们相加或相减后能得出的角都可以用一副三角板拼出。
【详解】A.75°=30°+45°,它可以用一副三角板拼出。
B.135°=90°+45°,它可以用一副三角板拼出。
C.155°它不可以用一副三角板拼出。
D.180°=90°+90°,它可以用一副三角尺拼出。
故答案为:C
6. 360 180
【分析】依据角的概念及分类即可作答。小于90度的角是锐角,等于90度的角是直角,大于90度且小于180度的角是钝角,等于180度的角是平角,等于360度的角是周角。
【详解】周角=360度,平角=180度。
【点睛】此题主要考查了周角和平角的含义,是需要熟记的内容。
7. 直线和射线 直线 射线
【分析】直线是经过两点的一条线;射线是直线上的一点和它一旁的部分。直线两端都没有端点、可以向两端无限延伸、不可测量长度;射线向一方无限延伸,它有一个端点。直线是轴对称图形,它有无数条对称轴,其中一条是它本身,还有任意一条与它垂直的直线;射线不是轴对称图形。
【详解】由分析可得:直线和射线都可以无限延伸,其中直线没有端点,射线只有一个端点。
8. ② ④ ①
【分析】直线上任意两点之间的一段叫做线段,线段有两个端点。把线段的两端无限延长,得到一条直线,直线没有端点。把线段的一端无限延长,得到一条射线,射线有一个端点。
【详解】上图中,②是直线,④是射线,①是线段。
【点睛】本题考查直线、射线和线段的特征,这三种图形都是直的线,直线没有端点,射线有一个端点,线段有两个端点。
9.钝
【分析】直角等于90°,锐角小于90°,钝角大于90°且小于180°,1个直角加1个锐角的度数大于90°小于180°,据此填空即可。
【详解】1个直角和1个锐角可以拼成1个钝角。
10. 51° 51° 129°
【分析】根据题图可知,∠1、∠3和一个直角组成一个平角,则∠3=180°-90°-∠1。∠1、∠2和一个直角组成一个平角,则∠2=∠3。∠2和∠4组成一个平角,则∠4=180°-∠2。
【详解】∠3=180°-90°-∠1
=180°-90°-39°
=90°-39°
=51°
∠2=∠3=51°
∠4=180°-∠2
=180°-51°
=129°
已知∠1=39°,∠2=51°,∠3=51°,∠4=129°。
11. 钝 60 720
【分析】根据对钟面的了解,平均分为12大格,每大格的度数是30°,9时半,时针指向9和10之间,分针指向6,则较小的角大于3大格的度数且小于4大格的度数,大于3×30°,小于4×30°;从6时到8时,时针走了2大格,旋转了2×30°;分针转了2圈,则旋转了2×360°,据此填空即可。
【详解】3×30°=90°,4×30°=120°,90°<较小角<120°;
2×30°=60°,2×360°=720°
上午9时半,钟面上时针与分针所成的较小角是钝角;从6时到8时,时针旋转了60°,分针旋转了720°。
12. 90 直 3 9
【分析】根据倍数关系可得,这个角是45°×2=90(度),是直角;钟表上共有12个空格,每个空格是30°,90°的角需要分针与时针之间有3个空格,在早晚3点或早晚9点的时间恰好成90°。
【详解】45°×2=90(度)
有一个角是45°的2倍,这个角是90度,它是直角:钟面上3时或9时的时候,时针和分针成直角。
13.60°
【分析】量角时中心与角的顶点对齐,0°刻度线与角的一条边对齐,另一条边对着刻度几就是几度。读数时内外圈看错了,即假如角的一条边与内圈的0°刻度线对齐,另一条边与外圈的120°刻度线对齐,则实际角的度数为180°-120°=60°。
【详解】180°-120°=60°
则正确的度数是60°。
【点睛】本题考查量角器的正确用法。读数时,0刻度线在外圈就看外圈刻度,0刻度线在内圈就看内圈刻度。
14. 5 8 6 2
【分析】线段是直的,有两个端点,可测量。从一点引出两条射线所形成的图形叫做角。和书本的角相等大小的是直角,比直角大的是钝角,比直角小的是锐角,由此解答。
【详解】图中有5条线段;有8个角(不包括平角、周角),其中有6个锐角,2个钝角。
15. 60 120
【分析】根据直角三角尺的内角角度分别是90°、60°、30°,平角是180°,图中标出一个直角,那么三角尺的30°角和∠1组成一个直角,让90°-30°即可求解∠1;∠2和三角尺的60°角组成一个平角,让180°-60°即可求解∠2,据此解答。
【详解】∠1=90°-30°=60°
∠2=180°-60°=120°
把一个三角尺如图所示放置,那么∠1=(60)°,∠2=(120)°
16.×
【分析】根据射线的定义可得:射线只有1个端点,无法测量长度,据此判断即可。
【详解】射线的长度不能度量,原题说法错误。
故答案为:×
17.×
【分析】线段有两个端点,长度可以度量;射线只有一个端点,可以向一端无限延伸,不可测量长度。
【详解】根据解析可知,可以说一条线段20厘米,但不能说一条射线长10厘米,原题表达错误。
故答案为:×
18.√
【解析】略
19.×
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°;3时半时,分针指向6,时针指在3与4的中间,时针与分钟之间有2个半大格,时针与分针之间的夹角是:30°×2+30°÷2=75°,根据角的分类标准可知,是锐角,故原题干说法错误。
【详解】30°×2+30°÷2
=60°+15°
=75°
所以,3时半,钟面上的时针和分针所形成的最小夹角是直角,是错误的。
故答案为:×
【点睛】钟面上每个大格是30°,时针和分针之间有几个大格,夹角就是几个30°。
20.×
【分析】根据角的定义,有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边。决定角的大小是两条边张开的大小,用放大镜看角,角的度数不变,据此解答。
【详解】把一个10°的角,用5倍放大镜看,我们看到的角仍是10°的角。原说法错误。
故答案为:×
21.80°
【分析】由图可以看出是一张长方形纸折起来的图形,把这张纸展开后,以∠1、∠2的顶点为顶点的角是180°,由于∠1盖住了一个和它相等的角,展开后就是2∠1+∠2=180°,又知∠1=50°,据此可求出∠2的度数。
【详解】∠2=180°-2×∠1
=180°-2×50°
=180°-100°
=80°
即∠2=80°
22.∠3=130°;∠4=130°;∠5=50°
【分析】观察图形可知,∠1、∠2与∠3组成了一个平角,所以∠3=180°-∠1-∠2;∠3与∠5组成了一个平角,所以∠5=180°-∠3;∠3与∠5组成一个平角,∠4与∠5也组成一个平角,所以∠3=∠4,代入数据计算即可。
【详解】∠3=180°-∠1-∠2=180°-25°-25°=155°-25°=130°
∠3=∠4=130°
∠5=180°-∠3=180°-130°=50°
23.∠1=50°;∠2=40°;∠3=140°
【分析】由图可知,∠1和直角以及40°的角组成了一个平角。求∠1的度数,直接用180°减去90°再减去40°即可解答;∠2和∠1以及直角组成了一个平角。求∠2的度数,直接用180°减去∠1的度数再减去90°即可解答;∠3和40°的角组成了一个平角。求∠3的度数,直接用180°减去40°即可解答。
【详解】∠1=180°-90°-40°=90°-40°=50°
∠2=180°-∠1-90°=180°-50°-90°=130°-90°=40°
∠3=180°-40°=140°
即∠1=50°,∠2=40°,∠3=140°。
24.2个锐角,4个直角,2个钝角,2个平角
【分析】小于90°的角叫做锐角,90°的角叫做直角,大于90°小于180°的角叫做钝角,180°的角叫做平角,据此解答。
【详解】图中有2个锐角,4个直角,2个钝角,2个平角。
【点睛】熟练掌握锐角、直角、钝角和平角的定义是解决本题的关键。
25.∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
【分析】因为比直角小的角是锐角,所以∠2是锐角,因为∠3 既不是锐角也不是钝角,所以∠3可能是直角,也可能是平角;又因为在∠1、∠2、∠3三个角中,∠1的度数最大,所以∠3为直角,∠1为平角,若∠3是平角,则∠1是周角。
【详解】根据分析:∠2是锐角,∠3是直角,则∠1是钝角;∠2是锐角,若∠3是平角,则∠1是周角。
26.130°;130°;50°;50°;发现见详解过程
【分析】根据角度量的方法,量角要注意两对齐:量角器的中心和角的顶点对齐,量角器的0刻度线和角的一条边对齐,做到两对齐后看角的另一条边对着刻度线几,这个角就是几度,看刻度要分清内外圈,据此量出各个角的度数;再根据各角度数的大小,去看发现了什么。
【详解】
∠1=130°,∠2=130°,∠3=50°,∠4=50°。
发现:∠1=∠2,∠3=∠4,即:两条直线相交所成的角中,相对的两个角的度数相等。(答案不唯一)
27.180°;平角
【分析】根据题意,用兰兰摆的角的度数乘3再加上30°,就是佳佳摆的角的度数,再根据角的分类:大于0°小于90°的角是锐角,等于90°的角是直角,大于90°小于180°的角是钝角,等于180°的角是平角;进行判定即可。
【详解】50°×3+30°
=150°+30°
=180°
答:佳佳摆的角是180°,是平角。
28.65°
【详解】试题分析:因为∠3=∠1+∠2,所以∠2=∠3﹣∠1,由此求解.
解:∠2=∠3﹣∠1=128°﹣63°=65°;
答:∠2是65°.
点评:本题根据一个加数=和﹣另一个加数进行求解.
29.45°
【分析】根据题图可知,∠1、∠2和三角尺中60°、45°的角组成一个平角,则∠2=180°-∠1-60°-45°。
【详解】∠2=180°-∠1-60°-45°=180°-30°-60°-45°=45°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角)、三角尺中各个角,以及它与各角之间的关系,利用已知角,求出未知角。
30.21个
【分析】类似于数线段的方法,图中有6个基本的角,这些角又可以2个、3个、4个、5个、6个组合在一起,求出每一种的数量,相加得到总数。
【详解】
答:图中共有21个角。
【点睛】一个大的角被分成n个角,那么总共可以数出个角。
答案第11页,共22页
答案第11页,共22页
