人教版 五年级数学上册 第四单元 可能性测试卷(含答案)
文档属性
| 名称 | 人教版 五年级数学上册 第四单元 可能性测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 176.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览




文档简介
五年级数学第四单元测试卷
一、选择题
1.小明的年龄( )比他爸爸的年龄小。
A.一定 B.可能 C.不可能
2.下列成语反映的事件中,可能性最小的是( )。
A.旭日东升 B.守株待兔 C.夕阳西下 D.日月交替
3.明明抛一枚硬币,共抛了9次,其中正面朝上5次,反面4次。如果抛第10次,则( )。
A.正面朝上的可能性大 B.反面朝上的可能性大
C.正面、反面朝上的可能性一样大 D.无法判断
4.从一个口袋里摸球,摸了10次也没有摸到红球,说明口袋里( )红球。
A.一定没有 B.可能没有 C.一定有
5.一个盒子里只有相同数量的红球和黑球,小丽从中摸出一个球,( )是白球。
A.可能 B.不可能 C.一定
6.小明和小红玩飞行棋,下面的确定先后顺序的方法不公平的是( )。
A.用“剪刀石头布”的猜拳方法,赢的先开始
B.用掷骰子的方法,点数大于3时小明先开始,点数小于或等于3时小红先开始
C.投掷一枚一元硬币连续掷两次,朝上的面相同时,小明先开始,则朝上的面不同时,小红先开始
D.在9张写有数字1-9的卡牌中,打乱后各自任意抽取1张,数值是单数的小明先开始,双数则是小红先开始
7.方方和圆圆用转盘做游戏,指针停在黄色区域算方方赢,停在蓝色区域算圆圆赢,停在红色区域重新转。下面三个转盘,用转盘( ),圆圆赢的可能性最大。
A. B. C.
8.扑克牌从红桃A到红桃K一共13张,王老师从这13张牌中随意抽取一张,抽到点数小于5的可能性与抽到点数大于10的可能性的大小关系是( )。
A.大于 B.小于 C.等于 D.无法判断
9.在下列情况中,( )摸出红球的可能性最大。
A.6白2红2黑 B.3蓝2白5红 C.6白3蓝1黄 D.3红4蓝5白
10.受台风天气的影响,明天我县( )下雨。
A.一定 B.不可能 C.可能
二、填空题
11.用“可能”“不可能”或“一定”填空。
(1)月亮绕着地球转。( )
(2)扔硬币时,( )正面朝上,也( )背面朝上。
(3)姐姐的年龄比妹妹小。( )
(4)今天星期三,明天( )星期四。
12.一个盒子里装有20张相同的卡片,其中有8张上面写着“八音坐唱”,3张上面写着“勒尤”,3张上面写着“高台狮灯”,6张上面写着“查白歌节”。老师打算请一位同学从中随机抽出一张作为国家级非物质文化遗产欣赏课的内容,那么抽出 的可能性最大,抽出 和 的可能性相同。
13.从数字卡片,中任意抽取两张,组成一个两位数,这个两位数是单数的可能性( ),是双数的可能性( )。
14.把8个红球和5个白球放在一个盒子里,任意摸出一球,会有( )种情况,摸出( )球的可能性大。
15.扑克牌从梅花A到梅花K一共是13张,李叔叔从中任意抽出一张牌,抽到点数小于6的可能性( )抽到点数大于9的可能性。(填“大于”“小于”或“等于”)
三、判断题
16.张开学习特别认真,平时考试总是考100分,这次期末考试也一定能考100分。( )
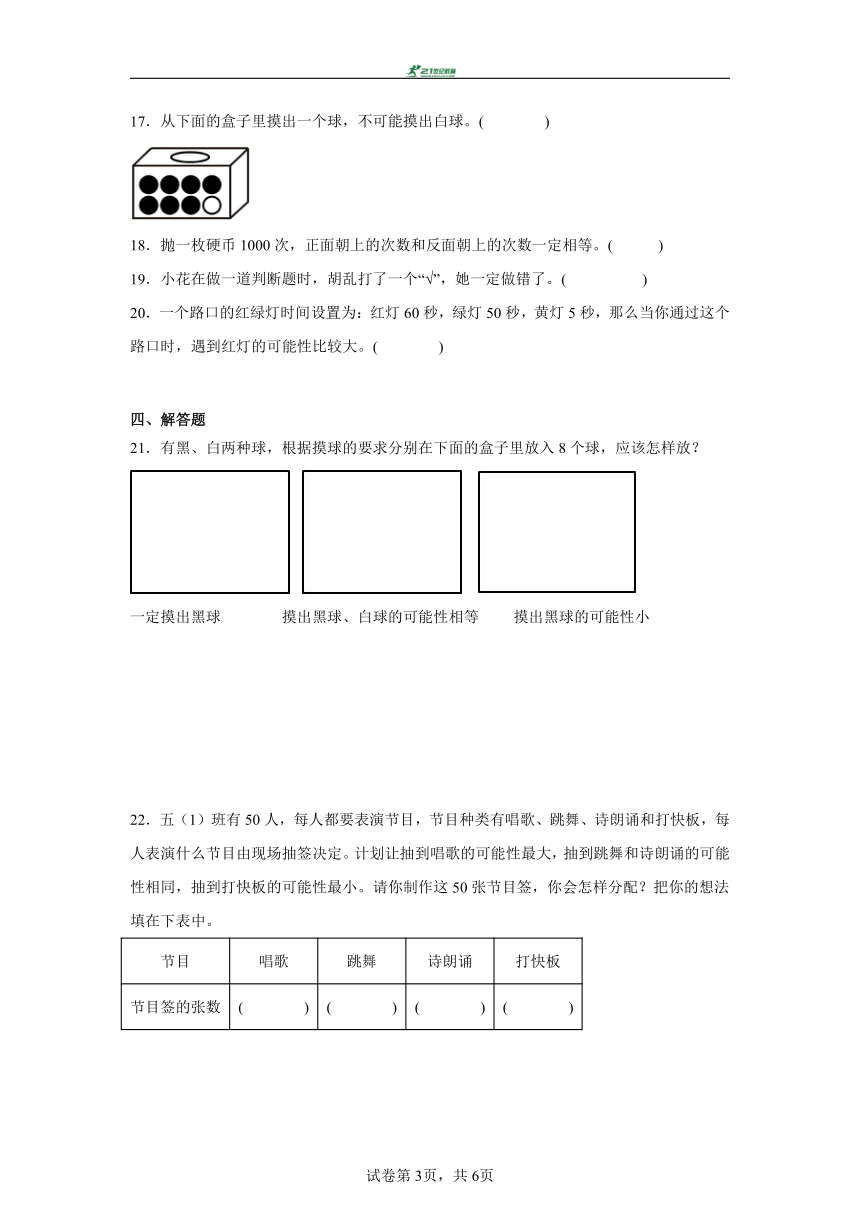
17.从下面的盒子里摸出一个球,不可能摸出白球。( )
18.抛一枚硬币1000次,正面朝上的次数和反面朝上的次数一定相等。( )
19.小花在做一道判断题时,胡乱打了一个“√”,她一定做错了。( )
20.一个路口的红绿灯时间设置为:红灯60秒,绿灯50秒,黄灯5秒,那么当你通过这个路口时,遇到红灯的可能性比较大。( )
四、解答题
21.有黑、白两种球,根据摸球的要求分别在下面的盒子里放入8个球,应该怎样放?
一定摸出黑球 摸出黑球、白球的可能性相等 摸出黑球的可能性小
22.五(1)班有50人,每人都要表演节目,节目种类有唱歌、跳舞、诗朗诵和打快板,每人表演什么节目由现场抽签决定。计划让抽到唱歌的可能性最大,抽到跳舞和诗朗诵的可能性相同,抽到打快板的可能性最小。请你制作这50张节目签,你会怎样分配?把你的想法填在下表中。
节目 唱歌 跳舞 诗朗诵 打快板
节目签的张数 ( ) ( ) ( ) ( )
23.盒子里装有15个球,分别写着1~15各数。只摸出一个球,如果摸到是双数,小刚赢,如果摸到的是单数,小强赢。
①这样约定公平吗?为什么?
②小强一定会赢吗?为什么?
③你能设计一个公平的规则吗?
24.小虎给4个小朋友写信。由于粗心,在把信纸装入信封时装错了。4个好朋友收到的都是给别人的信,小虎装错的情况共有多少种可能?
25.从下面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
26.丽丽准备用下面这7张扑克牌和明明做游戏。
丽丽:每次摸一张牌,摸到单数算我赢,摸到双数算你赢。
明明:如果这个游戏规则公平,那么我就跟你玩。
你认为这个游戏规则公平吗?为什么?
27.在举行中国象棋决赛前夕,学校公布了参加决赛的两名棋手的有关资料。
李俊 张宁
双方交战记录 5胜6负 6胜5负
在校象棋队练习成绩 15胜3负 11胜5负
(1)你认为本次象棋决赛中,谁获胜的可能性大些?说说理由。
(2)如果学校要推荐一名棋手参加区里的比赛,你认为推荐谁比较合适?简要说明理由。
28.有23枚硬币在桌上,其中10枚正面朝上.蒙住你的眼睛(你无法分清硬币正反,但可以翻转硬币),问如何操作能将硬币分成两组,让两组硬币正面朝上的一样多?简述理由.
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B A D B A B C
1.A
【分析】事件发生的可能性的大小,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。无论在什么情况下,都会发生的事件,是“一定”会发生的事件。
【详解】小明的年龄一定比他爸爸的年龄小。
故答案为:A
【点睛】具有一定生活常识即可解答本题。
2.B
【分析】理解每个成语的含义,根据可能性大小的判断方法,逐项分析各成语反映的事件发生可能性的大小,选出可能性最小的即可。
【详解】A.旭日东升,太阳从东边升起是必然事件,一定会发生;
B.守株待兔,兔子不一定会撞树,发生的可能性很小;
C.夕阳西下,太阳从西边落下是必然事件,一定会发生;
D.日月交替,太阳和月亮每天轮流转换是必然事件,一定会发生。
所以,可能性最小的是守株待兔。
故答案为:B
3.C
【分析】抛硬币只会出现正面朝上和反面朝上两种结果,每种结果朝上的可能性都为,不会受投掷的次数影响。
【详解】每次抛硬币是一个独立事件,下一次的结果不会受前一次的影响,所以可能出现投掷9次,正面朝上5次,反面4次这样的事件,但并能说明正面朝上的可能性比反面朝上的可能性大。如果抛第10次,正面、反面朝上的可能性还是一样大。
故答案为:C
【点睛】本题主要考查的是对随机事件概念的理解,解决此类问题,要学会关注身边的事物,用数学的思想和方法去分析、看待、解决问题。
4.B
【分析】判断口袋中是否有红球,需要根据摸球的次数和可能性的大小来分析。据此解答。
【详解】虽然摸了10次都没有摸到红球,但这并不意味着口袋里一定没有红球。因为仅仅摸了10次,这是一个有限的次数,有可能红球的数量很少,在这10次摸球中没有被摸到。所以,口袋中可能有红球,也可能没有红球。
故答案为:B
5.A
【分析】“一定”表示确定事件,一定会发生,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,即不可能发生的事情;盒子里有相同数量的红球和黑球,小丽从中摸出一个球,可能是红球,也可能是白球,据此解答。
【详解】根据分析可知,一个盒子里只有相同数量的红球和黑球,小丽从中摸出一个球,可能是白球。
故答案为:A
6.D
【分析】判断游戏的公平性就要看游戏双方先后顺序的可能性相同,根据可能性的大小由事件出现的次数多少决定,判断每个选项中先后顺序是否公平,来找出正确答案即可。
【详解】A.用“剪刀石头布”的猜拳方法,赢或输的可能性相同,所以确定先后顺序的方法公平;
B.点数大于3有4、5、6三种情况,点数小于或等于3有1、2、3三种情况,出现的可能性相等,所以确定先后顺序的方法公平;
C.投掷一枚一元硬币连续掷两次,有正正、反反、正反、反正四种情况,朝上的面相同有2种情况,朝上的面不同时有2种情况,所以确定先后顺序的方法公平;
D.数字1-9的卡牌中,单数的有1、3、5、7、9,双数有2、4、6、8,出现的可能性不同,所以确定先后顺序的方法不公平。
故答案为:D
7.B
【分析】根据可能性大小的判断方法,比较三个转盘中各种颜色区域的大小,哪种颜色所占的区域最大,说明指针停在这种颜色区域的可能最大;
结合游戏规则,要使圆圆赢的可能性最大,那么指针停在蓝色区域的可能性要最大,即转盘上蓝色所占的区域要最大,据此解答。
【详解】A.红色所占的区域最大,则指针停在红色区域的可能性最大,表示重新转,不符合题意;
B.蓝色所占的区域最大,则指针停在蓝色区域的可能性最大,表示圆圆赢的可能最大,符合题意;
C.三种颜色所占的区域一样大,则指针停在红、黄、蓝色区域的可能性一样大,不符合题意。
故答案为:B
【点睛】本题考查可能性的大小,结合游戏规则,判断转盘上各颜色所占区域的大小判断可能性的大小。
8.A
【分析】扑克牌从红桃A到红桃K一共13张,则点数小于5的牌有4张,大于10的牌有3张。即从13张牌中任意抽出一张牌点数小于5的可能有4张,点数大于10的可能有3张。4张大于3张,据此可得出答案。
【详解】从13张牌中任意抽出一张牌点数小于5的可能有4张,点数大于10的可能有3张。则抽到点数小于5的可能性大于抽到点数大于10的可能性。
故答案为:A
9.B
【分析】分别比较各选项中各种球的数量,哪种球的数量多,摸出哪种球的可能性就最大,据此分析。
【详解】A.6>2,摸出白球的可能性最大;
B.5>3>2,摸出红球的可能性最大;
C.6>3>1,摸出白球的可能性最大;
D.5>4>3,摸出白球的可能性最大。
3蓝2白5红摸出红球的可能性最大。
故答案为:B
10.C
【分析】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。
在任何情况下,都不会发生的事件,是“不可能”事件。
在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
【详解】受台风天气的影响,明天的天气是随机事件中的可能性事件,明天我县可能下雨。
故答案为:C
11. 一定 可能 可能 不可能 一定
【分析】事件发生的结果是可以预知的,是确定事件;事件的结果是不可预知的,是不确定事件。确定事件用“一定”“不可能”来描述,不确定事件用“可能”来描述。
【详解】(1)月亮一定绕着地球转。
(2)扔硬币时,正面可能朝上,背面可能朝上。
(3)姐姐的年龄不可能比妹妹小。
(4)今天星期三,明天一定星期四。
【点睛】本题主要考查了事件发生的确定性和不确定性,一定要做好区分。
12. 八音坐唱 勒尤 高台狮灯
【分析】当总数一定时,数量越多,则抽到的可能性越大,数量越少,则抽到的可能性越小,当数量相同时,则抽到的可能性一样,据此即可填空。
【详解】8>6>3>3
一个盒子里装有20张相同的卡片,其中有8张上面写着“八音坐唱”,3张上面写着“勒尤”,3张上面写着“高台狮灯”,6张上面写着“查白歌节”。老师打算请一位同学从中随机抽出一张作为国家级非物质文化遗产欣赏课的内容,那么抽出八音坐唱的可能性最大,抽出勒尤和高台狮灯的可能性相同。
13. 大 小
【分析】用3,6,9组成的两位数有36,39,63,69,93,96;一共有6个;找出单数的个数和双数的个数;再根据可能性大小,比较单数和双数的数量,哪种数量多可能性就大,反之,可能性就小,据此解答
【详解】3,6,9组成的两位数有36,39,63,69,93,96;
单数:39,63,69,93一共4个;
双数:36,96一共2个;
4>2,两位数是单数的可能性大,是双数的可能性小。
从数字卡片,中任意抽取两张,组成一个两位数,这个两位数是单数的可能性大,是双数的可能性小。
14. 2 红
【分析】盒子里有红球和白球2种颜色的球,任意摸出一球,可能是红球,也可能是白球,即会有2种情况;根据可能性大小:在大小形状相同的情况下,哪种球的数量最多,摸到的可能性就越大;反之,哪种球的数量最少,摸到的可能性就越小,据此解答。
【详解】盒子里有红球和白球2种颜色,任意摸出一球,会有2种情况。
8>5,摸到红球的可能性大。
把8个红球和5个白球放在一个盒子里,任意摸出一球,会有2种情况,摸出红球的可能性大。
15.大于
【分析】比较点数小于6的张数和点数大于9的张数,哪种点数张数的数量多,抽到的点数张数的可能性越大,据此解答。
【详解】扑克牌从梅花A到梅花K一共是13张,其中小于6的有:梅花A,梅花2,梅花3,梅花4,梅花5,一共有5张;
大于9的有:梅花10,梅花J,梅花Q,梅花K;一共4张;
5>4,抽到点数小于6的可能大于抽到点数大于9的可能性。
扑克牌从梅花A到梅花K一共是13张,李叔叔从中任意抽出一张牌,抽到点数小于6的可能性大于抽到点数大于9的可能性。
16.×
【分析】此题属于不确定事件,不能保证每次都考100分。
【详解】平时考试总是考100分,但不能保证这次期末考试也一定能考100分。
故答案为:×
【点睛】解决本题的关键是能够区分确定事件和不确定事件。
17.×
【分析】观察图片可知:盒子里有7个黑球,1个白球,那么从盒子里摸出一个球,有可能正好摸出白球。
【详解】通过分析可得:从上面的盒子里摸出一个球,可能摸出白球。原题说法错误。
故答案为:×
18.×
【分析】可能性是指事物发生的概率,是包括在事物之中并预示着事物发展趋势的量化指标。抛硬币,正面朝上和反面朝上的可能一样,这只是一种趋势,不能保证次数一定相同,据此判断即可。
【详解】抛一枚硬币1000次,正面朝上的次数和反面朝上的次数可能相等,本题说法错误。
故答案为:×
19.×
【分析】判断题的正确答案有两种可能性,一种是正确,一种是错误,正确和错误的可能性相等,小花可能做对了,也可能做错了,属于“可能”事件,据此解答。
【详解】根据分析可知,小花在做一道判断题时,胡乱打了一个“√”,她可能做错了,也可能做对了,并不一定做错。
原题干说法错误。
故答案为:×
【点睛】掌握用“一定”,“可能”,“不可能”等词语来描述事件发生的可能性是解答题目的关键。
20.√
【分析】哪种颜色的信号灯持续的时间长,遇到的可能性就大,反之即小,据此解答。
【详解】因为60>50>5
则当你通过这个路口时,遇到红灯的可能性比较大。原题干说法正确。
故答案为:√
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断即可。
21.见详解
【分析】要想从第一个盒子中摸出的一定是黑球,则盒子里应全是黑球;要使从第二个盒子中摸出黑球的可能性和摸出白球的可能性一样,则应使黑球的个数等于白球的个数,即黑球和白球各放入4个;要使从第三个盒子中摸出黑球的可能性小,则应使白球的个数多于黑球的个数。据此解答。
【详解】根据分析得,
第一个盒子放入8个黑球;
第二个盒子放入4个黑球和4个白球;
第三个盒子放入3个黑球和5个白球。(答案不唯一)
如下图所示:
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
22. 16 12 12 10
【分析】抽到唱歌的可能性最大,就是唱歌的节目签的张数最多,抽到跳舞和诗朗诵的可能性相等,贝两种签的张数一样多,抽到打快板的可能性最小,这种节目签的张数最少,使四种节目签的张数和为50张即可。
【详解】16+12+12+10=50(张)
答:我会这样分配节目签:唱歌的节目签有16张,跳舞和诗朗诵的节目签各有12张,打快板的节目签有10张。(答案不唯一)
填表如下:
节目 唱歌 跳舞 诗朗诵 打快板
节目签的张数 16 12 12 10
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
23.①不公平;双数小于单数,小强获胜的可能性大
②见详解
③见详解
【分析】①判断游戏是否公平,主要是看两人获胜的可能性是不是一样大,分别写出1~15中的双数和单数,如果单数和双数一样多,说明这样的约定公平,如果单数和双数不一样多,则游戏不公平;
②个数多的赢的可能性大,但不一定会赢,个数少的也可能会赢;
③只要获胜的可能性一样大,游戏就公平,据此解答即可。(答案不唯一)
【详解】①1~15中的双数有:2、4、6、8、10、12、14共7个;单数有:1、3、5、7、9、11、13、15共8个,7<8,双数小于单数,小强获胜的可能性大写,所以游戏约定不公平;
②双数小于单数,只能说明小强获胜的可能性大些,但不能保证小强会赢;
③设计公平游戏如下:抓到1,2,3小刚赢,抓到4,5,6小强赢。
24.9种
【分析】把4封信编号:1,2,3,4;把小朋友编号,友1,友2,友3,友4,并假定1号信是给友1写的,2号信是给友2写的,3号信是给友3写的,4号信是给友4写的。通过画图的方式,排列出错装的情况,再计算。
【详解】
3×3=9(种)
答:小虎装错的情况共有9种可能。
25.可能是红色、蓝色、黄色;红色可能性最大;黄色可能性最小
【分析】根据题意,盒子里有三种颜色的棋子,那么任意摸出1个棋子,就有可能摸到这三种颜色中的任何一个,所以三种颜色的棋子都有可能摸到。
根据可能性大小的判断方法,比较盒子里三种颜色棋子的数量多少,数量最多的,摸到的可能性最大;数量最小的,摸到的可能性最小。
【详解】因为盒子里有红、蓝、黄三种颜色的棋子,所以从盒子里摸出一个棋子,可能是红色,可能是蓝色,还可能是黄色。
红色棋子有7个,蓝色棋子有4个,黄色棋子有1个;
7>4>1
红色棋子最多,摸到的可能性最大;黄色棋子最少,摸到的可能性最小。
答:从盒子里摸出一个棋子,可能是红色、蓝色、黄色。摸出红色棋子的可能性最大,摸出黄色棋子的可能性最小。
【点睛】本题考查可能性的知识,根据数量的多少判断可能性的大小。
26.不公平;摸到单数的可能性大于摸到双数的可能性
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。要使游戏公平,则两人赢的可能性要相等;已知1、3、5、7是单数,共4个;2、4、6是双数,共3个;摸到单数的可能性大于摸到双数的可能性,据此解答。
【详解】1、3、5、7是单数,共4个;2、4、6是双数,共3个;
4>3
摸到单数的可能性大于摸到双数的可能性,所以丽丽赢的可能性大于明明赢的可能性。游戏不公平。
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
27.(1)张宁获胜的可能性大些。因为李俊获胜的可能性是,张宁获胜的可能性是,。
(2)我认为推荐李俊去参加比较合适。他与其他学生比赛的胜率更大一些。
【分析】(1)通过李俊与张宁的双方交战记录,可以得出两人共比赛了5+6=11(局),李俊获胜的成绩是,张宁获胜的成绩是,。
(2)李俊在练习的过程中,15胜3负,胜利的可能性是18局比赛里面有15局是胜利的,也就是胜率约是0.83;
而张宁在练习的过程中,11胜5负,胜利的可能性16局比赛里面有11局是胜利的,也就是胜率约是0.69;
则李俊的获胜的可能性比较大。
【详解】(1)李俊获胜的可能性:
张宁获胜的可能性:
答:张宁获胜的可能性大些。
(2 )15÷(15+3)
=15÷18
≈0.83
11÷(11+5)
=11÷16
≈0.69
0.85>0.69
答:我认为推荐李俊去参加比较合适。他与其他学生比赛的胜率更大一些。
28.将这23枚硬币分成10个、13个两组,然后将10个一组的所有硬币翻转就可以了,这时两堆正面朝上的硬币个数就一样了.
原理:假设13个一组的有a个正面朝上的,那么10个一堆的则有(10﹣a)个正面朝上的.这时把10个一组的全部翻转,正面的变成反面的,反面的变成正面的,则正面朝上的有10﹣(10﹣a)个,即a个.所以13个一组的正面朝上的有a个,10个一组的正面朝上的也有a个,即两边正面朝上的个数相同.
【解析】略
答案第11页,共22页
答案第11页,共22页
一、选择题
1.小明的年龄( )比他爸爸的年龄小。
A.一定 B.可能 C.不可能
2.下列成语反映的事件中,可能性最小的是( )。
A.旭日东升 B.守株待兔 C.夕阳西下 D.日月交替
3.明明抛一枚硬币,共抛了9次,其中正面朝上5次,反面4次。如果抛第10次,则( )。
A.正面朝上的可能性大 B.反面朝上的可能性大
C.正面、反面朝上的可能性一样大 D.无法判断
4.从一个口袋里摸球,摸了10次也没有摸到红球,说明口袋里( )红球。
A.一定没有 B.可能没有 C.一定有
5.一个盒子里只有相同数量的红球和黑球,小丽从中摸出一个球,( )是白球。
A.可能 B.不可能 C.一定
6.小明和小红玩飞行棋,下面的确定先后顺序的方法不公平的是( )。
A.用“剪刀石头布”的猜拳方法,赢的先开始
B.用掷骰子的方法,点数大于3时小明先开始,点数小于或等于3时小红先开始
C.投掷一枚一元硬币连续掷两次,朝上的面相同时,小明先开始,则朝上的面不同时,小红先开始
D.在9张写有数字1-9的卡牌中,打乱后各自任意抽取1张,数值是单数的小明先开始,双数则是小红先开始
7.方方和圆圆用转盘做游戏,指针停在黄色区域算方方赢,停在蓝色区域算圆圆赢,停在红色区域重新转。下面三个转盘,用转盘( ),圆圆赢的可能性最大。
A. B. C.
8.扑克牌从红桃A到红桃K一共13张,王老师从这13张牌中随意抽取一张,抽到点数小于5的可能性与抽到点数大于10的可能性的大小关系是( )。
A.大于 B.小于 C.等于 D.无法判断
9.在下列情况中,( )摸出红球的可能性最大。
A.6白2红2黑 B.3蓝2白5红 C.6白3蓝1黄 D.3红4蓝5白
10.受台风天气的影响,明天我县( )下雨。
A.一定 B.不可能 C.可能
二、填空题
11.用“可能”“不可能”或“一定”填空。
(1)月亮绕着地球转。( )
(2)扔硬币时,( )正面朝上,也( )背面朝上。
(3)姐姐的年龄比妹妹小。( )
(4)今天星期三,明天( )星期四。
12.一个盒子里装有20张相同的卡片,其中有8张上面写着“八音坐唱”,3张上面写着“勒尤”,3张上面写着“高台狮灯”,6张上面写着“查白歌节”。老师打算请一位同学从中随机抽出一张作为国家级非物质文化遗产欣赏课的内容,那么抽出 的可能性最大,抽出 和 的可能性相同。
13.从数字卡片,中任意抽取两张,组成一个两位数,这个两位数是单数的可能性( ),是双数的可能性( )。
14.把8个红球和5个白球放在一个盒子里,任意摸出一球,会有( )种情况,摸出( )球的可能性大。
15.扑克牌从梅花A到梅花K一共是13张,李叔叔从中任意抽出一张牌,抽到点数小于6的可能性( )抽到点数大于9的可能性。(填“大于”“小于”或“等于”)
三、判断题
16.张开学习特别认真,平时考试总是考100分,这次期末考试也一定能考100分。( )
17.从下面的盒子里摸出一个球,不可能摸出白球。( )
18.抛一枚硬币1000次,正面朝上的次数和反面朝上的次数一定相等。( )
19.小花在做一道判断题时,胡乱打了一个“√”,她一定做错了。( )
20.一个路口的红绿灯时间设置为:红灯60秒,绿灯50秒,黄灯5秒,那么当你通过这个路口时,遇到红灯的可能性比较大。( )
四、解答题
21.有黑、白两种球,根据摸球的要求分别在下面的盒子里放入8个球,应该怎样放?
一定摸出黑球 摸出黑球、白球的可能性相等 摸出黑球的可能性小
22.五(1)班有50人,每人都要表演节目,节目种类有唱歌、跳舞、诗朗诵和打快板,每人表演什么节目由现场抽签决定。计划让抽到唱歌的可能性最大,抽到跳舞和诗朗诵的可能性相同,抽到打快板的可能性最小。请你制作这50张节目签,你会怎样分配?把你的想法填在下表中。
节目 唱歌 跳舞 诗朗诵 打快板
节目签的张数 ( ) ( ) ( ) ( )
23.盒子里装有15个球,分别写着1~15各数。只摸出一个球,如果摸到是双数,小刚赢,如果摸到的是单数,小强赢。
①这样约定公平吗?为什么?
②小强一定会赢吗?为什么?
③你能设计一个公平的规则吗?
24.小虎给4个小朋友写信。由于粗心,在把信纸装入信封时装错了。4个好朋友收到的都是给别人的信,小虎装错的情况共有多少种可能?
25.从下面的盒子里摸出一个棋子,可能是什么颜色?猜一猜:摸出哪种颜色棋子的可能性最大?摸出哪种颜色棋子的可能性最小?
26.丽丽准备用下面这7张扑克牌和明明做游戏。
丽丽:每次摸一张牌,摸到单数算我赢,摸到双数算你赢。
明明:如果这个游戏规则公平,那么我就跟你玩。
你认为这个游戏规则公平吗?为什么?
27.在举行中国象棋决赛前夕,学校公布了参加决赛的两名棋手的有关资料。
李俊 张宁
双方交战记录 5胜6负 6胜5负
在校象棋队练习成绩 15胜3负 11胜5负
(1)你认为本次象棋决赛中,谁获胜的可能性大些?说说理由。
(2)如果学校要推荐一名棋手参加区里的比赛,你认为推荐谁比较合适?简要说明理由。
28.有23枚硬币在桌上,其中10枚正面朝上.蒙住你的眼睛(你无法分清硬币正反,但可以翻转硬币),问如何操作能将硬币分成两组,让两组硬币正面朝上的一样多?简述理由.
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B A D B A B C
1.A
【分析】事件发生的可能性的大小,对事件发生的可能大小,可以用“一定”“经常”“偶尔”“可能”“不可能”等词语来描述。无论在什么情况下,都会发生的事件,是“一定”会发生的事件。
【详解】小明的年龄一定比他爸爸的年龄小。
故答案为:A
【点睛】具有一定生活常识即可解答本题。
2.B
【分析】理解每个成语的含义,根据可能性大小的判断方法,逐项分析各成语反映的事件发生可能性的大小,选出可能性最小的即可。
【详解】A.旭日东升,太阳从东边升起是必然事件,一定会发生;
B.守株待兔,兔子不一定会撞树,发生的可能性很小;
C.夕阳西下,太阳从西边落下是必然事件,一定会发生;
D.日月交替,太阳和月亮每天轮流转换是必然事件,一定会发生。
所以,可能性最小的是守株待兔。
故答案为:B
3.C
【分析】抛硬币只会出现正面朝上和反面朝上两种结果,每种结果朝上的可能性都为,不会受投掷的次数影响。
【详解】每次抛硬币是一个独立事件,下一次的结果不会受前一次的影响,所以可能出现投掷9次,正面朝上5次,反面4次这样的事件,但并能说明正面朝上的可能性比反面朝上的可能性大。如果抛第10次,正面、反面朝上的可能性还是一样大。
故答案为:C
【点睛】本题主要考查的是对随机事件概念的理解,解决此类问题,要学会关注身边的事物,用数学的思想和方法去分析、看待、解决问题。
4.B
【分析】判断口袋中是否有红球,需要根据摸球的次数和可能性的大小来分析。据此解答。
【详解】虽然摸了10次都没有摸到红球,但这并不意味着口袋里一定没有红球。因为仅仅摸了10次,这是一个有限的次数,有可能红球的数量很少,在这10次摸球中没有被摸到。所以,口袋中可能有红球,也可能没有红球。
故答案为:B
5.A
【分析】“一定”表示确定事件,一定会发生,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,即不可能发生的事情;盒子里有相同数量的红球和黑球,小丽从中摸出一个球,可能是红球,也可能是白球,据此解答。
【详解】根据分析可知,一个盒子里只有相同数量的红球和黑球,小丽从中摸出一个球,可能是白球。
故答案为:A
6.D
【分析】判断游戏的公平性就要看游戏双方先后顺序的可能性相同,根据可能性的大小由事件出现的次数多少决定,判断每个选项中先后顺序是否公平,来找出正确答案即可。
【详解】A.用“剪刀石头布”的猜拳方法,赢或输的可能性相同,所以确定先后顺序的方法公平;
B.点数大于3有4、5、6三种情况,点数小于或等于3有1、2、3三种情况,出现的可能性相等,所以确定先后顺序的方法公平;
C.投掷一枚一元硬币连续掷两次,有正正、反反、正反、反正四种情况,朝上的面相同有2种情况,朝上的面不同时有2种情况,所以确定先后顺序的方法公平;
D.数字1-9的卡牌中,单数的有1、3、5、7、9,双数有2、4、6、8,出现的可能性不同,所以确定先后顺序的方法不公平。
故答案为:D
7.B
【分析】根据可能性大小的判断方法,比较三个转盘中各种颜色区域的大小,哪种颜色所占的区域最大,说明指针停在这种颜色区域的可能最大;
结合游戏规则,要使圆圆赢的可能性最大,那么指针停在蓝色区域的可能性要最大,即转盘上蓝色所占的区域要最大,据此解答。
【详解】A.红色所占的区域最大,则指针停在红色区域的可能性最大,表示重新转,不符合题意;
B.蓝色所占的区域最大,则指针停在蓝色区域的可能性最大,表示圆圆赢的可能最大,符合题意;
C.三种颜色所占的区域一样大,则指针停在红、黄、蓝色区域的可能性一样大,不符合题意。
故答案为:B
【点睛】本题考查可能性的大小,结合游戏规则,判断转盘上各颜色所占区域的大小判断可能性的大小。
8.A
【分析】扑克牌从红桃A到红桃K一共13张,则点数小于5的牌有4张,大于10的牌有3张。即从13张牌中任意抽出一张牌点数小于5的可能有4张,点数大于10的可能有3张。4张大于3张,据此可得出答案。
【详解】从13张牌中任意抽出一张牌点数小于5的可能有4张,点数大于10的可能有3张。则抽到点数小于5的可能性大于抽到点数大于10的可能性。
故答案为:A
9.B
【分析】分别比较各选项中各种球的数量,哪种球的数量多,摸出哪种球的可能性就最大,据此分析。
【详解】A.6>2,摸出白球的可能性最大;
B.5>3>2,摸出红球的可能性最大;
C.6>3>1,摸出白球的可能性最大;
D.5>4>3,摸出白球的可能性最大。
3蓝2白5红摸出红球的可能性最大。
故答案为:B
10.C
【分析】无论在什么情况下,都会发生的事件,是“一定”会发生的事件。
在任何情况下,都不会发生的事件,是“不可能”事件。
在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。
【详解】受台风天气的影响,明天的天气是随机事件中的可能性事件,明天我县可能下雨。
故答案为:C
11. 一定 可能 可能 不可能 一定
【分析】事件发生的结果是可以预知的,是确定事件;事件的结果是不可预知的,是不确定事件。确定事件用“一定”“不可能”来描述,不确定事件用“可能”来描述。
【详解】(1)月亮一定绕着地球转。
(2)扔硬币时,正面可能朝上,背面可能朝上。
(3)姐姐的年龄不可能比妹妹小。
(4)今天星期三,明天一定星期四。
【点睛】本题主要考查了事件发生的确定性和不确定性,一定要做好区分。
12. 八音坐唱 勒尤 高台狮灯
【分析】当总数一定时,数量越多,则抽到的可能性越大,数量越少,则抽到的可能性越小,当数量相同时,则抽到的可能性一样,据此即可填空。
【详解】8>6>3>3
一个盒子里装有20张相同的卡片,其中有8张上面写着“八音坐唱”,3张上面写着“勒尤”,3张上面写着“高台狮灯”,6张上面写着“查白歌节”。老师打算请一位同学从中随机抽出一张作为国家级非物质文化遗产欣赏课的内容,那么抽出八音坐唱的可能性最大,抽出勒尤和高台狮灯的可能性相同。
13. 大 小
【分析】用3,6,9组成的两位数有36,39,63,69,93,96;一共有6个;找出单数的个数和双数的个数;再根据可能性大小,比较单数和双数的数量,哪种数量多可能性就大,反之,可能性就小,据此解答
【详解】3,6,9组成的两位数有36,39,63,69,93,96;
单数:39,63,69,93一共4个;
双数:36,96一共2个;
4>2,两位数是单数的可能性大,是双数的可能性小。
从数字卡片,中任意抽取两张,组成一个两位数,这个两位数是单数的可能性大,是双数的可能性小。
14. 2 红
【分析】盒子里有红球和白球2种颜色的球,任意摸出一球,可能是红球,也可能是白球,即会有2种情况;根据可能性大小:在大小形状相同的情况下,哪种球的数量最多,摸到的可能性就越大;反之,哪种球的数量最少,摸到的可能性就越小,据此解答。
【详解】盒子里有红球和白球2种颜色,任意摸出一球,会有2种情况。
8>5,摸到红球的可能性大。
把8个红球和5个白球放在一个盒子里,任意摸出一球,会有2种情况,摸出红球的可能性大。
15.大于
【分析】比较点数小于6的张数和点数大于9的张数,哪种点数张数的数量多,抽到的点数张数的可能性越大,据此解答。
【详解】扑克牌从梅花A到梅花K一共是13张,其中小于6的有:梅花A,梅花2,梅花3,梅花4,梅花5,一共有5张;
大于9的有:梅花10,梅花J,梅花Q,梅花K;一共4张;
5>4,抽到点数小于6的可能大于抽到点数大于9的可能性。
扑克牌从梅花A到梅花K一共是13张,李叔叔从中任意抽出一张牌,抽到点数小于6的可能性大于抽到点数大于9的可能性。
16.×
【分析】此题属于不确定事件,不能保证每次都考100分。
【详解】平时考试总是考100分,但不能保证这次期末考试也一定能考100分。
故答案为:×
【点睛】解决本题的关键是能够区分确定事件和不确定事件。
17.×
【分析】观察图片可知:盒子里有7个黑球,1个白球,那么从盒子里摸出一个球,有可能正好摸出白球。
【详解】通过分析可得:从上面的盒子里摸出一个球,可能摸出白球。原题说法错误。
故答案为:×
18.×
【分析】可能性是指事物发生的概率,是包括在事物之中并预示着事物发展趋势的量化指标。抛硬币,正面朝上和反面朝上的可能一样,这只是一种趋势,不能保证次数一定相同,据此判断即可。
【详解】抛一枚硬币1000次,正面朝上的次数和反面朝上的次数可能相等,本题说法错误。
故答案为:×
19.×
【分析】判断题的正确答案有两种可能性,一种是正确,一种是错误,正确和错误的可能性相等,小花可能做对了,也可能做错了,属于“可能”事件,据此解答。
【详解】根据分析可知,小花在做一道判断题时,胡乱打了一个“√”,她可能做错了,也可能做对了,并不一定做错。
原题干说法错误。
故答案为:×
【点睛】掌握用“一定”,“可能”,“不可能”等词语来描述事件发生的可能性是解答题目的关键。
20.√
【分析】哪种颜色的信号灯持续的时间长,遇到的可能性就大,反之即小,据此解答。
【详解】因为60>50>5
则当你通过这个路口时,遇到红灯的可能性比较大。原题干说法正确。
故答案为:√
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断即可。
21.见详解
【分析】要想从第一个盒子中摸出的一定是黑球,则盒子里应全是黑球;要使从第二个盒子中摸出黑球的可能性和摸出白球的可能性一样,则应使黑球的个数等于白球的个数,即黑球和白球各放入4个;要使从第三个盒子中摸出黑球的可能性小,则应使白球的个数多于黑球的个数。据此解答。
【详解】根据分析得,
第一个盒子放入8个黑球;
第二个盒子放入4个黑球和4个白球;
第三个盒子放入3个黑球和5个白球。(答案不唯一)
如下图所示:
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
22. 16 12 12 10
【分析】抽到唱歌的可能性最大,就是唱歌的节目签的张数最多,抽到跳舞和诗朗诵的可能性相等,贝两种签的张数一样多,抽到打快板的可能性最小,这种节目签的张数最少,使四种节目签的张数和为50张即可。
【详解】16+12+12+10=50(张)
答:我会这样分配节目签:唱歌的节目签有16张,跳舞和诗朗诵的节目签各有12张,打快板的节目签有10张。(答案不唯一)
填表如下:
节目 唱歌 跳舞 诗朗诵 打快板
节目签的张数 16 12 12 10
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
23.①不公平;双数小于单数,小强获胜的可能性大
②见详解
③见详解
【分析】①判断游戏是否公平,主要是看两人获胜的可能性是不是一样大,分别写出1~15中的双数和单数,如果单数和双数一样多,说明这样的约定公平,如果单数和双数不一样多,则游戏不公平;
②个数多的赢的可能性大,但不一定会赢,个数少的也可能会赢;
③只要获胜的可能性一样大,游戏就公平,据此解答即可。(答案不唯一)
【详解】①1~15中的双数有:2、4、6、8、10、12、14共7个;单数有:1、3、5、7、9、11、13、15共8个,7<8,双数小于单数,小强获胜的可能性大写,所以游戏约定不公平;
②双数小于单数,只能说明小强获胜的可能性大些,但不能保证小强会赢;
③设计公平游戏如下:抓到1,2,3小刚赢,抓到4,5,6小强赢。
24.9种
【分析】把4封信编号:1,2,3,4;把小朋友编号,友1,友2,友3,友4,并假定1号信是给友1写的,2号信是给友2写的,3号信是给友3写的,4号信是给友4写的。通过画图的方式,排列出错装的情况,再计算。
【详解】
3×3=9(种)
答:小虎装错的情况共有9种可能。
25.可能是红色、蓝色、黄色;红色可能性最大;黄色可能性最小
【分析】根据题意,盒子里有三种颜色的棋子,那么任意摸出1个棋子,就有可能摸到这三种颜色中的任何一个,所以三种颜色的棋子都有可能摸到。
根据可能性大小的判断方法,比较盒子里三种颜色棋子的数量多少,数量最多的,摸到的可能性最大;数量最小的,摸到的可能性最小。
【详解】因为盒子里有红、蓝、黄三种颜色的棋子,所以从盒子里摸出一个棋子,可能是红色,可能是蓝色,还可能是黄色。
红色棋子有7个,蓝色棋子有4个,黄色棋子有1个;
7>4>1
红色棋子最多,摸到的可能性最大;黄色棋子最少,摸到的可能性最小。
答:从盒子里摸出一个棋子,可能是红色、蓝色、黄色。摸出红色棋子的可能性最大,摸出黄色棋子的可能性最小。
【点睛】本题考查可能性的知识,根据数量的多少判断可能性的大小。
26.不公平;摸到单数的可能性大于摸到双数的可能性
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。要使游戏公平,则两人赢的可能性要相等;已知1、3、5、7是单数,共4个;2、4、6是双数,共3个;摸到单数的可能性大于摸到双数的可能性,据此解答。
【详解】1、3、5、7是单数,共4个;2、4、6是双数,共3个;
4>3
摸到单数的可能性大于摸到双数的可能性,所以丽丽赢的可能性大于明明赢的可能性。游戏不公平。
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
27.(1)张宁获胜的可能性大些。因为李俊获胜的可能性是,张宁获胜的可能性是,。
(2)我认为推荐李俊去参加比较合适。他与其他学生比赛的胜率更大一些。
【分析】(1)通过李俊与张宁的双方交战记录,可以得出两人共比赛了5+6=11(局),李俊获胜的成绩是,张宁获胜的成绩是,。
(2)李俊在练习的过程中,15胜3负,胜利的可能性是18局比赛里面有15局是胜利的,也就是胜率约是0.83;
而张宁在练习的过程中,11胜5负,胜利的可能性16局比赛里面有11局是胜利的,也就是胜率约是0.69;
则李俊的获胜的可能性比较大。
【详解】(1)李俊获胜的可能性:
张宁获胜的可能性:
答:张宁获胜的可能性大些。
(2 )15÷(15+3)
=15÷18
≈0.83
11÷(11+5)
=11÷16
≈0.69
0.85>0.69
答:我认为推荐李俊去参加比较合适。他与其他学生比赛的胜率更大一些。
28.将这23枚硬币分成10个、13个两组,然后将10个一组的所有硬币翻转就可以了,这时两堆正面朝上的硬币个数就一样了.
原理:假设13个一组的有a个正面朝上的,那么10个一堆的则有(10﹣a)个正面朝上的.这时把10个一组的全部翻转,正面的变成反面的,反面的变成正面的,则正面朝上的有10﹣(10﹣a)个,即a个.所以13个一组的正面朝上的有a个,10个一组的正面朝上的也有a个,即两边正面朝上的个数相同.
【解析】略
答案第11页,共22页
答案第11页,共22页
