2025届高考物理一轮复习导学案:万有引力定律(第1课时)
文档属性
| 名称 | 2025届高考物理一轮复习导学案:万有引力定律(第1课时) |
|
|
| 格式 | docx | ||
| 文件大小 | 333.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-01 00:00:00 | ||
图片预览


文档简介
万有引力定律及应用 第1课时
-----导学思练测
学习目标:1.了解开普勒三定律内容,会用开普勒第三定律进行相关计算。 2.理解万有引力定律的内容,知道适用范围。 3.掌握计算天体质量和密度的方法。
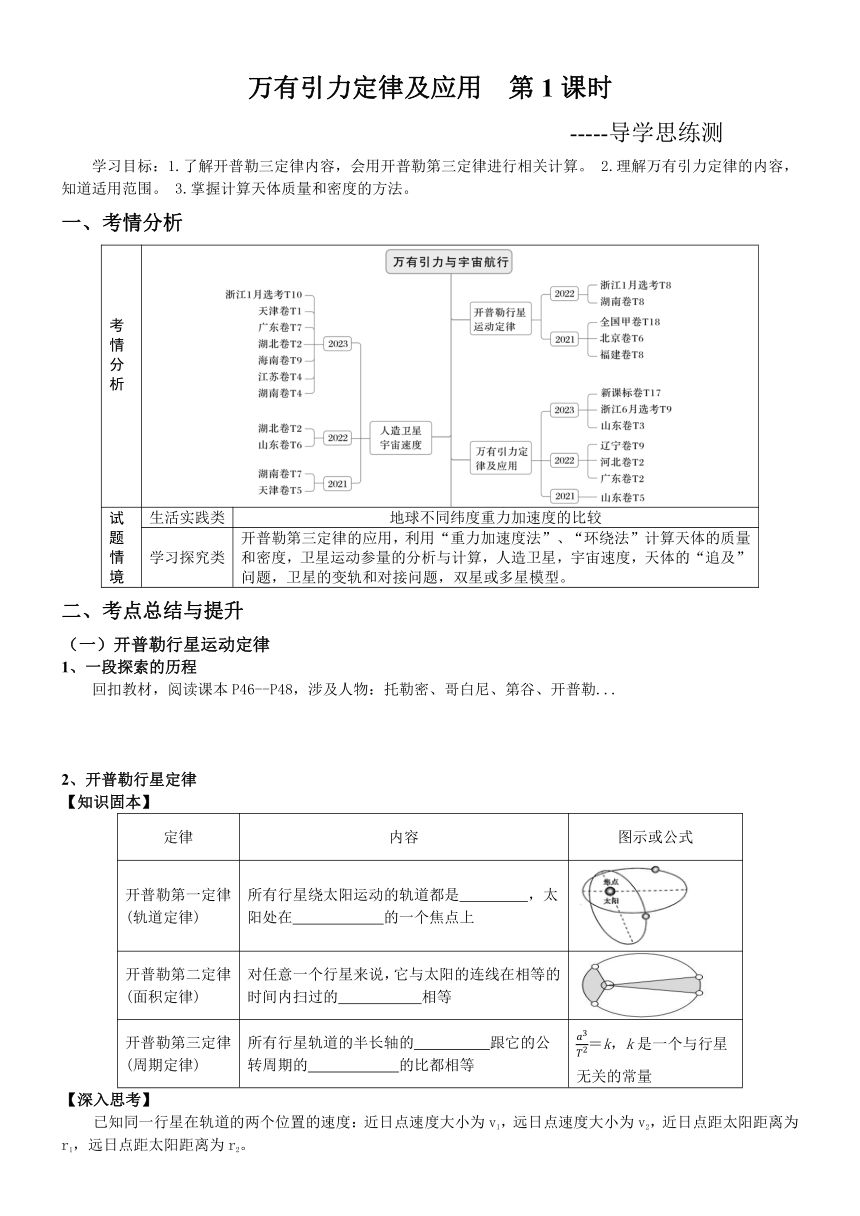
考情分析
考情分析
试题情境 生活实践类 地球不同纬度重力加速度的比较
学习探究类 开普勒第三定律的应用,利用“重力加速度法”、“环绕法”计算天体的质量和密度,卫星运动参量的分析与计算,人造卫星,宇宙速度,天体的“追及”问题,卫星的变轨和对接问题,双星或多星模型。
考点总结与提升
开普勒行星运动定律
一段探索的历程
回扣教材,阅读课本P46--P48,涉及人物:托勒密、哥白尼、第谷、开普勒...
开普勒行星定律
【知识固本】
定律 内容 图示或公式
开普勒第一定律(轨道定律) 所有行星绕太阳运动的轨道都是 ,太阳处在 的一个焦点上
开普勒第二定律(面积定律) 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的 相等
开普勒第三定律(周期定律) 所有行星轨道的半长轴的 跟它的公转周期的 的比都相等 =k,k是一个与行星无关的常量
【深入思考】
已知同一行星在轨道的两个位置的速度:近日点速度大小为v1,远日点速度大小为v2,近日点距太阳距离为r1,远日点距太阳距离为r2。
(1)v1与v2大小什么关系?
(2)试推导r1v1=v2r2
【考向洞察】
近似计算可以使题目更加简单!
【知识提升】
①行星运动 近似圆 处理。
②开普勒行星运动定律不仅适用于行星绕太阳运转,对于卫星绕行星运转,也遵循类似的运动规律。
③比例系数k与 有关,与行星或卫星质量无关,是个常量,但不是恒量,在不同的星系中,k值 。
万有引力定律
【知识固本】
万有引力定律的内容:
自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与 成正比、与它们之间 成反比。即F= ,G为引力常量,通常取G=6.67×10-11N·m2/kg2,由物理学家卡文迪什测定。
【典型例题】1、有一质量为M、半径为R、密度均匀的球体,在距离球心O为2R的地方有一质量为m的质点。现从球体中挖去半径为0.5R的小球体,如图所示,引力常量为G,则剩余部分对m的万有引力为( )
A. B. C. D.
“挖补法”求解万有引力
【知识提升】
万有引力定律的适用条件
①公式适用于 间的相互作用,当两个物体间的距离远大于物体本身的大小时,物体可视为质点。
②质量分布均匀的球体可视为质点,r是两 间的距离。
【典型例题】2、(2024·广东广州高三期中)2020年9月,我国明确提出2030年“碳达峰”与2060年“碳中和”目标。人类社会的快速进步使得碳排放量不断增加,这导致温室效应加剧,地球南北两极的生态环境遭到一定的破坏。一头质量为m的北极熊在失去家园后,被运送到了位于赤道上的北极熊馆加以照料,它在北极和馆内的重力差为ΔF。已知地球自转周期为T。根据以上信息,可求出地球的半径为( )
A. B. C. D.
【知识提升】
自转模型
(1)万有引力与重力的关系
地球对物体的万有引力F表现为两个效果:一是重力mg,二是提供物体随地球自转的向心力F向,如图所示。
①在赤道上:G=
②在两极上:G=
③在一般位置:万有引力G等于重力mg与向心力F向的矢量和。
越靠近南北两极g值 ,由于物体随地球自转所需的向心力较小,常认为万有引力近似等于重力。
(2)重力的方向:①赤道与两极指向 ;②其它位置与水平面垂直或竖直向下,但不指向 。
【深入思考】
两极和赤道上的重力加速度如何表示?天上和地下呢?
地下 地面 天上
两极或不计自转 赤道
g= g= g= -Rω自2 g=
【典型例题】3、近几年来,我国生产的“蛟龙号”下潜突破7 000 m大关,我国的北斗导航系统也进入紧密的组网阶段。已知质量分布均匀的球壳对壳内任一质点的万有引力为零,将地球看成半径为R、质量分布均匀的球体,北斗导航系统中的一颗卫星的轨道距离地面的高度为h,“蛟龙号”下潜的深度为d,则该卫星所在处的重力加速度与“蛟龙号”所在处的重力加速度的大小之比为( )
A. B. C. D.
【知识提升】
球体内部万有引力的两个有用推论
(1)推论1:在匀质球壳的空腔内任意位置处,质点受到球壳的万有引力的合力为零,即ΣF引=0.
(2)推论2:在匀质球体内部距离球心r处的质点(m)受到的万有引力等于球体内半径为r的同心球体(M′)对其的万有引力,即F=G。
【考向洞察】
天体质量和密度的计算
【知识固本】
计算中心天体的质量和密度
“一个中心、两个基本点”——需要已知量r、T(或ω、v);g、R
原理 “天上”环绕法 “地上”黄金代换法
万有引力提供向心力: == 万有引力等于重力:
质量 M= = = M=
密度 ρ= = = ρ=
【典型例题】4、我国是第三个对火星探测并将探测器着陆火星的国家,探测器在环绕火星表面飞行时周期是T。火星表面气体非常稀薄可近似认为真空,在火星表面附近以初速度v0水平抛出一个物体,测得抛出点距火星表面高度为h,落到火星表面时物体的水平位移为x,已知引力常量为G,下列说法正确的是( )
A.火星表面重力加速度大小是 B.火星的半径是
C.火星的质量是 D.火星的密度是
【知识提升】
1.只能计算出中心天体的质量和密度。
2.若卫星绕天体表面运行,可认为轨道半径r等于天体半径R,则天体密度ρ=
【考向洞察】
【课堂小结】
利用3-5分钟时间,对本节课学习的内容进行总结梳理
【达标检测】
1.(2024·江苏南京模拟)某行星绕太阳运动的轨道如图所示,则以下说法正确的是( )
A.该行星在a点的向心加速度比在b、c两点的都大
B.该行星在a点的速度比在b、c两点的速度都更小
C.行星与太阳的连线在相等时间内扫过的面积是不相等的
D.行星绕太阳做匀速圆周运动,太阳在圆心上
2.某类地天体可视为质量分布均匀的球体,由于自转的原因,其表面“赤道”处的重力加速度为g1,“极点”处的重力加速度为g2,若已知自转周期为T,则该天体的半径为( )
A. B. C. D.
3.2022年8月10日,我国在太原卫星发射中心用长征六号运载火箭成功将“吉林一号”组网星中的16颗卫星发射升空,卫星顺利进入预定的环绕地球运动轨道,发射任务取得圆满成功。这16颗卫星的轨道平面各异,高度不同,通过测量发现,它们的轨道半径的三次方与运动周期的二次方成正比,且比例系数为p。已知引力常量为G,由此可知地球的质量为( )
A. B. C. D.
4. 某行星周围的卫星绕其做圆周运动的轨道半径r与运行周期T的关系如图4所示。行星的半径为R0,引力常量为G,图中a、b为已知量。下列说法正确的是( )
A.绕该行星表面运行卫星的周期为 B.该行星的质量为
C.该行星的密度为 D.该行星表面的重力加速度为
-----导学思练测
学习目标:1.了解开普勒三定律内容,会用开普勒第三定律进行相关计算。 2.理解万有引力定律的内容,知道适用范围。 3.掌握计算天体质量和密度的方法。
考情分析
考情分析
试题情境 生活实践类 地球不同纬度重力加速度的比较
学习探究类 开普勒第三定律的应用,利用“重力加速度法”、“环绕法”计算天体的质量和密度,卫星运动参量的分析与计算,人造卫星,宇宙速度,天体的“追及”问题,卫星的变轨和对接问题,双星或多星模型。
考点总结与提升
开普勒行星运动定律
一段探索的历程
回扣教材,阅读课本P46--P48,涉及人物:托勒密、哥白尼、第谷、开普勒...
开普勒行星定律
【知识固本】
定律 内容 图示或公式
开普勒第一定律(轨道定律) 所有行星绕太阳运动的轨道都是 ,太阳处在 的一个焦点上
开普勒第二定律(面积定律) 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的 相等
开普勒第三定律(周期定律) 所有行星轨道的半长轴的 跟它的公转周期的 的比都相等 =k,k是一个与行星无关的常量
【深入思考】
已知同一行星在轨道的两个位置的速度:近日点速度大小为v1,远日点速度大小为v2,近日点距太阳距离为r1,远日点距太阳距离为r2。
(1)v1与v2大小什么关系?
(2)试推导r1v1=v2r2
【考向洞察】
近似计算可以使题目更加简单!
【知识提升】
①行星运动 近似圆 处理。
②开普勒行星运动定律不仅适用于行星绕太阳运转,对于卫星绕行星运转,也遵循类似的运动规律。
③比例系数k与 有关,与行星或卫星质量无关,是个常量,但不是恒量,在不同的星系中,k值 。
万有引力定律
【知识固本】
万有引力定律的内容:
自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与 成正比、与它们之间 成反比。即F= ,G为引力常量,通常取G=6.67×10-11N·m2/kg2,由物理学家卡文迪什测定。
【典型例题】1、有一质量为M、半径为R、密度均匀的球体,在距离球心O为2R的地方有一质量为m的质点。现从球体中挖去半径为0.5R的小球体,如图所示,引力常量为G,则剩余部分对m的万有引力为( )
A. B. C. D.
“挖补法”求解万有引力
【知识提升】
万有引力定律的适用条件
①公式适用于 间的相互作用,当两个物体间的距离远大于物体本身的大小时,物体可视为质点。
②质量分布均匀的球体可视为质点,r是两 间的距离。
【典型例题】2、(2024·广东广州高三期中)2020年9月,我国明确提出2030年“碳达峰”与2060年“碳中和”目标。人类社会的快速进步使得碳排放量不断增加,这导致温室效应加剧,地球南北两极的生态环境遭到一定的破坏。一头质量为m的北极熊在失去家园后,被运送到了位于赤道上的北极熊馆加以照料,它在北极和馆内的重力差为ΔF。已知地球自转周期为T。根据以上信息,可求出地球的半径为( )
A. B. C. D.
【知识提升】
自转模型
(1)万有引力与重力的关系
地球对物体的万有引力F表现为两个效果:一是重力mg,二是提供物体随地球自转的向心力F向,如图所示。
①在赤道上:G=
②在两极上:G=
③在一般位置:万有引力G等于重力mg与向心力F向的矢量和。
越靠近南北两极g值 ,由于物体随地球自转所需的向心力较小,常认为万有引力近似等于重力。
(2)重力的方向:①赤道与两极指向 ;②其它位置与水平面垂直或竖直向下,但不指向 。
【深入思考】
两极和赤道上的重力加速度如何表示?天上和地下呢?
地下 地面 天上
两极或不计自转 赤道
g= g= g= -Rω自2 g=
【典型例题】3、近几年来,我国生产的“蛟龙号”下潜突破7 000 m大关,我国的北斗导航系统也进入紧密的组网阶段。已知质量分布均匀的球壳对壳内任一质点的万有引力为零,将地球看成半径为R、质量分布均匀的球体,北斗导航系统中的一颗卫星的轨道距离地面的高度为h,“蛟龙号”下潜的深度为d,则该卫星所在处的重力加速度与“蛟龙号”所在处的重力加速度的大小之比为( )
A. B. C. D.
【知识提升】
球体内部万有引力的两个有用推论
(1)推论1:在匀质球壳的空腔内任意位置处,质点受到球壳的万有引力的合力为零,即ΣF引=0.
(2)推论2:在匀质球体内部距离球心r处的质点(m)受到的万有引力等于球体内半径为r的同心球体(M′)对其的万有引力,即F=G。
【考向洞察】
天体质量和密度的计算
【知识固本】
计算中心天体的质量和密度
“一个中心、两个基本点”——需要已知量r、T(或ω、v);g、R
原理 “天上”环绕法 “地上”黄金代换法
万有引力提供向心力: == 万有引力等于重力:
质量 M= = = M=
密度 ρ= = = ρ=
【典型例题】4、我国是第三个对火星探测并将探测器着陆火星的国家,探测器在环绕火星表面飞行时周期是T。火星表面气体非常稀薄可近似认为真空,在火星表面附近以初速度v0水平抛出一个物体,测得抛出点距火星表面高度为h,落到火星表面时物体的水平位移为x,已知引力常量为G,下列说法正确的是( )
A.火星表面重力加速度大小是 B.火星的半径是
C.火星的质量是 D.火星的密度是
【知识提升】
1.只能计算出中心天体的质量和密度。
2.若卫星绕天体表面运行,可认为轨道半径r等于天体半径R,则天体密度ρ=
【考向洞察】
【课堂小结】
利用3-5分钟时间,对本节课学习的内容进行总结梳理
【达标检测】
1.(2024·江苏南京模拟)某行星绕太阳运动的轨道如图所示,则以下说法正确的是( )
A.该行星在a点的向心加速度比在b、c两点的都大
B.该行星在a点的速度比在b、c两点的速度都更小
C.行星与太阳的连线在相等时间内扫过的面积是不相等的
D.行星绕太阳做匀速圆周运动,太阳在圆心上
2.某类地天体可视为质量分布均匀的球体,由于自转的原因,其表面“赤道”处的重力加速度为g1,“极点”处的重力加速度为g2,若已知自转周期为T,则该天体的半径为( )
A. B. C. D.
3.2022年8月10日,我国在太原卫星发射中心用长征六号运载火箭成功将“吉林一号”组网星中的16颗卫星发射升空,卫星顺利进入预定的环绕地球运动轨道,发射任务取得圆满成功。这16颗卫星的轨道平面各异,高度不同,通过测量发现,它们的轨道半径的三次方与运动周期的二次方成正比,且比例系数为p。已知引力常量为G,由此可知地球的质量为( )
A. B. C. D.
4. 某行星周围的卫星绕其做圆周运动的轨道半径r与运行周期T的关系如图4所示。行星的半径为R0,引力常量为G,图中a、b为已知量。下列说法正确的是( )
A.绕该行星表面运行卫星的周期为 B.该行星的质量为
C.该行星的密度为 D.该行星表面的重力加速度为
同课章节目录
