中考复习基础知识：一次函数

年 月 日 第 周 星期 第 节
课 题 一次函数 课 型 复习课
教学目标 知识目标:经历一次函数等概念的抽象概括过 ( http: / / www.21cnjy.com )程，体会函数及变量思想，进一步发展抽象思维能力；经历一次函数的图象及其性质的探索过程，在合作与交流活动中发展合作意识和能力．
能力目标:经历函数图象信息的识别与应用过程 ( http: / / www.21cnjy.com )，发展形象思维能力．初步理解一次函数的概念；理解一次函数及其图象的有关性质；初步体会方程和函数的关系．能根据所给信息确定一次函数表达式；会作一次函数的图象
情感目标:经历利用一次函数及其图象解决实际问题的过程，发展数学应用能力
教学重点 一次函数的概念、图像及其性质
教学难点 运用一次函数的图象及其性质解决有关实际问题
教学方法 讲练结合 教 具
课堂考勤记录
教 学 程 序
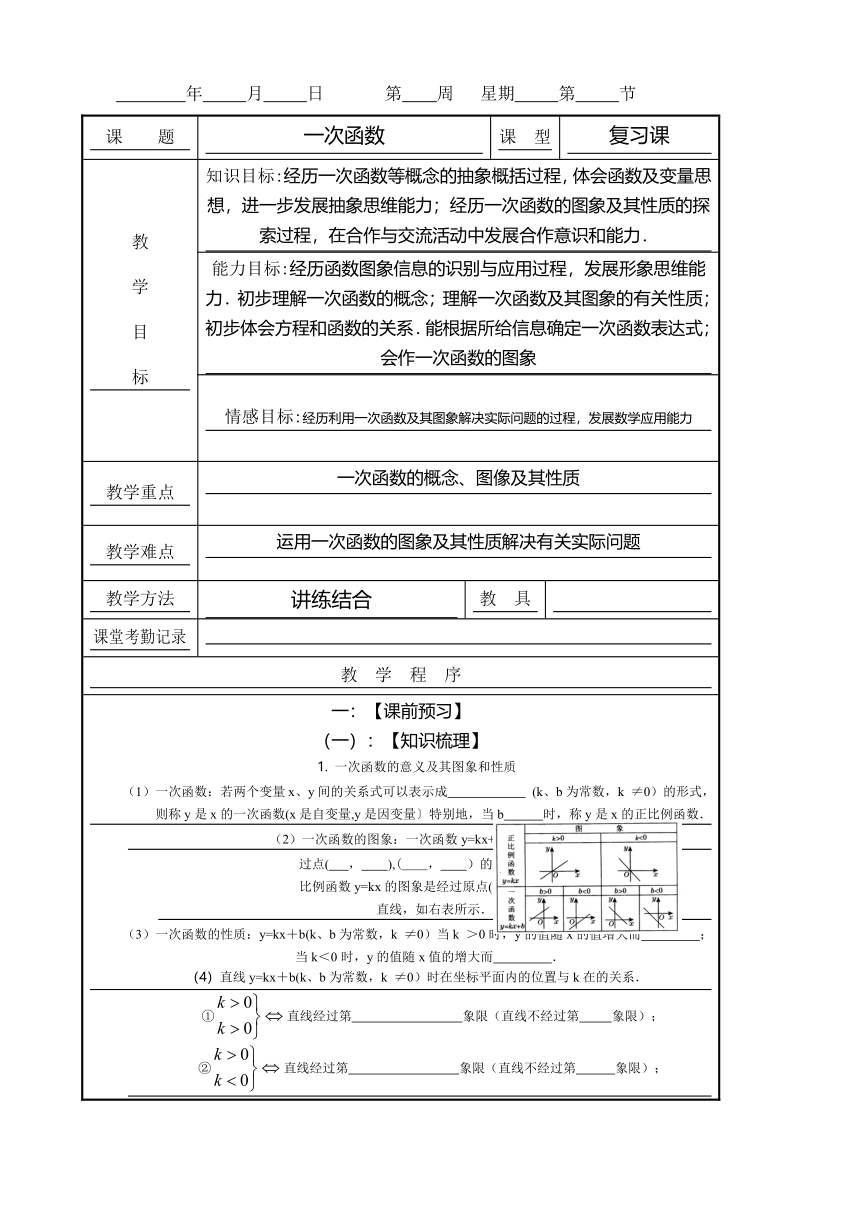
一：【课前预习】（一）：【知识梳理】 1. 一次函数的意义及其图象和性质 （1）一次函数：若两个变量x、y ( http: / / www.21cnjy.com )间的关系式可以表示成 (k、b为常数，k ≠0）的形式，则称y是x的一次函数(x是自变量,y是因变量〕特别地，当b 时，称y是x的正比例函数．（2）一次函数的图象：一次函数y=kx+b的图象是经过点( ， ),( ， ）的一条直线，正比例函数y=kx的图象是经过原点(0，0）的一条直线，如右表所示． （3）一次函数的 ( http: / / www.21cnjy.com )性质：y=kx＋b(k、b为常数，k ≠0）当k ＞0时，y的值随x的值增大而 ；当k＜0时，y的值随x值的增大而 ． （4）直线y=kx＋b(k、b为常数，k ≠0）时在坐标平面内的位置与k在的关系．①直线经过第 象限（直线不经过第 象限）；②直线经过第 象限（直线不经过第 象限）；③直线经过第 象限（直线不经过第 象限）；④直线经过第 象限（直线不经过第 象限）； 2. 一次函数表达式的求法 （1）待定系数法：先设出解析 ( http: / / www.21cnjy.com )式，再根据条件列方程或方程组求出未知系数，从而写出这个解析式的方法，叫做待定系数法，其中的未知系数也称为待定系数。 （2）用待定系数法求出函 ( http: / / www.21cnjy.com )数解析式的一般步骤：① ；② 得到关于待定系数的方程或方程组；③ 从而写出函数的表达式。 （3）一次函数表达式的求 ( http: / / www.21cnjy.com )法：确定一次函数表达式常用待定系数法，其中确定正比例函数表达式，只需一对x与y的值，确定一次函数表达式，需要两对x与y的值。二：【经典考题剖析】 1.在函数y=－2x+3中当自变量x满足______时，图象在第一象限．解：0＜x＜ 点拨：由y=2x+3可知图象过一、二、四象限，与x轴交于(，0)，所以，当0＜x＜时，图象在第一象限．2.已知一次函数y=(3a+2)x－(4－b),求字母a、b为何值时：（1）y随x的增大而增大；（2）图象不经过第一象限；（3）图象经过原点；（4）图象平行于直线y=－4x+3；（5）图象与y轴交点在x轴下方．3.杨嫂在再就业中心的扶持下，创办了“润杨” ( http: / / www.21cnjy.com )报刊零售点，对经营的某种晚报，杨嫂提供了如下信息：（1）买进每份0．2元，卖出每份0．3元；（2）一个月内（以30天计）有20天每天可以卖出200份，其余10天每天只能卖出120份；（3）一个月内，每天从报社买进的报纸数必须相同,当天卖不掉的报纸，以每份0．1元退给报社． ①填下表：②设每天从报社买进该种晚报x份(120≤x≤200 )时，月利润为y元，试求出y与x之间的函数表达式，并求月利润的最大值．4.某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用后，那么服药后2小时血液中含药量最高，达每毫升6微克，（1微克＝10－3毫克），接着逐步衰减，10小时时血液中含量为每毫升3微克，每毫升血液中含药量（微克）随时间（小时）的变化如图所示。当成人按规定剂量服用后：（1）分别求出≤2和≥2时与之间的函数关系式；（2）如果每毫升血液中含药量为4微克或4微克以上时，在治疗疾病时是有效的，那么这个有效的时间是多长？解析：（1）设≤2时，，把坐标（2，6）代入得：；设≥2时，，把坐标（2，6），（10，3）代入得：。（2）把代入与中得：，，则（小时），因此这个有效时间为6小时。5. 如图，直线 相交于点A， 与x轴的交点坐标为（－1，0）， 与y轴的交点坐标为（0，－2），结合图象解答下列问题：⑴求出直线 表示的一次函数的表达式；⑵当x为何值时， 表示的两个一次函数的函数值都大于0？三：【课堂小结】
作业或练习
课后反思