数学六年级下人教版3.1圆柱的表面积课件
文档属性
| 名称 | 数学六年级下人教版3.1圆柱的表面积课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-07 20:07:45 | ||
图片预览









文档简介
(共79张PPT)
准备活动
侧面积
表面积
基本练习
提高练习
拓展练习
复习:
准备活动:
1、圆的周长公式:
2、圆的面积公式:
C=2∏R或C=∏D
S=π( )2
S=π(d÷2)2
S=π(C÷π÷2)2
S=πr2
或
知道半径:
知道直径:
知道周长:
复习:
准备活动:
周长:3.14×4=
3、计算:在圆中,
(1)、已知d=4厘米,求C=?S=?
12.56(厘米)
面积:3.14×
3.14×4
=12.56(平方厘米)
周长:2×3.14×4=
(2)、已知r =4分米,求C=?S=?
面积:3.14×
3.14×16
=50.24(平方分米)
25.12(分米)
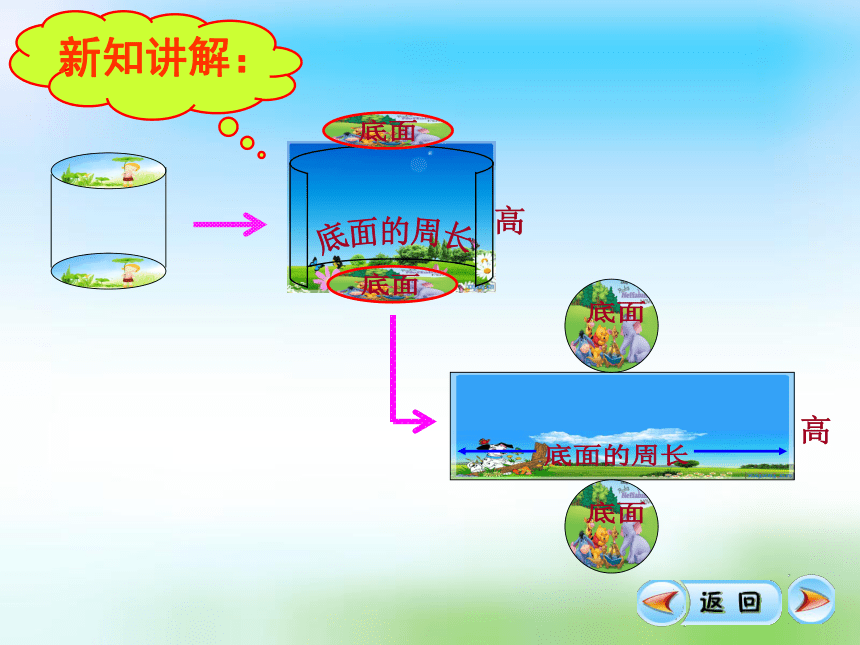
新知讲解:
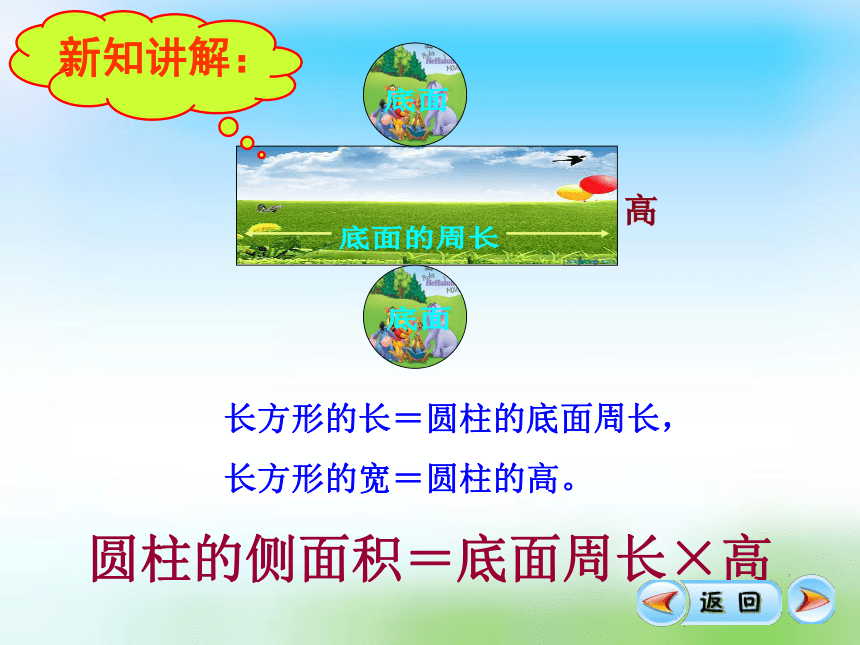
圆柱的侧面积=底面周长×高
长方形的长=圆柱的底面周长,
长方形的宽=圆柱的高。
新知讲解:
4、圆柱体的各部分名称和特征是什么?
圆柱体侧面积计算公式的推导:
圆柱体的侧面展开是一个长方形,这个长方形的长等于圆柱底面的周长,宽等于圆柱的高,
因为 长方形的面积=长×宽 ,
所以 圆柱体的侧面积=底面周长×高
新知讲解:
1 一个圆柱,底面的直径是0.5米,高是1.8米,求它的侧面积。
3.14×0.5×1.8
= 3.14×0.9
≈ 2.83
(平方米)
答:它的侧面积是2.83平方米。
新知讲解:
计算下面圆柱的侧面积
(1)底面周长4.2厘米,高2厘米.
(2)底面直径3厘米,高4厘米.
(3)底面半径1厘米,高3.5厘米.
4.2 ×2=8.4(平方厘米)
3.14 ×3 ×4=37.68(平方厘米)
2 ×3.14 ×1 ×3.5=21.98(平方厘米)
尝试练习:
1、圆柱有( )个底面,它们是( );有( )侧面,是( ),有( )条高,这些高都( )。
2、圆柱的侧面展开是( ),长方形的长等于( ),宽等于( )。
3、圆柱的侧面积=
2
大小一样的圆
1
曲面
无数
长度相等
长方形
底面周长
高
底面周长×高
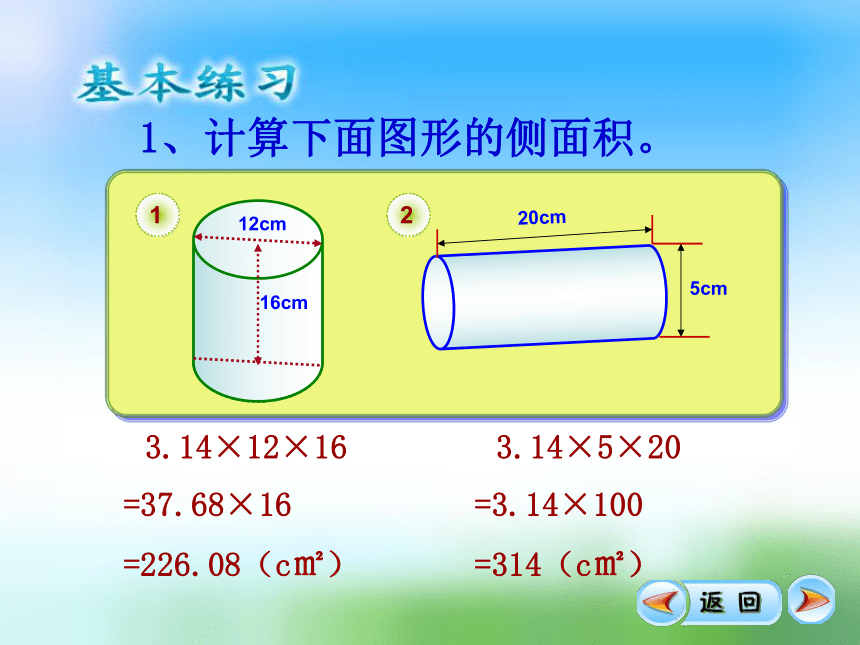
尝试练习:
1、计算下面图形的侧面积。
12cm
16cm
5cm
20cm
1
2
3.14×12×16
=37.68×16
=226.08(c㎡)
3.14×5×20
=3.14×100
=314(c㎡)
2、(如图)如果给下面的笔筒的侧面贴上彩纸,至少需要用多少彩纸?
13cm
8cm
3.14×8×13
=25.12×13
=326.56(c㎡)
答:至少需要326.56平方厘米。
1、求下列圆柱体的侧面积
(1)底面半径是3厘米,高是4厘米;
(2)底面直径是4厘米,高是5厘米。
(3)底面周长是12.56厘米,高是4厘米。
4×(3×2×3.14)=75.36(cm2)
5×(4×3.14)=62.8(cm2)
4×12.56=50.24(cm2)
尝试练习:
给柱子上涂漆,求涂漆部分面积。
压路机滚筒压过的路面的面积
1、一台压路机的前轮是圆柱形,轮宽2m,直径1.2m.前轮转动一周,压路的面积是多少㎡?
3.14×1.2×2
=3.768×2
=7.536(㎡)
答:至少需要7.536 ㎡。
一台压路机的前轮是圆柱形,轮宽2米,滚筒直径是轮宽的60%,每分钟转动20周,每分钟压路的面积是多少平方米?
3.14×1.2×2×20
底面周长
圆柱侧面积
2×60%=1.2(米)
尝试练习:
一个压路机的前轮是圆柱,轮宽
1.5米,直径1.2米,前轮转动一周,
压路的面积是多少平方米
尝试练习:
①用一张长8cm、宽5 cm的长方形纸围成一个圆柱体,这个圆柱体的侧面积是( )cm2。
②一根10米长的圆柱形排水钢管,量得横截面圆的半径是0.2米,如果在钢管的表面喷上防锈油漆,喷漆面积是( )平方米。
40
4π
尝试练习:
1、什么叫物体的表面积?
围成立体图形所有面的总面积叫做这个物体的表面积。
2、你会计算下面哪些图形的表面积?
1、正方体有什么特征?
2、你会计算下面正方体的表面积吗?写出正方体表面积计算公式。
正方体有6个面,都是正方形。6个面的面积都相等;有12条棱,它们的长度也都相等;有8个顶点。
正方体的表面积=棱长×棱长×6
1、长方体有什么特征?
2、你会计算下面长方体的表面积吗?写出长方体表面积计算公式。
长方体有6个面,都是长方形(注意:在特殊的长方体中有一组对面是正方形)。对面面积都相等;有12条棱可分长、宽、高三组,每组4条长度相等;有8个顶点。
长方体的表面积=(长×宽+长×高+宽×高)×2
说一说,圆柱是由哪几部分组成的?圆柱各部分都有什么特征?
圆柱是由两个圆面和周围的一个曲面组成的。
圆柱的两个圆面叫做底面。它们是两个完全一样的圆。
形状相同,大小相等
周围的(这一个)曲面叫做侧面。
两个底面之间的距离叫做圆柱的高
圆柱的侧面沿高剪下,展开后是一个长方形。议一议,这个长方形的长、宽与圆柱的什么有关?有什么关系?为什么?
长
宽
这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
1、圆柱的表面积指的是什么?
2、圆柱的表面积怎样计算?为什么?
围成圆柱所有面的总面积叫做圆柱的表面积。
长
宽
圆柱的表面积=
侧面积+底面积
×2
因为圆柱的侧面沿高剪下,展开后是一个长方形。这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
所以:
长方形的面积
圆柱的侧面积
= 长 × 宽
底面周长
高
= ×
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
S表面积=2πr×h + 2×πr2
深入认识:
圆柱的表面由上、下两个底面和一个侧面组成的立体图形。
1 一个圆柱的高是15厘米,底面半径是5厘米,它的表面积是多少?
(1)侧面积:
2×3.14×5×15=471(平方厘米)
(2)底面积:3.14× =78.5(平方厘米)
(3)表面积:471+78.5×2=628(平方厘米)
答:它的表面积是628平方厘米。
新知讲解:
2、 一个圆柱,底面直径是5厘米,高是4厘米,求它的表面积是多少
答:它的表面积是102.05平方厘米.
(1)侧面积:
(2)底面积:
(3)表面积:
3.14×5×4 = 62.8(平方厘米)
3.14×( ) = 19.625(平方厘米)
62.8+ 19.625 ×2 =102.05 (平方厘米)
圆柱的表面积=侧面积+底面面积×2
新知讲解:
3. 一个圆柱,底面周长是94.2厘米,高是25厘米,求它的侧面积。
5. 砌一个圆柱形沼气池,底面直径是4米,深是2米。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?
94.2×25=235.5(平方厘米)
4. 一个圆柱,底面直径是2分米,高是45分米,求它的表面积。
3.14×2×45+3.14×12×2
=282.6+6.28
=288.88(平方分米)
3.14×4×2+3.14×22
=25.12+12.56
=37.68(平方米)
答:抹水泥的面积是37.68平方米。
6.求下列圆柱体的表面积
(1)底面半径是4米,高是6米;
(2)底面直径是6分米,高是12分米。
(3)底面周长是25.12厘米,高是8厘米。
表:50.24×2+150.72=251.2(m2)
侧:6×(4×2×3.14)=150.72(m2)
底:42×3.14=50.24(m2)
表:28.26×2+226.08= 282.6 (m2)
侧:12×(6×3.14)=226.08(m2)
底:(6÷2)2×3.14=28.26(m2)
表:50.24×2+200.96= 301.44(m2)
侧:8×25.12=200.96(m2)
底:(25.12÷3.14÷2)2×3.14=50.24(m2)
新知讲解:
1、一顶圆柱形厨师帽,高28㎝,冒顶直径是20 ㎝,做一顶帽子需要多少面料?(得数保留整十平方厘米)
(1)、帽子的侧面积:
3.14×20×28=1758.4(平方厘米)
(2)、帽顶的面积:
3.14×(20÷2)=314(平方厘米)
(3)、需要用的面料:
1758.4+ 314 =2072.4(平方厘米)
≈2070(平方厘米)
答:需要用2070平方厘米的面料。
(1)、帽子的侧面积:
3.14×20×28=1758.4(平方厘米)
(2)、帽顶的面积:
3.14×(20÷2)=314(平方厘米)
(3)、需要用的面料:
1758.4+ 314 =2072.4(平方厘米)
≈2080(平方厘米)
答:需要用2080平方厘米的面料。
注意:今后在计算原材料得数要求取近似数时,为了保证材料的够用,不能用四舍五入法,而必须用进一法。
2. 一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米? (得数保留整百)
(1)侧面积:
3.14×20×24=1507.2(平方厘米)
(2)底面积:3.14× =314(平方厘米)
(3)表面积:1507.2+314=1821.2
答:做这个水桶要用铁皮约1900平方厘米。
≈1900(平方厘米)
新知讲解:
3、 一个没有盖的圆柱形纸盒,底面直径是5厘米,高是4厘米,做这个纸盒要用纸皮多少平方厘米?(得数保留整十平方厘米)
(3)需要纸皮:
≈90(平方厘米)
(1)纸盒侧面积:
(2)纸盒底面积:
答:做这个纸盒要用纸皮 90平方厘米
约
3.14×5×4 =62.8(平方厘米)
3.14×( ) = 19.625(平方厘米)
62.8+ 19.625 = 82.425
尝试练习:
4.一个没有盖的圆柱形铁皮水桶,高是24分米,底面直径是高的 ,做这个水桶要用铁皮多少平方分米?(得数保留整百平方分米)
(1) 底 面 直 径: 24× =20(分米)
(2)水桶的侧面积: 3.14×20×24 =1507.2(平方分米)
(4)需要铁皮: 1507.2+ 314 = 1821.2≈1900(平方分米)
答:做这个水桶用铁皮约1900平方分米。
(3)水桶的底面积: 3.14×( ) =314(平方分米)
尝试练习:
(1)侧面积:2 ×3.14 ×2 ×4.5=56.52 (c㎡)
(2)底面积:3.14 ×22 =12.56 (c㎡)
(3)表面积:56.52+12.56 × 2=81.64 (c㎡)
尝试练习:
1、计算下面图形的表面积。
12cm
16cm
5cm
20cm
1
2
3.14×12×16=226.08(c㎡)
3.14×5×20 =314(c㎡)
我叫
圆柱
我的高
是 4 厘米
我的底面周长
是 12.56 厘米
你们能帮我算出表面积吗?
帮一帮
尝试练习:
现在有一个罐头厂计划用铁皮制作一批底面半径5厘米,高10厘米的圆柱形罐头盒。你能不能帮厂长算一算制作一个至少需要多少平方厘米铁皮?
应用与实践
6.28
2
2
4
4
3
3
2
4
3
轻松一刻
A
B
C
下面哪个图形是圆柱的展开图?
15
3
请帮下面的长方形找底面,使它们能组成圆柱.(单位:厘米)
9.42
r=1.5
( )
r=3
( )
×
√
1、做一个圆柱形的汽油桶,底面直径0.6米,高1米,做这样一个汽油桶大约需要多少平方米的铁皮
2、做一个圆柱形通风管,长2米,管口半径5厘米,做这样一个通风管至少需要多少平方米铁皮
3、一个圆柱形的汽油桶,从里面量,底面直径是40厘米,高1.2米。做这个油桶至少需要多少铁皮?
4、有一根长3.5米的圆柱子,它的底面周长是12.56米。如果给这个圆柱的侧面刷一层漆。刷漆的面积是多少平方米?
5、一节圆柱形烟筒,底面直径是8厘米,长1.5米,做1000节这样的烟筒至少需要用白铁皮多少平方米?
6、一个圆柱,底面周长是94.2厘米,高是25厘米,求它的侧面积。
7、学校食堂要用铁皮做一根横截面半径是3分米,高是3米的圆柱形烟囱,至少需要多少平方米的铁皮?
8、修建一个圆柱形沼气池,底面直径是4米,深是2米。在池的四壁与底面抹上水泥,抹水泥部分的面积是多少平方米?
9、小明做了一个笔筒,他想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸
10.制作一个底面直径20厘米、长50厘米的圆柱形通风管,至少要用多少平方厘米的铁皮?
判断:(对的打“√”,错的打“×”
(1)圆柱体只有一条高。 ( )
(2)圆柱体的侧面积总比表面积小。 ( )
(3)制作一个铁皮烟囱,所用的铁皮面积求圆柱就是侧面积。 ( )
(4)圆柱的侧面是一个平行四边形。 ( )
(5)如果一个圆柱体的侧面展开后是一个正方形,那么圆柱的高是底面半径的2Π倍.( )
√
×
×
√
×
做一个无盖锅所需铁皮面积
说一说该求哪部分的面积
做茶叶桶所需铁皮面积
商标纸面积
求下列圆柱形物体用料的面积,应计算哪些面的总面积?
铁片制成的糖果盒
玻璃杯
铁皮油桶
侧面+2个底面
侧 面
侧面+1个底面
侧 面
侧面+2个底面
塑料制成的水管
水泥烟囱
我来解决生活中的问题
(1)把一个圆柱体侧面展开, 可能得到一个长方形, 这个长方形的长等于圆柱的( ), 宽等于圆柱的( )。
(2)压路机滚动一周能压多少路面是求( )的面积。
(3)做一个无盖的圆柱形水桶,所用铁皮多少,用( )面积加上( )个底面面积。
(4)一支(圆柱形)铅笔,求它需要涂漆的部分,是计算它的( )面积,用底面的( )乘以( )。
圆柱侧面
侧面
一个
侧面
周长
高
口答下列各题
底面周长
高
1.冬天护林工人给圆柱形的树干的下端涂防蛀涂料,那么粉刷树干的面积是指( ).
A.底面积 B.侧面积
C.表面积 D.体积
B
小结:
在解答实际问题前一定要
先进行分析,看它们求的
是哪部分面积,再选择解
答的方法。
1、一个没有盖的圆柱形铁皮水桶,高是48厘米,底面直径是30厘米,做这个水桶至少要用铁皮多少平方厘米?(得数保留整百平方厘米)。
(1)水桶的侧面积:
3.14 ×30 ×48=4521.6(平方厘米)
(2)水桶的底面积:
3.14 ×(30/2) 2 =3.14 ×15 2 =3.14 ×225=706.5(平方厘米)
(3)需要铁皮:
4521.6+706.5=5228.1≈5300(平方厘米)
2.砌一个圆柱形的沼气池,底面直径是3米,
深是2米,在池的周围与底面抹上水泥,
抹上水泥的部分面积是多少平方米?
思考题
1. 一个圆柱体的侧面展开是个边长9.42厘米的正方形,这个圆柱体的表面积是多少平方厘米?(得数保留两位小数)
9.42×9.42+3.14×(9.42÷3.14)2×2
=88.728+14.13
≈102.86(平方厘米)
答:这个圆柱体的表面积是102.86平方厘米。
2. 一个圆柱体的侧面积是226.08平方厘米,底面半径4厘米,它的高是多少?
226.08÷(2×3.14×4)
=226.08÷25.12
=9(厘米)
答:它的高是9厘米。
3. 把一段长20分米的圆柱形木头沿着底面直径劈开,表面积增加80平方分米,原来这段圆柱形木头的表面积是多少?
4.砌一个圆柱形水池,底面周长是25.12米,深2米,要在它的底面和四周抹上水泥,如果每平方米用水泥10千克,共需水泥多少千克?
80÷2=40(平方分米)(一个长方形面积)
40÷20=2(分米)(底面直径)
2×3.14×20=125.6(平方分米) (侧面积)
3.14×(2÷2) ×2=6.28(平方分米)(底面积和)125.6+6.28=131.88(平方分米)(表面积)
答:原来这段圆柱形木头的表面积是131.88平方分米。
(1)求底面面积:3.14×4×4=50.24(平方米)
(2)侧面积:25.12×2=50.24(平方米)
(3)总面积: 50.24+50.24=100.48(平方米)
(4)共需水泥:100.48×10=100.48 (千克)
答:共需水泥1004.8千克。
圆的半径:25.12÷3.14÷2=4(米)
1、把一个底面直径是16分米,高15分米的圆柱,分成四个小圆柱,表面积比原来增加了多少平方分米?
2、一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)
3、将一个圆柱的侧面展开,得到一个边长是15、7厘米的正方形。求原来圆柱的侧面积。
4、做50节同样大小的圆柱形通风管,每节长4米,管口直径是10厘米,至少需要多少平方米的铁皮?
5、压路机的滚筒是一个圆柱形,它的宽是1、5米,滚筒横截面的半径是0、6米,以每分钟滚动5周计算,每分钟压路的面积是多少平方米?
1、圆柱的高是15.7厘米,侧面展开是个正方形,圆柱的侧面积是多少平方厘米?
2、圆柱的高是15.7厘米,侧面展开是个正方形,圆柱的表面积是多少平方厘米?
3、大厅里有8根圆柱形柱子,每根的底面直径4分米,高3米,如果每平方米需油漆费0.5元,漆这8根柱子约需要油漆费多少元?
4、把一个底面半径是7分米,高15分米的圆柱沿着垂直于底面分为两个半圆柱,表面积增加了多少平方分米?
5、一个圆柱的侧面积是188.4平方分米,底面半径是2分米,它的高是多少分米
我来做裁判.
1、求下面各圆柱的表面积。
(1)底面直径是12厘米,高是16厘米。
3.14×12×16+3.14×( ) ×2 ( )
(2)底面半径是5分米,高是20分米。
2×3 .14× 5×20+ 3 .14× 5 ( )
√
×
2、圆柱的侧面展开后一定是长方形. ( )
3、做一个无盖的圆柱水桶,需要的铁皮的
面积是圆柱的表面积。 ( )
4、一个圆柱的底面半径扩大4倍,高不变,
它的侧面积就扩大16倍.( )
√
×
×
20π厘米
15π厘米
它们的表面积相等吗
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
分两种情况:
1、以20π厘米为底面周长,10 π厘米为高。
2、以10 π厘米为底面周长 ,20 π厘米为高。
10 π
20π
20 π
10π
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以20π厘米为底面周长,10 π厘米为高。
解:C=20 π厘米,
h=10 π厘米
S侧=Ch
=20 π×10 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=10(cm)
S底= πr2=100 π(cm2)
S表=S侧+2S底=(200 π2+200 π )cm2
20π
10π
答:这个圆柱的表面积为(200π2+200π)cm2或(200π2+50π)cm2
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以10π厘米为底面周长,20 π厘米为高。
解:C=10 π厘米,
h=20 π厘米
S侧=Ch
=10 π×20 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=5(cm)
S底= πr2=25 π(cm2)
S表=S侧+2S底=(200 π2+50 π )cm2
10π
20π
动脑筋
10
S侧=3.14 × 6 × 10=188.4(cm2)
下面两个圆柱体的侧面积、表面积是否相等?(单位:厘米)
10
6
6
S底=3.14 × (6/2)2=28.26(cm2)
S表=S侧+2S底=244.92(cm2)
S侧=3.14 × 10 × 6=188.4(cm2)
S底=3.14 × (10/2)2=78.5(cm2)
S表=S侧+2S底=345.4(cm2)
两个圆柱的侧面积相等,表面积不相等。
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
3、一根圆柱形木料长20dm,把它截成4个相等的小段, 表面积增加了18.84d㎡。横截面的面积是 ( )
3.14d㎡
4、一根长2米、底面直径是4厘米的圆柱形木料,把它锯成同样长的4段,表面积比原来增加了( )平方厘米。
动脑筋
5、如图:把一个底面是6cm2,高4cm的圆柱沿着高切开,分成3个小圆柱,它的表面积增加( )cm2.
A、12
B、18
C、24
D、36
C
1、把一个底面直径为5厘米,高是8厘米的圆柱体沿底面直径切开,分成形状大小完全相同的两部分,它们的表面积比原来增加多少平方厘米?
动脑筋
有一根圆柱形的木材,底面直径是16厘米,高是20厘米沿着它的底面直径, 从上向下锯成相等的两块(如图),每块的表面积是多少
动脑筋
2、李师傅把一根高1米的圆柱形木料,沿底面直径平均分成两部分,这时表面积比原来增加了0.8平方米。求这根木料原来的表面积。
(1)底面直径: 0.8 ÷2 ÷1=0.4 (m)
(2)圆柱的表面积:
3.14×(0.4÷2)×2+3.14×0.4×1
=0.2512+1.256
=1.5072(平方米)
答:这根木料原来的表面积是1.5072平方米。
挑战自我
把一个高10厘米的圆柱,按下图切开,拼成一个近似的长方体。表面积就增加了( )平方厘米.
60
挑战自我
1、一个圆柱体的侧面积是72π cm2,底面半径4 cm,它的高是多少?
解:72π÷(2×π×4)
=72π÷8π
=9(cm)
答:它的高是9 cm。
2、一个圆柱体的侧面展开是个边长9.42 cm的 正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
解:9.42×9.42+3.14(9.42÷3.14÷2)2×2
=88.728+14.13
≈102.86( cm2 )
答:这个圆柱体的表面积是102.86 cm2。
挑战自我
挑战自我
用一个棱长是6分米的正方体,削成一个最大的圆柱体,这个圆柱的表面积是多少?
左图是一个圆柱形状的蛋糕盒,底面半径15厘米,高20厘米。
(1)做这个蛋糕盒大约需要用多少平方厘米的纸板?
(2)像左图那样用彩带包扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用15厘米彩带)
运用知识解决问题
全课总结
准备活动
侧面积
表面积
基本练习
提高练习
拓展练习
复习:
准备活动:
1、圆的周长公式:
2、圆的面积公式:
C=2∏R或C=∏D
S=π( )2
S=π(d÷2)2
S=π(C÷π÷2)2
S=πr2
或
知道半径:
知道直径:
知道周长:
复习:
准备活动:
周长:3.14×4=
3、计算:在圆中,
(1)、已知d=4厘米,求C=?S=?
12.56(厘米)
面积:3.14×
3.14×4
=12.56(平方厘米)
周长:2×3.14×4=
(2)、已知r =4分米,求C=?S=?
面积:3.14×
3.14×16
=50.24(平方分米)
25.12(分米)
新知讲解:
圆柱的侧面积=底面周长×高
长方形的长=圆柱的底面周长,
长方形的宽=圆柱的高。
新知讲解:
4、圆柱体的各部分名称和特征是什么?
圆柱体侧面积计算公式的推导:
圆柱体的侧面展开是一个长方形,这个长方形的长等于圆柱底面的周长,宽等于圆柱的高,
因为 长方形的面积=长×宽 ,
所以 圆柱体的侧面积=底面周长×高
新知讲解:
1 一个圆柱,底面的直径是0.5米,高是1.8米,求它的侧面积。
3.14×0.5×1.8
= 3.14×0.9
≈ 2.83
(平方米)
答:它的侧面积是2.83平方米。
新知讲解:
计算下面圆柱的侧面积
(1)底面周长4.2厘米,高2厘米.
(2)底面直径3厘米,高4厘米.
(3)底面半径1厘米,高3.5厘米.
4.2 ×2=8.4(平方厘米)
3.14 ×3 ×4=37.68(平方厘米)
2 ×3.14 ×1 ×3.5=21.98(平方厘米)
尝试练习:
1、圆柱有( )个底面,它们是( );有( )侧面,是( ),有( )条高,这些高都( )。
2、圆柱的侧面展开是( ),长方形的长等于( ),宽等于( )。
3、圆柱的侧面积=
2
大小一样的圆
1
曲面
无数
长度相等
长方形
底面周长
高
底面周长×高
尝试练习:
1、计算下面图形的侧面积。
12cm
16cm
5cm
20cm
1
2
3.14×12×16
=37.68×16
=226.08(c㎡)
3.14×5×20
=3.14×100
=314(c㎡)
2、(如图)如果给下面的笔筒的侧面贴上彩纸,至少需要用多少彩纸?
13cm
8cm
3.14×8×13
=25.12×13
=326.56(c㎡)
答:至少需要326.56平方厘米。
1、求下列圆柱体的侧面积
(1)底面半径是3厘米,高是4厘米;
(2)底面直径是4厘米,高是5厘米。
(3)底面周长是12.56厘米,高是4厘米。
4×(3×2×3.14)=75.36(cm2)
5×(4×3.14)=62.8(cm2)
4×12.56=50.24(cm2)
尝试练习:
给柱子上涂漆,求涂漆部分面积。
压路机滚筒压过的路面的面积
1、一台压路机的前轮是圆柱形,轮宽2m,直径1.2m.前轮转动一周,压路的面积是多少㎡?
3.14×1.2×2
=3.768×2
=7.536(㎡)
答:至少需要7.536 ㎡。
一台压路机的前轮是圆柱形,轮宽2米,滚筒直径是轮宽的60%,每分钟转动20周,每分钟压路的面积是多少平方米?
3.14×1.2×2×20
底面周长
圆柱侧面积
2×60%=1.2(米)
尝试练习:
一个压路机的前轮是圆柱,轮宽
1.5米,直径1.2米,前轮转动一周,
压路的面积是多少平方米
尝试练习:
①用一张长8cm、宽5 cm的长方形纸围成一个圆柱体,这个圆柱体的侧面积是( )cm2。
②一根10米长的圆柱形排水钢管,量得横截面圆的半径是0.2米,如果在钢管的表面喷上防锈油漆,喷漆面积是( )平方米。
40
4π
尝试练习:
1、什么叫物体的表面积?
围成立体图形所有面的总面积叫做这个物体的表面积。
2、你会计算下面哪些图形的表面积?
1、正方体有什么特征?
2、你会计算下面正方体的表面积吗?写出正方体表面积计算公式。
正方体有6个面,都是正方形。6个面的面积都相等;有12条棱,它们的长度也都相等;有8个顶点。
正方体的表面积=棱长×棱长×6
1、长方体有什么特征?
2、你会计算下面长方体的表面积吗?写出长方体表面积计算公式。
长方体有6个面,都是长方形(注意:在特殊的长方体中有一组对面是正方形)。对面面积都相等;有12条棱可分长、宽、高三组,每组4条长度相等;有8个顶点。
长方体的表面积=(长×宽+长×高+宽×高)×2
说一说,圆柱是由哪几部分组成的?圆柱各部分都有什么特征?
圆柱是由两个圆面和周围的一个曲面组成的。
圆柱的两个圆面叫做底面。它们是两个完全一样的圆。
形状相同,大小相等
周围的(这一个)曲面叫做侧面。
两个底面之间的距离叫做圆柱的高
圆柱的侧面沿高剪下,展开后是一个长方形。议一议,这个长方形的长、宽与圆柱的什么有关?有什么关系?为什么?
长
宽
这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
1、圆柱的表面积指的是什么?
2、圆柱的表面积怎样计算?为什么?
围成圆柱所有面的总面积叫做圆柱的表面积。
长
宽
圆柱的表面积=
侧面积+底面积
×2
因为圆柱的侧面沿高剪下,展开后是一个长方形。这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
所以:
长方形的面积
圆柱的侧面积
= 长 × 宽
底面周长
高
= ×
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
S表面积=2πr×h + 2×πr2
深入认识:
圆柱的表面由上、下两个底面和一个侧面组成的立体图形。
1 一个圆柱的高是15厘米,底面半径是5厘米,它的表面积是多少?
(1)侧面积:
2×3.14×5×15=471(平方厘米)
(2)底面积:3.14× =78.5(平方厘米)
(3)表面积:471+78.5×2=628(平方厘米)
答:它的表面积是628平方厘米。
新知讲解:
2、 一个圆柱,底面直径是5厘米,高是4厘米,求它的表面积是多少
答:它的表面积是102.05平方厘米.
(1)侧面积:
(2)底面积:
(3)表面积:
3.14×5×4 = 62.8(平方厘米)
3.14×( ) = 19.625(平方厘米)
62.8+ 19.625 ×2 =102.05 (平方厘米)
圆柱的表面积=侧面积+底面面积×2
新知讲解:
3. 一个圆柱,底面周长是94.2厘米,高是25厘米,求它的侧面积。
5. 砌一个圆柱形沼气池,底面直径是4米,深是2米。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?
94.2×25=235.5(平方厘米)
4. 一个圆柱,底面直径是2分米,高是45分米,求它的表面积。
3.14×2×45+3.14×12×2
=282.6+6.28
=288.88(平方分米)
3.14×4×2+3.14×22
=25.12+12.56
=37.68(平方米)
答:抹水泥的面积是37.68平方米。
6.求下列圆柱体的表面积
(1)底面半径是4米,高是6米;
(2)底面直径是6分米,高是12分米。
(3)底面周长是25.12厘米,高是8厘米。
表:50.24×2+150.72=251.2(m2)
侧:6×(4×2×3.14)=150.72(m2)
底:42×3.14=50.24(m2)
表:28.26×2+226.08= 282.6 (m2)
侧:12×(6×3.14)=226.08(m2)
底:(6÷2)2×3.14=28.26(m2)
表:50.24×2+200.96= 301.44(m2)
侧:8×25.12=200.96(m2)
底:(25.12÷3.14÷2)2×3.14=50.24(m2)
新知讲解:
1、一顶圆柱形厨师帽,高28㎝,冒顶直径是20 ㎝,做一顶帽子需要多少面料?(得数保留整十平方厘米)
(1)、帽子的侧面积:
3.14×20×28=1758.4(平方厘米)
(2)、帽顶的面积:
3.14×(20÷2)=314(平方厘米)
(3)、需要用的面料:
1758.4+ 314 =2072.4(平方厘米)
≈2070(平方厘米)
答:需要用2070平方厘米的面料。
(1)、帽子的侧面积:
3.14×20×28=1758.4(平方厘米)
(2)、帽顶的面积:
3.14×(20÷2)=314(平方厘米)
(3)、需要用的面料:
1758.4+ 314 =2072.4(平方厘米)
≈2080(平方厘米)
答:需要用2080平方厘米的面料。
注意:今后在计算原材料得数要求取近似数时,为了保证材料的够用,不能用四舍五入法,而必须用进一法。
2. 一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米? (得数保留整百)
(1)侧面积:
3.14×20×24=1507.2(平方厘米)
(2)底面积:3.14× =314(平方厘米)
(3)表面积:1507.2+314=1821.2
答:做这个水桶要用铁皮约1900平方厘米。
≈1900(平方厘米)
新知讲解:
3、 一个没有盖的圆柱形纸盒,底面直径是5厘米,高是4厘米,做这个纸盒要用纸皮多少平方厘米?(得数保留整十平方厘米)
(3)需要纸皮:
≈90(平方厘米)
(1)纸盒侧面积:
(2)纸盒底面积:
答:做这个纸盒要用纸皮 90平方厘米
约
3.14×5×4 =62.8(平方厘米)
3.14×( ) = 19.625(平方厘米)
62.8+ 19.625 = 82.425
尝试练习:
4.一个没有盖的圆柱形铁皮水桶,高是24分米,底面直径是高的 ,做这个水桶要用铁皮多少平方分米?(得数保留整百平方分米)
(1) 底 面 直 径: 24× =20(分米)
(2)水桶的侧面积: 3.14×20×24 =1507.2(平方分米)
(4)需要铁皮: 1507.2+ 314 = 1821.2≈1900(平方分米)
答:做这个水桶用铁皮约1900平方分米。
(3)水桶的底面积: 3.14×( ) =314(平方分米)
尝试练习:
(1)侧面积:2 ×3.14 ×2 ×4.5=56.52 (c㎡)
(2)底面积:3.14 ×22 =12.56 (c㎡)
(3)表面积:56.52+12.56 × 2=81.64 (c㎡)
尝试练习:
1、计算下面图形的表面积。
12cm
16cm
5cm
20cm
1
2
3.14×12×16=226.08(c㎡)
3.14×5×20 =314(c㎡)
我叫
圆柱
我的高
是 4 厘米
我的底面周长
是 12.56 厘米
你们能帮我算出表面积吗?
帮一帮
尝试练习:
现在有一个罐头厂计划用铁皮制作一批底面半径5厘米,高10厘米的圆柱形罐头盒。你能不能帮厂长算一算制作一个至少需要多少平方厘米铁皮?
应用与实践
6.28
2
2
4
4
3
3
2
4
3
轻松一刻
A
B
C
下面哪个图形是圆柱的展开图?
15
3
请帮下面的长方形找底面,使它们能组成圆柱.(单位:厘米)
9.42
r=1.5
( )
r=3
( )
×
√
1、做一个圆柱形的汽油桶,底面直径0.6米,高1米,做这样一个汽油桶大约需要多少平方米的铁皮
2、做一个圆柱形通风管,长2米,管口半径5厘米,做这样一个通风管至少需要多少平方米铁皮
3、一个圆柱形的汽油桶,从里面量,底面直径是40厘米,高1.2米。做这个油桶至少需要多少铁皮?
4、有一根长3.5米的圆柱子,它的底面周长是12.56米。如果给这个圆柱的侧面刷一层漆。刷漆的面积是多少平方米?
5、一节圆柱形烟筒,底面直径是8厘米,长1.5米,做1000节这样的烟筒至少需要用白铁皮多少平方米?
6、一个圆柱,底面周长是94.2厘米,高是25厘米,求它的侧面积。
7、学校食堂要用铁皮做一根横截面半径是3分米,高是3米的圆柱形烟囱,至少需要多少平方米的铁皮?
8、修建一个圆柱形沼气池,底面直径是4米,深是2米。在池的四壁与底面抹上水泥,抹水泥部分的面积是多少平方米?
9、小明做了一个笔筒,他想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸
10.制作一个底面直径20厘米、长50厘米的圆柱形通风管,至少要用多少平方厘米的铁皮?
判断:(对的打“√”,错的打“×”
(1)圆柱体只有一条高。 ( )
(2)圆柱体的侧面积总比表面积小。 ( )
(3)制作一个铁皮烟囱,所用的铁皮面积求圆柱就是侧面积。 ( )
(4)圆柱的侧面是一个平行四边形。 ( )
(5)如果一个圆柱体的侧面展开后是一个正方形,那么圆柱的高是底面半径的2Π倍.( )
√
×
×
√
×
做一个无盖锅所需铁皮面积
说一说该求哪部分的面积
做茶叶桶所需铁皮面积
商标纸面积
求下列圆柱形物体用料的面积,应计算哪些面的总面积?
铁片制成的糖果盒
玻璃杯
铁皮油桶
侧面+2个底面
侧 面
侧面+1个底面
侧 面
侧面+2个底面
塑料制成的水管
水泥烟囱
我来解决生活中的问题
(1)把一个圆柱体侧面展开, 可能得到一个长方形, 这个长方形的长等于圆柱的( ), 宽等于圆柱的( )。
(2)压路机滚动一周能压多少路面是求( )的面积。
(3)做一个无盖的圆柱形水桶,所用铁皮多少,用( )面积加上( )个底面面积。
(4)一支(圆柱形)铅笔,求它需要涂漆的部分,是计算它的( )面积,用底面的( )乘以( )。
圆柱侧面
侧面
一个
侧面
周长
高
口答下列各题
底面周长
高
1.冬天护林工人给圆柱形的树干的下端涂防蛀涂料,那么粉刷树干的面积是指( ).
A.底面积 B.侧面积
C.表面积 D.体积
B
小结:
在解答实际问题前一定要
先进行分析,看它们求的
是哪部分面积,再选择解
答的方法。
1、一个没有盖的圆柱形铁皮水桶,高是48厘米,底面直径是30厘米,做这个水桶至少要用铁皮多少平方厘米?(得数保留整百平方厘米)。
(1)水桶的侧面积:
3.14 ×30 ×48=4521.6(平方厘米)
(2)水桶的底面积:
3.14 ×(30/2) 2 =3.14 ×15 2 =3.14 ×225=706.5(平方厘米)
(3)需要铁皮:
4521.6+706.5=5228.1≈5300(平方厘米)
2.砌一个圆柱形的沼气池,底面直径是3米,
深是2米,在池的周围与底面抹上水泥,
抹上水泥的部分面积是多少平方米?
思考题
1. 一个圆柱体的侧面展开是个边长9.42厘米的正方形,这个圆柱体的表面积是多少平方厘米?(得数保留两位小数)
9.42×9.42+3.14×(9.42÷3.14)2×2
=88.728+14.13
≈102.86(平方厘米)
答:这个圆柱体的表面积是102.86平方厘米。
2. 一个圆柱体的侧面积是226.08平方厘米,底面半径4厘米,它的高是多少?
226.08÷(2×3.14×4)
=226.08÷25.12
=9(厘米)
答:它的高是9厘米。
3. 把一段长20分米的圆柱形木头沿着底面直径劈开,表面积增加80平方分米,原来这段圆柱形木头的表面积是多少?
4.砌一个圆柱形水池,底面周长是25.12米,深2米,要在它的底面和四周抹上水泥,如果每平方米用水泥10千克,共需水泥多少千克?
80÷2=40(平方分米)(一个长方形面积)
40÷20=2(分米)(底面直径)
2×3.14×20=125.6(平方分米) (侧面积)
3.14×(2÷2) ×2=6.28(平方分米)(底面积和)125.6+6.28=131.88(平方分米)(表面积)
答:原来这段圆柱形木头的表面积是131.88平方分米。
(1)求底面面积:3.14×4×4=50.24(平方米)
(2)侧面积:25.12×2=50.24(平方米)
(3)总面积: 50.24+50.24=100.48(平方米)
(4)共需水泥:100.48×10=100.48 (千克)
答:共需水泥1004.8千克。
圆的半径:25.12÷3.14÷2=4(米)
1、把一个底面直径是16分米,高15分米的圆柱,分成四个小圆柱,表面积比原来增加了多少平方分米?
2、一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)
3、将一个圆柱的侧面展开,得到一个边长是15、7厘米的正方形。求原来圆柱的侧面积。
4、做50节同样大小的圆柱形通风管,每节长4米,管口直径是10厘米,至少需要多少平方米的铁皮?
5、压路机的滚筒是一个圆柱形,它的宽是1、5米,滚筒横截面的半径是0、6米,以每分钟滚动5周计算,每分钟压路的面积是多少平方米?
1、圆柱的高是15.7厘米,侧面展开是个正方形,圆柱的侧面积是多少平方厘米?
2、圆柱的高是15.7厘米,侧面展开是个正方形,圆柱的表面积是多少平方厘米?
3、大厅里有8根圆柱形柱子,每根的底面直径4分米,高3米,如果每平方米需油漆费0.5元,漆这8根柱子约需要油漆费多少元?
4、把一个底面半径是7分米,高15分米的圆柱沿着垂直于底面分为两个半圆柱,表面积增加了多少平方分米?
5、一个圆柱的侧面积是188.4平方分米,底面半径是2分米,它的高是多少分米
我来做裁判.
1、求下面各圆柱的表面积。
(1)底面直径是12厘米,高是16厘米。
3.14×12×16+3.14×( ) ×2 ( )
(2)底面半径是5分米,高是20分米。
2×3 .14× 5×20+ 3 .14× 5 ( )
√
×
2、圆柱的侧面展开后一定是长方形. ( )
3、做一个无盖的圆柱水桶,需要的铁皮的
面积是圆柱的表面积。 ( )
4、一个圆柱的底面半径扩大4倍,高不变,
它的侧面积就扩大16倍.( )
√
×
×
20π厘米
15π厘米
它们的表面积相等吗
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
分两种情况:
1、以20π厘米为底面周长,10 π厘米为高。
2、以10 π厘米为底面周长 ,20 π厘米为高。
10 π
20π
20 π
10π
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以20π厘米为底面周长,10 π厘米为高。
解:C=20 π厘米,
h=10 π厘米
S侧=Ch
=20 π×10 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=10(cm)
S底= πr2=100 π(cm2)
S表=S侧+2S底=(200 π2+200 π )cm2
20π
10π
答:这个圆柱的表面积为(200π2+200π)cm2或(200π2+50π)cm2
一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
以10π厘米为底面周长,20 π厘米为高。
解:C=10 π厘米,
h=20 π厘米
S侧=Ch
=10 π×20 π
=200 π2(cm2)
因为C=2 πr
所以 r=C/(2π)
=5(cm)
S底= πr2=25 π(cm2)
S表=S侧+2S底=(200 π2+50 π )cm2
10π
20π
动脑筋
10
S侧=3.14 × 6 × 10=188.4(cm2)
下面两个圆柱体的侧面积、表面积是否相等?(单位:厘米)
10
6
6
S底=3.14 × (6/2)2=28.26(cm2)
S表=S侧+2S底=244.92(cm2)
S侧=3.14 × 10 × 6=188.4(cm2)
S底=3.14 × (10/2)2=78.5(cm2)
S表=S侧+2S底=345.4(cm2)
两个圆柱的侧面积相等,表面积不相等。
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
3、一根圆柱形木料长20dm,把它截成4个相等的小段, 表面积增加了18.84d㎡。横截面的面积是 ( )
3.14d㎡
4、一根长2米、底面直径是4厘米的圆柱形木料,把它锯成同样长的4段,表面积比原来增加了( )平方厘米。
动脑筋
5、如图:把一个底面是6cm2,高4cm的圆柱沿着高切开,分成3个小圆柱,它的表面积增加( )cm2.
A、12
B、18
C、24
D、36
C
1、把一个底面直径为5厘米,高是8厘米的圆柱体沿底面直径切开,分成形状大小完全相同的两部分,它们的表面积比原来增加多少平方厘米?
动脑筋
有一根圆柱形的木材,底面直径是16厘米,高是20厘米沿着它的底面直径, 从上向下锯成相等的两块(如图),每块的表面积是多少
动脑筋
2、李师傅把一根高1米的圆柱形木料,沿底面直径平均分成两部分,这时表面积比原来增加了0.8平方米。求这根木料原来的表面积。
(1)底面直径: 0.8 ÷2 ÷1=0.4 (m)
(2)圆柱的表面积:
3.14×(0.4÷2)×2+3.14×0.4×1
=0.2512+1.256
=1.5072(平方米)
答:这根木料原来的表面积是1.5072平方米。
挑战自我
把一个高10厘米的圆柱,按下图切开,拼成一个近似的长方体。表面积就增加了( )平方厘米.
60
挑战自我
1、一个圆柱体的侧面积是72π cm2,底面半径4 cm,它的高是多少?
解:72π÷(2×π×4)
=72π÷8π
=9(cm)
答:它的高是9 cm。
2、一个圆柱体的侧面展开是个边长9.42 cm的 正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
解:9.42×9.42+3.14(9.42÷3.14÷2)2×2
=88.728+14.13
≈102.86( cm2 )
答:这个圆柱体的表面积是102.86 cm2。
挑战自我
挑战自我
用一个棱长是6分米的正方体,削成一个最大的圆柱体,这个圆柱的表面积是多少?
左图是一个圆柱形状的蛋糕盒,底面半径15厘米,高20厘米。
(1)做这个蛋糕盒大约需要用多少平方厘米的纸板?
(2)像左图那样用彩带包扎这个蛋糕盒,至少需要彩带多少厘米?(打结处大约用15厘米彩带)
运用知识解决问题
全课总结
