人教版数学九年级上册22.2二次函数与一元二次方程的关系 教案(无答案)
文档属性
| 名称 | 人教版数学九年级上册22.2二次函数与一元二次方程的关系 教案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 107.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 00:00:00 | ||
图片预览

文档简介
课题:《二次函数与一元二次方程的关系》
【学习目标】
1、通过探索,理解二次函数与一元二次方程的联系
2、运用二次函数及其图象、性质解一元二次方程
【评价目标】
1. 自我检查:能判断二次函数与一元二次方程的关系
2. 对话展示:能选择数形结合的方法解一元二次方程
3. 课堂提问:能辨别函数值与方程的解的转化
4. 纸笔作业:能用数形结合的思想求一元二次方程出方程的解
【重点难点】
学习重点 : 理解二次函数与一元二次方程的联系
学习难点 : 数形结合的思想
【教学过程】
一、【温故·习新】
预习作业
1.问题:如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h=20t-5t2. 考虑以下问题:
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地要用多少时间?
探索新知
1.观察图象:
(1)二次函数y=x2+x-2的图象与x轴有____个交点,则一元二次方程x2+x-2=0的根的判别式△=_______0;
(2)二次函数y=x2-6x+9的图像与x轴有___________个交点,则一元二次方程
x2-6x+9=0的根的判别式△=_______0;
(3)二次函数y=x2-x+1的图象与x轴________公共点,则一元二次方程x2-x+1=0的根的判别式△_______0.
2.归纳:
(1)如果抛物线与x轴有公共点,公共点的横坐标是,那么当时,函数值是________,因此是方程________________的一个根.
(2)已知二次函数y=-x2+4x的函数值为3,求自变量x的值,可以看作解一元二次方程 __________________.反之,解一元二次方程-x2+4x=3又可以看作已知二次函数 __________________的函数值为3的自变量x的值.
一般地:已知二次函数y=ax2+bx+c的函数值为m,求自变量x的值,可以看作解一元二次方程ax2+bx+c=m.反之,解一元二次方程ax2+bx+c=m又可以看作已知二次函数y=ax2+bx+c的值为m的自变量x的值.
(3)二次函数y=ax2+bx+c与x轴的位置关系:
一元二次方程ax2+bx+c=0的根的判别式△=b2-4ac.
(1)当△=b2-4ac>0时 抛物线y=ax2+bx+c与x轴有_______交点;
(2)当△=b2-4ac=0时 抛物线y=ax2+bx+c与x轴_______交点;
(3)当△=b2-4ac<0时 抛物线y=ax2+bx+c与x轴_______公共点.
二、【研讨·拓展】
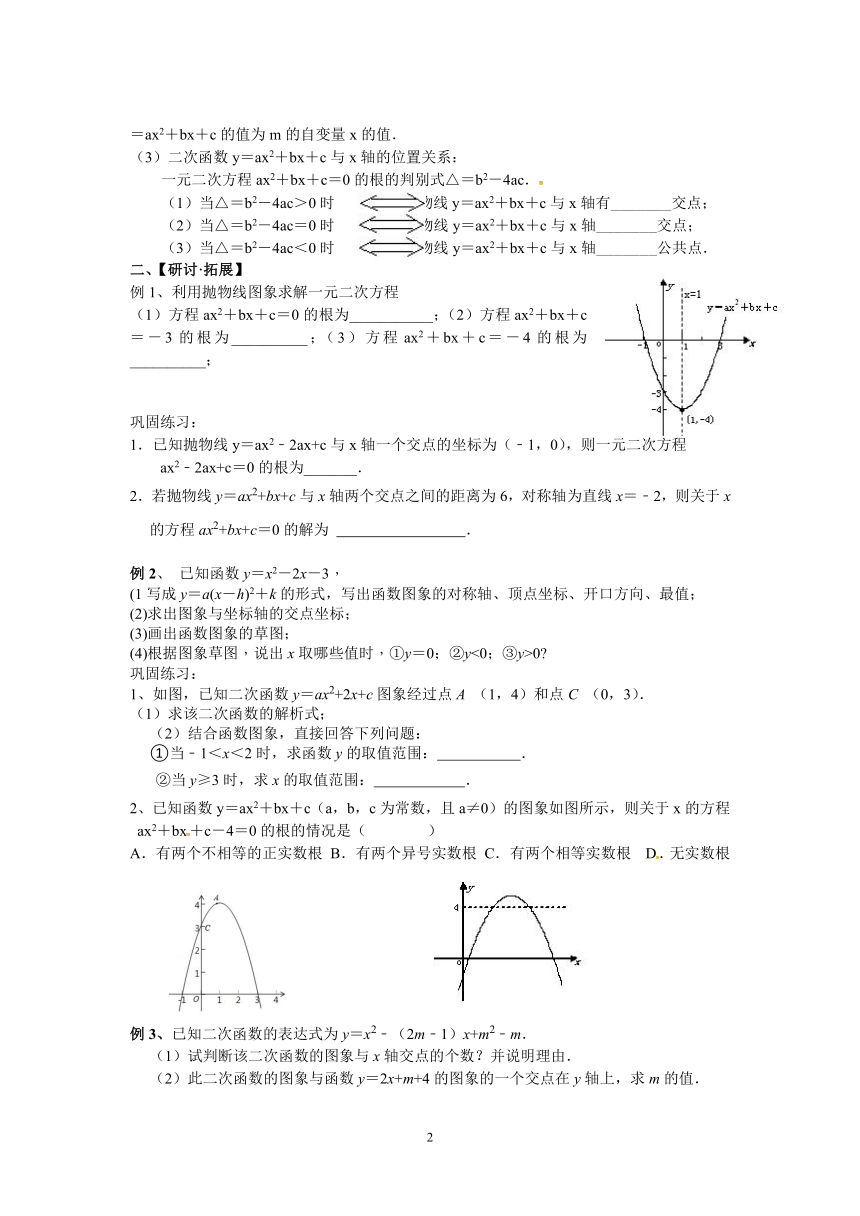
例1、利用抛物线图象求解一元二次方程
(1)方程ax2+bx+c=0的根为___________;(2)方程ax2+bx+c=-3的根为__________;(3)方程ax2+bx+c=-4的根为__________;
巩固练习:
已知抛物线y=ax2﹣2ax+c与x轴一个交点的坐标为(﹣1,0),则一元二次方程
ax2﹣2ax+c=0的根为_______.
2.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为6,对称轴为直线x=﹣2,则关于x的方程ax2+bx+c=0的解为 .
例2、 已知函数y=x2-2x-3,
(1写成y=a(x-h)2+k的形式,写出函数图象的对称轴、顶点坐标、开口方向、最值;
(2)求出图象与坐标轴的交点坐标;
(3)画出函数图象的草图;
(4)根据图象草图,说出x取哪些值时,①y=0;②y<0;③y>0
巩固练习:
1、如图,已知二次函数y=ax2+2x+c图象经过点A (1,4)和点C (0,3).
(1)求该二次函数的解析式;
(2)结合函数图象,直接回答下列问题:
①当﹣1<x<2时,求函数y的取值范围: .
②当y≥3时,求x的取值范围: .
2、已知函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,则关于x的方程
ax2+bx+c-4=0的根的情况是( )
有两个不相等的正实数根 B.有两个异号实数根 C.有两个相等实数根 D.无实数根
例3、已知二次函数的表达式为y=x2﹣(2m﹣1)x+m2﹣m.
(1)试判断该二次函数的图象与x轴交点的个数?并说明理由.
(2)此二次函数的图象与函数y=2x+m+4的图象的一个交点在y轴上,求m的值.
巩固练习:
1.已知:二次函数y=kx2﹣3x﹣3的图象与x轴有两个交点,则k的取值范围为 .
2.若函数y=mx2-x+1与x轴有两个交点,求m的范围
3.已知抛物线y=kx2+2x-1与坐标轴有三个交点,则k的取值范围___________.
三、【反馈·提炼】
1、二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:①abc<0;②a﹣b+c>0;③c﹣4a=1;④b2>4ac;⑤am2+bm+c≤1(m为任意实数).其中正确的有( )A.2个 B.3个 C.4个 D.5个
2、抛物线y=ax2+ax+1的一部分如下图一所示,那么该抛物线在y轴右侧与x轴交点的坐标是( )A.(0,0) B.(1,0) C.(2,0) D.(2.5,0)
3、如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:
①abc<0;②3a+b>0;③4a﹣2b+c>0;④b2=4a(c﹣n);
⑤一元二次方程ax2+bx+c=n+1有两个互异实根.其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
4、关于x的一元二次方程ax2﹣3x﹣1=0的两个不相等的实数根都在﹣1和0之间(不包括﹣1和0),则a的取值范围是
【课堂小结】.
本节课的思维导图
每日一题:
【每日一题】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣2.5 ﹣2 ﹣1 0 1 2 2.5 3 …
y … 3 1.25 m ﹣1 0 ﹣1 0 1.25 3 …
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出1条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.
③函数y=x2﹣2|x|的图象与y=a有至少有3个交点时,a的取值范围是 .
二次函数与X轴的交点个数
根据函数图像求一元二次方程的近似解
如果抛物线与X轴的交点坐标(x1,0),(x2,0),那么x1,x2就是方程的解
二次函数与一元二次方程的关系
二次函数与一元二次方程
PAGE
1
【学习目标】
1、通过探索,理解二次函数与一元二次方程的联系
2、运用二次函数及其图象、性质解一元二次方程
【评价目标】
1. 自我检查:能判断二次函数与一元二次方程的关系
2. 对话展示:能选择数形结合的方法解一元二次方程
3. 课堂提问:能辨别函数值与方程的解的转化
4. 纸笔作业:能用数形结合的思想求一元二次方程出方程的解
【重点难点】
学习重点 : 理解二次函数与一元二次方程的联系
学习难点 : 数形结合的思想
【教学过程】
一、【温故·习新】
预习作业
1.问题:如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系h=20t-5t2. 考虑以下问题:
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地要用多少时间?
探索新知
1.观察图象:
(1)二次函数y=x2+x-2的图象与x轴有____个交点,则一元二次方程x2+x-2=0的根的判别式△=_______0;
(2)二次函数y=x2-6x+9的图像与x轴有___________个交点,则一元二次方程
x2-6x+9=0的根的判别式△=_______0;
(3)二次函数y=x2-x+1的图象与x轴________公共点,则一元二次方程x2-x+1=0的根的判别式△_______0.
2.归纳:
(1)如果抛物线与x轴有公共点,公共点的横坐标是,那么当时,函数值是________,因此是方程________________的一个根.
(2)已知二次函数y=-x2+4x的函数值为3,求自变量x的值,可以看作解一元二次方程 __________________.反之,解一元二次方程-x2+4x=3又可以看作已知二次函数 __________________的函数值为3的自变量x的值.
一般地:已知二次函数y=ax2+bx+c的函数值为m,求自变量x的值,可以看作解一元二次方程ax2+bx+c=m.反之,解一元二次方程ax2+bx+c=m又可以看作已知二次函数y=ax2+bx+c的值为m的自变量x的值.
(3)二次函数y=ax2+bx+c与x轴的位置关系:
一元二次方程ax2+bx+c=0的根的判别式△=b2-4ac.
(1)当△=b2-4ac>0时 抛物线y=ax2+bx+c与x轴有_______交点;
(2)当△=b2-4ac=0时 抛物线y=ax2+bx+c与x轴_______交点;
(3)当△=b2-4ac<0时 抛物线y=ax2+bx+c与x轴_______公共点.
二、【研讨·拓展】
例1、利用抛物线图象求解一元二次方程
(1)方程ax2+bx+c=0的根为___________;(2)方程ax2+bx+c=-3的根为__________;(3)方程ax2+bx+c=-4的根为__________;
巩固练习:
已知抛物线y=ax2﹣2ax+c与x轴一个交点的坐标为(﹣1,0),则一元二次方程
ax2﹣2ax+c=0的根为_______.
2.若抛物线y=ax2+bx+c与x轴两个交点之间的距离为6,对称轴为直线x=﹣2,则关于x的方程ax2+bx+c=0的解为 .
例2、 已知函数y=x2-2x-3,
(1写成y=a(x-h)2+k的形式,写出函数图象的对称轴、顶点坐标、开口方向、最值;
(2)求出图象与坐标轴的交点坐标;
(3)画出函数图象的草图;
(4)根据图象草图,说出x取哪些值时,①y=0;②y<0;③y>0
巩固练习:
1、如图,已知二次函数y=ax2+2x+c图象经过点A (1,4)和点C (0,3).
(1)求该二次函数的解析式;
(2)结合函数图象,直接回答下列问题:
①当﹣1<x<2时,求函数y的取值范围: .
②当y≥3时,求x的取值范围: .
2、已知函数y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,则关于x的方程
ax2+bx+c-4=0的根的情况是( )
有两个不相等的正实数根 B.有两个异号实数根 C.有两个相等实数根 D.无实数根
例3、已知二次函数的表达式为y=x2﹣(2m﹣1)x+m2﹣m.
(1)试判断该二次函数的图象与x轴交点的个数?并说明理由.
(2)此二次函数的图象与函数y=2x+m+4的图象的一个交点在y轴上,求m的值.
巩固练习:
1.已知:二次函数y=kx2﹣3x﹣3的图象与x轴有两个交点,则k的取值范围为 .
2.若函数y=mx2-x+1与x轴有两个交点,求m的范围
3.已知抛物线y=kx2+2x-1与坐标轴有三个交点,则k的取值范围___________.
三、【反馈·提炼】
1、二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:①abc<0;②a﹣b+c>0;③c﹣4a=1;④b2>4ac;⑤am2+bm+c≤1(m为任意实数).其中正确的有( )A.2个 B.3个 C.4个 D.5个
2、抛物线y=ax2+ax+1的一部分如下图一所示,那么该抛物线在y轴右侧与x轴交点的坐标是( )A.(0,0) B.(1,0) C.(2,0) D.(2.5,0)
3、如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,则下列结论:
①abc<0;②3a+b>0;③4a﹣2b+c>0;④b2=4a(c﹣n);
⑤一元二次方程ax2+bx+c=n+1有两个互异实根.其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
4、关于x的一元二次方程ax2﹣3x﹣1=0的两个不相等的实数根都在﹣1和0之间(不包括﹣1和0),则a的取值范围是
【课堂小结】.
本节课的思维导图
每日一题:
【每日一题】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x … ﹣3 ﹣2.5 ﹣2 ﹣1 0 1 2 2.5 3 …
y … 3 1.25 m ﹣1 0 ﹣1 0 1.25 3 …
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出1条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.
③函数y=x2﹣2|x|的图象与y=a有至少有3个交点时,a的取值范围是 .
二次函数与X轴的交点个数
根据函数图像求一元二次方程的近似解
如果抛物线与X轴的交点坐标(x1,0),(x2,0),那么x1,x2就是方程的解
二次函数与一元二次方程的关系
二次函数与一元二次方程
PAGE
1
同课章节目录
