2025人教B版高中数学必修第四册强化练习题(含解析)--专题强化练6 空间角的有关计算
文档属性
| 名称 | 2025人教B版高中数学必修第四册强化练习题(含解析)--专题强化练6 空间角的有关计算 |
|
|
| 格式 | docx | ||
| 文件大小 | 405.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 11:00:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第四册
专题强化练6 空间角的有关计算
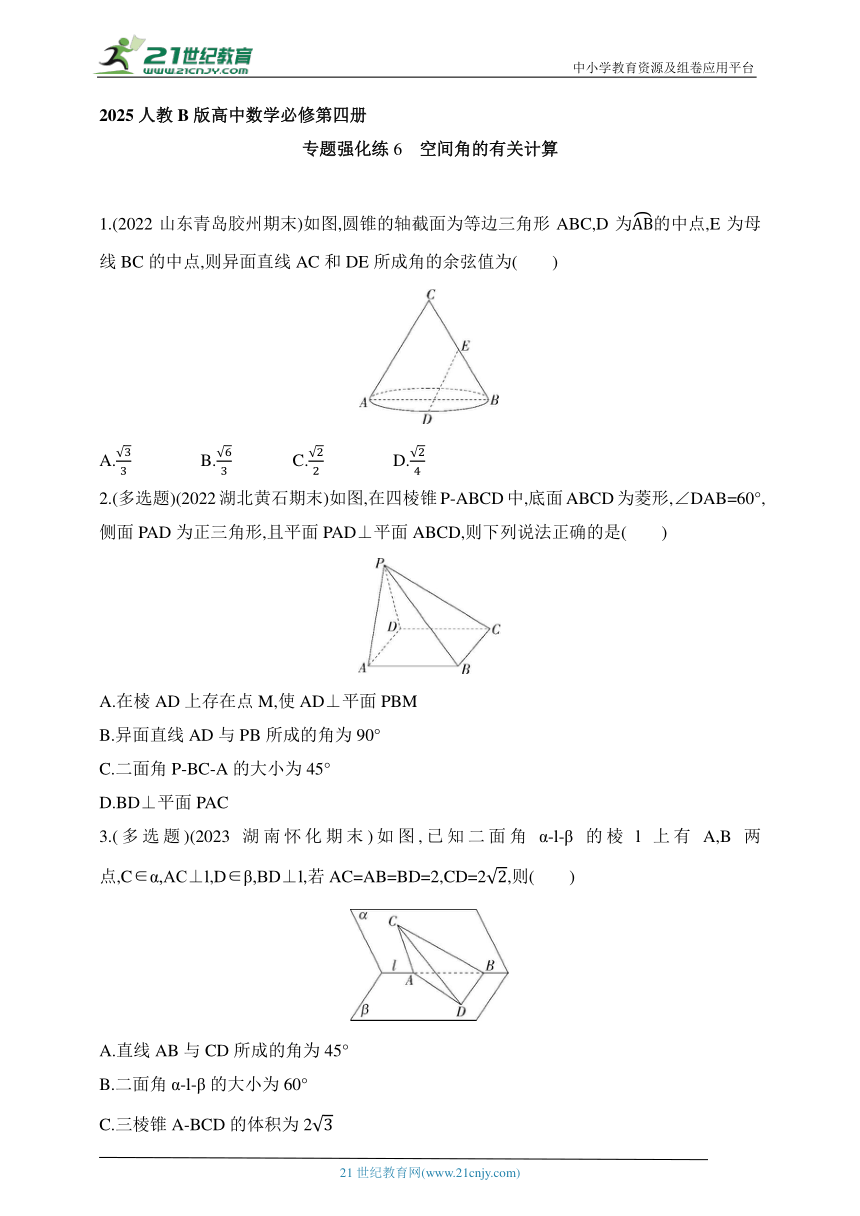
1.(2022山东青岛胶州期末)如图,圆锥的轴截面为等边三角形ABC,D为的中点,E为母线BC的中点,则异面直线AC和DE所成角的余弦值为( )
A. B. C. D.
2.(多选题)(2022湖北黄石期末)如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法正确的是( )
A.在棱AD上存在点M,使AD⊥平面PBM
B.异面直线AD与PB所成的角为90°
C.二面角P-BC-A的大小为45°
D.BD⊥平面PAC
3.(多选题)(2023湖南怀化期末)如图,已知二面角α-l-β的棱l上有A,B两点,C∈α,AC⊥l,D∈β,BD⊥l,若AC=AB=BD=2,CD=2,则( )
A.直线AB与CD所成的角为45°
B.二面角α-l-β的大小为60°
C.三棱锥A-BCD的体积为2
D.直线CD与平面β所成角的正弦值为
4.(2022河北衡水第十四中学期末)如图,已知二面角A-BC-D,AB=2,BC=2,CD=,AD=,且AB⊥BC,CD⊥BC,则二面角A-BC-D的余弦值为 .
5.(2024重庆高考模拟调研卷)在如图所示的四棱锥P-ABCD中,已知AB∥CD,∠BAD=90°,CD=2AB,△PAB是正三角形,点M在侧棱PB上,且PD∥平面AMC.
(1)证明:PM=2BM;
(2)若侧面PAB⊥底面ABCD,CM与底面ABCD所成角的正切值为,求二面角P-AC-B的余弦值.
答案与分层梯度式解析
1.C 设等边三角形ABC的边长为2,AB的中点为O,连接OC,OD,OE,如图所示,
因为E是BC的中点,所以OE∥AC,OE=AC=1,
则∠OED(或其补角)是异面直线AC和DE所成的角,
因为D为的中点,所以OD⊥AB,
又OC⊥OD,OC∩AB=O,OC,AB 平面ABC,
所以OD⊥平面ABC,又OE 平面ABC,
所以OD⊥OE,
在Rt△ODE中,cos∠OED===.
故选C.
2.ABC 如图,取AD的中点M,连接PM,BM,BD,
∵侧面PAD为正三角形,∴PM⊥AD,
又底面ABCD是菱形,∠DAB=60°,
∴△ABD是等边三角形,
又M为AD的中点,∴BM⊥AD,
又PM∩BM=M,PM,BM 平面PBM,
∴AD⊥平面PBM,故A中说法正确.
∵AD⊥平面PBM,PB 平面PBM,
∴AD⊥PB,即异面直线AD与PB所成的角为90°,故B中说法正确.
∵AD⊥平面PBM,BC∥AD,∴BC⊥平面PBM,
又PB,BM 平面PBM,∴BC⊥PB,BC⊥BM,
又平面PBC∩平面ABCD=BC,
∴∠PBM是二面角P-BC-A的平面角,
设AB=1,则BM=,PM=,在Rt△PBM中,
tan∠PBM==1,即∠PBM=45°,故二面角P-BC-A的大小为45°,故C中说法正确.
因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PM 平面PAD,PM⊥AD,
所以PM⊥平面ABCD,
又BD 平面ABCD,所以PM⊥BD.
连接AC,假设BD⊥平面PAC,则有BD⊥PA,
又PM∩PA=P,PM,PA 平面PAD,
所以BD⊥平面PAD,又AD 平面PAD,所以BD⊥AD,
而由题可知,BD与AD的夹角为60°,矛盾,故假设不成立,故D中说法错误.故选ABC.
3.ABD 如图,在β内作DE∥AB,AE∥BD,AE与DE交于点E,
则∠CDE(或其补角)即为直线AB与CD所成的角,
因为BD⊥l,AB=BD=2,所以AE⊥AB,ED⊥BD,
故四边形AEDB为正方形,所以DE⊥AE,
又AC⊥l,所以DE⊥AC,
又AC∩AE=A,AC,AE 平面ACE,
所以DE⊥平面ACE,
又CE 平面ACE,所以DE⊥CE,
又CD=2,DE=AB=2,所以cos∠CDE==,
因为0°<∠CDE<90°,所以∠CDE=45°,故A正确;
因为AC⊥AB,EA⊥AB,
所以∠CAE为二面角α-l-β的平面角,
由以上分析可知CE===2,AE=BD=2,又AC=2,所以△ACE为正三角形,
所以∠CAE=60°,故B正确;
因为DE⊥平面ACE,DE 平面AEDB,所以平面ACE⊥平面AEDB,且平面ACE∩平面AEDB=AE,故作CH⊥AE,垂足为H,
则CH⊥平面AEDB,且CH=ACsin 60°=,
所以VA-BCD=VC-ABD=S△ABD·CH=××2×2×=,故C错误;
连接DH,因为CH⊥平面AEDB,所以∠CDH为直线CD与平面β所成的角,在Rt△CHD中,sin∠CDH===,故D正确.
故选ABD.
4.答案
解析 如图,过点B作BE∥CD,过点D作DE∥BC,且BE∩DE=E,易知四边形BCDE为矩形,
∴BE=CD=,BE⊥BC,
又AB⊥BC,AB∩BE=B,AB,BE 平面ABE,
∴BC⊥平面ABE,
∴∠ABE是二面角A-BC-D的平面角,易得DE⊥平面ABE,
又AE 平面ABE,∴DE⊥AE,
在Rt△ADE中,DE=BC=2,AD=,故AE==,
在△ABE中,AB=2,
∴cos∠ABE===.
5.解析 (1)证明:连接BD与AC交于点E,连接EM,
易知△EAB∽△ECD,∴=,
由CD=2AB,得ED=2EB,又∵PD∥平面AMC,
而平面PBD∩平面AMC =ME,PD 平面PBD,
∴PD∥EM,
∴在△PBD中,==,
∴PM=2BM.
(2)设AB的中点为O,连接PO,易知PO⊥AB,
∵侧面PAB⊥底面ABCD,侧面PAB∩底面ABCD=AB,且PO 平面PAB,∴PO⊥底面ABCD,
过点M作MF∥PO,交AB于点F,
∴MF⊥底面ABCD,连接CF,
∴∠MCF为CM与底面ABCD所成角,
∴=,设AB=6a,则MF=a,
∴CF=11a,BF==a,AF=5a,CD=12a,则AD==6a,
在底面ABCD上过点O作OG⊥AC于点G,连接PG,
则∠PGO是二面角P-AC-B的平面角,易得OA=3a,AC=6a,
在梯形ABCD中,由=得=,得OG=a,
在Rt△POG中,PG=a,
∴cos∠PGO==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第四册
专题强化练6 空间角的有关计算
1.(2022山东青岛胶州期末)如图,圆锥的轴截面为等边三角形ABC,D为的中点,E为母线BC的中点,则异面直线AC和DE所成角的余弦值为( )
A. B. C. D.
2.(多选题)(2022湖北黄石期末)如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法正确的是( )
A.在棱AD上存在点M,使AD⊥平面PBM
B.异面直线AD与PB所成的角为90°
C.二面角P-BC-A的大小为45°
D.BD⊥平面PAC
3.(多选题)(2023湖南怀化期末)如图,已知二面角α-l-β的棱l上有A,B两点,C∈α,AC⊥l,D∈β,BD⊥l,若AC=AB=BD=2,CD=2,则( )
A.直线AB与CD所成的角为45°
B.二面角α-l-β的大小为60°
C.三棱锥A-BCD的体积为2
D.直线CD与平面β所成角的正弦值为
4.(2022河北衡水第十四中学期末)如图,已知二面角A-BC-D,AB=2,BC=2,CD=,AD=,且AB⊥BC,CD⊥BC,则二面角A-BC-D的余弦值为 .
5.(2024重庆高考模拟调研卷)在如图所示的四棱锥P-ABCD中,已知AB∥CD,∠BAD=90°,CD=2AB,△PAB是正三角形,点M在侧棱PB上,且PD∥平面AMC.
(1)证明:PM=2BM;
(2)若侧面PAB⊥底面ABCD,CM与底面ABCD所成角的正切值为,求二面角P-AC-B的余弦值.
答案与分层梯度式解析
1.C 设等边三角形ABC的边长为2,AB的中点为O,连接OC,OD,OE,如图所示,
因为E是BC的中点,所以OE∥AC,OE=AC=1,
则∠OED(或其补角)是异面直线AC和DE所成的角,
因为D为的中点,所以OD⊥AB,
又OC⊥OD,OC∩AB=O,OC,AB 平面ABC,
所以OD⊥平面ABC,又OE 平面ABC,
所以OD⊥OE,
在Rt△ODE中,cos∠OED===.
故选C.
2.ABC 如图,取AD的中点M,连接PM,BM,BD,
∵侧面PAD为正三角形,∴PM⊥AD,
又底面ABCD是菱形,∠DAB=60°,
∴△ABD是等边三角形,
又M为AD的中点,∴BM⊥AD,
又PM∩BM=M,PM,BM 平面PBM,
∴AD⊥平面PBM,故A中说法正确.
∵AD⊥平面PBM,PB 平面PBM,
∴AD⊥PB,即异面直线AD与PB所成的角为90°,故B中说法正确.
∵AD⊥平面PBM,BC∥AD,∴BC⊥平面PBM,
又PB,BM 平面PBM,∴BC⊥PB,BC⊥BM,
又平面PBC∩平面ABCD=BC,
∴∠PBM是二面角P-BC-A的平面角,
设AB=1,则BM=,PM=,在Rt△PBM中,
tan∠PBM==1,即∠PBM=45°,故二面角P-BC-A的大小为45°,故C中说法正确.
因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PM 平面PAD,PM⊥AD,
所以PM⊥平面ABCD,
又BD 平面ABCD,所以PM⊥BD.
连接AC,假设BD⊥平面PAC,则有BD⊥PA,
又PM∩PA=P,PM,PA 平面PAD,
所以BD⊥平面PAD,又AD 平面PAD,所以BD⊥AD,
而由题可知,BD与AD的夹角为60°,矛盾,故假设不成立,故D中说法错误.故选ABC.
3.ABD 如图,在β内作DE∥AB,AE∥BD,AE与DE交于点E,
则∠CDE(或其补角)即为直线AB与CD所成的角,
因为BD⊥l,AB=BD=2,所以AE⊥AB,ED⊥BD,
故四边形AEDB为正方形,所以DE⊥AE,
又AC⊥l,所以DE⊥AC,
又AC∩AE=A,AC,AE 平面ACE,
所以DE⊥平面ACE,
又CE 平面ACE,所以DE⊥CE,
又CD=2,DE=AB=2,所以cos∠CDE==,
因为0°<∠CDE<90°,所以∠CDE=45°,故A正确;
因为AC⊥AB,EA⊥AB,
所以∠CAE为二面角α-l-β的平面角,
由以上分析可知CE===2,AE=BD=2,又AC=2,所以△ACE为正三角形,
所以∠CAE=60°,故B正确;
因为DE⊥平面ACE,DE 平面AEDB,所以平面ACE⊥平面AEDB,且平面ACE∩平面AEDB=AE,故作CH⊥AE,垂足为H,
则CH⊥平面AEDB,且CH=ACsin 60°=,
所以VA-BCD=VC-ABD=S△ABD·CH=××2×2×=,故C错误;
连接DH,因为CH⊥平面AEDB,所以∠CDH为直线CD与平面β所成的角,在Rt△CHD中,sin∠CDH===,故D正确.
故选ABD.
4.答案
解析 如图,过点B作BE∥CD,过点D作DE∥BC,且BE∩DE=E,易知四边形BCDE为矩形,
∴BE=CD=,BE⊥BC,
又AB⊥BC,AB∩BE=B,AB,BE 平面ABE,
∴BC⊥平面ABE,
∴∠ABE是二面角A-BC-D的平面角,易得DE⊥平面ABE,
又AE 平面ABE,∴DE⊥AE,
在Rt△ADE中,DE=BC=2,AD=,故AE==,
在△ABE中,AB=2,
∴cos∠ABE===.
5.解析 (1)证明:连接BD与AC交于点E,连接EM,
易知△EAB∽△ECD,∴=,
由CD=2AB,得ED=2EB,又∵PD∥平面AMC,
而平面PBD∩平面AMC =ME,PD 平面PBD,
∴PD∥EM,
∴在△PBD中,==,
∴PM=2BM.
(2)设AB的中点为O,连接PO,易知PO⊥AB,
∵侧面PAB⊥底面ABCD,侧面PAB∩底面ABCD=AB,且PO 平面PAB,∴PO⊥底面ABCD,
过点M作MF∥PO,交AB于点F,
∴MF⊥底面ABCD,连接CF,
∴∠MCF为CM与底面ABCD所成角,
∴=,设AB=6a,则MF=a,
∴CF=11a,BF==a,AF=5a,CD=12a,则AD==6a,
在底面ABCD上过点O作OG⊥AC于点G,连接PG,
则∠PGO是二面角P-AC-B的平面角,易得OA=3a,AC=6a,
在梯形ABCD中,由=得=,得OG=a,
在Rt△POG中,PG=a,
∴cos∠PGO==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
