2025人教B版高中数学必修第四册强化练习题(含解析)--9.2 正弦定理与余弦定理的应用9.3 数学探究活动得到不可达两点之间的距离
文档属性
| 名称 | 2025人教B版高中数学必修第四册强化练习题(含解析)--9.2 正弦定理与余弦定理的应用9.3 数学探究活动得到不可达两点之间的距离 |

|
|
| 格式 | docx | ||
| 文件大小 | 451.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 11:02:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第四册
第九章 解三角形
9.2 正弦定理与余弦定理的应用
9.3 数学探究活动:得到不可达两点之间的距离
基础过关练
题组一 距离问题
1.如图,已知A,B,C,D四点在同一条直线上,且平面PAD与地面垂直,在山顶P测得点A,C,D的俯角分别为30°,60°,45°,并测得AB=200 m,CD=100 m,现欲沿直线AD开通穿山隧道,则隧道BC的长为( )
A.100(+1)m B.200(+1)m
C.200 m D.100 m
2.(2022陕西渭南期末)在某次海军演习中,已知甲驱逐舰在航母的南偏东15°方向且与航母的距离为12海里,乙护卫舰在甲驱逐舰的正西方向,若测得乙护卫舰在航母的南偏西45°方向,则甲驱逐舰与乙护卫舰之间的距离为( )
A.6海里 B.6海里
C.4海里 D.12海里
3.如图,要测量河对岸A,B两点间的距离,现沿河岸选取相距12 m的C,D两点,测得∠ACB=75°,∠BCD=45°,∠ADB=45°,∠ADC=30°,则A,B两点之间的距离是( )
A.4 m B.4 m C.4 m D.4 m
题组二 高度问题
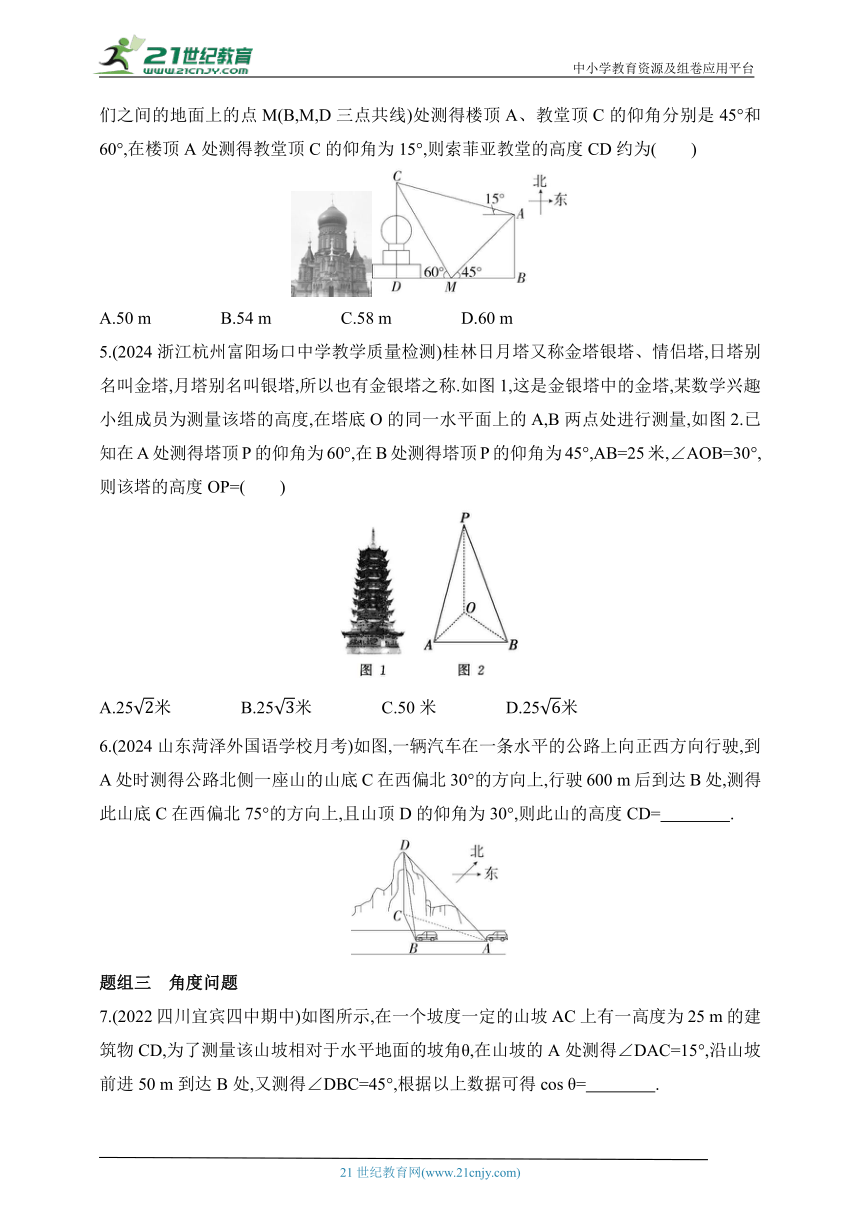
4.(2024福建三明第一中学月考)2023年入冬以来,哈尔滨冰雪旅游火爆出圈.圣·索菲亚教堂是哈尔滨的标志性建筑,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美.为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物AB,高约为36 m,在它们之间的地面上的点M(B,M,D三点共线)处测得楼顶A、教堂顶C的仰角分别是45°和60°,在楼顶A处测得教堂顶C的仰角为15°,则索菲亚教堂的高度CD约为( )
A.50 m B.54 m C.58 m D.60 m
5.(2024浙江杭州富阳场口中学教学质量检测)桂林日月塔又称金塔银塔、情侣塔,日塔别名叫金塔,月塔别名叫银塔,所以也有金银塔之称.如图1,这是金银塔中的金塔,某数学兴趣小组成员为测量该塔的高度,在塔底O的同一水平面上的A,B两点处进行测量,如图2.已知在A处测得塔顶P的仰角为60°,在B处测得塔顶P的仰角为45°,AB=25米,∠AOB=30°,则该塔的高度OP=( )
A.25米 B.25米 C.50米 D.25米
6.(2024山东菏泽外国语学校月考)如图,一辆汽车在一条水平的公路上向正西方向行驶,到A处时测得公路北侧一座山的山底C在西偏北30°的方向上,行驶600 m后到达B处,测得此山底C在西偏北75°的方向上,且山顶D的仰角为30°,则此山的高度CD= .
题组三 角度问题
7.(2022四川宜宾四中期中)如图所示,在一个坡度一定的山坡AC上有一高度为25 m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50 m到达B处,又测得∠DBC=45°,根据以上数据可得cos θ= .
8.(2022山东东营期末)如图,一条巡逻船由南向北行驶,在A处测得灯塔底部C在北偏东15°方向上,匀速向北航行20分钟到达B处,此时测得灯塔底部C在北偏东60°方向上,测得塔顶P的仰角为60°,已知灯塔高PC=2 km.
(1)求巡逻船的航行速度;
(2)若该船继续匀速向北航行10分钟到达D处,问此时灯塔底部C位于D的什么方向
9.(2022江苏盐城期中)一个以AB为直径的半圆形湖如图所示,AB=8百米,现在设计一个以AB为边的四边形ABCD,C,D在半圆上,设∠BOC=θ(O为圆心).
(1)在四边形ABCD内种植荷花,且∠COD=,当θ为何值时,荷花种植面积最大
(2)为了显示美感,景观要错落有致,为此举办方沿BC,CD和DA建造观景栈桥,且BC=CD,当θ为何值时,观景栈桥总长L最大 并求L的最大值.
能力提升练
题组 正、余弦定理的实际应用
1.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面下方,点O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.在A地测得C处的俯角为15°,最高点H的仰角为30°,则该仪器的垂直弹射高度CH为( )
A.210(+)米 B.140米
C.210米 D.210(-)米
2.(2022陕西西安长安第一中学期中)如图所示,为测量两塔塔尖M、N之间的距离,选择地面上一点C为观测点,测得∠MCN=150°,AC=60 m,BC=70 m,tan∠MCA=,cos∠NCB=,则两塔塔尖M、N之间的距离为( )
A.75 m B.150 m C.75 m D.75 m
3.2017年9月16日05时,第19号台风“杜苏芮”的中心位于甲地,它以每小时30千米的速度向西偏北θ的方向移动,距台风中心t千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受到台风影响,则t和θ的值分别为(附:≈8.585)( )
A.858.5,60° B.858.5,30°
C.717,60° D.717,30°
4.(多选题)(2024河南商丘月考)如图,为测量海岛的高度AB以及其最高处瞭望塔的塔高BC,测量船沿航线DA航行,且DA与AC在同一铅直平面内,测量船在D处测得∠BDA=α,∠CDA=β,然后沿航线DA向海岛的方向航行m千米到达E处,测得∠BEA=γ,∠CEA=δ(δ>γ>β>α,测量船的高度忽略不计),则( )
A.AB= B.AE=
C.BC= D.AC=
5.(2022安徽宿州十三所重点中学期中联考)某同学为测量教学楼AB的高度,先在地面上选择一点C,测量出∠ACB=α,再分别执行如下四种测量方案,则利用测量数据可表示出教学楼高度的方案编号为 .
方案(1):从点C向教学楼前进a米到达点D,测量出∠ADB=β;
方案(2):在地面上另选点D,测量出∠ACD=β,∠ADC=γ,CD=a米;
方案(3):在地面上另选点D,测量出∠BDC=β,CD=a米;
方案(4):从过点C的直线上(不过点B)另选点D、E,测量出CD=2DE=a米,∠ADB=β,∠AEB=γ.
6.(2024广东广州执信中学月考)如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C,现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再匀速步行到C,假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量得cos A=,sin B=.
(1)乙出发多少分钟后,乙(乙在缆车上)与甲之间的距离最短
(2)为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内
7.(2022上海松江期末)为打赢脱贫攻坚战,某村加大旅游业投入,准备将如图所示的扇形空地AOB分隔成三部分,建成花卉观赏区,分别种植玫瑰花、郁金香和菊花,已知扇形的半径为100米,圆心角为π,点P在扇形的弧上,点Q在OB上,且PQ∥OA.
(1)当Q是OB的中点时,求PQ的长;(精确到米)
(2)已知种植玫瑰花、郁金香和菊花的成本分别为30元/平方米、50元/平方米、20元/平方米,要使郁金香种植区△OPQ的面积尽可能大,求△OPQ面积的最大值,并求此时扇形区域AOB种植花卉的总成本.(精确到元)
答案与分层梯度式解析
基础过关练
1.C 由题意可知A=30°,D=45°,∠PCB=60°,
所以∠DPC=15°,∠APC=90°.
因为sin 15°=sin(45°-30°)=,
所以在△PCD中,由正弦定理得=,即=,解得PC=100(+1)m,所以在Rt△PAC中,AC=2PC=200(+1)m,
所以BC=AC-AB=200 m.故选C.
2.A 设甲驱逐舰、乙护卫舰、航母所在位置分别为A,B,C,则∠ACB=45°+15°=60°,∠BAC=90°-15°=75°,∠ABC=180°-60°-75°=45°.在△ABC中,由正弦定理得=,即=,解得AB=6,即甲驱逐舰与乙护卫舰的距离为6海里.故选A.
3.D 在△ACD中,∠ADC=30°,∠ACD=∠ACB+∠BCD=75°+45°=120°,
∴∠CAD=180°-120°-30°=30°,∴AC=CD=12 m.
在△BCD中,∠BCD=45°,∠BDC=45°+30°=75°,
∴∠CBD=180°-45°-75°=60°,
∴BC===(6+2)m.
在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠ACB=122+(6+2)2-2×12×(6+2)×cos 75°=240,∴AB=4 m.故A,B两点之间的距离为4 m.
规律总结 (1)当A,B两点不相通,又不可视时,选取直线AB外一点C,测出AC,BC,∠ACB,用余弦定理求出AB的长;
(2)当A,B两点可视,但点B不可到达时,选取直线AB外一点C,测出∠CAB,∠ACB和AC,用正弦定理求出AB的长;
(3)当A,B两点都不可达时,选取对A,B可视的点C,D(不在直线AB上),测出∠BCA,∠BDA,∠BCD,∠ADC和CD,用正弦定理和余弦定理求出AB的长.
4.B 由题意知,∠CAM=15°+45°=60°,∠AMC=180°-60°-45°=75°,所以∠ACM=45°.
在Rt△ABM中,AM=AB=36(m),
在△ACM中,由正弦定理得=,即=,
所以CM==36(m),
在Rt△DCM中,CD=CMsin 60°=54(m),
故选B.
5.B 由题意可知,∠OAP=60°,∠OBP=45°,
设OP=h米,
在Rt△AOP中,OA===h米,
在Rt△BOP中,OB===h米.
在△AOB中,由余弦定理可得AB2=OA2+OB2-2OA·OBcos∠AOB=h2+h2-2×h2×=h2,解得h=AB=25米.
故选B.
6.答案 100 m
解析 由题可得∠CAB=30°,∠CBA=180°-75°=105°,则∠BCA=45°.
在△ABC中,由正弦定理得=,则CB===300(m).
在Rt△CBD中,∠CBD=30°,
所以tan∠CBD==,则CD=CB=100(m).
解题模板 解决空间中测量高度问题时,先确定其所在平面.将空间问题转化为平面问题,利用“解直角三角形”与“解斜三角形”结合.在解题中,要综合运用立体几何知识与平面几何知识,注意方程思想的运用.
7.答案 -1
解析 由∠DAC=15°,∠DBC=45°,
可得∠DBA=135°,∠ADB=30°.
在△ABD中,由正弦定理得=,
即=,所以BD=100×sin 15°=100×sin(45°-30°)=25(-)m.
在△BCD中,由正弦定理得=,
即=,
解得sin∠BCD=-1.
所以cos θ=cos(∠BCD-90°)=sin∠BCD=-1.
8.解析 (1)在Rt△BCP中,tan∠PBC=,
即tan 60°=,所以BC=2 km.
在△ABC中,∠BCA=180°-15°-120°=45°,
由正弦定理,得=,
即=,
所以AB=2(+1)km,
又从A处到B处用时20分钟,
所以巡逻船的航行速度v==6(+1)km/h.
(2)在△BCD中,BC=2 km,BD=×6(+1)=(+1)km,∠DBC=60°,
由余弦定理可得CD2=BC2+BD2-2BC·BD·cos∠DBC=6,所以CD= km,
在△BCD中,由正弦定理得=,
即=,
解得sin∠CDB=,
又CB故此时灯塔底部C位于D处的南偏东45°,且C、D两点相距 km.
9.解析 (1)因为AB=8百米,所以OA=OB=OC=OD=4百米,
S四边形ABCD=S△BOC+S△COD+S△DOA
=OB·OCsin θ+OC·ODsin+OD·OAsin
=×42×sin θ+×42×sin+×42×sin
=8sin+4.
由已知得0<θ<,所以<θ+<,
所以当θ+=,即θ=时,荷花种植面积最大.
(2)因为BC=CD,
所以∠COD=∠BOC=θ,且0<θ<,
在△BOC与△DOA中,由余弦定理得
BC==8sin,
DA==8cos θ,
所以L=16sin+8cos θ,令t=sin,
因为0<<,所以0则L=16sin+8=-16+12,
所以当t=,即θ=时,L取得最大值12,
因此当θ=时,观景栈桥总长L最大,L的最大值为12百米.
能力提升练
1.B 由题意,设AC=x米,则BC=(x-40)米,在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC,即(x-40)2=10 000+x2-100x,解得x=420.
在△ACH中,AC=420米,∠CAH=30°+15°=45°,∠AHC=90°-30°=60°,
由正弦定理得=,
所以CH=AC·=420×=140(米).
2.C 在Rt△MAC中,可得cos∠MCA=,则CM===75(m).
在Rt△BCN中,可得CN===75(m).
在△MNC中,由余弦定理得
MN=
==75(m).
故两塔塔尖M、N之间的距离为75 m.故选C.
3.A 根据题意,3小时后台风中心距甲地90千米,27小时后台风中心距甲地810千米,乙地有24小时在台风范围内,根据余弦定理得t2=9002+902-2×900×90cos θ,t2=9002+8102-2×900×810cos θ,解得cos θ=,因为0°<θ<90°,所以θ=60°,所以t2=9002+902-2×900×90×cos 60°=737 100,所以t=858.5.
4.ACD 在△BDE中,∠BDE=α,∠DBE=∠BEA-∠BDE=γ-α,∠BED=π-γ,
由正弦定理得,==,即==,所以BD=,BE=,所以AB=BDsin α=,AE=BEcos γ=,A正确,B错误;
在△BCE中,∠BCE=-δ,∠BEC=δ-γ,由正弦定理得=,
所以BC==,C正确;
在△CDE中,∠CDE=β,∠DCE=∠CEA-∠CDE=δ-β,∠CED=π-δ,由正弦定理得=,所以CD=,
所以AC=CDsin β=,D正确.
故选ACD.
5.答案 (1)(2)(4)
解析 对于方案(1),∠CAD=∠ADB-∠ACB=β-α,在△ACD中,由正弦定理可得=,
所以AD=米,在Rt△ABD中,AB=ADsin β=米,所以方案(1)满足条件;
对于方案(2),在△ACD中,由正弦定理得=,所以AC=米,
在Rt△ABC中,AB=ACsin α=米,方案(2)满足条件;
对于方案(3),在△BCD中,已知CD=a米,∠BDC=β,无法求出BC的长,从而无法求出AB的长,方案(3)不满足条件;
对于方案(4),设AB=x米,则BC=米,BD=米,BE=米,
因为cos∠BDC=cos(π-∠BDE)=-cos∠BDE,
所以cos∠BDC+cos∠BDE=+=0,可得出关于x的方程,即可解得x的值,方案(4)满足条件.
故满足题意的方案编号为(1)(2)(4).
6.思路分析 (1)先求得sin C,然后由正弦定理求得AB,假设乙出发t min后,甲、乙两游客距离为d,利用余弦定理列解析式,结合二次函数的性质求得d的最小值.(2)根据“两位游客在C处互相等待的时间不超过3 min”列不等式,由此求得乙步行的速度的范围.
解析 (1)由cos A=,sin B=,且B为钝角、A为锐角可得,sin A=,cos B=-=-,
在△ABC中,sin C=sin(A+B)=sin Acos B+cos A·sin B=×+×=,
由正弦定理得=,即=,解得AB=1 040(m).
所以索道AB的长为1 040 m,
假设乙出发t min后(乙在缆车上),甲、乙两游客之间的距离为d m,易知0≤t≤,即0≤t≤8.
此时甲行走了(100+50t)m,乙距离A处130t m,
由余弦定理得d2=(100+50t)2+(130t)2-2×(100+50t)×130t×=200(37t2-70t+50),0≤t≤8.
易得函数y=37t2-70t+50的图象的对称轴方程为t=,且图象开口向上,
所以当t=时,d有最小值,即乙出发 min后,甲、乙两游客之间的距离最短.
(2)在△ABC中,由正弦定理得=,
解得BC=sin A×=×=500(m),
乙从B出发时,甲已经走了50×(2+8+1)=550 m,还需要走1 260-550=710 m才能到达C处,
设乙步行的速度为v m/min(v>0),
由题意得-3≤-≤3,解得≤v≤,
所以为了使两位游客在C处互相等待的时间不超过3 min,乙步行的速度(单位:m/min)应控制在内.
7.解析 由题意知,扇形的半径为100米=1百米.
(1)当Q是OB的中点时,OQ=百米,∠PQO=,OP=1百米,
在△OPQ中,由余弦定理可得OP2=OQ2+PQ2-2OQ·PQ·cos,
所以PQ=≈1.15,
所以当Q是OB的中点时,PQ的长约为115米.
(2)设∠AOP=x,则x∈,
在△OPQ中,由正弦定理知
==,
所以PQ=sin,
所以△OPQ的面积S1=PQ·OP·sin x
=sinsin x=sin x×
=sin xcos x+sin2x=sin 2x+×(1-cos 2x)
=sin 2x-cos 2x+
=平方百米,
因为0所以当2x-=,即x=时,△OPQ的面积最大,为平方百米,即2 500平方米,
当x=时,PQ=OP=1百米,故扇形AOP的面积S2=××12=平方百米,即平方米,
扇形AOB的面积S=××12=平方百米,即平方米,
所以区域BQP的面积S3=S-S1-S2
=-2 500-
=平方米,
因为种植玫瑰花、郁金香和菊花的成本分别为30元/平方米、50元/平方米、20元/平方米,
所以此时扇形区域AOB种植花卉的总成本为30×+50×2 500+20×=+75 000≈391 703(元).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第四册
第九章 解三角形
9.2 正弦定理与余弦定理的应用
9.3 数学探究活动:得到不可达两点之间的距离
基础过关练
题组一 距离问题
1.如图,已知A,B,C,D四点在同一条直线上,且平面PAD与地面垂直,在山顶P测得点A,C,D的俯角分别为30°,60°,45°,并测得AB=200 m,CD=100 m,现欲沿直线AD开通穿山隧道,则隧道BC的长为( )
A.100(+1)m B.200(+1)m
C.200 m D.100 m
2.(2022陕西渭南期末)在某次海军演习中,已知甲驱逐舰在航母的南偏东15°方向且与航母的距离为12海里,乙护卫舰在甲驱逐舰的正西方向,若测得乙护卫舰在航母的南偏西45°方向,则甲驱逐舰与乙护卫舰之间的距离为( )
A.6海里 B.6海里
C.4海里 D.12海里
3.如图,要测量河对岸A,B两点间的距离,现沿河岸选取相距12 m的C,D两点,测得∠ACB=75°,∠BCD=45°,∠ADB=45°,∠ADC=30°,则A,B两点之间的距离是( )
A.4 m B.4 m C.4 m D.4 m
题组二 高度问题
4.(2024福建三明第一中学月考)2023年入冬以来,哈尔滨冰雪旅游火爆出圈.圣·索菲亚教堂是哈尔滨的标志性建筑,其中央主体建筑集球、圆柱、棱柱于一体,极具对称之美.为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物AB,高约为36 m,在它们之间的地面上的点M(B,M,D三点共线)处测得楼顶A、教堂顶C的仰角分别是45°和60°,在楼顶A处测得教堂顶C的仰角为15°,则索菲亚教堂的高度CD约为( )
A.50 m B.54 m C.58 m D.60 m
5.(2024浙江杭州富阳场口中学教学质量检测)桂林日月塔又称金塔银塔、情侣塔,日塔别名叫金塔,月塔别名叫银塔,所以也有金银塔之称.如图1,这是金银塔中的金塔,某数学兴趣小组成员为测量该塔的高度,在塔底O的同一水平面上的A,B两点处进行测量,如图2.已知在A处测得塔顶P的仰角为60°,在B处测得塔顶P的仰角为45°,AB=25米,∠AOB=30°,则该塔的高度OP=( )
A.25米 B.25米 C.50米 D.25米
6.(2024山东菏泽外国语学校月考)如图,一辆汽车在一条水平的公路上向正西方向行驶,到A处时测得公路北侧一座山的山底C在西偏北30°的方向上,行驶600 m后到达B处,测得此山底C在西偏北75°的方向上,且山顶D的仰角为30°,则此山的高度CD= .
题组三 角度问题
7.(2022四川宜宾四中期中)如图所示,在一个坡度一定的山坡AC上有一高度为25 m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50 m到达B处,又测得∠DBC=45°,根据以上数据可得cos θ= .
8.(2022山东东营期末)如图,一条巡逻船由南向北行驶,在A处测得灯塔底部C在北偏东15°方向上,匀速向北航行20分钟到达B处,此时测得灯塔底部C在北偏东60°方向上,测得塔顶P的仰角为60°,已知灯塔高PC=2 km.
(1)求巡逻船的航行速度;
(2)若该船继续匀速向北航行10分钟到达D处,问此时灯塔底部C位于D的什么方向
9.(2022江苏盐城期中)一个以AB为直径的半圆形湖如图所示,AB=8百米,现在设计一个以AB为边的四边形ABCD,C,D在半圆上,设∠BOC=θ(O为圆心).
(1)在四边形ABCD内种植荷花,且∠COD=,当θ为何值时,荷花种植面积最大
(2)为了显示美感,景观要错落有致,为此举办方沿BC,CD和DA建造观景栈桥,且BC=CD,当θ为何值时,观景栈桥总长L最大 并求L的最大值.
能力提升练
题组 正、余弦定理的实际应用
1.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面下方,点O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点A,B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.在A地测得C处的俯角为15°,最高点H的仰角为30°,则该仪器的垂直弹射高度CH为( )
A.210(+)米 B.140米
C.210米 D.210(-)米
2.(2022陕西西安长安第一中学期中)如图所示,为测量两塔塔尖M、N之间的距离,选择地面上一点C为观测点,测得∠MCN=150°,AC=60 m,BC=70 m,tan∠MCA=,cos∠NCB=,则两塔塔尖M、N之间的距离为( )
A.75 m B.150 m C.75 m D.75 m
3.2017年9月16日05时,第19号台风“杜苏芮”的中心位于甲地,它以每小时30千米的速度向西偏北θ的方向移动,距台风中心t千米以内的地区都将受到影响,若16日08时到17日08时,距甲地正西方向900千米的乙地恰好受到台风影响,则t和θ的值分别为(附:≈8.585)( )
A.858.5,60° B.858.5,30°
C.717,60° D.717,30°
4.(多选题)(2024河南商丘月考)如图,为测量海岛的高度AB以及其最高处瞭望塔的塔高BC,测量船沿航线DA航行,且DA与AC在同一铅直平面内,测量船在D处测得∠BDA=α,∠CDA=β,然后沿航线DA向海岛的方向航行m千米到达E处,测得∠BEA=γ,∠CEA=δ(δ>γ>β>α,测量船的高度忽略不计),则( )
A.AB= B.AE=
C.BC= D.AC=
5.(2022安徽宿州十三所重点中学期中联考)某同学为测量教学楼AB的高度,先在地面上选择一点C,测量出∠ACB=α,再分别执行如下四种测量方案,则利用测量数据可表示出教学楼高度的方案编号为 .
方案(1):从点C向教学楼前进a米到达点D,测量出∠ADB=β;
方案(2):在地面上另选点D,测量出∠ACD=β,∠ADC=γ,CD=a米;
方案(3):在地面上另选点D,测量出∠BDC=β,CD=a米;
方案(4):从过点C的直线上(不过点B)另选点D、E,测量出CD=2DE=a米,∠ADB=β,∠AEB=γ.
6.(2024广东广州执信中学月考)如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C,现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再匀速步行到C,假设缆车匀速直线运动的速度为130 m/min,山路AC长为1 260 m,经测量得cos A=,sin B=.
(1)乙出发多少分钟后,乙(乙在缆车上)与甲之间的距离最短
(2)为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内
7.(2022上海松江期末)为打赢脱贫攻坚战,某村加大旅游业投入,准备将如图所示的扇形空地AOB分隔成三部分,建成花卉观赏区,分别种植玫瑰花、郁金香和菊花,已知扇形的半径为100米,圆心角为π,点P在扇形的弧上,点Q在OB上,且PQ∥OA.
(1)当Q是OB的中点时,求PQ的长;(精确到米)
(2)已知种植玫瑰花、郁金香和菊花的成本分别为30元/平方米、50元/平方米、20元/平方米,要使郁金香种植区△OPQ的面积尽可能大,求△OPQ面积的最大值,并求此时扇形区域AOB种植花卉的总成本.(精确到元)
答案与分层梯度式解析
基础过关练
1.C 由题意可知A=30°,D=45°,∠PCB=60°,
所以∠DPC=15°,∠APC=90°.
因为sin 15°=sin(45°-30°)=,
所以在△PCD中,由正弦定理得=,即=,解得PC=100(+1)m,所以在Rt△PAC中,AC=2PC=200(+1)m,
所以BC=AC-AB=200 m.故选C.
2.A 设甲驱逐舰、乙护卫舰、航母所在位置分别为A,B,C,则∠ACB=45°+15°=60°,∠BAC=90°-15°=75°,∠ABC=180°-60°-75°=45°.在△ABC中,由正弦定理得=,即=,解得AB=6,即甲驱逐舰与乙护卫舰的距离为6海里.故选A.
3.D 在△ACD中,∠ADC=30°,∠ACD=∠ACB+∠BCD=75°+45°=120°,
∴∠CAD=180°-120°-30°=30°,∴AC=CD=12 m.
在△BCD中,∠BCD=45°,∠BDC=45°+30°=75°,
∴∠CBD=180°-45°-75°=60°,
∴BC===(6+2)m.
在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠ACB=122+(6+2)2-2×12×(6+2)×cos 75°=240,∴AB=4 m.故A,B两点之间的距离为4 m.
规律总结 (1)当A,B两点不相通,又不可视时,选取直线AB外一点C,测出AC,BC,∠ACB,用余弦定理求出AB的长;
(2)当A,B两点可视,但点B不可到达时,选取直线AB外一点C,测出∠CAB,∠ACB和AC,用正弦定理求出AB的长;
(3)当A,B两点都不可达时,选取对A,B可视的点C,D(不在直线AB上),测出∠BCA,∠BDA,∠BCD,∠ADC和CD,用正弦定理和余弦定理求出AB的长.
4.B 由题意知,∠CAM=15°+45°=60°,∠AMC=180°-60°-45°=75°,所以∠ACM=45°.
在Rt△ABM中,AM=AB=36(m),
在△ACM中,由正弦定理得=,即=,
所以CM==36(m),
在Rt△DCM中,CD=CMsin 60°=54(m),
故选B.
5.B 由题意可知,∠OAP=60°,∠OBP=45°,
设OP=h米,
在Rt△AOP中,OA===h米,
在Rt△BOP中,OB===h米.
在△AOB中,由余弦定理可得AB2=OA2+OB2-2OA·OBcos∠AOB=h2+h2-2×h2×=h2,解得h=AB=25米.
故选B.
6.答案 100 m
解析 由题可得∠CAB=30°,∠CBA=180°-75°=105°,则∠BCA=45°.
在△ABC中,由正弦定理得=,则CB===300(m).
在Rt△CBD中,∠CBD=30°,
所以tan∠CBD==,则CD=CB=100(m).
解题模板 解决空间中测量高度问题时,先确定其所在平面.将空间问题转化为平面问题,利用“解直角三角形”与“解斜三角形”结合.在解题中,要综合运用立体几何知识与平面几何知识,注意方程思想的运用.
7.答案 -1
解析 由∠DAC=15°,∠DBC=45°,
可得∠DBA=135°,∠ADB=30°.
在△ABD中,由正弦定理得=,
即=,所以BD=100×sin 15°=100×sin(45°-30°)=25(-)m.
在△BCD中,由正弦定理得=,
即=,
解得sin∠BCD=-1.
所以cos θ=cos(∠BCD-90°)=sin∠BCD=-1.
8.解析 (1)在Rt△BCP中,tan∠PBC=,
即tan 60°=,所以BC=2 km.
在△ABC中,∠BCA=180°-15°-120°=45°,
由正弦定理,得=,
即=,
所以AB=2(+1)km,
又从A处到B处用时20分钟,
所以巡逻船的航行速度v==6(+1)km/h.
(2)在△BCD中,BC=2 km,BD=×6(+1)=(+1)km,∠DBC=60°,
由余弦定理可得CD2=BC2+BD2-2BC·BD·cos∠DBC=6,所以CD= km,
在△BCD中,由正弦定理得=,
即=,
解得sin∠CDB=,
又CB
9.解析 (1)因为AB=8百米,所以OA=OB=OC=OD=4百米,
S四边形ABCD=S△BOC+S△COD+S△DOA
=OB·OCsin θ+OC·ODsin+OD·OAsin
=×42×sin θ+×42×sin+×42×sin
=8sin+4.
由已知得0<θ<,所以<θ+<,
所以当θ+=,即θ=时,荷花种植面积最大.
(2)因为BC=CD,
所以∠COD=∠BOC=θ,且0<θ<,
在△BOC与△DOA中,由余弦定理得
BC==8sin,
DA==8cos θ,
所以L=16sin+8cos θ,令t=sin,
因为0<<,所以0
所以当t=,即θ=时,L取得最大值12,
因此当θ=时,观景栈桥总长L最大,L的最大值为12百米.
能力提升练
1.B 由题意,设AC=x米,则BC=(x-40)米,在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC,即(x-40)2=10 000+x2-100x,解得x=420.
在△ACH中,AC=420米,∠CAH=30°+15°=45°,∠AHC=90°-30°=60°,
由正弦定理得=,
所以CH=AC·=420×=140(米).
2.C 在Rt△MAC中,可得cos∠MCA=,则CM===75(m).
在Rt△BCN中,可得CN===75(m).
在△MNC中,由余弦定理得
MN=
==75(m).
故两塔塔尖M、N之间的距离为75 m.故选C.
3.A 根据题意,3小时后台风中心距甲地90千米,27小时后台风中心距甲地810千米,乙地有24小时在台风范围内,根据余弦定理得t2=9002+902-2×900×90cos θ,t2=9002+8102-2×900×810cos θ,解得cos θ=,因为0°<θ<90°,所以θ=60°,所以t2=9002+902-2×900×90×cos 60°=737 100,所以t=858.5.
4.ACD 在△BDE中,∠BDE=α,∠DBE=∠BEA-∠BDE=γ-α,∠BED=π-γ,
由正弦定理得,==,即==,所以BD=,BE=,所以AB=BDsin α=,AE=BEcos γ=,A正确,B错误;
在△BCE中,∠BCE=-δ,∠BEC=δ-γ,由正弦定理得=,
所以BC==,C正确;
在△CDE中,∠CDE=β,∠DCE=∠CEA-∠CDE=δ-β,∠CED=π-δ,由正弦定理得=,所以CD=,
所以AC=CDsin β=,D正确.
故选ACD.
5.答案 (1)(2)(4)
解析 对于方案(1),∠CAD=∠ADB-∠ACB=β-α,在△ACD中,由正弦定理可得=,
所以AD=米,在Rt△ABD中,AB=ADsin β=米,所以方案(1)满足条件;
对于方案(2),在△ACD中,由正弦定理得=,所以AC=米,
在Rt△ABC中,AB=ACsin α=米,方案(2)满足条件;
对于方案(3),在△BCD中,已知CD=a米,∠BDC=β,无法求出BC的长,从而无法求出AB的长,方案(3)不满足条件;
对于方案(4),设AB=x米,则BC=米,BD=米,BE=米,
因为cos∠BDC=cos(π-∠BDE)=-cos∠BDE,
所以cos∠BDC+cos∠BDE=+=0,可得出关于x的方程,即可解得x的值,方案(4)满足条件.
故满足题意的方案编号为(1)(2)(4).
6.思路分析 (1)先求得sin C,然后由正弦定理求得AB,假设乙出发t min后,甲、乙两游客距离为d,利用余弦定理列解析式,结合二次函数的性质求得d的最小值.(2)根据“两位游客在C处互相等待的时间不超过3 min”列不等式,由此求得乙步行的速度的范围.
解析 (1)由cos A=,sin B=,且B为钝角、A为锐角可得,sin A=,cos B=-=-,
在△ABC中,sin C=sin(A+B)=sin Acos B+cos A·sin B=×+×=,
由正弦定理得=,即=,解得AB=1 040(m).
所以索道AB的长为1 040 m,
假设乙出发t min后(乙在缆车上),甲、乙两游客之间的距离为d m,易知0≤t≤,即0≤t≤8.
此时甲行走了(100+50t)m,乙距离A处130t m,
由余弦定理得d2=(100+50t)2+(130t)2-2×(100+50t)×130t×=200(37t2-70t+50),0≤t≤8.
易得函数y=37t2-70t+50的图象的对称轴方程为t=,且图象开口向上,
所以当t=时,d有最小值,即乙出发 min后,甲、乙两游客之间的距离最短.
(2)在△ABC中,由正弦定理得=,
解得BC=sin A×=×=500(m),
乙从B出发时,甲已经走了50×(2+8+1)=550 m,还需要走1 260-550=710 m才能到达C处,
设乙步行的速度为v m/min(v>0),
由题意得-3≤-≤3,解得≤v≤,
所以为了使两位游客在C处互相等待的时间不超过3 min,乙步行的速度(单位:m/min)应控制在内.
7.解析 由题意知,扇形的半径为100米=1百米.
(1)当Q是OB的中点时,OQ=百米,∠PQO=,OP=1百米,
在△OPQ中,由余弦定理可得OP2=OQ2+PQ2-2OQ·PQ·cos,
所以PQ=≈1.15,
所以当Q是OB的中点时,PQ的长约为115米.
(2)设∠AOP=x,则x∈,
在△OPQ中,由正弦定理知
==,
所以PQ=sin,
所以△OPQ的面积S1=PQ·OP·sin x
=sinsin x=sin x×
=sin xcos x+sin2x=sin 2x+×(1-cos 2x)
=sin 2x-cos 2x+
=平方百米,
因为0
当x=时,PQ=OP=1百米,故扇形AOP的面积S2=××12=平方百米,即平方米,
扇形AOB的面积S=××12=平方百米,即平方米,
所以区域BQP的面积S3=S-S1-S2
=-2 500-
=平方米,
因为种植玫瑰花、郁金香和菊花的成本分别为30元/平方米、50元/平方米、20元/平方米,
所以此时扇形区域AOB种植花卉的总成本为30×+50×2 500+20×=+75 000≈391 703(元).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
