2025人教B版高中数学必修第四册强化练习题(含解析)--11.1.3 多面体与棱柱
文档属性
| 名称 | 2025人教B版高中数学必修第四册强化练习题(含解析)--11.1.3 多面体与棱柱 |

|
|
| 格式 | docx | ||
| 文件大小 | 516.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 11:06:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第四册
第十一章 立体几何初步
11.1 空间几何体
11.1.3 多面体与棱柱
基础过关练
题组一 多面体与棱柱
1.(2022广东阳江月考)如图,长方体ABCD-A1B1C1D1被平面分成三部分,其中EF∥GH∥BC,则这三个几何体中是棱柱的个数为( )
A.0 B.1 C.2 D.3
2.(2023天津耀华中学期中)在斜四棱柱的侧面中,矩形最多有( )
A.1个 B.2个 C.3个 D.4个
3.(2023山东潍坊临朐实验中学月考)下列说法错误的是( )
A.正方体一定是正四棱柱
B.底面是正多边形的棱柱是正棱柱
C.所有侧面均是矩形的棱柱是直棱柱
D.平行六面体的六个面均为平行四边形
4.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的体对角线,那么一个五棱柱的体对角线的条数为( )
A.20 B.15 C.12 D.10
5.(2024上海风华中学期中)如果一个多面体的所有面都是全等的正三角形或正多边形,且每个顶点聚集的棱的条数都相等,那么这个多面体就叫做正多面体.下列几何体中,所有棱长均相等,同一表面的角都相等,则 是正多面体.(写出所有正确的序号)
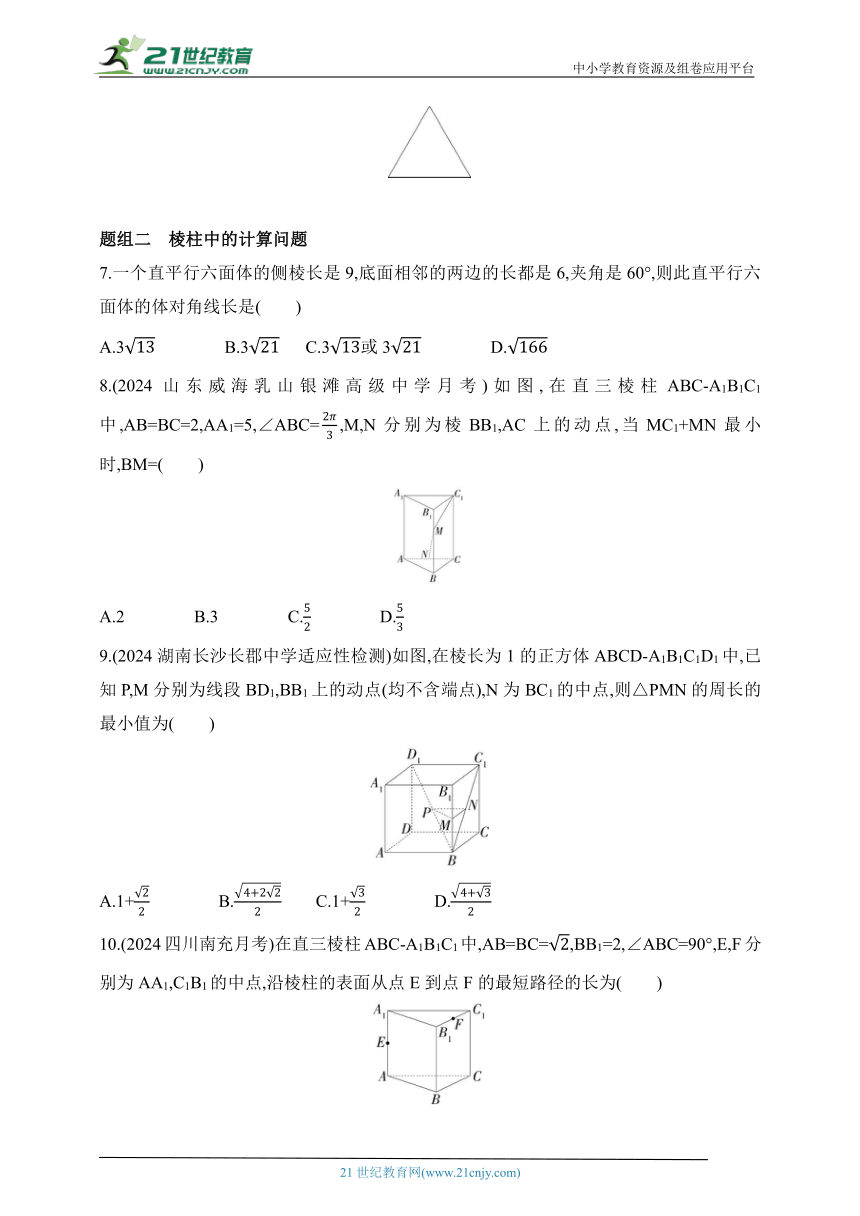
6.给出一块正三角形纸片(如图所示),要求将其剪拼成一个底面为正三角形的三棱柱模型,请设计一种剪接方案,用虚线标示在图中,并作简要说明.
题组二 棱柱中的计算问题
7.一个直平行六面体的侧棱长是9,底面相邻的两边的长都是6,夹角是60°,则此直平行六面体的体对角线长是( )
A.3 B.3 C.3或3 D.
8.(2024山东威海乳山银滩高级中学月考)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AA1=5,∠ABC=,M,N分别为棱BB1,AC上的动点,当MC1+MN最小时,BM=( )
A.2 B.3 C. D.
9.(2024湖南长沙长郡中学适应性检测)如图,在棱长为1的正方体ABCD-A1B1C1D1中,已知P,M分别为线段BD1,BB1上的动点(均不含端点),N为BC1的中点,则△PMN的周长的最小值为( )
A.1+ B. C.1+ D.
10.(2024四川南充月考)在直三棱柱ABC-A1B1C1中,AB=BC=,BB1=2,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从点E到点F的最短路径的长为( )
A. B. C. D.+
11.正六棱柱的一条最长的体对角线长是13,侧面积为180,求此正六棱柱的表面积.
题组三 多面体的截面问题
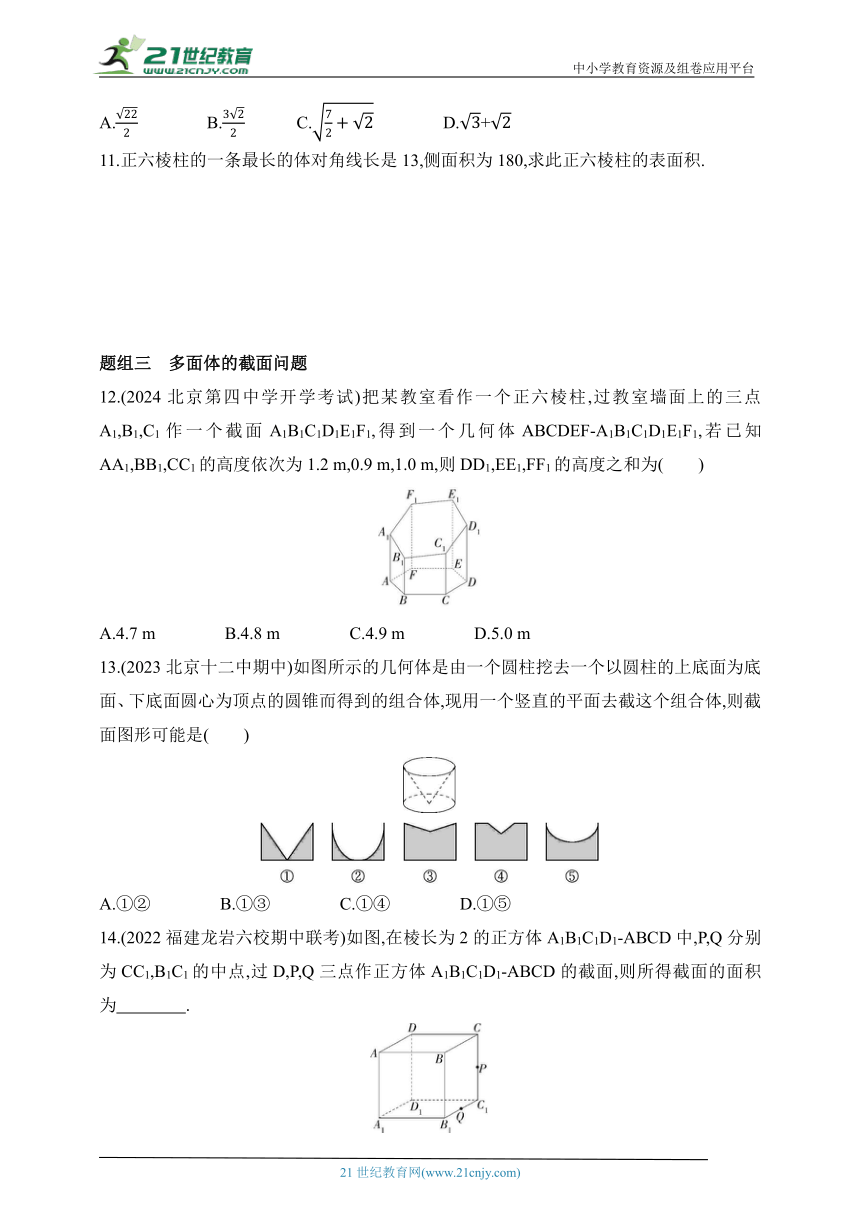
12.(2024北京第四中学开学考试)把某教室看作一个正六棱柱,过教室墙面上的三点A1,B1,C1作一个截面A1B1C1D1E1F1,得到一个几何体ABCDEF-A1B1C1D1E1F1,若已知AA1,BB1,CC1的高度依次为1.2 m,0.9 m,1.0 m,则DD1,EE1,FF1的高度之和为( )
A.4.7 m B.4.8 m C.4.9 m D.5.0 m
13.(2023北京十二中期中)如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面、下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①② B.①③ C.①④ D.①⑤
14.(2022福建龙岩六校期中联考)如图,在棱长为2的正方体A1B1C1D1-ABCD中,P,Q分别为CC1,B1C1的中点,过D,P,Q三点作正方体A1B1C1D1-ABCD的截面,则所得截面的面积为 .
答案与分层梯度式解析
基础过关练
1.D 2.B
3.B 对于A,上、下底面都是正方形,且侧棱垂直于底面的棱柱是正四棱柱,所以正方体是正四棱柱,故A中的说法正确;
对于B,底面是正多边形的直棱柱是正棱柱,故B中的说法错误;
对于C,由直棱柱的定义知C中的说法正确;
对于D,底面是平行四边形的棱柱称为平行六面体,而棱柱的各个侧面都是平行四边形,故D中的说法正确.
4.D 如图,在五棱柱ABCDE-A1B1C1D1E1中,从顶点A出发的体对角线有2条:AC1,AD1,同理,从顶点B,C,D,E出发的体对角线均有2条,共2×5=10(条).
5.答案 (1)(2)(4)
解析 对于(1),该多面体由全等的正三角形组成,且每个顶点聚集的棱有3条,符合题意;
对于(2),该多面体由全等的正四边形组成,且每个顶点聚集的棱有3条,符合题意;
对于(3),该多面体由全等的正三角形组成,每个顶点聚集的棱有3条或4条,不符合题意;
对于(4),该多面体由全等的正五边形组成,且每个顶点聚集的棱有3条,符合题意.
故正多面体有(1)(2)(4).
6.解析 取△ABC的内心O,连接OA,OB,OC,再分别取OA,OB,OC的中点D,E,F,连成小三角形DEF,过点D作AB,AC的垂线,过点E作AB,BC的垂线,过点F作BC,AC的垂线,最后分别在点D,E,F处沿虚线剪三刀,剪出6个全等的直角三角形,两两拼出正三棱柱的上底面即可.
7.C 直平行六面体的体对角线有4条,共2对,分别相等,底面菱形的对角线长分别是6和6,由勾股定理可得此直平行六面体的体对角线长是=3或=3.
8.D 如图所示,过点N作NN1∥AA1,交A1C1于点N1,分别连接B1N1,BN,
将平面BCC1B1绕着BB1所在直线旋转到与平面BNN1B1共面的位置,得到矩形DNN1D1,
连接D1N,交BB1于点M1,
当D1N⊥AC时,D1到直线AC的距离最短,即MC1+MN取得最小值,
因为AB=BC=2,且∠ABC=,所以BN=1,
易知△NBM1∽△NDD1,可得=,即=,所以BM1=,
即当MC1+MN 最小时,BM=.故选D.
9.思路分析 通过证明△BOP≌△BNP,从而得到PO=PN,再将平面BDD1B1与平面BCC1B1展开至两个平面共面,在平面图形中连接ON,交BB1于点M,交D1B于点P,此时ON的长即为△PMN的周长的最小值,利用余弦定理计算即可.
B 如图1,连接BD,AC,设其交点为O,连接PO,B1D1,B1C,易知N为B1C和BC1的交点,
易知OB=NB,∠DBD1=∠C1BD1,
所以△BOP≌△BNP,所以PO=PN,把平面BDD1B1与平面BCC1B1展开至两个平面共面,如图2,
在平面图形中连接ON,交BB1于点M,交D1B于点P,此时ON的长即为△PMN的周长的最小值,
在△BON中,易得OB=BN=,由余弦定理可得ON=
=,
所以△PMN的周长的最小值为.故选B.
10.B 由题意得直三棱柱底面为等腰直角三角形.
①把平面ABB1A1和平面BCC1B1展开到同一个平面内,连接EF,
由勾股定理得EF==
=;
②把平面ACC1A1和平面BCC1B1展开到同一个平面内,连接EF,
此时EF===;
③把平面ABB1A1和平面A1B1C1展开到同一个平面内,设BB1的中点为G,连接EG,EF,
在直角三角形EGF中,由勾股定理得EF===;
④把平面ACC1A1和平面A1B1C1展开到同一个平面内,
过F作与CC1平行的直线,过E作与AC平行的直线,设这两条直线交于点H,连接EF,
由勾股定理得EF===.
由>>>,
可得从点E到点F的最短路径的长为,故选B.
名师点睛 解答本题的关键是将棱柱侧面以各种方式展开,使得E,F在同一个平面内,将立体问题转化为平面问题解决.
11.解析 如图,设正六棱柱的底面边长为a,侧棱长(即正六棱柱的高)为h,易知CF'是正六棱柱的一条最长的体对角线,即CF'=13,
易知CF=2a,FF'=h,
所以CF'===13.①
因为正六棱柱的侧面积为180,
所以S侧=6ah=180.②
联立①②,解得或
当a=6,h=5时,S上+S下=2×6×a2=108,
所以S表=180+108;
当a=,h=12时,S上+S下=2×6×a2=,
所以S表=180+.
故此正六棱柱的表面积为180+108或180+.
12.A 在正六边形ABCDEF中,连接AD,BE,CF,交于点O,易知O为正六边形ABCDEF的中心,四边形ABCO是菱形,连接AC,交BO于点H.
在六边形A1B1C1D1E1F1中,连接A1D1,B1E1,C1F1,设交点为O1,易知O1为六边形A1B1C1D1E1F1的中心,四边形A1B1C1O1为平行四边形.
连接A1C1,与B1O1交于点H1,连接HH1,OO1,易知OO1⊥平面ABCDEF,且OO1∥HH1.
由题意以及梯形的中位线性质可得AA1+CC1=2HH1=BB1+OO1,解得OO1=1.3(m),
又BE的中点为O,所以EE1+BB1=2OO1,所以EE1=1.7(m),
同理AA1+DD1=2OO1,解得DD1=1.4(m),
CC1+FF1=2OO1,解得FF1=1.6(m),
所以DD1+EE1+FF1=1.4+1.7+1.6=4.7(m).
故选A.
名师点睛 关键是利用中位线定理列方程求解.
13.D 当截面过底面直径时,截面如题图①;当截面不过底面直径时,截面如题图⑤.
14.答案
解析 如图所示,连接DA1,A1Q,PQ,DP,易知截面为四边形A1DPQ,四边形A1DPQ为等腰梯形,因为正方体A1B1C1D1-ABCD的棱长为2,且P,Q均为所在棱的中点,所以PQ==,DA1==2,PD=A1Q==,所以梯形A1DPQ的高h==,故截面的面积S=×(+2)×=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第四册
第十一章 立体几何初步
11.1 空间几何体
11.1.3 多面体与棱柱
基础过关练
题组一 多面体与棱柱
1.(2022广东阳江月考)如图,长方体ABCD-A1B1C1D1被平面分成三部分,其中EF∥GH∥BC,则这三个几何体中是棱柱的个数为( )
A.0 B.1 C.2 D.3
2.(2023天津耀华中学期中)在斜四棱柱的侧面中,矩形最多有( )
A.1个 B.2个 C.3个 D.4个
3.(2023山东潍坊临朐实验中学月考)下列说法错误的是( )
A.正方体一定是正四棱柱
B.底面是正多边形的棱柱是正棱柱
C.所有侧面均是矩形的棱柱是直棱柱
D.平行六面体的六个面均为平行四边形
4.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的体对角线,那么一个五棱柱的体对角线的条数为( )
A.20 B.15 C.12 D.10
5.(2024上海风华中学期中)如果一个多面体的所有面都是全等的正三角形或正多边形,且每个顶点聚集的棱的条数都相等,那么这个多面体就叫做正多面体.下列几何体中,所有棱长均相等,同一表面的角都相等,则 是正多面体.(写出所有正确的序号)
6.给出一块正三角形纸片(如图所示),要求将其剪拼成一个底面为正三角形的三棱柱模型,请设计一种剪接方案,用虚线标示在图中,并作简要说明.
题组二 棱柱中的计算问题
7.一个直平行六面体的侧棱长是9,底面相邻的两边的长都是6,夹角是60°,则此直平行六面体的体对角线长是( )
A.3 B.3 C.3或3 D.
8.(2024山东威海乳山银滩高级中学月考)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AA1=5,∠ABC=,M,N分别为棱BB1,AC上的动点,当MC1+MN最小时,BM=( )
A.2 B.3 C. D.
9.(2024湖南长沙长郡中学适应性检测)如图,在棱长为1的正方体ABCD-A1B1C1D1中,已知P,M分别为线段BD1,BB1上的动点(均不含端点),N为BC1的中点,则△PMN的周长的最小值为( )
A.1+ B. C.1+ D.
10.(2024四川南充月考)在直三棱柱ABC-A1B1C1中,AB=BC=,BB1=2,∠ABC=90°,E,F分别为AA1,C1B1的中点,沿棱柱的表面从点E到点F的最短路径的长为( )
A. B. C. D.+
11.正六棱柱的一条最长的体对角线长是13,侧面积为180,求此正六棱柱的表面积.
题组三 多面体的截面问题
12.(2024北京第四中学开学考试)把某教室看作一个正六棱柱,过教室墙面上的三点A1,B1,C1作一个截面A1B1C1D1E1F1,得到一个几何体ABCDEF-A1B1C1D1E1F1,若已知AA1,BB1,CC1的高度依次为1.2 m,0.9 m,1.0 m,则DD1,EE1,FF1的高度之和为( )
A.4.7 m B.4.8 m C.4.9 m D.5.0 m
13.(2023北京十二中期中)如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面、下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①② B.①③ C.①④ D.①⑤
14.(2022福建龙岩六校期中联考)如图,在棱长为2的正方体A1B1C1D1-ABCD中,P,Q分别为CC1,B1C1的中点,过D,P,Q三点作正方体A1B1C1D1-ABCD的截面,则所得截面的面积为 .
答案与分层梯度式解析
基础过关练
1.D 2.B
3.B 对于A,上、下底面都是正方形,且侧棱垂直于底面的棱柱是正四棱柱,所以正方体是正四棱柱,故A中的说法正确;
对于B,底面是正多边形的直棱柱是正棱柱,故B中的说法错误;
对于C,由直棱柱的定义知C中的说法正确;
对于D,底面是平行四边形的棱柱称为平行六面体,而棱柱的各个侧面都是平行四边形,故D中的说法正确.
4.D 如图,在五棱柱ABCDE-A1B1C1D1E1中,从顶点A出发的体对角线有2条:AC1,AD1,同理,从顶点B,C,D,E出发的体对角线均有2条,共2×5=10(条).
5.答案 (1)(2)(4)
解析 对于(1),该多面体由全等的正三角形组成,且每个顶点聚集的棱有3条,符合题意;
对于(2),该多面体由全等的正四边形组成,且每个顶点聚集的棱有3条,符合题意;
对于(3),该多面体由全等的正三角形组成,每个顶点聚集的棱有3条或4条,不符合题意;
对于(4),该多面体由全等的正五边形组成,且每个顶点聚集的棱有3条,符合题意.
故正多面体有(1)(2)(4).
6.解析 取△ABC的内心O,连接OA,OB,OC,再分别取OA,OB,OC的中点D,E,F,连成小三角形DEF,过点D作AB,AC的垂线,过点E作AB,BC的垂线,过点F作BC,AC的垂线,最后分别在点D,E,F处沿虚线剪三刀,剪出6个全等的直角三角形,两两拼出正三棱柱的上底面即可.
7.C 直平行六面体的体对角线有4条,共2对,分别相等,底面菱形的对角线长分别是6和6,由勾股定理可得此直平行六面体的体对角线长是=3或=3.
8.D 如图所示,过点N作NN1∥AA1,交A1C1于点N1,分别连接B1N1,BN,
将平面BCC1B1绕着BB1所在直线旋转到与平面BNN1B1共面的位置,得到矩形DNN1D1,
连接D1N,交BB1于点M1,
当D1N⊥AC时,D1到直线AC的距离最短,即MC1+MN取得最小值,
因为AB=BC=2,且∠ABC=,所以BN=1,
易知△NBM1∽△NDD1,可得=,即=,所以BM1=,
即当MC1+MN 最小时,BM=.故选D.
9.思路分析 通过证明△BOP≌△BNP,从而得到PO=PN,再将平面BDD1B1与平面BCC1B1展开至两个平面共面,在平面图形中连接ON,交BB1于点M,交D1B于点P,此时ON的长即为△PMN的周长的最小值,利用余弦定理计算即可.
B 如图1,连接BD,AC,设其交点为O,连接PO,B1D1,B1C,易知N为B1C和BC1的交点,
易知OB=NB,∠DBD1=∠C1BD1,
所以△BOP≌△BNP,所以PO=PN,把平面BDD1B1与平面BCC1B1展开至两个平面共面,如图2,
在平面图形中连接ON,交BB1于点M,交D1B于点P,此时ON的长即为△PMN的周长的最小值,
在△BON中,易得OB=BN=,由余弦定理可得ON=
=,
所以△PMN的周长的最小值为.故选B.
10.B 由题意得直三棱柱底面为等腰直角三角形.
①把平面ABB1A1和平面BCC1B1展开到同一个平面内,连接EF,
由勾股定理得EF==
=;
②把平面ACC1A1和平面BCC1B1展开到同一个平面内,连接EF,
此时EF===;
③把平面ABB1A1和平面A1B1C1展开到同一个平面内,设BB1的中点为G,连接EG,EF,
在直角三角形EGF中,由勾股定理得EF===;
④把平面ACC1A1和平面A1B1C1展开到同一个平面内,
过F作与CC1平行的直线,过E作与AC平行的直线,设这两条直线交于点H,连接EF,
由勾股定理得EF===.
由>>>,
可得从点E到点F的最短路径的长为,故选B.
名师点睛 解答本题的关键是将棱柱侧面以各种方式展开,使得E,F在同一个平面内,将立体问题转化为平面问题解决.
11.解析 如图,设正六棱柱的底面边长为a,侧棱长(即正六棱柱的高)为h,易知CF'是正六棱柱的一条最长的体对角线,即CF'=13,
易知CF=2a,FF'=h,
所以CF'===13.①
因为正六棱柱的侧面积为180,
所以S侧=6ah=180.②
联立①②,解得或
当a=6,h=5时,S上+S下=2×6×a2=108,
所以S表=180+108;
当a=,h=12时,S上+S下=2×6×a2=,
所以S表=180+.
故此正六棱柱的表面积为180+108或180+.
12.A 在正六边形ABCDEF中,连接AD,BE,CF,交于点O,易知O为正六边形ABCDEF的中心,四边形ABCO是菱形,连接AC,交BO于点H.
在六边形A1B1C1D1E1F1中,连接A1D1,B1E1,C1F1,设交点为O1,易知O1为六边形A1B1C1D1E1F1的中心,四边形A1B1C1O1为平行四边形.
连接A1C1,与B1O1交于点H1,连接HH1,OO1,易知OO1⊥平面ABCDEF,且OO1∥HH1.
由题意以及梯形的中位线性质可得AA1+CC1=2HH1=BB1+OO1,解得OO1=1.3(m),
又BE的中点为O,所以EE1+BB1=2OO1,所以EE1=1.7(m),
同理AA1+DD1=2OO1,解得DD1=1.4(m),
CC1+FF1=2OO1,解得FF1=1.6(m),
所以DD1+EE1+FF1=1.4+1.7+1.6=4.7(m).
故选A.
名师点睛 关键是利用中位线定理列方程求解.
13.D 当截面过底面直径时,截面如题图①;当截面不过底面直径时,截面如题图⑤.
14.答案
解析 如图所示,连接DA1,A1Q,PQ,DP,易知截面为四边形A1DPQ,四边形A1DPQ为等腰梯形,因为正方体A1B1C1D1-ABCD的棱长为2,且P,Q均为所在棱的中点,所以PQ==,DA1==2,PD=A1Q==,所以梯形A1DPQ的高h==,故截面的面积S=×(+2)×=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
