2025人教B版高中数学必修第四册强化练习题(含解析)--11.3.3 平面与平面平行
文档属性
| 名称 | 2025人教B版高中数学必修第四册强化练习题(含解析)--11.3.3 平面与平面平行 |

|
|
| 格式 | docx | ||
| 文件大小 | 725.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第四册
第十一章 立体几何初步
11.3.3 平面与平面平行
基础过关练
题组一 面面平行的判定定理
1.(2022山东济南一中期中)设m,n表示不同的直线,α,β表示不同的平面,则下列结论中正确的是( )
A.若α∥β,m α,n β,则m∥n
B.若m,n是两条异面直线,m∥α,m∥β,n∥α,n∥β,则α∥β
C.若m α,n β,m∥β,n∥α,则α∥β
D.若α∥β,m∥α,n∥m,则n∥β
2.(2024辽宁辽阳期中)设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.以上答案都不对
3.(2023山西晋中月考)下列四个正方体中,A,B,C分别为其所在棱的中点,D,E,F分别为正方体的顶点,则能得出平面ABC∥平面DEF的是( )
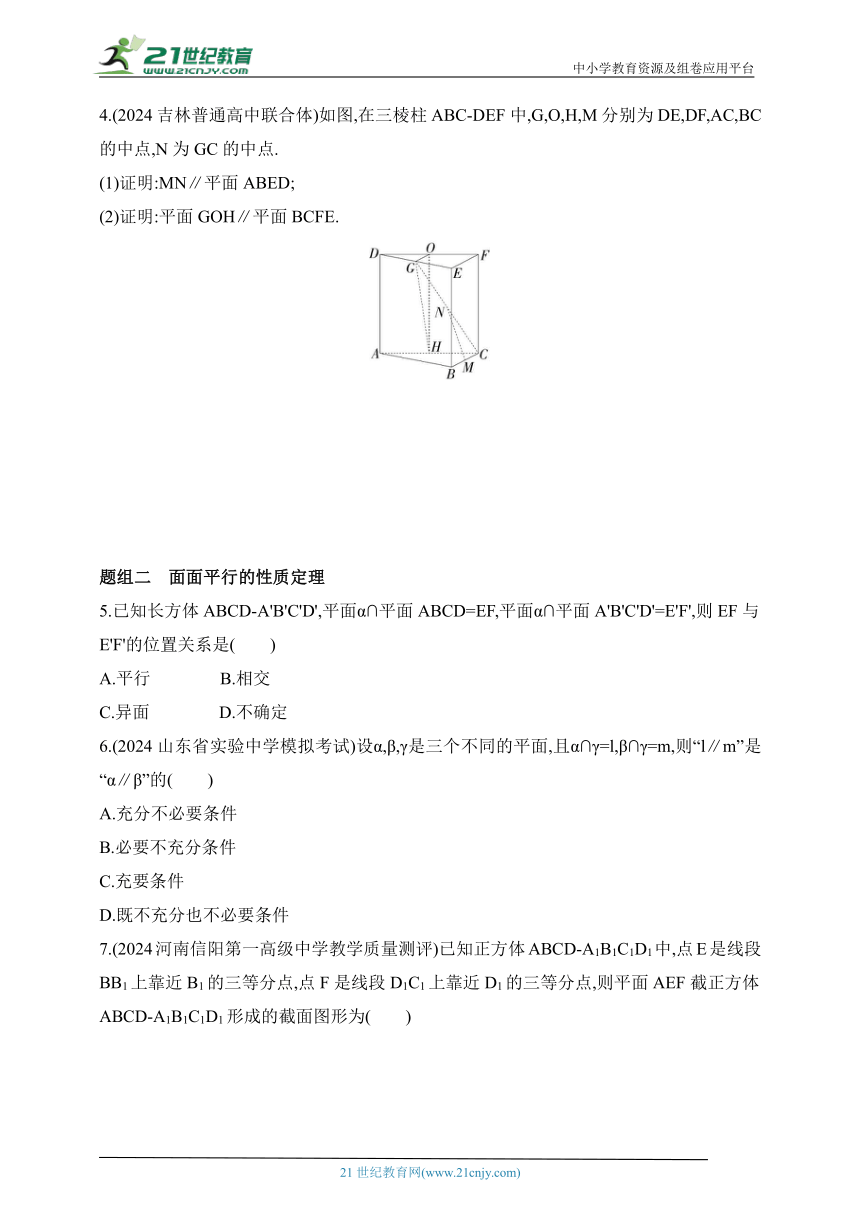
4.(2024吉林普通高中联合体)如图,在三棱柱ABC-DEF中,G,O,H,M分别为DE,DF,AC,BC的中点,N为GC的中点.
(1)证明:MN∥平面ABED;
(2)证明:平面GOH∥平面BCFE.
题组二 面面平行的性质定理
5.已知长方体ABCD-A'B'C'D',平面α∩平面ABCD=EF,平面α∩平面A'B'C'D'=E'F',则EF与E'F'的位置关系是( )
A.平行 B.相交
C.异面 D.不确定
6.(2024山东省实验中学模拟考试)设α,β,γ是三个不同的平面,且α∩γ=l,β∩γ=m,则“l∥m”是“α∥β”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
7.(2024河南信阳第一高级中学教学质量测评)已知正方体ABCD-A1B1C1D1中,点E是线段BB1上靠近B1的三等分点,点F是线段D1C1上靠近D1的三等分点,则平面AEF截正方体ABCD-A1B1C1D1形成的截面图形为( )
A.三角形 B.四边形 C.五边形 D.六边形
8.(2022浙江温州期中)如图,正方体ABCD-A1B1C1D1的棱长为2,E,F,G,H分别为A1B1,AD,B1C1,C1D1的中点,则过GH且与EF平行的平面截正方体所得的截面的面积为( )
A. B.2 C.2 D.4
9.已知平面α∥平面β,P是α,β外一点,过点P作直线m与α,β分别交于A,C两点,过点P作直线n与α,β分别交于B,D两点,且PA=6,AC=9,PD=8,则BD的长为( )
A.16 B.24或
C.14 D.或
10.如图,在长方体ABCD-A1B1C1D1中,过BB1的中点E作一个与平面ACB1平行的平面,交AB于点M,交BC于点N,则= .
11.(2022江苏南京燕子矶中学期中)如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AD∥BC,平面A1DCE与B1B交于点E.
求证:EC∥A1D.
12.在如图所示的几何体中,D是AC的中点,EF∥DB,G,H分别是EC,FB的中点.求证:GH∥平面ABC.
能力提升练
题组一 面面平行的判定定理
1.(2022山西太原期末)如图所示,在正方体ABCD-A1B1C1D1中,E,F,M,N分别为棱AB,BC,DD1,D1C1的中点,则下列判断正确的是 ( )
A.直线AD∥平面MNE
B.直线FC1∥平面MNE
C.平面A1BC∥平面MNE
D.平面AB1D1∥平面MNE
2.(2022北京二中期末)如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内(含边界)一点,若A1P∥平面AEF,则线段A1P长度的取值范围是( )
A. B.
C. D.[,]
3.(2024四川达州外国语学校月考)如图所示,在底面为正方形的四棱锥P-ABCD中,AB=2,PA=4,PB=PD=2,AC与BD相交于点O,E为PD的中点.
(1)求证:EO∥平面PBC;
(2)PA上是否存在点F,使平面OEF∥平面PBC 若存在,请指出F的位置,并给予证明;若不存在,请说明理由.
题组二 面面平行的性质定理
4.用平面α截一个三棱锥,如果截面是梯形,那么平面α必定和这个三棱锥的( )
A.一个侧面平行 B.底面平行
C.仅一条棱平行 D.某两条相对的棱平行
5.(多选题)(2024广西南宁第三十六中学月考)如图,在三棱柱ABC-A1B1C1中,已知点G,H分别在A1B1,A1C1上,且GH经过△A1B1C1的重心,点E,F分别是AB,AC的中点,且平面A1EF∥平面BCHG,则下列结论正确的是( )
A.EF∥GH B.GH∥平面A1EF
C.= D.平面A1EF∥平面BCC1B1
6.(2024山东德州期中)如图,已知四棱锥P-ABCD的底面为平行四边形,M,N,Q分别为PC,CD,AB的中点.
(1)求证:平面MNQ∥平面PAD;
(2)设平面PAD与平面PBC的交线为l,求证:BC∥l.
题组三 面面平行的综合问题
7.(2022河南焦作期末)在四棱锥P-ABCD中,底面ABCD为平行四边形,E是PC的中点,若在棱PD上存在一点F,使得BE∥平面ACF,则=( )
A.3 B.2 C. D.1
8.如图,四棱锥S-ABCD的所有棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
9.(2024黑龙江双鸭山第一中学月考)如图,在正四面体SABC中,AB=4,E,F,R分别是SB,SC,SA的中点,取SE,SF的中点M,N,Q为平面SBC内一点.
(1)求证:平面MNR∥平面AEF;
(2)若RQ∥平面AEF,求线段RQ的最小值.
10.(2022福建莆田五中期中)在三棱柱ABC-A1B1C1中,D为AC的中点,D1是A1C1上的一点.
(1)当等于何值时,平面BC1D∥平面AB1D1 并证明;
(2)当平面BC1D∥平面AB1D1时,记几何体A-A1B1D1,ABD-B1C1D1的体积分别为V1,V2,求V1∶V2.
答案与分层梯度式解析
基础过关练
1.B 对于A,m,n可能异面,故A中结论错误;
对于B,设直线n'∥n,且n'∩m=O,则直线n'和m确定平面γ,又n∥α,n'∥n,n' α,所以n'∥α,又m∥α,n'∩m=O,所以γ∥α,同理可证γ∥β,所以α∥β,故B中结论正确;
对于C,α与β可能相交,故C中结论错误;
对于D,若α∥β,m∥α,n∥m,则n∥β或n β,故D中结论错误.故选B.
2.B 由面面平行的判定定理知B正确;A中,若α内的无数条直线均互相平行,则无法推出α∥β;
C选项可给出反例,如图,
α,β平行于同一条直线m,但α,β不平行.故选B.
3.B 对于A,若平面ABC∥平面DEF,因为AC 平面ABC,所以AC∥平面DEF,由题图可知AC与平面DEF相交,故平面ABC与平面DEF不平行,故A不满足条件;
对于B,易知AC∥EF,AB∥DE,又AC,AB 平面ABC,AB∩AC=A,DE,EF 平面DEF,DE∩EF=E,所以平面ABC∥平面DEF,故B满足条件;
对于C,如图1所示:
图1
在正方体PHDG-MNFE中,易知平面DGEF∥平面MNHP,若平面ABC∥平面DGEF,则平面ABC∥平面MNHP,显然不成立,
因此,平面ABC与平面DGEF不平行,故C不满足条件;
对于D,如图2所示,在正方体PDHG-FNEM中,连接PH,PM,MH,
图2
因为DH∥FM且DH=FM,所以四边形DHMF为平行四边形,所以DF∥MH,
因为DF 平面PHM,MH 平面PHM,
所以DF∥平面PHM,
同理可证EF∥平面PHM,
因为DF∩EF=F,DF,EF 平面DEF,
所以平面DEF∥平面PHM,
若平面ABC∥平面DEF,则平面ABC∥平面PHM,
显然不成立,故平面ABC与平面DEF不平行,故D不满足条件.故选B.
4.证明 (1)如图,连接BG.
∵M为BC的中点,N为GC的中点,∴MN∥BG.
∵BG 平面ABED,MN 平面ABED,
∴MN∥平面ABED.
(2)∵G,O分别为DE,DF的中点,∴GO∥EF.
∵EF 平面BCFE,GO 平面BCFE,∴GO∥平面BCFE.
∵OF∥HC且OF=HC,∴四边形OFCH是平行四边形,∴OH∥FC.
∵FC 平面BCFE,OH 平面BCFE,∴OH∥平面BCFE.
又GO∩OH=O,GO,OH 平面GOH,∴平面GOH∥平面BCFE.
5.A 由面面平行的性质定理易得EF∥E'F'.
6.B 由α∩γ=l,β∩γ=m,l∥m,得α,β相交或平行,
故“l∥m”推不出“α∥β”,
由α∩γ=l,β∩γ=m,α∥β,及面面平行的性质定理知l∥m,故“α∥β”能推出“l∥m”,
故“l∥m”是“α∥β”的必要不充分条件.故选B.
7.C 如图,设正方体的棱长为6,分别延长AE,A1B1交于点G,易知△GB1E∽△GA1A,则==,故B1G=3,连接FG交B1C1于H,连接EH,
设平面AEF与平面DCC1D1的交线为l,则F∈l,
因为平面ABB1A1∥平面DCC1D1,平面AEF∩平面ABB1A1=AE,平面AEF∩平面DCC1D1=l,
所以l∥AE,设l∩D1D=I,则FI∥AE,
此时△FD1I∽△ABE,则==,故ID1=,连接AI,所以五边形AIFHE即为所求截面图形,故选C.
8.C 取AB的中点P,BC的中点M,CD的中点N,连接FP,EP,MN,MG,NH,由正方体的结构特征可得MG NH,且MG⊥HG,所以四边形MGHN为矩形,
又EP∥MG,MG 平面MGHN,EP 平面MGHN,
∴EP∥平面MGHN,
易知FP∥MN,又MN 平面MGHN,FP 平面MGHN,
∴FP∥平面MGHN,
∵EP∩FP=P,EP,FP 平面EFP,
∴平面EFP∥平面MGHN,
又EF 平面EFP,∴EF∥平面MGHN,
∴过GH且与EF平行的平面截正方体所得的截面为矩形MGHN,
∵MG=2,GH==,
∴S矩形MGHN=2.故选C.
9.B 由题意得AB∥CD.分两种情况:
点P在α,β的同侧,则PC=PA+AC=15,=,
∴PB=,∴BD=PD-PB=;
点P在α,β之间,则有PC=AC-PA=3,=,
∴PB=16,∴BD=PB+PD=24.
综上,BD=或BD=24.
10.答案
解析 ∵平面MNE∥平面ACB1,
∴由面面平行的性质定理可得EN∥B1C,EM∥B1A.
又∵E为BB1的中点,
∴M,N分别为BA,BC的中点,
∴MN=AC,即=.
11.证明 因为BE∥AA1,AA1 平面AA1D,BE 平面AA1D,
所以BE∥平面AA1D.
因为BC∥AD,AD 平面AA1D,BC 平面AA1D,
所以BC∥平面AA1D.
又BE∩BC=B,BE,BC 平面BCE,
所以平面BCE∥平面AA1D.
因为平面A1DCE∩平面BCE=EC,平面A1DCE∩平面AA1D=A1D,所以EC∥A1D.
12.证明 如图,取FC的中点I,连接GI,HI,
则有GI∥EF,HI∥BC.
因为EF∥DB,所以GI∥DB.
因为GI∩HI=I,DB∩BC=B,GI,HI 平面GHI,DB,BC 平面ABC,
所以平面GHI∥平面ABC.
因为GH 平面GHI,所以GH∥平面ABC.
能力提升练
1.D 作出过点M,N,E的截面如图所示(其中H,I,J均为所在棱的中点),所以直线AD与平面MNE相交于点H,故A错误;
直线FC1与直线IJ在平面BCC1B1上必定相交,故直线FC1与平面MNE不平行,故B错误;
直线A1B与直线EI相交,故平面A1BC与平面MNE不平行,故C错误;
由直线AB1∥直线EI,直线AD1∥直线HM,易知AB1∥平面MNE,AD1∥平面MNE,又AB1∩AD1=A,AB1,AD1 平面AB1D1,所以平面AB1D1∥平面MNE,故D正确.故选D.
2.B 如图所示,分别取棱BB1,B1C1的中点M,N,连接A1M,A1N,MN,BC1,NE,
∵M,N,E,F分别为所在棱的中点,
∴MN∥BC1,EF∥BC1,∴MN∥EF.
又MN 平面AEF,EF 平面AEF,
∴MN∥平面AEF.
∵AA1∥NE,AA1=NE,
∴四边形AENA1为平行四边形,
∴A1N∥AE.
又A1N 平面AEF,AE 平面AEF,
∴A1N∥平面AEF,
又A1N∩MN=N,A1N,MN 平面A1MN,
∴平面A1MN∥平面AEF.
∵P是侧面BCC1B1内一点,且A1P∥平面AEF,
∴点P必在线段MN上.
在Rt△MB1N中,MN===.在Rt△A1B1M中,A1M===.
同理,在Rt△A1B1N中,可得A1N=,
∴△A1MN为等腰三角形.
设MN的中点为O,连接A1O.
当点P位于MN的中点O时,A1P⊥MN,A1P的长度最短;当点P位于点M或点N时,A1P的长度最长.
易得A1O===,
∴线段A1P长度的取值范围是.
3.解析 (1)证明:因为O,E分别是BD,PD的中点,所以EO∥PB,
又EO 平面PBC,PB 平面PBC,所以EO∥平面PBC.
(2)存在,点F是PA的中点.连接EF,OF.
因为O,F分别是AC,AP的中点,所以OF∥PC,
又OF 平面PBC,PC 平面PBC,
所以OF∥平面PBC.
由(1)可知,EO∥平面PBC,OF∩EO=O,OF,EO 平面OEF,
所以平面OEF∥平面PBC,
所以PA上存在中点F,使平面OEF∥平面PBC.
4.C 当平面α平行于三棱锥的某一面时,截面为三角形,故A,B错误.
如图,当平面α∥SA时,截面是四边形DEFG,
又SA 平面SAB,平面SAB∩平面DEFG=DG,
∴SA∥DG,同理,SA∥EF,∴DG∥EF.
同理,当平面α∥BC时,GF∥DE.
∵截面是梯形,
∴四边形DEFG中仅有一组对边平行,
故平面α仅与一条棱平行.故选C.
5.ABC 由三棱柱的结构特点可知平面ABC∥平面A1B1C1,
又平面BCHG∩平面ABC=BC,平面BCHG∩平面A1B1C1=GH,所以由面面平行的性质定理可知BC∥GH,
又点E,F分别是AB,AC的中点,所以BC∥EF,所以EF∥GH,所以A正确;
因为EF∥GH,EF 平面A1EF,GH 平面A1EF,所以GH∥平面A1EF,所以B正确;
又GH经过△A1B1C1的重心,
所以==,
又BC∥EF,=,所以=,所以C正确;
因为平面A1EF∥平面BCHG,平面BCHG与平面BCC1B1相交,所以平面A1EF与平面BCC1B1相交,因此D错误.
6.证明 (1)因为M,N,Q分别为PC,CD,AB的中点,底面ABCD为平行四边形,
所以MN∥PD,NQ∥AD,
又MN 平面PAD,PD 平面PAD,
所以MN∥平面PAD,
同理可得NQ∥平面PAD,
又MN∩NQ=N,MN,NQ 平面MNQ,
所以平面MNQ∥平面PAD.
(2)因为BC∥AD,BC 平面PAD,AD 平面PAD,
所以BC∥平面PAD,
又BC 平面PBC,平面PBC∩平面PAD=l,
所以BC∥l.
7.B 连接BD,与AC相交于点O,连接FO,取PF的中点M,连接ME,MB,
因为E,M分别为PC,PF的中点,
所以ME是△PFC的中位线,
所以ME∥FC,
又FC 平面ACF,ME 平面ACF,
所以ME∥平面ACF.
当F为MD的中点,即DF=FM=MP,也即=2时,
由O为BD的中点,得FO∥MB,
因为FO 平面ACF,MB 平面ACF,
所以MB∥平面ACF,
又ME∩MB=M,ME,MB 平面MBE,
所以平面ACF∥平面MBE,
又BE 平面MBE,所以BE∥平面ACF.
即在棱PD上存在一点F,当=2时,BE∥平面ACF.
8.C ∵AB=BC=CD=AD=2,
∴四边形ABCD为菱形,∴CD∥AB.
又∵CD 平面SAB,AB 平面SAB,∴CD∥平面SAB.
又∵CD 平面CDEF,平面CDEF∩平面SAB=EF,
∴CD∥EF,∴EF∥AB.
又∵E为SA的中点,∴F为SB的中点,
∴EF=AB=1.
∵△SAD和△SBC都是等边三角形,
∴DE=CF=2×sin 60°=,
∴四边形DEFC的周长为CD+DE+EF+FC=2++1+=3+2.
9.解析 (1)证明:因为R,M,N分别是SA,SE,SF的中点,所以MN∥EF,
又MN 平面AEF,EF 平面AEF,
所以MN∥平面AEF.同理,MR∥平面AEF,
又因为MR∩MN=M,MR,MN 平面MNR,
所以平面MNR∥平面AEF.
(2)由(1)可得平面MNR∥平面AEF,若RQ∥平面AEF,则点Q在线段MN上移动,
在△RMN中,RM=AE=,RN=AF=,MN=1,RQ的最小值为R到线段MN的距离,
因为△RMN是等腰三角形,所以RQ的最小值为=.
10.解析 (1)当=1时,平面BC1D∥平面AB1D1.证明如下:因为D,D1分别是AC,A1C1的中点,
所以AD∥D1C1,且AD=D1C1,
所以四边形ADC1D1是平行四边形,所以AD1∥DC1.
因为DC1 平面AB1D1,AD1 平面AB1D1,
所以DC1∥平面AB1D1.
连接DD1,易知DD1∥BB1,且DD1=BB1,
所以四边形BDD1B1是平行四边形,所以BD∥B1D1.
因为BD 平面AB1D1,B1D1 平面AB1D1,
所以BD∥平面AB1D1,
又DC1∩BD=D,DC1,BD 平面BC1D,
所以平面BC1D∥平面AB1D1.
(2)设三棱柱ABC-A1B1C1的高为h.易知V1=··h,=S△BCD·h,
由(1)知,D1是线段A1C1的中点,所以=S△BCD,所以V1=.
又=S△ABC·h,且S△ABC=2S△BCD,
所以=6V1,
故V2=-V1-=4V1,
所以V1∶V2=1∶4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第四册
第十一章 立体几何初步
11.3.3 平面与平面平行
基础过关练
题组一 面面平行的判定定理
1.(2022山东济南一中期中)设m,n表示不同的直线,α,β表示不同的平面,则下列结论中正确的是( )
A.若α∥β,m α,n β,则m∥n
B.若m,n是两条异面直线,m∥α,m∥β,n∥α,n∥β,则α∥β
C.若m α,n β,m∥β,n∥α,则α∥β
D.若α∥β,m∥α,n∥m,则n∥β
2.(2024辽宁辽阳期中)设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.以上答案都不对
3.(2023山西晋中月考)下列四个正方体中,A,B,C分别为其所在棱的中点,D,E,F分别为正方体的顶点,则能得出平面ABC∥平面DEF的是( )
4.(2024吉林普通高中联合体)如图,在三棱柱ABC-DEF中,G,O,H,M分别为DE,DF,AC,BC的中点,N为GC的中点.
(1)证明:MN∥平面ABED;
(2)证明:平面GOH∥平面BCFE.
题组二 面面平行的性质定理
5.已知长方体ABCD-A'B'C'D',平面α∩平面ABCD=EF,平面α∩平面A'B'C'D'=E'F',则EF与E'F'的位置关系是( )
A.平行 B.相交
C.异面 D.不确定
6.(2024山东省实验中学模拟考试)设α,β,γ是三个不同的平面,且α∩γ=l,β∩γ=m,则“l∥m”是“α∥β”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
7.(2024河南信阳第一高级中学教学质量测评)已知正方体ABCD-A1B1C1D1中,点E是线段BB1上靠近B1的三等分点,点F是线段D1C1上靠近D1的三等分点,则平面AEF截正方体ABCD-A1B1C1D1形成的截面图形为( )
A.三角形 B.四边形 C.五边形 D.六边形
8.(2022浙江温州期中)如图,正方体ABCD-A1B1C1D1的棱长为2,E,F,G,H分别为A1B1,AD,B1C1,C1D1的中点,则过GH且与EF平行的平面截正方体所得的截面的面积为( )
A. B.2 C.2 D.4
9.已知平面α∥平面β,P是α,β外一点,过点P作直线m与α,β分别交于A,C两点,过点P作直线n与α,β分别交于B,D两点,且PA=6,AC=9,PD=8,则BD的长为( )
A.16 B.24或
C.14 D.或
10.如图,在长方体ABCD-A1B1C1D1中,过BB1的中点E作一个与平面ACB1平行的平面,交AB于点M,交BC于点N,则= .
11.(2022江苏南京燕子矶中学期中)如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AD∥BC,平面A1DCE与B1B交于点E.
求证:EC∥A1D.
12.在如图所示的几何体中,D是AC的中点,EF∥DB,G,H分别是EC,FB的中点.求证:GH∥平面ABC.
能力提升练
题组一 面面平行的判定定理
1.(2022山西太原期末)如图所示,在正方体ABCD-A1B1C1D1中,E,F,M,N分别为棱AB,BC,DD1,D1C1的中点,则下列判断正确的是 ( )
A.直线AD∥平面MNE
B.直线FC1∥平面MNE
C.平面A1BC∥平面MNE
D.平面AB1D1∥平面MNE
2.(2022北京二中期末)如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内(含边界)一点,若A1P∥平面AEF,则线段A1P长度的取值范围是( )
A. B.
C. D.[,]
3.(2024四川达州外国语学校月考)如图所示,在底面为正方形的四棱锥P-ABCD中,AB=2,PA=4,PB=PD=2,AC与BD相交于点O,E为PD的中点.
(1)求证:EO∥平面PBC;
(2)PA上是否存在点F,使平面OEF∥平面PBC 若存在,请指出F的位置,并给予证明;若不存在,请说明理由.
题组二 面面平行的性质定理
4.用平面α截一个三棱锥,如果截面是梯形,那么平面α必定和这个三棱锥的( )
A.一个侧面平行 B.底面平行
C.仅一条棱平行 D.某两条相对的棱平行
5.(多选题)(2024广西南宁第三十六中学月考)如图,在三棱柱ABC-A1B1C1中,已知点G,H分别在A1B1,A1C1上,且GH经过△A1B1C1的重心,点E,F分别是AB,AC的中点,且平面A1EF∥平面BCHG,则下列结论正确的是( )
A.EF∥GH B.GH∥平面A1EF
C.= D.平面A1EF∥平面BCC1B1
6.(2024山东德州期中)如图,已知四棱锥P-ABCD的底面为平行四边形,M,N,Q分别为PC,CD,AB的中点.
(1)求证:平面MNQ∥平面PAD;
(2)设平面PAD与平面PBC的交线为l,求证:BC∥l.
题组三 面面平行的综合问题
7.(2022河南焦作期末)在四棱锥P-ABCD中,底面ABCD为平行四边形,E是PC的中点,若在棱PD上存在一点F,使得BE∥平面ACF,则=( )
A.3 B.2 C. D.1
8.如图,四棱锥S-ABCD的所有棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
9.(2024黑龙江双鸭山第一中学月考)如图,在正四面体SABC中,AB=4,E,F,R分别是SB,SC,SA的中点,取SE,SF的中点M,N,Q为平面SBC内一点.
(1)求证:平面MNR∥平面AEF;
(2)若RQ∥平面AEF,求线段RQ的最小值.
10.(2022福建莆田五中期中)在三棱柱ABC-A1B1C1中,D为AC的中点,D1是A1C1上的一点.
(1)当等于何值时,平面BC1D∥平面AB1D1 并证明;
(2)当平面BC1D∥平面AB1D1时,记几何体A-A1B1D1,ABD-B1C1D1的体积分别为V1,V2,求V1∶V2.
答案与分层梯度式解析
基础过关练
1.B 对于A,m,n可能异面,故A中结论错误;
对于B,设直线n'∥n,且n'∩m=O,则直线n'和m确定平面γ,又n∥α,n'∥n,n' α,所以n'∥α,又m∥α,n'∩m=O,所以γ∥α,同理可证γ∥β,所以α∥β,故B中结论正确;
对于C,α与β可能相交,故C中结论错误;
对于D,若α∥β,m∥α,n∥m,则n∥β或n β,故D中结论错误.故选B.
2.B 由面面平行的判定定理知B正确;A中,若α内的无数条直线均互相平行,则无法推出α∥β;
C选项可给出反例,如图,
α,β平行于同一条直线m,但α,β不平行.故选B.
3.B 对于A,若平面ABC∥平面DEF,因为AC 平面ABC,所以AC∥平面DEF,由题图可知AC与平面DEF相交,故平面ABC与平面DEF不平行,故A不满足条件;
对于B,易知AC∥EF,AB∥DE,又AC,AB 平面ABC,AB∩AC=A,DE,EF 平面DEF,DE∩EF=E,所以平面ABC∥平面DEF,故B满足条件;
对于C,如图1所示:
图1
在正方体PHDG-MNFE中,易知平面DGEF∥平面MNHP,若平面ABC∥平面DGEF,则平面ABC∥平面MNHP,显然不成立,
因此,平面ABC与平面DGEF不平行,故C不满足条件;
对于D,如图2所示,在正方体PDHG-FNEM中,连接PH,PM,MH,
图2
因为DH∥FM且DH=FM,所以四边形DHMF为平行四边形,所以DF∥MH,
因为DF 平面PHM,MH 平面PHM,
所以DF∥平面PHM,
同理可证EF∥平面PHM,
因为DF∩EF=F,DF,EF 平面DEF,
所以平面DEF∥平面PHM,
若平面ABC∥平面DEF,则平面ABC∥平面PHM,
显然不成立,故平面ABC与平面DEF不平行,故D不满足条件.故选B.
4.证明 (1)如图,连接BG.
∵M为BC的中点,N为GC的中点,∴MN∥BG.
∵BG 平面ABED,MN 平面ABED,
∴MN∥平面ABED.
(2)∵G,O分别为DE,DF的中点,∴GO∥EF.
∵EF 平面BCFE,GO 平面BCFE,∴GO∥平面BCFE.
∵OF∥HC且OF=HC,∴四边形OFCH是平行四边形,∴OH∥FC.
∵FC 平面BCFE,OH 平面BCFE,∴OH∥平面BCFE.
又GO∩OH=O,GO,OH 平面GOH,∴平面GOH∥平面BCFE.
5.A 由面面平行的性质定理易得EF∥E'F'.
6.B 由α∩γ=l,β∩γ=m,l∥m,得α,β相交或平行,
故“l∥m”推不出“α∥β”,
由α∩γ=l,β∩γ=m,α∥β,及面面平行的性质定理知l∥m,故“α∥β”能推出“l∥m”,
故“l∥m”是“α∥β”的必要不充分条件.故选B.
7.C 如图,设正方体的棱长为6,分别延长AE,A1B1交于点G,易知△GB1E∽△GA1A,则==,故B1G=3,连接FG交B1C1于H,连接EH,
设平面AEF与平面DCC1D1的交线为l,则F∈l,
因为平面ABB1A1∥平面DCC1D1,平面AEF∩平面ABB1A1=AE,平面AEF∩平面DCC1D1=l,
所以l∥AE,设l∩D1D=I,则FI∥AE,
此时△FD1I∽△ABE,则==,故ID1=,连接AI,所以五边形AIFHE即为所求截面图形,故选C.
8.C 取AB的中点P,BC的中点M,CD的中点N,连接FP,EP,MN,MG,NH,由正方体的结构特征可得MG NH,且MG⊥HG,所以四边形MGHN为矩形,
又EP∥MG,MG 平面MGHN,EP 平面MGHN,
∴EP∥平面MGHN,
易知FP∥MN,又MN 平面MGHN,FP 平面MGHN,
∴FP∥平面MGHN,
∵EP∩FP=P,EP,FP 平面EFP,
∴平面EFP∥平面MGHN,
又EF 平面EFP,∴EF∥平面MGHN,
∴过GH且与EF平行的平面截正方体所得的截面为矩形MGHN,
∵MG=2,GH==,
∴S矩形MGHN=2.故选C.
9.B 由题意得AB∥CD.分两种情况:
点P在α,β的同侧,则PC=PA+AC=15,=,
∴PB=,∴BD=PD-PB=;
点P在α,β之间,则有PC=AC-PA=3,=,
∴PB=16,∴BD=PB+PD=24.
综上,BD=或BD=24.
10.答案
解析 ∵平面MNE∥平面ACB1,
∴由面面平行的性质定理可得EN∥B1C,EM∥B1A.
又∵E为BB1的中点,
∴M,N分别为BA,BC的中点,
∴MN=AC,即=.
11.证明 因为BE∥AA1,AA1 平面AA1D,BE 平面AA1D,
所以BE∥平面AA1D.
因为BC∥AD,AD 平面AA1D,BC 平面AA1D,
所以BC∥平面AA1D.
又BE∩BC=B,BE,BC 平面BCE,
所以平面BCE∥平面AA1D.
因为平面A1DCE∩平面BCE=EC,平面A1DCE∩平面AA1D=A1D,所以EC∥A1D.
12.证明 如图,取FC的中点I,连接GI,HI,
则有GI∥EF,HI∥BC.
因为EF∥DB,所以GI∥DB.
因为GI∩HI=I,DB∩BC=B,GI,HI 平面GHI,DB,BC 平面ABC,
所以平面GHI∥平面ABC.
因为GH 平面GHI,所以GH∥平面ABC.
能力提升练
1.D 作出过点M,N,E的截面如图所示(其中H,I,J均为所在棱的中点),所以直线AD与平面MNE相交于点H,故A错误;
直线FC1与直线IJ在平面BCC1B1上必定相交,故直线FC1与平面MNE不平行,故B错误;
直线A1B与直线EI相交,故平面A1BC与平面MNE不平行,故C错误;
由直线AB1∥直线EI,直线AD1∥直线HM,易知AB1∥平面MNE,AD1∥平面MNE,又AB1∩AD1=A,AB1,AD1 平面AB1D1,所以平面AB1D1∥平面MNE,故D正确.故选D.
2.B 如图所示,分别取棱BB1,B1C1的中点M,N,连接A1M,A1N,MN,BC1,NE,
∵M,N,E,F分别为所在棱的中点,
∴MN∥BC1,EF∥BC1,∴MN∥EF.
又MN 平面AEF,EF 平面AEF,
∴MN∥平面AEF.
∵AA1∥NE,AA1=NE,
∴四边形AENA1为平行四边形,
∴A1N∥AE.
又A1N 平面AEF,AE 平面AEF,
∴A1N∥平面AEF,
又A1N∩MN=N,A1N,MN 平面A1MN,
∴平面A1MN∥平面AEF.
∵P是侧面BCC1B1内一点,且A1P∥平面AEF,
∴点P必在线段MN上.
在Rt△MB1N中,MN===.在Rt△A1B1M中,A1M===.
同理,在Rt△A1B1N中,可得A1N=,
∴△A1MN为等腰三角形.
设MN的中点为O,连接A1O.
当点P位于MN的中点O时,A1P⊥MN,A1P的长度最短;当点P位于点M或点N时,A1P的长度最长.
易得A1O===,
∴线段A1P长度的取值范围是.
3.解析 (1)证明:因为O,E分别是BD,PD的中点,所以EO∥PB,
又EO 平面PBC,PB 平面PBC,所以EO∥平面PBC.
(2)存在,点F是PA的中点.连接EF,OF.
因为O,F分别是AC,AP的中点,所以OF∥PC,
又OF 平面PBC,PC 平面PBC,
所以OF∥平面PBC.
由(1)可知,EO∥平面PBC,OF∩EO=O,OF,EO 平面OEF,
所以平面OEF∥平面PBC,
所以PA上存在中点F,使平面OEF∥平面PBC.
4.C 当平面α平行于三棱锥的某一面时,截面为三角形,故A,B错误.
如图,当平面α∥SA时,截面是四边形DEFG,
又SA 平面SAB,平面SAB∩平面DEFG=DG,
∴SA∥DG,同理,SA∥EF,∴DG∥EF.
同理,当平面α∥BC时,GF∥DE.
∵截面是梯形,
∴四边形DEFG中仅有一组对边平行,
故平面α仅与一条棱平行.故选C.
5.ABC 由三棱柱的结构特点可知平面ABC∥平面A1B1C1,
又平面BCHG∩平面ABC=BC,平面BCHG∩平面A1B1C1=GH,所以由面面平行的性质定理可知BC∥GH,
又点E,F分别是AB,AC的中点,所以BC∥EF,所以EF∥GH,所以A正确;
因为EF∥GH,EF 平面A1EF,GH 平面A1EF,所以GH∥平面A1EF,所以B正确;
又GH经过△A1B1C1的重心,
所以==,
又BC∥EF,=,所以=,所以C正确;
因为平面A1EF∥平面BCHG,平面BCHG与平面BCC1B1相交,所以平面A1EF与平面BCC1B1相交,因此D错误.
6.证明 (1)因为M,N,Q分别为PC,CD,AB的中点,底面ABCD为平行四边形,
所以MN∥PD,NQ∥AD,
又MN 平面PAD,PD 平面PAD,
所以MN∥平面PAD,
同理可得NQ∥平面PAD,
又MN∩NQ=N,MN,NQ 平面MNQ,
所以平面MNQ∥平面PAD.
(2)因为BC∥AD,BC 平面PAD,AD 平面PAD,
所以BC∥平面PAD,
又BC 平面PBC,平面PBC∩平面PAD=l,
所以BC∥l.
7.B 连接BD,与AC相交于点O,连接FO,取PF的中点M,连接ME,MB,
因为E,M分别为PC,PF的中点,
所以ME是△PFC的中位线,
所以ME∥FC,
又FC 平面ACF,ME 平面ACF,
所以ME∥平面ACF.
当F为MD的中点,即DF=FM=MP,也即=2时,
由O为BD的中点,得FO∥MB,
因为FO 平面ACF,MB 平面ACF,
所以MB∥平面ACF,
又ME∩MB=M,ME,MB 平面MBE,
所以平面ACF∥平面MBE,
又BE 平面MBE,所以BE∥平面ACF.
即在棱PD上存在一点F,当=2时,BE∥平面ACF.
8.C ∵AB=BC=CD=AD=2,
∴四边形ABCD为菱形,∴CD∥AB.
又∵CD 平面SAB,AB 平面SAB,∴CD∥平面SAB.
又∵CD 平面CDEF,平面CDEF∩平面SAB=EF,
∴CD∥EF,∴EF∥AB.
又∵E为SA的中点,∴F为SB的中点,
∴EF=AB=1.
∵△SAD和△SBC都是等边三角形,
∴DE=CF=2×sin 60°=,
∴四边形DEFC的周长为CD+DE+EF+FC=2++1+=3+2.
9.解析 (1)证明:因为R,M,N分别是SA,SE,SF的中点,所以MN∥EF,
又MN 平面AEF,EF 平面AEF,
所以MN∥平面AEF.同理,MR∥平面AEF,
又因为MR∩MN=M,MR,MN 平面MNR,
所以平面MNR∥平面AEF.
(2)由(1)可得平面MNR∥平面AEF,若RQ∥平面AEF,则点Q在线段MN上移动,
在△RMN中,RM=AE=,RN=AF=,MN=1,RQ的最小值为R到线段MN的距离,
因为△RMN是等腰三角形,所以RQ的最小值为=.
10.解析 (1)当=1时,平面BC1D∥平面AB1D1.证明如下:因为D,D1分别是AC,A1C1的中点,
所以AD∥D1C1,且AD=D1C1,
所以四边形ADC1D1是平行四边形,所以AD1∥DC1.
因为DC1 平面AB1D1,AD1 平面AB1D1,
所以DC1∥平面AB1D1.
连接DD1,易知DD1∥BB1,且DD1=BB1,
所以四边形BDD1B1是平行四边形,所以BD∥B1D1.
因为BD 平面AB1D1,B1D1 平面AB1D1,
所以BD∥平面AB1D1,
又DC1∩BD=D,DC1,BD 平面BC1D,
所以平面BC1D∥平面AB1D1.
(2)设三棱柱ABC-A1B1C1的高为h.易知V1=··h,=S△BCD·h,
由(1)知,D1是线段A1C1的中点,所以=S△BCD,所以V1=.
又=S△ABC·h,且S△ABC=2S△BCD,
所以=6V1,
故V2=-V1-=4V1,
所以V1∶V2=1∶4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
