2025人教B版高中数学必修第四册强化练习题(含解析)--11.4.2 平面与平面垂直
文档属性
| 名称 | 2025人教B版高中数学必修第四册强化练习题(含解析)--11.4.2 平面与平面垂直 |

|
|
| 格式 | docx | ||
| 文件大小 | 671.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 11:12:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第四册
第十一章 立体几何初步
11.4 空间中的垂直关系
11.4.2 平面与平面垂直
基础过关练
题组一 二面角
1.(2023黑龙江牡丹江期末)从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角的关系是( )
A.互为余角 B.相等 C.其和为周角 D.互为补角
2.(2024湖北武汉部分重点中学期中)在四面体ABCD中,已知△ABD为等边三角形,△ABC为等腰直角三角形,斜边AB=4,CD=2,则二面角C-AB-D的大小为( )
A. B. C. D.
3.(2023北京朝阳期末)如图,正方体ABCD-A1B1C1D1的棱长为2,则二面角A1-BD-A的正弦值为 .
4.(2022山东威海期末)已知正方形ABCD的边长为2,E,F分别是边AB,CD的中点,沿EF将四边形AEFD折起,使二面角A-EF-B的大小为60°,则A,C两点间的距离为 .
题组二 平面与平面垂直的判定
5.(2024江西南昌第二中学期末)已知α,β是空间两个不同的平
面,m,n是空间两条不同的直线,则下列说法正确的是( )
A.若m∥α,n∥β,且m∥n,则α∥β
B.若m∥α,n∥β,且m⊥n,则α⊥β
C.若m⊥α,n∥β,且m⊥n,则α⊥β
D.若m⊥α,n⊥β,且m⊥n,则α⊥β
6.(2024上海格致中学期中)给出下列命题,其中是假命题是( )
A.存在每个面都是直角三角形的四面体
B.若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直
C.在四棱柱中,若过相对侧棱的两个截面都垂直于底面,则该四棱柱为直四棱柱
D.棱柱的侧棱都相等,侧面都是全等的平行四边形
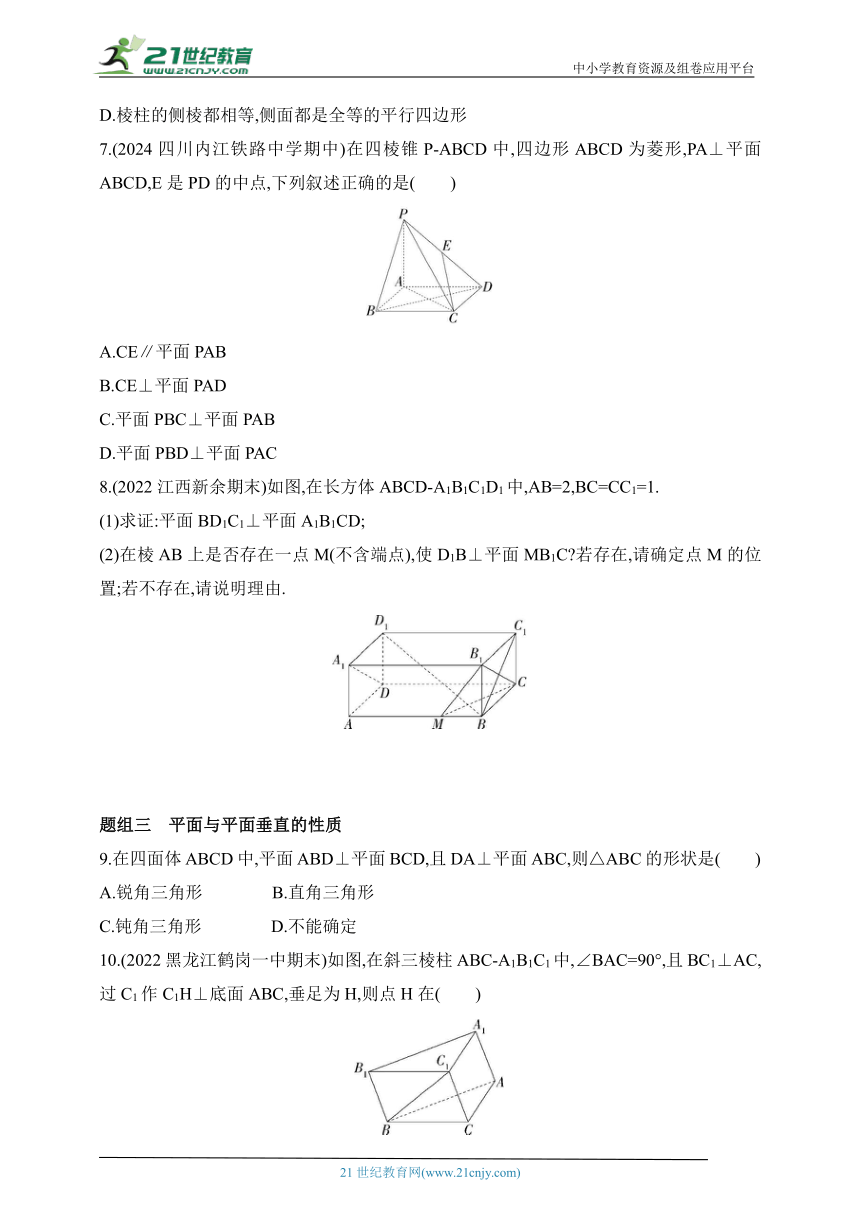
7.(2024四川内江铁路中学期中)在四棱锥P-ABCD中,四边形ABCD为菱形,PA⊥平面ABCD,E是PD的中点,下列叙述正确的是( )
A.CE∥平面PAB
B.CE⊥平面PAD
C.平面PBC⊥平面PAB
D.平面PBD⊥平面PAC
8.(2022江西新余期末)如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1.
(1)求证:平面BD1C1⊥平面A1B1CD;
(2)在棱AB上是否存在一点M(不含端点),使D1B⊥平面MB1C 若存在,请确定点M的位置;若不存在,请说明理由.
题组三 平面与平面垂直的性质
9.在四面体ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
10.(2022黑龙江鹤岗一中期末)如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( )
A.直线AC上 B.直线AB上
C.直线BC上 D.△ABC内部
11.(2023山西忻州期末)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到三棱锥D-ABC(如图2).求证:BC⊥平面ADC.
图1 图2
12.(2024四川成都三诊)如图,在三棱台ABC-DEF中,H在AC边上,平面ACFD⊥平面ABC,∠ACD=60°,CH=2,CD=4,BC=,BH⊥BC.
(1)证明:EF⊥BD;
(2)若△ABC的面积为,求三棱锥D-ABH的体积.
能力提升练
题组一 二面角
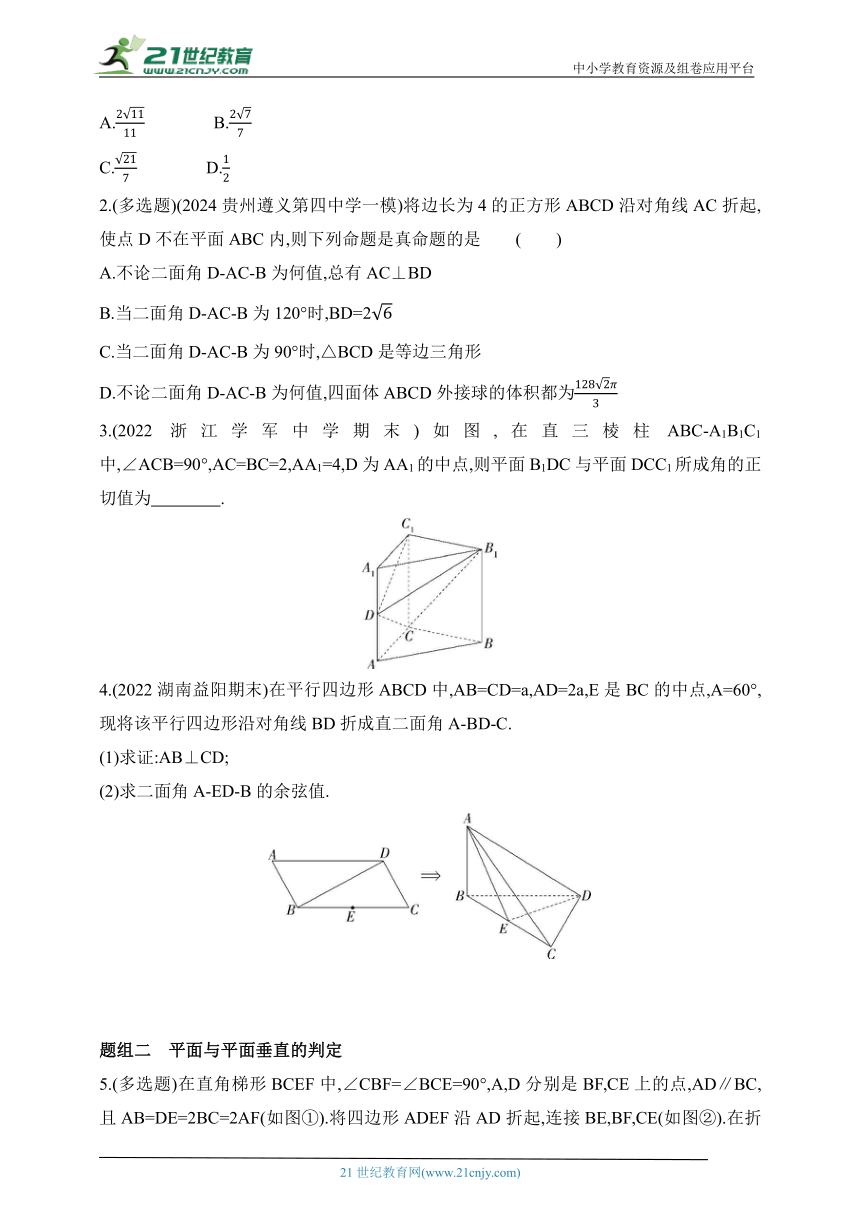
1.(2023湖北黄冈期末)已知在大小为的二面角α-l-β中,A∈α,B∈β,AC⊥l于点C,BD⊥l于点D,且CD=BD=2AC=2,则直线AB与CD所成角的余弦值为( )
A. B.
C. D.
2.(多选题)(2024贵州遵义第四中学一模)将边长为4的正方形ABCD沿对角线AC折起,使点D不在平面ABC内,则下列命题是真命题的是 ( )
A.不论二面角D-AC-B为何值,总有AC⊥BD
B.当二面角D-AC-B为120°时,BD=2
C.当二面角D-AC-B为90°时,△BCD是等边三角形
D.不论二面角D-AC-B为何值,四面体ABCD外接球的体积都为
3.(2022浙江学军中学期末)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,D为AA1的中点,则平面B1DC与平面DCC1所成角的正切值为 .
4.(2022湖南益阳期末)在平行四边形ABCD中,AB=CD=a,AD=2a,E是BC的中点,A=60°,现将该平行四边形沿对角线BD折成直二面角A-BD-C.
(1)求证:AB⊥CD;
(2)求二面角A-ED-B的余弦值.
题组二 平面与平面垂直的判定
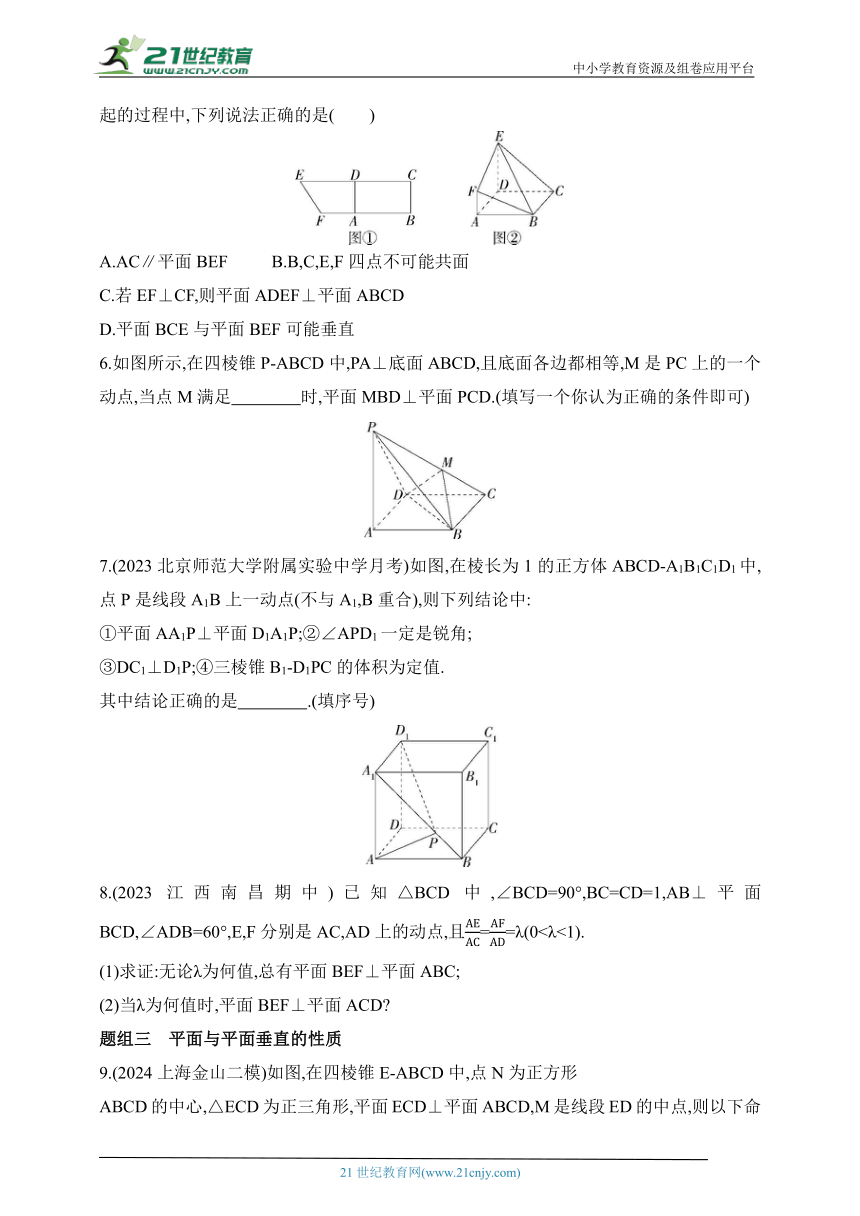
5.(多选题)在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图①).将四边形ADEF沿AD折起,连接BE,BF,CE(如图②).在折起的过程中,下列说法正确的是( )
A.AC∥平面BEF B.B,C,E,F四点不可能共面
C.若EF⊥CF,则平面ADEF⊥平面ABCD
D.平面BCE与平面BEF可能垂直
6.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一个动点,当点M满足 时,平面MBD⊥平面PCD.(填写一个你认为正确的条件即可)
7.(2023北京师范大学附属实验中学月考)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P是线段A1B上一动点(不与A1,B重合),则下列结论中:
①平面AA1P⊥平面D1A1P;②∠APD1一定是锐角;
③DC1⊥D1P;④三棱锥B1-D1PC的体积为定值.
其中结论正确的是 .(填序号)
8.(2023江西南昌期中)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且==λ(0<λ<1).
(1)求证:无论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD
题组三 平面与平面垂直的性质
9.(2024上海金山二模)如图,在四棱锥E-ABCD中,点N为正方形
ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则以下命题中正确的是( )
A.BM=EN B.CD⊥MN
C.A,M,N三点共线 D.直线BM与EN相交
10.(多选题)(2024山东聊城二模)已知四棱锥P-ABCD的底面ABCD是正方形,则下列关系能同时成立的是( )
A.“AB=PB”与“PB=BD”
B.“PA⊥PC”与“PB⊥PD”
C.“PB⊥CD”与“PC⊥AB”
D.“平面PAB⊥平面PBD”与“平面PCD⊥平面PBD”
11.(2022江西南昌八一中学等名校期末)如图,平面ABE⊥平面ABC,△ABC是等边三角形,D为AB的中点,BC=CF=2,FA=FB=2,EA=EB.
(1)证明:DE∥CF;
(2)求三棱锥C-BEF的体积.
答案与分层梯度式解析
基础过关练
1.D 如图,A为二面角α-l-β内任意一点,AB⊥α,AC⊥β,过B作BD⊥l于D,
连接CD,因为AB⊥α,l α,所以AB⊥l,
因为AC⊥β,l β,所以AC⊥l,且AB∩AC=A,
所以l⊥平面ABCD,且CD 平面ABCD,所以l⊥CD,
则∠BDC为二面角α-l-β的平面角,
又∠ABD=∠ACD=90°,∠BAC为两条垂线AB与AC所成的角,所以∠A+∠BDC=180°,
所以两条垂线所夹的角与二面角的平面角互为补角.
故选D.
2.A 取AB的中点O,连接CO,DO,如图,
由AD=BD=AB=4,AC=BC,∠ACB=90°,得OC⊥AB,OD⊥AB,
因此∠COD是二面角C-AB-D的平面角,
在△COD中,OC=2,OD=2,CD=2,
由余弦定理得cos∠COD===-,
又0≤∠COD≤π,
所以∠COD=,
所以二面角C-AB-D的大小为.故选A.
3.答案
解析 如图,连接AC交BD于点O,连接A1O,
在正方体ABCD-A1B1C1D1中,O为BD的中点,所以AO⊥BD,又A1D=A1B,所以A1O⊥BD,所以∠A1OA即为二面角A1-BD-A的平面角,
又AO=AC==,AA1=2,
所以A1O==,
所以sin∠A1OA===,
即二面角A1-BD-A的正弦值为.
4.答案
解析 如图,连接AB,AC,取BE的中点G,连接AG,CG,由题意得EF⊥AE,EF⊥BE,所以∠AEB是二面角A-EF-B的平面角,则∠AEB=60°,又AE=BE=1,所以△ABE是正三角形,于是AG⊥BE,AG=.
根据EF⊥AE,EF⊥BE,AE∩BE=E,可得EF⊥平面ABE,又AG 平面ABE,所以EF⊥AG,又AG⊥BE,BE∩EF=E,所以AG⊥平面BCFE,又GC 平面BCFE,所以AG⊥GC,又GC2=BC2+BG2=,
所以AC===.
5.D 对于A,若m∥α,n∥β,且m∥n,则α,β可能相交或平行,故A错误;
对于B,若m∥α,n∥β,且m⊥n,则α,β可能相交或平行,故B错误;
对于C,若m⊥α,n∥β,且m⊥n,则α,β可能相交或平行,故C错误;
对于D,若m⊥α,m⊥n,则n在平面α内或n∥α,又n⊥β,所以α⊥β,故D正确.
故选D.
6.D 对于A,如图,在正方体ABCD-A1B1C1D1中,
三棱锥C1-ABC的四个面均为直角三角形,故A是真命题.
对于B,如图,在三棱锥P-ABC中,CA⊥CP,CA⊥CB,CP⊥CB,
因为CA⊥CP,CA⊥CB,且CP∩CB=C,CP,CB 平面PBC,所以CA⊥平面PBC,
又CA 平面PAC,所以平面PAC⊥平面PBC.
同理可得,平面PAC⊥平面ABC,平面ABC⊥平面PBC,故B是真命题.
对于C,如图,平面ACC1A1⊥平面ABCD,平面BDD1B1⊥平面ABCD,平面ACC1A1∩平面BDD1B1=OO1,
所以OO1⊥平面ABCD,易知OO1∥AA1,则AA1⊥平面ABCD,故C是真命题.
对于D,根据棱柱的定义可得,棱柱的侧棱都相等,侧面都是平行四边形,但是不一定全等,故D是假命题.
故选D.
7.D 对于A,∵四边形ABCD是菱形,
∴CD∥AB,
∵CD 平面PAB,AB 平面PAB,
∴CD∥平面PAB,假设CE∥平面PAB,
∵CE∩CD=C,CE,CD 平面PCD,
∴平面PCD∥平面PAB,显然不成立,故假设不成立,故A错误;
对于B,过点C作CF⊥AD,垂足为点F,
∵PA⊥平面ABCD,CF 平面ABCD,
∴CF⊥PA,∵CF⊥AD,PA∩AD=A,PA,AD 平面PAD,
∴CF⊥平面PAD,
∵过C作平面PAD的垂线有且只有一条,
∴CE与平面PAD不垂直,故B错误;
对于C,过点C作CM⊥AB,垂足为点M,
∵PA⊥平面ABCD,CM 平面ABCD,∴CM⊥PA,
∵CM⊥AB,PA∩AB=A,PA,AB 平面PAB,∴CM⊥平面PAB,
若平面PBC⊥平面PAB,过点C作CN⊥PB,垂足为N,
∵平面PBC⊥平面PAB,平面PBC∩平面PAB=PB,CN 平面PBC,∴CN⊥平面PAB,
∵过点C作平面PAB的垂线有且只有一条,
∴CM,CN重合,
∵平面ABCD∩平面PBC=BC,∴CM,CN,CB重合,故BC⊥AB,
∵四边形ABCD是菱形,∴BC与AB不一定垂直,故C错误;
对于D,∵四边形ABCD是菱形,∴BD⊥AC,
∵PA⊥平面ABCD,BD 平面ABCD,∴BD⊥PA,
∵PA∩AC=A,∴BD⊥平面PAC,∵BD 平面PBD,
∴平面PBD⊥平面PAC,故D正确.
故选D.
8.解析 (1)证明:在长方体ABCD-A1B1C1D1中,D1C1⊥平面BCC1B1.
∵B1C 平面BCC1B1,∴D1C1⊥B1C,
∵BC=CC1=1,∴四边形BCC1B1为正方形,
∴B1C⊥BC1.
又BC1∩D1C1=C1,BC1,D1C1 平面BD1C1,
∴B1C⊥平面BD1C1.
∵B1C 平面A1B1CD,
∴平面BD1C1⊥平面A1B1CD.
(2)假设在棱AB上存在点M,使D1B⊥平面MB1C.
连接BD交MC于点O(图略).
∵CM 平面MB1C,∴D1B⊥CM.
在长方体ABCD-A1B1C1D1中,D1D⊥平面ABCD.
∵CM 平面ABCD,∴D1D⊥CM.
又D1D∩D1B=D1,D1D,D1B 平面BDD1,∴CM⊥平面BDD1.
∵BD 平面BDD1,∴CM⊥BD.
∵四边形ABCD为矩形,∴△ABD∽△BCM,
∴=,设AM=m(0∴在棱AB上存在点M,使D1B⊥平面MB1C,此时AM=.
9.B 如图,过点A作AE⊥BD,交BD于点E,
∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AE 平面ABD,∴AE⊥平面BCD,
又∵BC 平面BCD,∴AE⊥BC.
∵DA⊥平面ABC,BC 平面ABC,
∴DA⊥BC,
又∵AE∩DA=A,AE,DA 平面ABD,
∴BC⊥平面ABD,又AB 平面ABD,
∴AB⊥BC,即△ABC为直角三角形,故选B.
10.B 连接AC1,∵∠BAC=90°,∴AC⊥AB,
∵BC1⊥AC,BC1∩AB=B,∴AC⊥平面ABC1,
又AC 平面ABC,∴平面ABC⊥平面ABC1,由面面垂直的性质知,由平面ABC1内一点C1向平面ABC作垂线,垂足必落在交线AB上.
11.证明 如题图(1),在梯形ABCD中,AD=CD=2,∠ADC=90°,过C作CE⊥AB,垂足为E,
∴四边形AECD为正方形,∴CE=AE=EB=2,
∴∠ACE=∠BCE=45°,
∴∠ACB=90°,即BC⊥AC,
如题图(2),平面ADC⊥平面ABC,且平面ADC∩平面ABC=AC,
又BC 平面ABC,且BC⊥AC,
∴BC⊥平面ADC.
12.解析 (1)证明:在△DCH中,∠ACD=60°,CH=2,CD=4,
由余弦定理得DH2=CD2+CH2-2CD·CH·cos∠ACD=12,则CD2=CH2+DH2,
即DH⊥AC,又平面ACFD⊥平面ABC,平面ACFD∩平面ABC=AC,DH 平面ACFD,所以DH⊥平面ABC,
又BC 平面ABC,所以DH⊥BC,
又BH⊥BC,BH∩DH=H,BH,DH 平面BDH,
所以BC⊥平面BDH,又DB 平面BDH,所以BC⊥DB,又BC∥EF,所以EF⊥DB.
(2)在Rt△BHC中,CH=2,BC=,BH⊥BC,则BH==1,∠ACB=30°,
由S△ABC=×AC×BC×sin 30°=,解得AC=3,由AC=3=AH+HC,得AH=1,
因此VD-ABH=S△ABH·DH=××12××2=,
所以三棱锥D-ABH的体积是.
能力提升练
1.B 如图所示,以CD,BD为邻边作平行四边形CDBE,连接AE,
因为BD⊥CD,CE∥BD,所以CE⊥CD,
又因为AC⊥CD,AC α,CE β,
所以二面角α-l-β的平面角为∠ACE,即∠ACE=,
因为四边形CDBE为平行四边形,
所以CE=BD=2,BE=CD=2,
所以在△ACE中,AE2=AC2+CE2-2AC·CEcos=1+4-2×1×2×=3,所以AE=,
因为BE∥CD,所以BE⊥CE,BE⊥AC,
又AC∩CE=C,AC,CE 平面ACE,
所以BE⊥平面ACE,
因为AE 平面ACE,所以BE⊥AE,
所以AB==.
因为BE∥CD,所以直线AB与CD所成的角相当于直线AB与BE所成的角,即为∠ABE,
所以cos∠ABE==,
故选B.
2.ABC 在正方形ABCD中,连接BD交AC于点O,则OA=OB=OC=OD=AC=2,且AC⊥BD,
在四面体ABCD中,AC⊥OB且AC⊥OD,又OB∩OD=O,OB,OD 平面OBD,
∴AC⊥平面OBD,又BD 平面OBD,∴AC⊥BD,故A是真命题;
因为AC⊥OB且AC⊥OD,所以∠BOD即为二面角D-AC-B的平面角,
当二面角D-AC-B为120°时,∠BOD=120°,
在△BOD中,由余弦定理得BD2=OD2+OB2-2OD·OBcos∠BOD=(2)2+(2)2-2×2×2×=24,故BD=2,故B是真命题;
当二面角D-AC-B为90°时,∠BOD=90°,
所以BD===4,
又CD=BC=4,所以△BCD是等边三角形,故C是真命题;
因为OA=OB=OC=OD=2,所以四面体ABCD外接球的球心是O,半径为2,
∴四面体ABCD的外接球的体积V=π×(2)3=,故D是假命题.
故选ABC.
3.答案
解析 由题意得∠A1C1B1=90°,则B1C1⊥A1C1,在直三棱柱ABC-A1B1C1中,CC1⊥平面A1B1C1,又B1C1 平面A1B1C1,所以B1C1⊥CC1,又CC1∩A1C1=C1,CC1,A1C1 平面ACC1A1,所以B1C1⊥平面ACC1A1,因为CD 平面ACC1A1,所以CD⊥B1C1,由条件可得△ACD,△DA1C1均为等腰直角三角形,则∠ADC=∠A1DC1=45°,所以∠C1DC=90°,即C1D⊥CD,由C1D∩B1C1=C1,C1D,B1C1 平面B1C1D,得CD⊥平面C1B1D,又DB1 平面C1B1D,所以CD⊥DB1,所以∠C1DB1为平面B1DC与平面DCC1所成的角.在Rt△C1B1D中,C1B1=2,C1D=2,所以tan∠C1DB1===.
4.解析 (1)证明:在△ABD中,AB=a,AD=2a,A=60°,
由余弦定理得BD==a,
所以AB2+BD2=AD2,所以∠ABD=90°,即AB⊥BD.
又因为二面角A-BD-C是直二面角,且平面ABD∩平面BCD=BD,AB 平面ABD,所以AB⊥平面BCD.
又CD 平面BCD,所以AB⊥CD.
(2)在△BCD中,E是BC的中点,由(1)易知∠BED=120°,BE=a.
过点B作BF⊥DE,交DE的延长线于点F,连接AF.
因为AB⊥平面BCD,DF 平面BCD,
所以DF⊥AB,
又DF⊥BF,AB∩BF=B,AB,BF 平面ABF,所以DF⊥平面ABF,
又AF 平面ABF,所以AF⊥DF,
所以∠AFB为二面角A-ED-B的平面角.
在Rt△BFE中,∠BEF=60°,BE=a,
因此BF=,
所以tan∠AFB===,
所以cos∠AFB=.
所以二面角A-ED-B的余弦值是.
5.ABC A中,连接AC,取AC的中点O,BE的中点M,连接MO,MF,易证明四边形AOMF是平行四边形,所以AC∥FM,又FM 平面BEF,AC 平面BEF,所以AC∥平面BEF,所以A正确;
B中,设B,C,E,F四点共面,因为BC∥AD,AD 平面ADEF,BC 平面ADEF,所以BC∥平面ADEF,又平面ADEF∩平面BCEF=EF,所以BC∥EF,所以AD∥EF,这与已知相矛盾,故B,C,E,F四点不可能共面,所以B正确;
C中,连接CF,DF,在梯形ADEF中,易得EF⊥FD,又EF⊥CF,FD∩CF=F,FD,CF 平面CDF,所以EF⊥平面CDF,又CD 平面CDF,所以CD⊥EF,显然CD⊥AD,EF与AD必相交,所以CD⊥平面ADEF,又CD 平面ABCD,所以平面ADEF⊥平面ABCD,所以C正确;
D中,延长AF至点G,使得AF=FG,连接BG,EG,易得平面BCE⊥平面ABF,过F作FN⊥BG于点N,则FN⊥平面BCE,若平面BCE⊥平面BEF,则过F作直线与平面BCE垂直,其垂足在BE上,前后矛盾,故D错误.故选ABC.
6.答案 DM⊥PC(或BM⊥PC)
解析 连接AC,由题意得BD⊥AC,
∵PA⊥底面ABCD,∴PA⊥BD.
又PA∩AC=A,PA,AC 平面PAC,
∴BD⊥平面PAC,∴BD⊥PC.
∴当DM⊥PC(或BM⊥PC)时,PC⊥平面MBD,
而PC 平面PCD,
∴平面MBD⊥平面PCD.
7.答案 ①③④
解析 对于①,由正方体的性质,得A1D1⊥平面AA1P,又A1D1 平面D1A1P,所以平面AA1P⊥平面D1A1P,故①正确;
对于②,当P是A1B的中点时,易得AP=,AD1=,D1P===,
满足AP2+D1P2=A,此时∠APD1是直角,故②错误;
对于③,连接D1C,DC1,如图所示:
由正方体的性质,得DC1⊥D1C,且BC⊥平面DCC1D1,DC1 平面DCC1D1,所以BC⊥DC1,
又D1C∩BC=C,D1C,BC 平面A1BCD1,
所以DC1⊥平面A1BCD1,
又D1P 平面A1BCD1,所以DC1⊥D1P,故③正确;
对于④,因为=,△B1D1C的面积是定值,
易知A1B∥平面B1D1C,所以点P到平面B1D1C的距离是定值,
所以三棱锥B1-D1PC的体积为定值,故④正确.
故答案为①③④.
8.解析 (1)证明:因为AB⊥平面BCD,CD 平面BCD,所以AB⊥CD.
因为CD⊥BC,AB∩BC=B,AB,BC 平面ABC,
所以CD⊥平面ABC.
又==λ(0<λ<1),
所以EF∥CD,所以EF⊥平面ABC,又EF 平面BEF,所以无论λ为何值,总有平面BEF⊥平面ABC.
(2)由(1)知EF⊥BE,又平面BEF⊥平面ACD,平面BEF∩平面ACD=EF,BE 平面BEF,
所以BE⊥平面ACD,所以BE⊥AC.
因为AB⊥平面BCD,BD,BC 平面BCD,
所以AB⊥BD,AB⊥BC,
因为BC=CD=1,∠BCD=90°,
所以BD=,
又∠ADB=60°,所以AB=×tan 60°=,
所以AC==,
由△ABC∽△AEB,得AB2=AE·AC,解得AE=,
所以λ==.
故当λ=时,平面BEF⊥平面ACD.
9.D 取CD的中点F,连接EF,FN,取FD的中点H,连接MH,HB,
又△ECD为正三角形,所以EF⊥CD,
因为M,H分别为ED,FD的中点,
所以MH∥EF,故MH⊥CD,
又平面ECD⊥平面ABCD,平面ECD∩平面ABCD=CD,EF,MN 平面ECD,
所以EF⊥平面ABCD,MH⊥平面ABCD,
又FN 平面ABCD,HB 平面ABCD,
所以EF⊥FN,MH⊥HB,
设AB=a,则EF=2MH=a,FN=a,BH=a,
则BM==a,EN==a,
则BM≠EN,故A中命题错误.
假设CD⊥MN,
又MH⊥CD,MH∩MN=M,MH,MN 平面MNH,
所以CD⊥平面MNH,又NH 平面MNH,
所以CD⊥NH,这与CD⊥NF矛盾,故假设不成立,CD,MN不互相垂直,故B中命题错误.
连接AN,易知直线AN 平面ABCD,
假设A,M,N三点共线,则M∈AN,
则M∈平面ABCD,这与M 平面ABCD矛盾,故假设不成立,故C中命题错误.
连接BD,由DM=ME,DN=NB,可得MN∥BE,MN=BE,
则四边形MNBE为梯形,则直线BM与EN相交,故D中命题正确.
故选D.
10.BC 对于A,因为底面ABCD是正方形,所以AB≠DB,因为AB=PB,所以PB=BD不成立,故A错误;
对于B,设底面正方形ABCD的中心为O,则P在以O为球心,OA为半径的球面上时符合题意,故B正确;
对于C,当平面PBC⊥底面ABCD时,
由面面垂直的性质可知AB⊥平面PBC,DC⊥平面PBC,显然符合题意,故C正确;
对于D,先证当两相交平面同时垂直于第三平面时,交线垂直于第三平面,
如图有
取A∈γ,作AB⊥a,AC⊥b,垂足分别为B,C,
由面面垂直的性质定理可知AB⊥α,AC⊥β,
又l α,l β,∴
又AB∩AC=A,AB,AC γ,所以由线面垂直的判定定理可知l⊥γ,
若“平面PAB⊥平面PBD”与“平面PCD⊥平面PBD”同时成立,
设平面PAB∩平面PCD=l,则P∈l,则l⊥平面PBD,
易知AB∥CD,AB 平面PCD,CD 平面PCD,所以AB∥平面PCD,则l∥AB,则有AB⊥平面PBD,又BD 平面PBD,所以AB⊥BD,显然AB⊥BD不成立,故D错误.故选BC.
11.解析 (1)证明:因为EA=EB,D为AB的中点,所以DE⊥AB,
因为平面ABE⊥平面ABC,平面ABE∩平面ABC=AB,DE 平面ABE,
所以DE⊥平面ABC.
因为BC=CF=2,FB=2,所以BC2+CF2=FB2,
所以CF⊥BC,同理CF⊥AC,
因为AC∩BC=C,AC,BC 平面ABC,
所以CF⊥平面ABC,所以DE∥CF.
(2)连接CD,FD,由(1)得DE∥平面BCF,则E到平面BCF的距离等于D到平面BCF的距离,所以VC-BEF=VE-BCF=VD-BCF,
过点D作DM⊥BC,垂足为M,
因为CF⊥平面ABC,DM 平面ABC,所以CF⊥DM,
又BC∩CF=C,BC,CF 平面BCF,所以DM⊥平面BCF,
又DM=BDsin∠DBC=1×=,
所以VD-BCF=×S△BCF×DM=××2×2×=,所以VC-BEF=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第四册
第十一章 立体几何初步
11.4 空间中的垂直关系
11.4.2 平面与平面垂直
基础过关练
题组一 二面角
1.(2023黑龙江牡丹江期末)从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角的关系是( )
A.互为余角 B.相等 C.其和为周角 D.互为补角
2.(2024湖北武汉部分重点中学期中)在四面体ABCD中,已知△ABD为等边三角形,△ABC为等腰直角三角形,斜边AB=4,CD=2,则二面角C-AB-D的大小为( )
A. B. C. D.
3.(2023北京朝阳期末)如图,正方体ABCD-A1B1C1D1的棱长为2,则二面角A1-BD-A的正弦值为 .
4.(2022山东威海期末)已知正方形ABCD的边长为2,E,F分别是边AB,CD的中点,沿EF将四边形AEFD折起,使二面角A-EF-B的大小为60°,则A,C两点间的距离为 .
题组二 平面与平面垂直的判定
5.(2024江西南昌第二中学期末)已知α,β是空间两个不同的平
面,m,n是空间两条不同的直线,则下列说法正确的是( )
A.若m∥α,n∥β,且m∥n,则α∥β
B.若m∥α,n∥β,且m⊥n,则α⊥β
C.若m⊥α,n∥β,且m⊥n,则α⊥β
D.若m⊥α,n⊥β,且m⊥n,则α⊥β
6.(2024上海格致中学期中)给出下列命题,其中是假命题是( )
A.存在每个面都是直角三角形的四面体
B.若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直
C.在四棱柱中,若过相对侧棱的两个截面都垂直于底面,则该四棱柱为直四棱柱
D.棱柱的侧棱都相等,侧面都是全等的平行四边形
7.(2024四川内江铁路中学期中)在四棱锥P-ABCD中,四边形ABCD为菱形,PA⊥平面ABCD,E是PD的中点,下列叙述正确的是( )
A.CE∥平面PAB
B.CE⊥平面PAD
C.平面PBC⊥平面PAB
D.平面PBD⊥平面PAC
8.(2022江西新余期末)如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1.
(1)求证:平面BD1C1⊥平面A1B1CD;
(2)在棱AB上是否存在一点M(不含端点),使D1B⊥平面MB1C 若存在,请确定点M的位置;若不存在,请说明理由.
题组三 平面与平面垂直的性质
9.在四面体ABCD中,平面ABD⊥平面BCD,且DA⊥平面ABC,则△ABC的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
10.(2022黑龙江鹤岗一中期末)如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( )
A.直线AC上 B.直线AB上
C.直线BC上 D.△ABC内部
11.(2023山西忻州期末)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到三棱锥D-ABC(如图2).求证:BC⊥平面ADC.
图1 图2
12.(2024四川成都三诊)如图,在三棱台ABC-DEF中,H在AC边上,平面ACFD⊥平面ABC,∠ACD=60°,CH=2,CD=4,BC=,BH⊥BC.
(1)证明:EF⊥BD;
(2)若△ABC的面积为,求三棱锥D-ABH的体积.
能力提升练
题组一 二面角
1.(2023湖北黄冈期末)已知在大小为的二面角α-l-β中,A∈α,B∈β,AC⊥l于点C,BD⊥l于点D,且CD=BD=2AC=2,则直线AB与CD所成角的余弦值为( )
A. B.
C. D.
2.(多选题)(2024贵州遵义第四中学一模)将边长为4的正方形ABCD沿对角线AC折起,使点D不在平面ABC内,则下列命题是真命题的是 ( )
A.不论二面角D-AC-B为何值,总有AC⊥BD
B.当二面角D-AC-B为120°时,BD=2
C.当二面角D-AC-B为90°时,△BCD是等边三角形
D.不论二面角D-AC-B为何值,四面体ABCD外接球的体积都为
3.(2022浙江学军中学期末)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,D为AA1的中点,则平面B1DC与平面DCC1所成角的正切值为 .
4.(2022湖南益阳期末)在平行四边形ABCD中,AB=CD=a,AD=2a,E是BC的中点,A=60°,现将该平行四边形沿对角线BD折成直二面角A-BD-C.
(1)求证:AB⊥CD;
(2)求二面角A-ED-B的余弦值.
题组二 平面与平面垂直的判定
5.(多选题)在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图①).将四边形ADEF沿AD折起,连接BE,BF,CE(如图②).在折起的过程中,下列说法正确的是( )
A.AC∥平面BEF B.B,C,E,F四点不可能共面
C.若EF⊥CF,则平面ADEF⊥平面ABCD
D.平面BCE与平面BEF可能垂直
6.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一个动点,当点M满足 时,平面MBD⊥平面PCD.(填写一个你认为正确的条件即可)
7.(2023北京师范大学附属实验中学月考)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P是线段A1B上一动点(不与A1,B重合),则下列结论中:
①平面AA1P⊥平面D1A1P;②∠APD1一定是锐角;
③DC1⊥D1P;④三棱锥B1-D1PC的体积为定值.
其中结论正确的是 .(填序号)
8.(2023江西南昌期中)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且==λ(0<λ<1).
(1)求证:无论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD
题组三 平面与平面垂直的性质
9.(2024上海金山二模)如图,在四棱锥E-ABCD中,点N为正方形
ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则以下命题中正确的是( )
A.BM=EN B.CD⊥MN
C.A,M,N三点共线 D.直线BM与EN相交
10.(多选题)(2024山东聊城二模)已知四棱锥P-ABCD的底面ABCD是正方形,则下列关系能同时成立的是( )
A.“AB=PB”与“PB=BD”
B.“PA⊥PC”与“PB⊥PD”
C.“PB⊥CD”与“PC⊥AB”
D.“平面PAB⊥平面PBD”与“平面PCD⊥平面PBD”
11.(2022江西南昌八一中学等名校期末)如图,平面ABE⊥平面ABC,△ABC是等边三角形,D为AB的中点,BC=CF=2,FA=FB=2,EA=EB.
(1)证明:DE∥CF;
(2)求三棱锥C-BEF的体积.
答案与分层梯度式解析
基础过关练
1.D 如图,A为二面角α-l-β内任意一点,AB⊥α,AC⊥β,过B作BD⊥l于D,
连接CD,因为AB⊥α,l α,所以AB⊥l,
因为AC⊥β,l β,所以AC⊥l,且AB∩AC=A,
所以l⊥平面ABCD,且CD 平面ABCD,所以l⊥CD,
则∠BDC为二面角α-l-β的平面角,
又∠ABD=∠ACD=90°,∠BAC为两条垂线AB与AC所成的角,所以∠A+∠BDC=180°,
所以两条垂线所夹的角与二面角的平面角互为补角.
故选D.
2.A 取AB的中点O,连接CO,DO,如图,
由AD=BD=AB=4,AC=BC,∠ACB=90°,得OC⊥AB,OD⊥AB,
因此∠COD是二面角C-AB-D的平面角,
在△COD中,OC=2,OD=2,CD=2,
由余弦定理得cos∠COD===-,
又0≤∠COD≤π,
所以∠COD=,
所以二面角C-AB-D的大小为.故选A.
3.答案
解析 如图,连接AC交BD于点O,连接A1O,
在正方体ABCD-A1B1C1D1中,O为BD的中点,所以AO⊥BD,又A1D=A1B,所以A1O⊥BD,所以∠A1OA即为二面角A1-BD-A的平面角,
又AO=AC==,AA1=2,
所以A1O==,
所以sin∠A1OA===,
即二面角A1-BD-A的正弦值为.
4.答案
解析 如图,连接AB,AC,取BE的中点G,连接AG,CG,由题意得EF⊥AE,EF⊥BE,所以∠AEB是二面角A-EF-B的平面角,则∠AEB=60°,又AE=BE=1,所以△ABE是正三角形,于是AG⊥BE,AG=.
根据EF⊥AE,EF⊥BE,AE∩BE=E,可得EF⊥平面ABE,又AG 平面ABE,所以EF⊥AG,又AG⊥BE,BE∩EF=E,所以AG⊥平面BCFE,又GC 平面BCFE,所以AG⊥GC,又GC2=BC2+BG2=,
所以AC===.
5.D 对于A,若m∥α,n∥β,且m∥n,则α,β可能相交或平行,故A错误;
对于B,若m∥α,n∥β,且m⊥n,则α,β可能相交或平行,故B错误;
对于C,若m⊥α,n∥β,且m⊥n,则α,β可能相交或平行,故C错误;
对于D,若m⊥α,m⊥n,则n在平面α内或n∥α,又n⊥β,所以α⊥β,故D正确.
故选D.
6.D 对于A,如图,在正方体ABCD-A1B1C1D1中,
三棱锥C1-ABC的四个面均为直角三角形,故A是真命题.
对于B,如图,在三棱锥P-ABC中,CA⊥CP,CA⊥CB,CP⊥CB,
因为CA⊥CP,CA⊥CB,且CP∩CB=C,CP,CB 平面PBC,所以CA⊥平面PBC,
又CA 平面PAC,所以平面PAC⊥平面PBC.
同理可得,平面PAC⊥平面ABC,平面ABC⊥平面PBC,故B是真命题.
对于C,如图,平面ACC1A1⊥平面ABCD,平面BDD1B1⊥平面ABCD,平面ACC1A1∩平面BDD1B1=OO1,
所以OO1⊥平面ABCD,易知OO1∥AA1,则AA1⊥平面ABCD,故C是真命题.
对于D,根据棱柱的定义可得,棱柱的侧棱都相等,侧面都是平行四边形,但是不一定全等,故D是假命题.
故选D.
7.D 对于A,∵四边形ABCD是菱形,
∴CD∥AB,
∵CD 平面PAB,AB 平面PAB,
∴CD∥平面PAB,假设CE∥平面PAB,
∵CE∩CD=C,CE,CD 平面PCD,
∴平面PCD∥平面PAB,显然不成立,故假设不成立,故A错误;
对于B,过点C作CF⊥AD,垂足为点F,
∵PA⊥平面ABCD,CF 平面ABCD,
∴CF⊥PA,∵CF⊥AD,PA∩AD=A,PA,AD 平面PAD,
∴CF⊥平面PAD,
∵过C作平面PAD的垂线有且只有一条,
∴CE与平面PAD不垂直,故B错误;
对于C,过点C作CM⊥AB,垂足为点M,
∵PA⊥平面ABCD,CM 平面ABCD,∴CM⊥PA,
∵CM⊥AB,PA∩AB=A,PA,AB 平面PAB,∴CM⊥平面PAB,
若平面PBC⊥平面PAB,过点C作CN⊥PB,垂足为N,
∵平面PBC⊥平面PAB,平面PBC∩平面PAB=PB,CN 平面PBC,∴CN⊥平面PAB,
∵过点C作平面PAB的垂线有且只有一条,
∴CM,CN重合,
∵平面ABCD∩平面PBC=BC,∴CM,CN,CB重合,故BC⊥AB,
∵四边形ABCD是菱形,∴BC与AB不一定垂直,故C错误;
对于D,∵四边形ABCD是菱形,∴BD⊥AC,
∵PA⊥平面ABCD,BD 平面ABCD,∴BD⊥PA,
∵PA∩AC=A,∴BD⊥平面PAC,∵BD 平面PBD,
∴平面PBD⊥平面PAC,故D正确.
故选D.
8.解析 (1)证明:在长方体ABCD-A1B1C1D1中,D1C1⊥平面BCC1B1.
∵B1C 平面BCC1B1,∴D1C1⊥B1C,
∵BC=CC1=1,∴四边形BCC1B1为正方形,
∴B1C⊥BC1.
又BC1∩D1C1=C1,BC1,D1C1 平面BD1C1,
∴B1C⊥平面BD1C1.
∵B1C 平面A1B1CD,
∴平面BD1C1⊥平面A1B1CD.
(2)假设在棱AB上存在点M,使D1B⊥平面MB1C.
连接BD交MC于点O(图略).
∵CM 平面MB1C,∴D1B⊥CM.
在长方体ABCD-A1B1C1D1中,D1D⊥平面ABCD.
∵CM 平面ABCD,∴D1D⊥CM.
又D1D∩D1B=D1,D1D,D1B 平面BDD1,∴CM⊥平面BDD1.
∵BD 平面BDD1,∴CM⊥BD.
∵四边形ABCD为矩形,∴△ABD∽△BCM,
∴=,设AM=m(0
9.B 如图,过点A作AE⊥BD,交BD于点E,
∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AE 平面ABD,∴AE⊥平面BCD,
又∵BC 平面BCD,∴AE⊥BC.
∵DA⊥平面ABC,BC 平面ABC,
∴DA⊥BC,
又∵AE∩DA=A,AE,DA 平面ABD,
∴BC⊥平面ABD,又AB 平面ABD,
∴AB⊥BC,即△ABC为直角三角形,故选B.
10.B 连接AC1,∵∠BAC=90°,∴AC⊥AB,
∵BC1⊥AC,BC1∩AB=B,∴AC⊥平面ABC1,
又AC 平面ABC,∴平面ABC⊥平面ABC1,由面面垂直的性质知,由平面ABC1内一点C1向平面ABC作垂线,垂足必落在交线AB上.
11.证明 如题图(1),在梯形ABCD中,AD=CD=2,∠ADC=90°,过C作CE⊥AB,垂足为E,
∴四边形AECD为正方形,∴CE=AE=EB=2,
∴∠ACE=∠BCE=45°,
∴∠ACB=90°,即BC⊥AC,
如题图(2),平面ADC⊥平面ABC,且平面ADC∩平面ABC=AC,
又BC 平面ABC,且BC⊥AC,
∴BC⊥平面ADC.
12.解析 (1)证明:在△DCH中,∠ACD=60°,CH=2,CD=4,
由余弦定理得DH2=CD2+CH2-2CD·CH·cos∠ACD=12,则CD2=CH2+DH2,
即DH⊥AC,又平面ACFD⊥平面ABC,平面ACFD∩平面ABC=AC,DH 平面ACFD,所以DH⊥平面ABC,
又BC 平面ABC,所以DH⊥BC,
又BH⊥BC,BH∩DH=H,BH,DH 平面BDH,
所以BC⊥平面BDH,又DB 平面BDH,所以BC⊥DB,又BC∥EF,所以EF⊥DB.
(2)在Rt△BHC中,CH=2,BC=,BH⊥BC,则BH==1,∠ACB=30°,
由S△ABC=×AC×BC×sin 30°=,解得AC=3,由AC=3=AH+HC,得AH=1,
因此VD-ABH=S△ABH·DH=××12××2=,
所以三棱锥D-ABH的体积是.
能力提升练
1.B 如图所示,以CD,BD为邻边作平行四边形CDBE,连接AE,
因为BD⊥CD,CE∥BD,所以CE⊥CD,
又因为AC⊥CD,AC α,CE β,
所以二面角α-l-β的平面角为∠ACE,即∠ACE=,
因为四边形CDBE为平行四边形,
所以CE=BD=2,BE=CD=2,
所以在△ACE中,AE2=AC2+CE2-2AC·CEcos=1+4-2×1×2×=3,所以AE=,
因为BE∥CD,所以BE⊥CE,BE⊥AC,
又AC∩CE=C,AC,CE 平面ACE,
所以BE⊥平面ACE,
因为AE 平面ACE,所以BE⊥AE,
所以AB==.
因为BE∥CD,所以直线AB与CD所成的角相当于直线AB与BE所成的角,即为∠ABE,
所以cos∠ABE==,
故选B.
2.ABC 在正方形ABCD中,连接BD交AC于点O,则OA=OB=OC=OD=AC=2,且AC⊥BD,
在四面体ABCD中,AC⊥OB且AC⊥OD,又OB∩OD=O,OB,OD 平面OBD,
∴AC⊥平面OBD,又BD 平面OBD,∴AC⊥BD,故A是真命题;
因为AC⊥OB且AC⊥OD,所以∠BOD即为二面角D-AC-B的平面角,
当二面角D-AC-B为120°时,∠BOD=120°,
在△BOD中,由余弦定理得BD2=OD2+OB2-2OD·OBcos∠BOD=(2)2+(2)2-2×2×2×=24,故BD=2,故B是真命题;
当二面角D-AC-B为90°时,∠BOD=90°,
所以BD===4,
又CD=BC=4,所以△BCD是等边三角形,故C是真命题;
因为OA=OB=OC=OD=2,所以四面体ABCD外接球的球心是O,半径为2,
∴四面体ABCD的外接球的体积V=π×(2)3=,故D是假命题.
故选ABC.
3.答案
解析 由题意得∠A1C1B1=90°,则B1C1⊥A1C1,在直三棱柱ABC-A1B1C1中,CC1⊥平面A1B1C1,又B1C1 平面A1B1C1,所以B1C1⊥CC1,又CC1∩A1C1=C1,CC1,A1C1 平面ACC1A1,所以B1C1⊥平面ACC1A1,因为CD 平面ACC1A1,所以CD⊥B1C1,由条件可得△ACD,△DA1C1均为等腰直角三角形,则∠ADC=∠A1DC1=45°,所以∠C1DC=90°,即C1D⊥CD,由C1D∩B1C1=C1,C1D,B1C1 平面B1C1D,得CD⊥平面C1B1D,又DB1 平面C1B1D,所以CD⊥DB1,所以∠C1DB1为平面B1DC与平面DCC1所成的角.在Rt△C1B1D中,C1B1=2,C1D=2,所以tan∠C1DB1===.
4.解析 (1)证明:在△ABD中,AB=a,AD=2a,A=60°,
由余弦定理得BD==a,
所以AB2+BD2=AD2,所以∠ABD=90°,即AB⊥BD.
又因为二面角A-BD-C是直二面角,且平面ABD∩平面BCD=BD,AB 平面ABD,所以AB⊥平面BCD.
又CD 平面BCD,所以AB⊥CD.
(2)在△BCD中,E是BC的中点,由(1)易知∠BED=120°,BE=a.
过点B作BF⊥DE,交DE的延长线于点F,连接AF.
因为AB⊥平面BCD,DF 平面BCD,
所以DF⊥AB,
又DF⊥BF,AB∩BF=B,AB,BF 平面ABF,所以DF⊥平面ABF,
又AF 平面ABF,所以AF⊥DF,
所以∠AFB为二面角A-ED-B的平面角.
在Rt△BFE中,∠BEF=60°,BE=a,
因此BF=,
所以tan∠AFB===,
所以cos∠AFB=.
所以二面角A-ED-B的余弦值是.
5.ABC A中,连接AC,取AC的中点O,BE的中点M,连接MO,MF,易证明四边形AOMF是平行四边形,所以AC∥FM,又FM 平面BEF,AC 平面BEF,所以AC∥平面BEF,所以A正确;
B中,设B,C,E,F四点共面,因为BC∥AD,AD 平面ADEF,BC 平面ADEF,所以BC∥平面ADEF,又平面ADEF∩平面BCEF=EF,所以BC∥EF,所以AD∥EF,这与已知相矛盾,故B,C,E,F四点不可能共面,所以B正确;
C中,连接CF,DF,在梯形ADEF中,易得EF⊥FD,又EF⊥CF,FD∩CF=F,FD,CF 平面CDF,所以EF⊥平面CDF,又CD 平面CDF,所以CD⊥EF,显然CD⊥AD,EF与AD必相交,所以CD⊥平面ADEF,又CD 平面ABCD,所以平面ADEF⊥平面ABCD,所以C正确;
D中,延长AF至点G,使得AF=FG,连接BG,EG,易得平面BCE⊥平面ABF,过F作FN⊥BG于点N,则FN⊥平面BCE,若平面BCE⊥平面BEF,则过F作直线与平面BCE垂直,其垂足在BE上,前后矛盾,故D错误.故选ABC.
6.答案 DM⊥PC(或BM⊥PC)
解析 连接AC,由题意得BD⊥AC,
∵PA⊥底面ABCD,∴PA⊥BD.
又PA∩AC=A,PA,AC 平面PAC,
∴BD⊥平面PAC,∴BD⊥PC.
∴当DM⊥PC(或BM⊥PC)时,PC⊥平面MBD,
而PC 平面PCD,
∴平面MBD⊥平面PCD.
7.答案 ①③④
解析 对于①,由正方体的性质,得A1D1⊥平面AA1P,又A1D1 平面D1A1P,所以平面AA1P⊥平面D1A1P,故①正确;
对于②,当P是A1B的中点时,易得AP=,AD1=,D1P===,
满足AP2+D1P2=A,此时∠APD1是直角,故②错误;
对于③,连接D1C,DC1,如图所示:
由正方体的性质,得DC1⊥D1C,且BC⊥平面DCC1D1,DC1 平面DCC1D1,所以BC⊥DC1,
又D1C∩BC=C,D1C,BC 平面A1BCD1,
所以DC1⊥平面A1BCD1,
又D1P 平面A1BCD1,所以DC1⊥D1P,故③正确;
对于④,因为=,△B1D1C的面积是定值,
易知A1B∥平面B1D1C,所以点P到平面B1D1C的距离是定值,
所以三棱锥B1-D1PC的体积为定值,故④正确.
故答案为①③④.
8.解析 (1)证明:因为AB⊥平面BCD,CD 平面BCD,所以AB⊥CD.
因为CD⊥BC,AB∩BC=B,AB,BC 平面ABC,
所以CD⊥平面ABC.
又==λ(0<λ<1),
所以EF∥CD,所以EF⊥平面ABC,又EF 平面BEF,所以无论λ为何值,总有平面BEF⊥平面ABC.
(2)由(1)知EF⊥BE,又平面BEF⊥平面ACD,平面BEF∩平面ACD=EF,BE 平面BEF,
所以BE⊥平面ACD,所以BE⊥AC.
因为AB⊥平面BCD,BD,BC 平面BCD,
所以AB⊥BD,AB⊥BC,
因为BC=CD=1,∠BCD=90°,
所以BD=,
又∠ADB=60°,所以AB=×tan 60°=,
所以AC==,
由△ABC∽△AEB,得AB2=AE·AC,解得AE=,
所以λ==.
故当λ=时,平面BEF⊥平面ACD.
9.D 取CD的中点F,连接EF,FN,取FD的中点H,连接MH,HB,
又△ECD为正三角形,所以EF⊥CD,
因为M,H分别为ED,FD的中点,
所以MH∥EF,故MH⊥CD,
又平面ECD⊥平面ABCD,平面ECD∩平面ABCD=CD,EF,MN 平面ECD,
所以EF⊥平面ABCD,MH⊥平面ABCD,
又FN 平面ABCD,HB 平面ABCD,
所以EF⊥FN,MH⊥HB,
设AB=a,则EF=2MH=a,FN=a,BH=a,
则BM==a,EN==a,
则BM≠EN,故A中命题错误.
假设CD⊥MN,
又MH⊥CD,MH∩MN=M,MH,MN 平面MNH,
所以CD⊥平面MNH,又NH 平面MNH,
所以CD⊥NH,这与CD⊥NF矛盾,故假设不成立,CD,MN不互相垂直,故B中命题错误.
连接AN,易知直线AN 平面ABCD,
假设A,M,N三点共线,则M∈AN,
则M∈平面ABCD,这与M 平面ABCD矛盾,故假设不成立,故C中命题错误.
连接BD,由DM=ME,DN=NB,可得MN∥BE,MN=BE,
则四边形MNBE为梯形,则直线BM与EN相交,故D中命题正确.
故选D.
10.BC 对于A,因为底面ABCD是正方形,所以AB≠DB,因为AB=PB,所以PB=BD不成立,故A错误;
对于B,设底面正方形ABCD的中心为O,则P在以O为球心,OA为半径的球面上时符合题意,故B正确;
对于C,当平面PBC⊥底面ABCD时,
由面面垂直的性质可知AB⊥平面PBC,DC⊥平面PBC,显然符合题意,故C正确;
对于D,先证当两相交平面同时垂直于第三平面时,交线垂直于第三平面,
如图有
取A∈γ,作AB⊥a,AC⊥b,垂足分别为B,C,
由面面垂直的性质定理可知AB⊥α,AC⊥β,
又l α,l β,∴
又AB∩AC=A,AB,AC γ,所以由线面垂直的判定定理可知l⊥γ,
若“平面PAB⊥平面PBD”与“平面PCD⊥平面PBD”同时成立,
设平面PAB∩平面PCD=l,则P∈l,则l⊥平面PBD,
易知AB∥CD,AB 平面PCD,CD 平面PCD,所以AB∥平面PCD,则l∥AB,则有AB⊥平面PBD,又BD 平面PBD,所以AB⊥BD,显然AB⊥BD不成立,故D错误.故选BC.
11.解析 (1)证明:因为EA=EB,D为AB的中点,所以DE⊥AB,
因为平面ABE⊥平面ABC,平面ABE∩平面ABC=AB,DE 平面ABE,
所以DE⊥平面ABC.
因为BC=CF=2,FB=2,所以BC2+CF2=FB2,
所以CF⊥BC,同理CF⊥AC,
因为AC∩BC=C,AC,BC 平面ABC,
所以CF⊥平面ABC,所以DE∥CF.
(2)连接CD,FD,由(1)得DE∥平面BCF,则E到平面BCF的距离等于D到平面BCF的距离,所以VC-BEF=VE-BCF=VD-BCF,
过点D作DM⊥BC,垂足为M,
因为CF⊥平面ABC,DM 平面ABC,所以CF⊥DM,
又BC∩CF=C,BC,CF 平面BCF,所以DM⊥平面BCF,
又DM=BDsin∠DBC=1×=,
所以VD-BCF=×S△BCF×DM=××2×2×=,所以VC-BEF=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
