2025人教B版高中数学必修第四册强化练习题(含解析)--第九章 解三角形
文档属性
| 名称 | 2025人教B版高中数学必修第四册强化练习题(含解析)--第九章 解三角形 |

|
|
| 格式 | docx | ||
| 文件大小 | 397.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第四册
第九章 解三角形
全卷满分150分 考试用时120分钟
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在△ABC中,内角A,B,C的对边分别为a,b,c,则下列等式中成立的是( )
A.asin B=bsin A B.c=
C. D.a+b-c=sin A+sin B-sin C
2.在△ABC中,角A,B,C的对边分别是a,b,c,且a=,bcos A=sin B,则A=( )
A.
3.我舰在岛A南偏西50°方向的B处,且A,B距离为12千米,发现敌舰正离开岛A沿北偏西10°的方向以每小时10千米的速度航行,若我舰要用2小时追上敌舰,则速度大小为( )
A.28千米/时 B.14千米/时
C.14千米/时 D.20千米/时
4.在△ABC中,AB=3,AD⊥AC,且AD交BC于点D,AD=3,则sin C=( )
A.
5.已知△ABC的内角A,B,C的对边分别为a,b,c,若cos C=,bcos A+acos B=2,则△ABC外接圆的面积为 ( )
A.4π B.8π C.9π D.36π
6.在△ABC中,内角A,B,C的对边分别为a,b,c,且A=,b=4,那么满足条件的三角形的个数为( )
A.0 B.1 C.2 D.无数
7.已知△ABC的内角A,B,C的对边分别为a,b,c,S表示三角形的面积,若asin A+bsin B=csin C,S=(a2+c2-b2),则△ABC的形状是( )
A.直角三角形 B.等腰三角形
C.等腰或直角三角形 D.等腰直角三角形
8.如图甲,首钢滑雪大跳台是冬奥历史上第一座与工业遗产再利用直接结合的竞赛场馆,大跳台的设计中融入了世界文化遗产敦煌壁画中“飞天”的元素.如图乙,某研究性学习小组为了估算赛道造型最高点A距离地面的高度AB(AB与地面垂直),在赛道一侧找到一座建筑物CD,测得CD的高度为h,并从C点测得A点的仰角为30°;在赛道与建筑物CD之间的地面上的点E处测得A点,C点的仰角分别为75°和30°(其中B,E,D三点共线).该学习小组利用这些数据得AB约为60米,则CD的高h约为( )
(参考数据:≈2.45)
A.11米 B.20.8米 C.25.4米 D.31.8米
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列命题中,正确的是( )
A.在△ABC中,A>B,则sin A>sin B
B.在锐角△ABC中,不等式sin A>cos B恒成立
C.在△ABC中,若acos A=bcos B,则△ABC必是等腰直角三角形
D.在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形
10.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=5,b=6,c=7,下列说法正确的是( )
A.sin A∶sin B∶sin C=5∶6∶7
B.cos A∶cos B∶cos C=5∶6∶7
C.△ABC是锐角三角形
D.△ABC的最大内角是最小内角的2倍
11.在△ABC中,角A,B,C的对边分别为a,b,c,如果a,b,c满足a≤(b+c),那么下列结论中正确的是( )
A.sin A≤(sin B+sin C)
B.△ABC不可能是直角三角形
C.角A一定是锐角
D.角A一定是钝角
三、填空题(本大题共3小题,每小题5分,共15分.将答案填在题中横线上)
12.已知△ABC中,AB=cos B=0,则△ABC的面积为 .
13.若a,a+1,a+2是钝角三角形的三边,则a的取值范围是 .
14.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知bcos C+ccos B=3acos A,若S为△ABC的面积,则当的值为 .
四、解答题(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知.
(1)求证:△ABC为等腰三角形;
(2)从条件①、条件②、条件③这三个条件中选择一个作为已知条件,使△ABC存在且唯一,求b的值.
条件①:B=;条件③:AB边上的高为3.
16.(15分)已知a,b,c分别是△ABC的内角A,B,C的对边,满足acsin A+4sin C=4csin A.
(1)求a的值;
(2)△ABC的外接圆为圆O(O在△ABC内部),S△OBC=,b+c=4,判断△ABC的形状,并说明理由.
17.(15分)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,bsin A+atan A·cos B=2asin C.
(1)求A;
(2)若D为BC延长线上一点,且∠CAD=的取值范围.
18.(17分)勒洛三角形是由19世纪德国工程师勒洛在研究机械分类时发现的.如图1,以等边三角形ABC的每个顶点为圆心、边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形就是勒洛三角形ABC.受此启发,某数学兴趣小组绘制了勒洛五边形.如图2,分别以正五边形ABCDE的各顶点为圆心,对角线长为半径,在距离该顶点较远的另外两个顶点间画一段圆弧,五段圆弧围成的曲边五边形就是勒洛五边形ABCDE.设正五边形ABCDE的边长为1.
(1)求勒洛五边形ABCDE的周长l1;
(2)设正五边形ABCDE的外接圆的周长为l2,试比较l1与l2的大小,并说明理由.
图1 图2
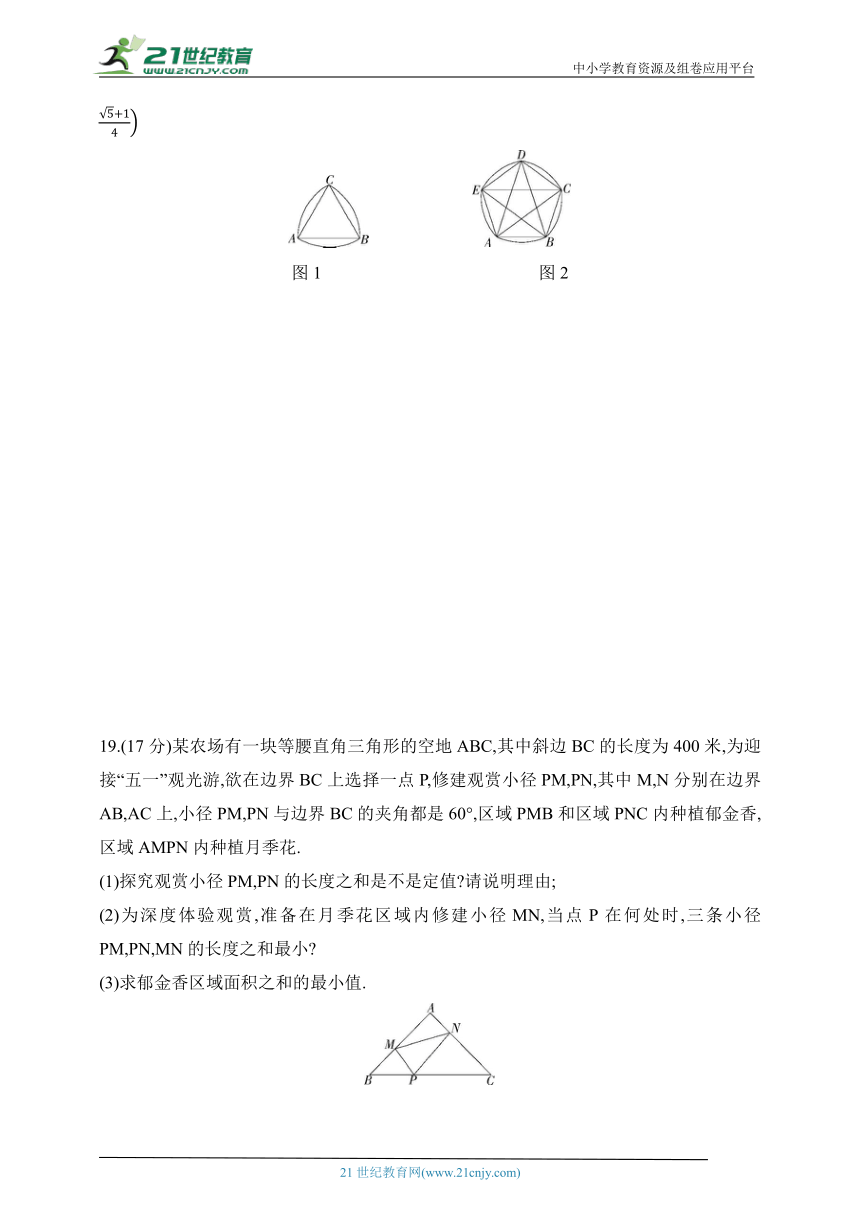
19.(17分)某农场有一块等腰直角三角形的空地ABC,其中斜边BC的长度为400米,为迎接“五一”观光游,欲在边界BC上选择一点P,修建观赏小径PM,PN,其中M,N分别在边界AB,AC上,小径PM,PN与边界BC的夹角都是60°,区域PMB和区域PNC内种植郁金香,区域AMPN内种植月季花.
(1)探究观赏小径PM,PN的长度之和是不是定值 请说明理由;
(2)为深度体验观赏,准备在月季花区域内修建小径MN,当点P在何处时,三条小径PM,PN,MN的长度之和最小
(3)求郁金香区域面积之和的最小值.
答案全解全析
1.A 由正弦定理可得,所以asin B=bsin A.
2.D 由bcos A=sin B得,
又a=,
又A∈(0,π),所以A=.故选D.
3.B 如图,设我舰在C处追上敌舰,速度大小为v,在△ABC中,AC=10×2=20(千米),AB=12(千米),∠BAC=120°,所以BC2=AB2+AC2-2AB·ACcos 120°=784,所以BC=28(千米),故v=14千米/时.
4.B 由cos∠BAC=-
=-cos∠BAC=,
又∠BAD为锐角,所以cos∠BAD=,
在△ABD中,由余弦定理得BD=,
所以sin C=cos∠ADC=-cos∠ADB=-
=-.故选B.
5.C 设△ABC外接圆的半径为R,由题意及余弦定理得b·=2,解得c=2,
由cos C==6,所以R=3,
所以△ABC外接圆的面积为πR2=9π.
6.C 在△ABC中,A=,b=4,由a2=b2+c2-2bccos A,可得
14=16+c2-4c,即c2-4c+2=0,解得c=2±,
所以满足条件的三角形的个数为2,故选C.
7.D 由asin A+bsin B=csin C得a2+b2=c2,所以△ABC是直角三角形.
又由三角形的面积公式得×2accos B,整理得tan B=1,因此B=45°,故△ABC是等腰直角三角形.
8.C 由题意知∠AEB=75°,∠CED=30°,则∠AEC=75°,∠ACE=60°,∠CAE=45°,在Rt△ABE中,AE=,
在△ACE中,,
则CE=,
∵sin 75°=sin(45°+30°)=,
∴CD=≈60-20×1.73=25.4(米),
∴CD的高h约为25.4米,故选C.
9.ABD 对于A,由A>B可得a>b,利用正弦定理可得sin A>sin B,故A正确;
对于B,在锐角△ABC中,A,B∈,
∵A+B>=cos B,故B正确;
对于C,在△ABC中,由acos A=bcos B及正弦定理可得sin Acos A=sin Bcos B,∴sin 2A=sin 2B,
∵A,B∈(0,π),∴2A=2B或2A=π-2B,∴A=B或A+B=,
∴△ABC是等腰三角形或直角三角形,故C错误;
对于D,B=60°,b2=ac,结合余弦定理可得ac=b2=a2+c2-ac,∴(a-c)2=0,解得a=c,所以A=C=B=60°,∴△ABC是等边三角形,故D正确.
故选ABD.
10.AC 对于A,由正弦定理可得sin A∶sin B∶sin C=a∶b∶c=5∶6∶7,A正确;
对于B,由余弦定理可得cos A=,
所以cos A∶cos B∶cos C=25∶19∶7,B错误;
对于C,因为a0,所以C为锐角,故△ABC为锐角三角形,C正确;
对于D,由题意知,A为最小角,则cos 2A=2cos2A-1=2×,所以2A∈(0,π),
所以C≠2A,D错误.
故选AC.
11.AC 由正弦定理结合已知条件易知A选项正确;
当△ABC是直角三角形且a是较短的直角边时,a≤(b+c)成立,故B选项错误;
将不等式两边平方得a2≤(当且仅当b=c时,第二个等号成立),因为A为三角形的内角,所以0°12.答案
解析 由sin B+.
13.答案 1解析 易知a结合题意可知a+2所对的角为钝角,
所以解得1所以a的取值范围是114.答案 +1
解析 由正弦定理及bcos C+ccos B=3acos A,
可得sin Bcos C+sin Ccos B=3sin Acos A,
所以sin(B+C)=sin A=3sin Acos A,
因为A∈(0,π),所以sin A≠0,
所以cos A=.
由余弦定理得a2=b2+c2-2bccos A=b2+c2-bc,
又S=,
当且仅当b=c时取“=”,
此时a2=b2+c2-c2,
所以a=+1.
15.解析 (1)证明:由a,
在△ABC中,由余弦定理可得a2=,(3分)
整理,得(a-c)(3a+5c)=0,故有a=c,
故△ABC为等腰三角形.(6分)
(2)选择条件①:B=.
由(1)知a=c,则有A=C=,
此时cos A=cos,
与已知矛盾,三角形无解,不可选.(8分)
选择条件②:△ABC的面积为.
因为cos A=.
由(1)知a=c,则有A=C,所以sin B=sin(π-2A)=sin 2A=2sin Acos A=2×,(11分)
又S△ABC=,所以a=c=5.
由正弦定理得.
三角形存在且唯一,可选.(13分)
选择条件③:AB边上的高为3.同条件②得sin B=,(11分)
因此a=.三角形存在且唯一,可选.(13分)
16.解析 (1)由正弦定理及acsin A+4sin C=4csin A得a2c+4c=4ac,
∵c≠0,∴a2+4=4a,∴(a-2)2=0,∴a=2.(4分)
(2)△ABC为等边三角形,理由如下:(5分)
记BC的中点为D,连接OD,易知OD⊥BC.
则S△OBC=,故∠BOC=120°,
故A=∠BOC=60°,(9分)
由余弦定理可知,a2=b2+c2-2bccos A,即4=b2+c2-bc,
又b+c=4,∴c=4-b,∴b2+(4-b)2-b(4-b)=4,整理得b2-4b+4=0,
∴b=2,∴c=4-b=2,∴b=c=a,
故△ABC为等边三角形.(15分)
17.解析 (1)由正弦定理及bsin A+atan Acos B=2asin C得,
sin Bsin A+sin Atan Acos B=2sin Asin C,(2分)
∵sin A≠0,所以sin B+cos B=2sin C,即sin Bcos A+cos Bsin A=2sin Ccos A,
即sin(B+A)=sin C=2sin Ccos A,(4分)
又sin C≠0,所以cos A=,(5分)
又A∈.(6分)
(2)在△ABD中,∠BAD=, (7分)
由正弦定理得,
在△ACD中,由正弦定理得,
则AD=,(9分)
所以,
所以. (11分)
因为△ABC为锐角三角形,∠CAD=,
所以, (13分)
因为tan+2,
所以,
从而1<.
故).(15分)
18.解析 (1)因为五边形ABCDE是正五边形,
所以∠EAB=,∠EAD=∠DAC=∠CAB,
所以∠EAB=3∠DAC,所以∠DAC=,
在△DAC中,DC=1,∠ADC=,(2分)
由正弦定理得,
所以AC=,(5分)
所以劣弧DC的长为,(6分)
所以勒洛五边形ABCDE的周长l1=5×.(8分)
(2)l1如图所示,作出正五边形ABCDE的外接圆,
由(1)知,∠AEB=,
所以由圆心角与圆周角的关系得∠AOB=2∠AEB=,
在△AOB中,AB=1,OA=OB,∠AOB=,
由余弦定理,得AB2=OA2+OB2-2×OA×OB×cos∠AOB,
即1=2×OA2×,(10分)
因为cos-1=2×,
所以1=2×OA2×,(12分)
所以正五边形ABCDE的外接圆的周长l2=2×OA×π=2×π,(14分)
因为<0,(15分)
所以-<0,所以l119.解析 (1)是定值,理由如下:
在△BPM中,∠BMP=180°-60°-45°=75°,(1分)
由正弦定理可得,
所以PM=-1)PB,(2分)
同理可得PN=(-1)PC,(3分)
所以PM+PN=(-1),为定值.(4分)
(2)在△PMN中,∠MPN=60°,由余弦定理可得MN2=PM2+PN2-2PM·PNcos 60°,
即MN2=(PM+PN)2-3PM·PN≥(PM+PN)2-3×,(6分)
所以MN≥,当且仅当PM=PN时,等号成立,
由(1)得PM+PN=400(-1),
所以MN≥200(-1)时,等号成立.(8分)
故当点P是BC的中点时,三条小径PM,PN,MN的长度之和最小,为600(-1)米.(10分)
(3)由(1)可知PM=(-1)PB,
故S△BPM=-1)PB2,(12分)
同理可得S△CPN=-1)PC2,(14分)
所以S△BPM+S△CPN=),(16分)
当且仅当PB=PC=200时等号成立,故郁金香区域面积之和的最小值为20 000(3-)平方米.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第四册
第九章 解三角形
全卷满分150分 考试用时120分钟
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在△ABC中,内角A,B,C的对边分别为a,b,c,则下列等式中成立的是( )
A.asin B=bsin A B.c=
C. D.a+b-c=sin A+sin B-sin C
2.在△ABC中,角A,B,C的对边分别是a,b,c,且a=,bcos A=sin B,则A=( )
A.
3.我舰在岛A南偏西50°方向的B处,且A,B距离为12千米,发现敌舰正离开岛A沿北偏西10°的方向以每小时10千米的速度航行,若我舰要用2小时追上敌舰,则速度大小为( )
A.28千米/时 B.14千米/时
C.14千米/时 D.20千米/时
4.在△ABC中,AB=3,AD⊥AC,且AD交BC于点D,AD=3,则sin C=( )
A.
5.已知△ABC的内角A,B,C的对边分别为a,b,c,若cos C=,bcos A+acos B=2,则△ABC外接圆的面积为 ( )
A.4π B.8π C.9π D.36π
6.在△ABC中,内角A,B,C的对边分别为a,b,c,且A=,b=4,那么满足条件的三角形的个数为( )
A.0 B.1 C.2 D.无数
7.已知△ABC的内角A,B,C的对边分别为a,b,c,S表示三角形的面积,若asin A+bsin B=csin C,S=(a2+c2-b2),则△ABC的形状是( )
A.直角三角形 B.等腰三角形
C.等腰或直角三角形 D.等腰直角三角形
8.如图甲,首钢滑雪大跳台是冬奥历史上第一座与工业遗产再利用直接结合的竞赛场馆,大跳台的设计中融入了世界文化遗产敦煌壁画中“飞天”的元素.如图乙,某研究性学习小组为了估算赛道造型最高点A距离地面的高度AB(AB与地面垂直),在赛道一侧找到一座建筑物CD,测得CD的高度为h,并从C点测得A点的仰角为30°;在赛道与建筑物CD之间的地面上的点E处测得A点,C点的仰角分别为75°和30°(其中B,E,D三点共线).该学习小组利用这些数据得AB约为60米,则CD的高h约为( )
(参考数据:≈2.45)
A.11米 B.20.8米 C.25.4米 D.31.8米
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列命题中,正确的是( )
A.在△ABC中,A>B,则sin A>sin B
B.在锐角△ABC中,不等式sin A>cos B恒成立
C.在△ABC中,若acos A=bcos B,则△ABC必是等腰直角三角形
D.在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形
10.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=5,b=6,c=7,下列说法正确的是( )
A.sin A∶sin B∶sin C=5∶6∶7
B.cos A∶cos B∶cos C=5∶6∶7
C.△ABC是锐角三角形
D.△ABC的最大内角是最小内角的2倍
11.在△ABC中,角A,B,C的对边分别为a,b,c,如果a,b,c满足a≤(b+c),那么下列结论中正确的是( )
A.sin A≤(sin B+sin C)
B.△ABC不可能是直角三角形
C.角A一定是锐角
D.角A一定是钝角
三、填空题(本大题共3小题,每小题5分,共15分.将答案填在题中横线上)
12.已知△ABC中,AB=cos B=0,则△ABC的面积为 .
13.若a,a+1,a+2是钝角三角形的三边,则a的取值范围是 .
14.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知bcos C+ccos B=3acos A,若S为△ABC的面积,则当的值为 .
四、解答题(本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知.
(1)求证:△ABC为等腰三角形;
(2)从条件①、条件②、条件③这三个条件中选择一个作为已知条件,使△ABC存在且唯一,求b的值.
条件①:B=;条件③:AB边上的高为3.
16.(15分)已知a,b,c分别是△ABC的内角A,B,C的对边,满足acsin A+4sin C=4csin A.
(1)求a的值;
(2)△ABC的外接圆为圆O(O在△ABC内部),S△OBC=,b+c=4,判断△ABC的形状,并说明理由.
17.(15分)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,bsin A+atan A·cos B=2asin C.
(1)求A;
(2)若D为BC延长线上一点,且∠CAD=的取值范围.
18.(17分)勒洛三角形是由19世纪德国工程师勒洛在研究机械分类时发现的.如图1,以等边三角形ABC的每个顶点为圆心、边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形就是勒洛三角形ABC.受此启发,某数学兴趣小组绘制了勒洛五边形.如图2,分别以正五边形ABCDE的各顶点为圆心,对角线长为半径,在距离该顶点较远的另外两个顶点间画一段圆弧,五段圆弧围成的曲边五边形就是勒洛五边形ABCDE.设正五边形ABCDE的边长为1.
(1)求勒洛五边形ABCDE的周长l1;
(2)设正五边形ABCDE的外接圆的周长为l2,试比较l1与l2的大小,并说明理由.
图1 图2
19.(17分)某农场有一块等腰直角三角形的空地ABC,其中斜边BC的长度为400米,为迎接“五一”观光游,欲在边界BC上选择一点P,修建观赏小径PM,PN,其中M,N分别在边界AB,AC上,小径PM,PN与边界BC的夹角都是60°,区域PMB和区域PNC内种植郁金香,区域AMPN内种植月季花.
(1)探究观赏小径PM,PN的长度之和是不是定值 请说明理由;
(2)为深度体验观赏,准备在月季花区域内修建小径MN,当点P在何处时,三条小径PM,PN,MN的长度之和最小
(3)求郁金香区域面积之和的最小值.
答案全解全析
1.A 由正弦定理可得,所以asin B=bsin A.
2.D 由bcos A=sin B得,
又a=,
又A∈(0,π),所以A=.故选D.
3.B 如图,设我舰在C处追上敌舰,速度大小为v,在△ABC中,AC=10×2=20(千米),AB=12(千米),∠BAC=120°,所以BC2=AB2+AC2-2AB·ACcos 120°=784,所以BC=28(千米),故v=14千米/时.
4.B 由cos∠BAC=-
=-cos∠BAC=,
又∠BAD为锐角,所以cos∠BAD=,
在△ABD中,由余弦定理得BD=,
所以sin C=cos∠ADC=-cos∠ADB=-
=-.故选B.
5.C 设△ABC外接圆的半径为R,由题意及余弦定理得b·=2,解得c=2,
由cos C==6,所以R=3,
所以△ABC外接圆的面积为πR2=9π.
6.C 在△ABC中,A=,b=4,由a2=b2+c2-2bccos A,可得
14=16+c2-4c,即c2-4c+2=0,解得c=2±,
所以满足条件的三角形的个数为2,故选C.
7.D 由asin A+bsin B=csin C得a2+b2=c2,所以△ABC是直角三角形.
又由三角形的面积公式得×2accos B,整理得tan B=1,因此B=45°,故△ABC是等腰直角三角形.
8.C 由题意知∠AEB=75°,∠CED=30°,则∠AEC=75°,∠ACE=60°,∠CAE=45°,在Rt△ABE中,AE=,
在△ACE中,,
则CE=,
∵sin 75°=sin(45°+30°)=,
∴CD=≈60-20×1.73=25.4(米),
∴CD的高h约为25.4米,故选C.
9.ABD 对于A,由A>B可得a>b,利用正弦定理可得sin A>sin B,故A正确;
对于B,在锐角△ABC中,A,B∈,
∵A+B>=cos B,故B正确;
对于C,在△ABC中,由acos A=bcos B及正弦定理可得sin Acos A=sin Bcos B,∴sin 2A=sin 2B,
∵A,B∈(0,π),∴2A=2B或2A=π-2B,∴A=B或A+B=,
∴△ABC是等腰三角形或直角三角形,故C错误;
对于D,B=60°,b2=ac,结合余弦定理可得ac=b2=a2+c2-ac,∴(a-c)2=0,解得a=c,所以A=C=B=60°,∴△ABC是等边三角形,故D正确.
故选ABD.
10.AC 对于A,由正弦定理可得sin A∶sin B∶sin C=a∶b∶c=5∶6∶7,A正确;
对于B,由余弦定理可得cos A=,
所以cos A∶cos B∶cos C=25∶19∶7,B错误;
对于C,因为a
对于D,由题意知,A为最小角,则cos 2A=2cos2A-1=2×,所以2A∈(0,π),
所以C≠2A,D错误.
故选AC.
11.AC 由正弦定理结合已知条件易知A选项正确;
当△ABC是直角三角形且a是较短的直角边时,a≤(b+c)成立,故B选项错误;
将不等式两边平方得a2≤(当且仅当b=c时,第二个等号成立),因为A为三角形的内角,所以0°
解析 由sin B+.
13.答案 1
所以解得1
解析 由正弦定理及bcos C+ccos B=3acos A,
可得sin Bcos C+sin Ccos B=3sin Acos A,
所以sin(B+C)=sin A=3sin Acos A,
因为A∈(0,π),所以sin A≠0,
所以cos A=.
由余弦定理得a2=b2+c2-2bccos A=b2+c2-bc,
又S=,
当且仅当b=c时取“=”,
此时a2=b2+c2-c2,
所以a=+1.
15.解析 (1)证明:由a,
在△ABC中,由余弦定理可得a2=,(3分)
整理,得(a-c)(3a+5c)=0,故有a=c,
故△ABC为等腰三角形.(6分)
(2)选择条件①:B=.
由(1)知a=c,则有A=C=,
此时cos A=cos,
与已知矛盾,三角形无解,不可选.(8分)
选择条件②:△ABC的面积为.
因为cos A=.
由(1)知a=c,则有A=C,所以sin B=sin(π-2A)=sin 2A=2sin Acos A=2×,(11分)
又S△ABC=,所以a=c=5.
由正弦定理得.
三角形存在且唯一,可选.(13分)
选择条件③:AB边上的高为3.同条件②得sin B=,(11分)
因此a=.三角形存在且唯一,可选.(13分)
16.解析 (1)由正弦定理及acsin A+4sin C=4csin A得a2c+4c=4ac,
∵c≠0,∴a2+4=4a,∴(a-2)2=0,∴a=2.(4分)
(2)△ABC为等边三角形,理由如下:(5分)
记BC的中点为D,连接OD,易知OD⊥BC.
则S△OBC=,故∠BOC=120°,
故A=∠BOC=60°,(9分)
由余弦定理可知,a2=b2+c2-2bccos A,即4=b2+c2-bc,
又b+c=4,∴c=4-b,∴b2+(4-b)2-b(4-b)=4,整理得b2-4b+4=0,
∴b=2,∴c=4-b=2,∴b=c=a,
故△ABC为等边三角形.(15分)
17.解析 (1)由正弦定理及bsin A+atan Acos B=2asin C得,
sin Bsin A+sin Atan Acos B=2sin Asin C,(2分)
∵sin A≠0,所以sin B+cos B=2sin C,即sin Bcos A+cos Bsin A=2sin Ccos A,
即sin(B+A)=sin C=2sin Ccos A,(4分)
又sin C≠0,所以cos A=,(5分)
又A∈.(6分)
(2)在△ABD中,∠BAD=, (7分)
由正弦定理得,
在△ACD中,由正弦定理得,
则AD=,(9分)
所以,
所以. (11分)
因为△ABC为锐角三角形,∠CAD=,
所以, (13分)
因为tan+2,
所以,
从而1<.
故).(15分)
18.解析 (1)因为五边形ABCDE是正五边形,
所以∠EAB=,∠EAD=∠DAC=∠CAB,
所以∠EAB=3∠DAC,所以∠DAC=,
在△DAC中,DC=1,∠ADC=,(2分)
由正弦定理得,
所以AC=,(5分)
所以劣弧DC的长为,(6分)
所以勒洛五边形ABCDE的周长l1=5×.(8分)
(2)l1
由(1)知,∠AEB=,
所以由圆心角与圆周角的关系得∠AOB=2∠AEB=,
在△AOB中,AB=1,OA=OB,∠AOB=,
由余弦定理,得AB2=OA2+OB2-2×OA×OB×cos∠AOB,
即1=2×OA2×,(10分)
因为cos-1=2×,
所以1=2×OA2×,(12分)
所以正五边形ABCDE的外接圆的周长l2=2×OA×π=2×π,(14分)
因为<0,(15分)
所以-<0,所以l1
在△BPM中,∠BMP=180°-60°-45°=75°,(1分)
由正弦定理可得,
所以PM=-1)PB,(2分)
同理可得PN=(-1)PC,(3分)
所以PM+PN=(-1),为定值.(4分)
(2)在△PMN中,∠MPN=60°,由余弦定理可得MN2=PM2+PN2-2PM·PNcos 60°,
即MN2=(PM+PN)2-3PM·PN≥(PM+PN)2-3×,(6分)
所以MN≥,当且仅当PM=PN时,等号成立,
由(1)得PM+PN=400(-1),
所以MN≥200(-1)时,等号成立.(8分)
故当点P是BC的中点时,三条小径PM,PN,MN的长度之和最小,为600(-1)米.(10分)
(3)由(1)可知PM=(-1)PB,
故S△BPM=-1)PB2,(12分)
同理可得S△CPN=-1)PC2,(14分)
所以S△BPM+S△CPN=),(16分)
当且仅当PB=PC=200时等号成立,故郁金香区域面积之和的最小值为20 000(3-)平方米.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
