2025人教B版高中数学必修第四册强化练习题(含解析)--第十一章 立体几何初步
文档属性
| 名称 | 2025人教B版高中数学必修第四册强化练习题(含解析)--第十一章 立体几何初步 |

|
|
| 格式 | docx | ||
| 文件大小 | 766.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 11:15:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学必修第四册
第十一章 立体几何初步
全卷满分150分 考试用时120分钟
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,△A'B'C'是△ABC的直观图,其中B'O'=C'O'=1,A'O'=,那么△ABC是( )
A.等边三角形 B.直角三角形
C.等腰非等边三角形 D.无法确定
2.已知m,n是两条不同的直线,α,β是两个不重合的平面,那么下面给出的条件中,一定能推出m⊥β的是( )
A.α∥β,且m α B.m∥n,且n⊥β
C.m⊥n,且n β D.m⊥n,且n∥β
3.如图,某无盖容器可视为一个球被两个平行平面所截后剩下的部分,其中球面被平面所截的部分均可视为球冠(截得的圆面是底,垂直于圆面的直径被截得的部分是高,其面积公式为S=2πRh,其中R为球的半径,h为球冠的高).已知该几何体的高为38 cm,在高为20 cm处有最大直径(外径),为48 cm,则该几何体的外表面积约为(π≈3.14)( )
A.6 270 cm2 B.6 275 cm2
C.6 280 cm2 D.6 300 cm2
4.在长方体ABCD-A1B1C1D1中,AA1=AD,则异面直线B1D与CD1所成角的余弦值是( )
A.
C.
5.如图所示的是一个陀螺的立体结构图.已知底面圆的直径AB=16 cm,圆柱体部分的高BC=8 cm,圆锥体部分的高CD=6 cm,则这个陀螺的表面积是( )
A.192π cm2 B.252π cm2
C.272π cm2 D.336π cm2
6.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G分别为A1D1,A1B1,BB1的中点,过E,F,G三点的平面截正方体ABCD-A1B1C1D1所得的截面面积为( )
A.4 B.4
C.
7.正方体ABCD-A1B1C1D1中,P为正方形ABCD内一点(不含边界),记O为正方形ABCD的中心,直线PA1,PB1,PC1,PD1与平面A1B1C1D1所成的角分别为θ1,θ2,θ3,θ4.若θ1=θ3,θ2>θ4,则点P在( )
A.线段OA上 B.线段OB上
C.线段OC上 D.线段OD上
8.已知棱长为的正方体ABCD-A1B1C1D1内有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为( )
A.3π
C.
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
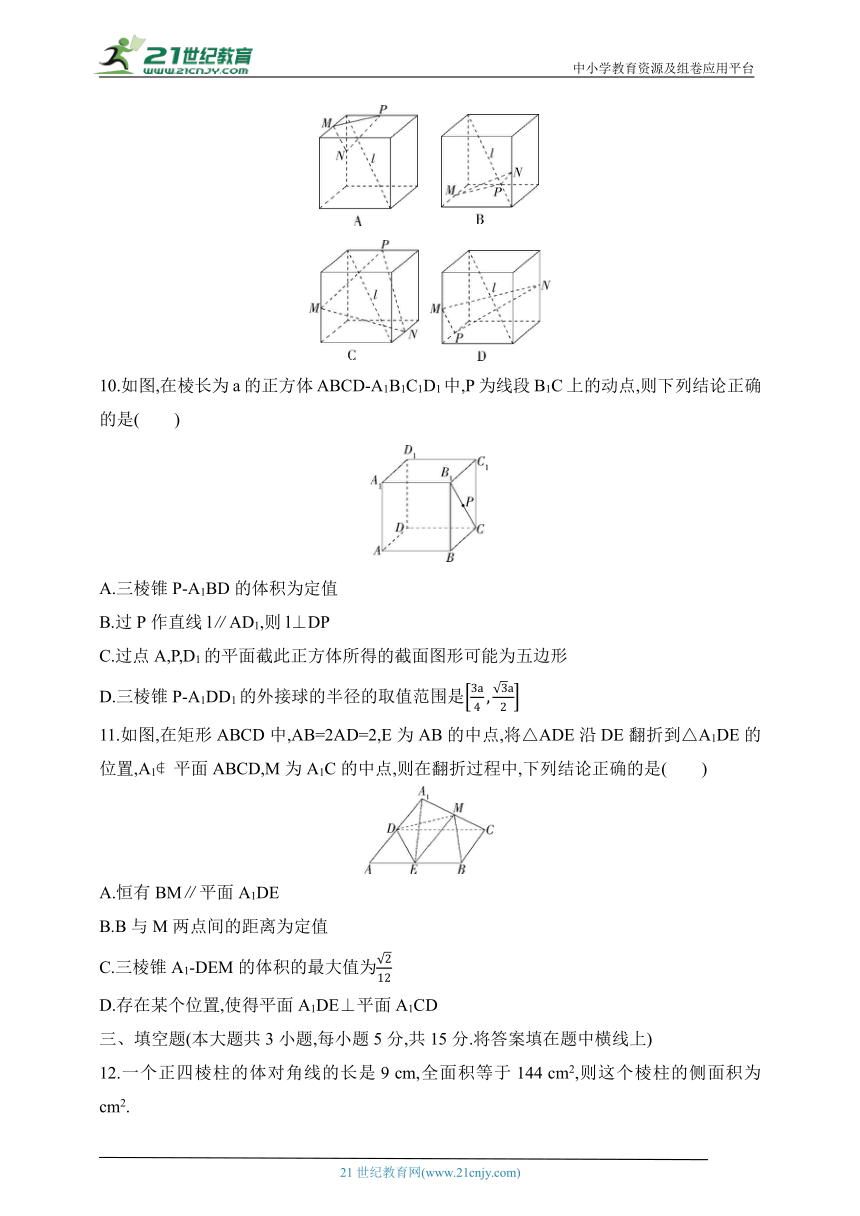
9.如图所示,在四个正方体中,l是正方体的一条体对角线,点M,N,P分别为其所在棱的中点,能得出l⊥平面MNP的图形为( )
10.如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为线段B1C上的动点,则下列结论正确的是( )
A.三棱锥P-A1BD的体积为定值
B.过P作直线l∥AD1,则l⊥DP
C.过点A,P,D1的平面截此正方体所得的截面图形可能为五边形
D.三棱锥P-A1DD1的外接球的半径的取值范围是
11.如图,在矩形ABCD中,AB=2AD=2,E为AB的中点,将△ADE沿DE翻折到△A1DE的位置,A1 平面ABCD,M为A1C的中点,则在翻折过程中,下列结论正确的是( )
A.恒有BM∥平面A1DE
B.B与M两点间的距离为定值
C.三棱锥A1-DEM的体积的最大值为
D.存在某个位置,使得平面A1DE⊥平面A1CD
三、填空题(本大题共3小题,每小题5分,共15分.将答案填在题中横线上)
12.一个正四棱柱的体对角线的长是9 cm,全面积等于144 cm2,则这个棱柱的侧面积为 cm2.
13.四棱锥P-ABCD的底面是边长为1的正方形,如图所示,点E是棱PD上一点,PE=PD,若=λ且满足BF∥平面ACE,则λ= .
14.在正四面体ABCD中,点E,F分别在棱AB,AC上,满足BE=1,EF=2,EF∥平面BCD,则棱AB的长为 ,以点A为球心,为半径作一个球,则该球球面与正四面体ABCD的表面相交所得到的曲线长度之和为 .(本题第一空2分,第二空3分)
四、解答题(本大题共5小题,共17分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)如图,在长方体ABCD-A1B1C1D1中,BC=CC1,点E,F分别在BC,CC1上(不包含端点),且CE=CF.
证明:(1)A,D1,E,F四点共面;
(2)直线AE,D1F,DC交于一点.
16.(15分)如图,在多面体ABCDEF中,AD,BE,CF均垂直于平面ABC,AC=BC,AD=2,BE=4,CF=3.
(1)过CF的平面α与平面ABED垂直,请在图中作出平面α截此多面体所得的截面,并说明理由;
(2)若∠ACB=120°,AB=4,求多面体ABCDEF的体积.
17.(15分)如图,在四面体ABCD中,已知AB=AC=AD=BC=CD=a,BD=a.
(1)求证:AC⊥BD;
(2)求直线AC与平面BCD所成的角;
(3)求二面角A-BC-D的正切值.
18.(17分)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC的体积的最大值;
(3)若BC=,点E在线段PB上,求CE+OE的最小值.
19.(17分)如图1,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC=2BC,E为AB的中点,沿DE将△ADE折起,使得点A到点P的位置,且PE⊥EB,M为PB的中点,N是BC上的动点(与点B,C不重合),如图2.
(1)证明:平面EMN⊥平面PBC;
(2)是否存在点N,使得二面角B-EN-M的平面角的正切值为 若存在,确定点N的位置;若不存在,请说明理由.
图1 图2
答案全解全析
1.A 如图,将直观图还原,则BO=CO=1,AO=,所以△ABC是等边三角形.故选A.
2.B A中,可推出m∥β,故A错误;易知B正确;C、D中,可推出m β或m∥β或m与β相交,故C、D错误.
3.C 由题意可知球的半径R=24 cm,上部分球冠的高为24-18=6 cm,下部分球冠的高为24-20=4 cm,设下底面圆的半径为r cm,则r2=242-202=176,
所以该瓷器的外表面积为4π×242-2π×24×6-2π×24×4+π×176=2 000π≈6 280(cm2).故选C.
4.D 如图,连接A1C,记A1C∩B1D=F,则F是A1C的中点,取A1D1的中点E,连接B1E,EF,易证EF∥CD1,EF=CD1,则∠B1FE(或其补角)是异面直线B1D与CD1所成的角.
设AB=2,则B1E=,B1F=2.
在△B1EF中,由余弦定理可得cos∠B1FE=,
故异面直线B1D与CD1所成角的余弦值为,故选D.
5.C 由题意可得圆锥体的母线长为=10(cm),
所以圆锥体的侧面积为10×8π=80π(cm2).
易得圆柱体的侧面积为16π×8=128π(cm2),圆柱体的底面面积为π×82=64π(cm2),
所以陀螺的表面积为80π+128π+64π=272π(cm2).故选C.
6.D 如图,分别取BC的中点H,CD的中点I,DD1的中点K,连接GH,HI,IK,KE,因为该几何体为正方体,所以EF∥HI,FG∥IK,GH∥KE,且EF=HI=FG=IK=GH=KE=.故选D.
7.B 因为直线PA1,PB1,PC1,PD1与平面A1B1C1D1所成角的大小分别为θ1,θ2,θ3,θ4,所以直线PA1,PB1,PC1,PD1与直线AA1,BB1,CC1,DD1所成角的大小,分别为-θ4,
由θ1=θ3,可知P在线段BD上,又θ2>θ4,所以-θ4,即PB1与BB1所成的角更小,则点P在线段OB上.故选B.
8.D 由题知,只需考虑圆柱的底面与正方体的表面相切的情况,由图形的对称性可知,侧面积最大时,圆柱的上底面必与过A点的三个面相切,且切点分别在线段AB1,AC,AD1上,如图所示,设线段AB1上的切点为E,AC1与平面A1BD的交点为O2,圆柱上底面的圆心为O1,半径即为O1E,记为r,设AB1与平面A1BD的交点为F.
∵正方体ABCD-A1B1C1D1的棱长为.
由题意知,O2F=AC1=1.
由O1E∥O2F知,O1E,
则圆柱的高为3-2AO1=3-2r,
∴S圆柱侧=2πr(3-2π.
∴当r=.
9.AD A中,如图所示,连接AC,BD.
∵M,P分别为其所在棱的中点,∴MP∥AC.∵四边形ABCD为正方形,∴AC⊥BD,∵BB'⊥平面ABCD,AC 平面ABCD,∴BB'⊥AC,
∵BD∩BB'=B,BD,BB' 平面DBB',∴AC⊥平面DBB',
∵DB' 平面DBB',∴AC⊥DB'.∵MP∥AC,∴DB'⊥MP,
同理,DB'⊥NP,∵MP∩NP=P,MP,NP 平面MNP,
∴DB'⊥平面MNP,即l⊥平面MNP,故A正确.
D中,由A中证明同理可证l⊥MP,l⊥MN,
又∵MP∩MN=M,MP,MN 平面MNP,∴l⊥平面MNP,故D正确.故选AD.
10.ABD 对于A,如图1,连接A1D,A1B,BD,则B1C∥A1D,
因为A1D 平面A1BD,B1C 平面A1BD,所以B1C∥平面A1BD,
所以动点P到平面A1BD的距离为定值,因为△A1BD的面积为定值,所以三棱锥P-A1BD的体积为定值,故A正确;
对于B,如图2,连接AD1,A1D,DP,由正方体的性质可知AD1⊥A1D,AD1⊥A1B1,因为A1D∩A1B1=A1,A1D,A1B1 平面A1DCB1,所以AD1⊥平面A1DCB1,因为DP 平面A1DCB1,所以AD1⊥DP,
又因为l∥AD1,所以l⊥DP,故B正确;
对于C,如图3,连接BC1,AD1,当P为B1C的中点时,过点A,P,D1的平面为平面ABC1D1,当点P从B1C的中点向点B1运动时,截面过平面ADD1A1,AA1B1B,BCC1B1,A1B1C1D1,当点P从B1C的中点向点C运动时,截面过平面ADD1A1,ABCD,BCC1B1,DCC1D1,则过点A,P,D1的平面最多与正方体的四个面相交,所以截面图形最多为四边形,故C错误;
图3
对于D,连接A1D,AD1,且A1D与AD1相交于点E,则E为A1D的中点,
所以在△A1DD1中,E到各顶点的距离相等,过E作EF⊥平面A1DD1,交B1C于F,则球心O一定在EF上,且OA1=OP,
设球的半径为r,由题意可得A1D=a,
当点P与点F重合时,a-a,此时r最小;
当点P与点B1或点C重合时,△A1EO≌△B1FO,
所以r=a,此时r最大.
所以三棱锥P-A1DD1的外接球的半径的取值范围是,故D正确.故选ABD.
11.ABC 取A1D的中点N,连接MN,EN,易证四边形BMNE是平行四边形,所以BM∥EN,因为BM 平面A1DE,EN 平面A1DE,所以BM∥平面A1DE,故A正确;
易知DN=,∠A1DE=∠ADE=45°,
在△DEN中,根据余弦定理得EN2=,故B正确;
连接EC,因为M为A1C的中点,所以=2=2,
故=S△CDE·h,其中h表示A1到平面ABCD的距离,当平面A1DE⊥平面ABCD时,h达到最大值,此时,故C正确;
假设平面A1DE⊥平面A1CD,又平面A1DE∩平面A1CD=A1D,A1E⊥A1D,A1E 平面A1DE,所以A1E⊥平面A1CD,所以A1E⊥A1C,
在Rt△A1CE中,A1E=1,EC=,所以A1C=1.
又因为A1D=1,CD=2,所以A1D+A1C=CD,故A1,C,D三点共线,
所以A1∈CD,得A1∈平面ABCD,与题干矛盾,故D不正确.故选ABC.
12.答案 112或72
解析 设正四棱柱的底面边长、侧棱长分别为a cm,l cm,
则
∴S棱柱侧=4×4×7=112(cm2)或S棱柱侧=4×6×3=72(cm2).
13.答案
解析 如图,连接BD,交AC于点O,连接OE,由四边形ABCD是正方形,得BO=OD,在线段PE上取点G,使得GE=ED,由PE=,
连接BG,FG,则BG∥OE,由OE 平面ACE,BG 平面ACE,
得BG∥平面ACE,而BF∥平面ACE,BG∩BF=B,BG,BF 平面BGF,
因此平面BGF∥平面ACE,又平面PCD∩平面ACE=EC,平面PCD∩平面BGF=GF,则GF∥EC,所以λ=.
14.答案 3;
解析 因为EF∥平面BCD,EF 平面ABC,平面ABC∩平面BCD=BC,所以EF∥BC,
因为正四面体ABCD的每个面都是等边三角形,所以△AEF也为等边三角形,所以AB=BE+AE=1+2=3.
该球球面与正四面体的四个面都相交,所得的交线分为两类:一类是球面与三个侧面ABD,ABC,ACD的交线,与侧面ABC的交线为,,
又AB=3,∠BAC=60°,
所以,
球面与侧面ABD,ACD的交线与一样长,
另一类是球面与底面BCD的交线,过D作DP⊥BC,垂足为P,过A作AO⊥DP,垂足为O,则OD=,
所以AO=,故球面与底面BCD刚好相交于底面BCD各边的中点处,此时形成的交线是底面BCD的内切圆,
则内切圆半径为OP=,
故内切圆的周长为2π×π,
因此所有的交线长为3×.
15.证明 (1)如图,连接AD1,EF,BC1.
因为BC=CC1,CE=CF,所以,所以EF∥BC1.(3分)
由长方体的性质可知AD1∥BC1,所以AD1∥EF.
所以A,D1,E,F四点共面.(6分)
(2)由(1)可得AD1∥EF,AD1≠EF,则四边形AEFD1是梯形,
故直线AE与直线D1F必相交,记AE∩D1F=P.(8分)
因为P∈AE,且AE 平面ABCD,所以P∈平面ABCD,
因为P∈D1F,且D1F 平面CDD1C1,所以P∈平面CDD1C1.(10分)
因为平面ABCD∩平面CDD1C1=CD,所以P∈CD,
即直线AE,D1F,DC交于一点.(13分)
16.解析 (1)如图,分别取AB,DE的中点G,H,连接CG,FH,HG,则截面CFHG即为所求.
(3分)
理由如下:
因为AD,BE,CF均垂直于平面ABC,所以AD∥BE∥CF,
因为AD=2,BE=4,所以四边形ABED为梯形.
又G,H分别为AB,DE的中点,所以HG∥BE,HG=3,
所以HG∥CF,HG=CF,所以四边形CFHG为平行四边形.
因为AC=BC,G为AB的中点,所以CG⊥AB.
因为AD⊥平面ABC,CG 平面ABC,所以AD⊥CG.(5分)
因为AB∩AD=A,所以CG⊥平面ABED,又CG 平面CFHG,所以平面CFHG⊥平面ABED,所以截面CFHG即为所求.(6分)
(2)解法一:如图,过点A作AM⊥BC,交BC的延长线于点M.
因为BE⊥平面ABC,AM 平面ABC,所以BE⊥AM,
又BC∩BE=B,BC,BE 平面BCFE,所以AM⊥平面BCFE.(9分)
在△ABC中,AC=BC,∠ACB=120°,AB=4,易得AC=BC=4,
所以S△ABC=.
因为AM=AC·sin60°=4×,
所以VD-BCFE=,(11分)
VD-ABC=,(13分)
所以V多面体ABCDEF=VD-ABC+VD-BCFE=.(15分)
解法二:如图,将多面体ABCDEF补成直三棱柱ABC-A'B'C',
其中A'D=4,B'E=2,C'F=3,AA'=6,
则V多面体ABCDEF=VABC-A'B'C',(9分)
在△ABC中,AC=BC,∠ACB=120°,AB=4,易得AC=BC=4,
所以S△ABC=,(13分)
所以VABC-A'B'C'=S△ABC·AA'=4,
所以V多面体ABCDEF=12.(15分)
解法三:如图,在多面体ABCDEF中作直三棱柱ABC-DPQ,
则V多面体ABCDEF=VABC-DPQ+VD-EFQP,(9分)
过点A作AM⊥BC,交BC的延长线于点M,
因为BE⊥平面ABC,AM 平面ABC,所以BE⊥AM,
又BC∩BE=B,BC,BE 平面BCFE,所以AM⊥平面BCFE.
在△ABC中,AC=BC,∠ACB=120°,AB=4,易得AC=BC=4,
所以S△ABC=,(12分)
因为AM=AC·sin60°=4×,
所以VABC-DPQ=S△ABC·AD=4,
VD-EFQP=,
所以V多面体ABCDEF=VABC-DPQ+VD-EFQP=8.(15分)
17.解析 (1)证明:取BD的中点E,连接AE,CE,因为AB=AD=BC=CD,所以BD⊥CE,BD⊥AE,(2分)
因为AE∩CE=E,AE,CE 平面ACE,所以BD⊥平面ACE,
因为AC 平面ACE,所以AC⊥BD.(4分)
(2)因为AB=AC=AD=BC=CD=a,BD=a,
又AE2+CE2=a2=a2=AC2,所以△ACE为等腰直角三角形,且AE⊥CE,(6分)
又AE⊥BD,BD∩CE=E,BD,CE 平面BCD,所以AE⊥平面BCD,
所以直线AC与平面BCD所成的角为∠ACE,(8分)
在Rt△AEC中,AE=CE,
所以∠ACE=45°,所以直线AC与平面BCD所成的角为45°.(9分)
(3)取BC的中点F,连接AF,EF,则EF∥CD,且EF=,(10分)
因为BC2+CD2=a2+a2=2a2=BD2,所以BC⊥CD,
所以BC⊥EF,(11分)
因为AB=AC=BC,所以BC⊥AF,
所以∠AFE是二面角A-BC-D的平面角,(13分)
在Rt△AEF中,tan∠AFE=,
即二面角A-BC-D的正切值为.(15分)
18.解析 (1)证明:在△AOC中,
因为OA=OC,D为AC的中点,所以AC⊥DO.
又PO垂直于圆O所在的平面,所以PO⊥AC.(2分)
因为DO∩PO=O,DO,PO 平面PDO,
所以AC⊥平面PDO.(4分)
(2)因为点C在圆O上,
所以当CO⊥AB时,C到AB的距离最大,且最大值为1.
又AB=2OB=2,所以△ABC面积的最大值为×2×1=1.(7分)
因为三棱锥P-ABC的高PO=1,
所以三棱锥P-ABC的体积的最大值为.(10分)
(3)在△POB中,PO=OB=1,∠POB=90°,
所以PB=,所以PB=PC=BC.
在三棱锥P-ABC中,将△BCP绕直线PB旋转至△BC'P,使之与△ABP共面,如图所示.
当O,E,C'共线时,CE+OE取得最小值.(14分)
因为OP=OB,C'P=C'B,所以OC'垂直平分PB,则E为PB的中点.
从而OC'=OE+EC'=,
即CE+OE的最小值为.(17分)
19.解析 (1)证明:因为PE⊥ED,PE⊥EB,
EB∩ED=E,EB,ED 平面EBCD,所以PE⊥平面EBCD,
因为BC 平面EBCD,所以PE⊥BC,
因为BC⊥EB,EB∩PE=E,EB,PE 平面PEB,
所以BC⊥平面PEB,(2分)
因为EM 平面PEB,所以BC⊥EM,
因为PE=EB,PM=MB,所以EM⊥PB,(4分)
因为BC∩PB=B,BC,PB 平面PBC,所以EM⊥平面PBC,
因为EM 平面EMN,所以平面EMN⊥平面PBC.(7分)
(2)假设存在点N满足题意,如图,过M作MQ⊥EB于Q,
因为PE⊥EB,所以PE∥MQ,
由(1)知,PE⊥平面EBCD,所以MQ⊥平面EBCD,
因为EN 平面EBCD,所以MQ⊥EN,(10分)
过Q作QR⊥EN于R,连接MR,
因为MQ∩QR=Q,MQ,QR 平面MQR,所以EN⊥平面MQR,
因为MR 平面MQR,所以EN⊥MR,
所以∠MRQ为二面角B-EN-M的平面角,(12分)
不妨设PE=EB=BC=2,则MQ=1,
在Rt△EBN中,设BN=x(0所以,(14分)
所以tan∠MRQ=,又0此时N为BC的中点.
综上,存在点N,使得二面角B-EN-M的平面角的正切值为,此时N为BC的中点.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学必修第四册
第十一章 立体几何初步
全卷满分150分 考试用时120分钟
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,△A'B'C'是△ABC的直观图,其中B'O'=C'O'=1,A'O'=,那么△ABC是( )
A.等边三角形 B.直角三角形
C.等腰非等边三角形 D.无法确定
2.已知m,n是两条不同的直线,α,β是两个不重合的平面,那么下面给出的条件中,一定能推出m⊥β的是( )
A.α∥β,且m α B.m∥n,且n⊥β
C.m⊥n,且n β D.m⊥n,且n∥β
3.如图,某无盖容器可视为一个球被两个平行平面所截后剩下的部分,其中球面被平面所截的部分均可视为球冠(截得的圆面是底,垂直于圆面的直径被截得的部分是高,其面积公式为S=2πRh,其中R为球的半径,h为球冠的高).已知该几何体的高为38 cm,在高为20 cm处有最大直径(外径),为48 cm,则该几何体的外表面积约为(π≈3.14)( )
A.6 270 cm2 B.6 275 cm2
C.6 280 cm2 D.6 300 cm2
4.在长方体ABCD-A1B1C1D1中,AA1=AD,则异面直线B1D与CD1所成角的余弦值是( )
A.
C.
5.如图所示的是一个陀螺的立体结构图.已知底面圆的直径AB=16 cm,圆柱体部分的高BC=8 cm,圆锥体部分的高CD=6 cm,则这个陀螺的表面积是( )
A.192π cm2 B.252π cm2
C.272π cm2 D.336π cm2
6.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G分别为A1D1,A1B1,BB1的中点,过E,F,G三点的平面截正方体ABCD-A1B1C1D1所得的截面面积为( )
A.4 B.4
C.
7.正方体ABCD-A1B1C1D1中,P为正方形ABCD内一点(不含边界),记O为正方形ABCD的中心,直线PA1,PB1,PC1,PD1与平面A1B1C1D1所成的角分别为θ1,θ2,θ3,θ4.若θ1=θ3,θ2>θ4,则点P在( )
A.线段OA上 B.线段OB上
C.线段OC上 D.线段OD上
8.已知棱长为的正方体ABCD-A1B1C1D1内有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为( )
A.3π
C.
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.如图所示,在四个正方体中,l是正方体的一条体对角线,点M,N,P分别为其所在棱的中点,能得出l⊥平面MNP的图形为( )
10.如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为线段B1C上的动点,则下列结论正确的是( )
A.三棱锥P-A1BD的体积为定值
B.过P作直线l∥AD1,则l⊥DP
C.过点A,P,D1的平面截此正方体所得的截面图形可能为五边形
D.三棱锥P-A1DD1的外接球的半径的取值范围是
11.如图,在矩形ABCD中,AB=2AD=2,E为AB的中点,将△ADE沿DE翻折到△A1DE的位置,A1 平面ABCD,M为A1C的中点,则在翻折过程中,下列结论正确的是( )
A.恒有BM∥平面A1DE
B.B与M两点间的距离为定值
C.三棱锥A1-DEM的体积的最大值为
D.存在某个位置,使得平面A1DE⊥平面A1CD
三、填空题(本大题共3小题,每小题5分,共15分.将答案填在题中横线上)
12.一个正四棱柱的体对角线的长是9 cm,全面积等于144 cm2,则这个棱柱的侧面积为 cm2.
13.四棱锥P-ABCD的底面是边长为1的正方形,如图所示,点E是棱PD上一点,PE=PD,若=λ且满足BF∥平面ACE,则λ= .
14.在正四面体ABCD中,点E,F分别在棱AB,AC上,满足BE=1,EF=2,EF∥平面BCD,则棱AB的长为 ,以点A为球心,为半径作一个球,则该球球面与正四面体ABCD的表面相交所得到的曲线长度之和为 .(本题第一空2分,第二空3分)
四、解答题(本大题共5小题,共17分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)如图,在长方体ABCD-A1B1C1D1中,BC=CC1,点E,F分别在BC,CC1上(不包含端点),且CE=CF.
证明:(1)A,D1,E,F四点共面;
(2)直线AE,D1F,DC交于一点.
16.(15分)如图,在多面体ABCDEF中,AD,BE,CF均垂直于平面ABC,AC=BC,AD=2,BE=4,CF=3.
(1)过CF的平面α与平面ABED垂直,请在图中作出平面α截此多面体所得的截面,并说明理由;
(2)若∠ACB=120°,AB=4,求多面体ABCDEF的体积.
17.(15分)如图,在四面体ABCD中,已知AB=AC=AD=BC=CD=a,BD=a.
(1)求证:AC⊥BD;
(2)求直线AC与平面BCD所成的角;
(3)求二面角A-BC-D的正切值.
18.(17分)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC的体积的最大值;
(3)若BC=,点E在线段PB上,求CE+OE的最小值.
19.(17分)如图1,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC=2BC,E为AB的中点,沿DE将△ADE折起,使得点A到点P的位置,且PE⊥EB,M为PB的中点,N是BC上的动点(与点B,C不重合),如图2.
(1)证明:平面EMN⊥平面PBC;
(2)是否存在点N,使得二面角B-EN-M的平面角的正切值为 若存在,确定点N的位置;若不存在,请说明理由.
图1 图2
答案全解全析
1.A 如图,将直观图还原,则BO=CO=1,AO=,所以△ABC是等边三角形.故选A.
2.B A中,可推出m∥β,故A错误;易知B正确;C、D中,可推出m β或m∥β或m与β相交,故C、D错误.
3.C 由题意可知球的半径R=24 cm,上部分球冠的高为24-18=6 cm,下部分球冠的高为24-20=4 cm,设下底面圆的半径为r cm,则r2=242-202=176,
所以该瓷器的外表面积为4π×242-2π×24×6-2π×24×4+π×176=2 000π≈6 280(cm2).故选C.
4.D 如图,连接A1C,记A1C∩B1D=F,则F是A1C的中点,取A1D1的中点E,连接B1E,EF,易证EF∥CD1,EF=CD1,则∠B1FE(或其补角)是异面直线B1D与CD1所成的角.
设AB=2,则B1E=,B1F=2.
在△B1EF中,由余弦定理可得cos∠B1FE=,
故异面直线B1D与CD1所成角的余弦值为,故选D.
5.C 由题意可得圆锥体的母线长为=10(cm),
所以圆锥体的侧面积为10×8π=80π(cm2).
易得圆柱体的侧面积为16π×8=128π(cm2),圆柱体的底面面积为π×82=64π(cm2),
所以陀螺的表面积为80π+128π+64π=272π(cm2).故选C.
6.D 如图,分别取BC的中点H,CD的中点I,DD1的中点K,连接GH,HI,IK,KE,因为该几何体为正方体,所以EF∥HI,FG∥IK,GH∥KE,且EF=HI=FG=IK=GH=KE=.故选D.
7.B 因为直线PA1,PB1,PC1,PD1与平面A1B1C1D1所成角的大小分别为θ1,θ2,θ3,θ4,所以直线PA1,PB1,PC1,PD1与直线AA1,BB1,CC1,DD1所成角的大小,分别为-θ4,
由θ1=θ3,可知P在线段BD上,又θ2>θ4,所以-θ4,即PB1与BB1所成的角更小,则点P在线段OB上.故选B.
8.D 由题知,只需考虑圆柱的底面与正方体的表面相切的情况,由图形的对称性可知,侧面积最大时,圆柱的上底面必与过A点的三个面相切,且切点分别在线段AB1,AC,AD1上,如图所示,设线段AB1上的切点为E,AC1与平面A1BD的交点为O2,圆柱上底面的圆心为O1,半径即为O1E,记为r,设AB1与平面A1BD的交点为F.
∵正方体ABCD-A1B1C1D1的棱长为.
由题意知,O2F=AC1=1.
由O1E∥O2F知,O1E,
则圆柱的高为3-2AO1=3-2r,
∴S圆柱侧=2πr(3-2π.
∴当r=.
9.AD A中,如图所示,连接AC,BD.
∵M,P分别为其所在棱的中点,∴MP∥AC.∵四边形ABCD为正方形,∴AC⊥BD,∵BB'⊥平面ABCD,AC 平面ABCD,∴BB'⊥AC,
∵BD∩BB'=B,BD,BB' 平面DBB',∴AC⊥平面DBB',
∵DB' 平面DBB',∴AC⊥DB'.∵MP∥AC,∴DB'⊥MP,
同理,DB'⊥NP,∵MP∩NP=P,MP,NP 平面MNP,
∴DB'⊥平面MNP,即l⊥平面MNP,故A正确.
D中,由A中证明同理可证l⊥MP,l⊥MN,
又∵MP∩MN=M,MP,MN 平面MNP,∴l⊥平面MNP,故D正确.故选AD.
10.ABD 对于A,如图1,连接A1D,A1B,BD,则B1C∥A1D,
因为A1D 平面A1BD,B1C 平面A1BD,所以B1C∥平面A1BD,
所以动点P到平面A1BD的距离为定值,因为△A1BD的面积为定值,所以三棱锥P-A1BD的体积为定值,故A正确;
对于B,如图2,连接AD1,A1D,DP,由正方体的性质可知AD1⊥A1D,AD1⊥A1B1,因为A1D∩A1B1=A1,A1D,A1B1 平面A1DCB1,所以AD1⊥平面A1DCB1,因为DP 平面A1DCB1,所以AD1⊥DP,
又因为l∥AD1,所以l⊥DP,故B正确;
对于C,如图3,连接BC1,AD1,当P为B1C的中点时,过点A,P,D1的平面为平面ABC1D1,当点P从B1C的中点向点B1运动时,截面过平面ADD1A1,AA1B1B,BCC1B1,A1B1C1D1,当点P从B1C的中点向点C运动时,截面过平面ADD1A1,ABCD,BCC1B1,DCC1D1,则过点A,P,D1的平面最多与正方体的四个面相交,所以截面图形最多为四边形,故C错误;
图3
对于D,连接A1D,AD1,且A1D与AD1相交于点E,则E为A1D的中点,
所以在△A1DD1中,E到各顶点的距离相等,过E作EF⊥平面A1DD1,交B1C于F,则球心O一定在EF上,且OA1=OP,
设球的半径为r,由题意可得A1D=a,
当点P与点F重合时,a-a,此时r最小;
当点P与点B1或点C重合时,△A1EO≌△B1FO,
所以r=a,此时r最大.
所以三棱锥P-A1DD1的外接球的半径的取值范围是,故D正确.故选ABD.
11.ABC 取A1D的中点N,连接MN,EN,易证四边形BMNE是平行四边形,所以BM∥EN,因为BM 平面A1DE,EN 平面A1DE,所以BM∥平面A1DE,故A正确;
易知DN=,∠A1DE=∠ADE=45°,
在△DEN中,根据余弦定理得EN2=,故B正确;
连接EC,因为M为A1C的中点,所以=2=2,
故=S△CDE·h,其中h表示A1到平面ABCD的距离,当平面A1DE⊥平面ABCD时,h达到最大值,此时,故C正确;
假设平面A1DE⊥平面A1CD,又平面A1DE∩平面A1CD=A1D,A1E⊥A1D,A1E 平面A1DE,所以A1E⊥平面A1CD,所以A1E⊥A1C,
在Rt△A1CE中,A1E=1,EC=,所以A1C=1.
又因为A1D=1,CD=2,所以A1D+A1C=CD,故A1,C,D三点共线,
所以A1∈CD,得A1∈平面ABCD,与题干矛盾,故D不正确.故选ABC.
12.答案 112或72
解析 设正四棱柱的底面边长、侧棱长分别为a cm,l cm,
则
∴S棱柱侧=4×4×7=112(cm2)或S棱柱侧=4×6×3=72(cm2).
13.答案
解析 如图,连接BD,交AC于点O,连接OE,由四边形ABCD是正方形,得BO=OD,在线段PE上取点G,使得GE=ED,由PE=,
连接BG,FG,则BG∥OE,由OE 平面ACE,BG 平面ACE,
得BG∥平面ACE,而BF∥平面ACE,BG∩BF=B,BG,BF 平面BGF,
因此平面BGF∥平面ACE,又平面PCD∩平面ACE=EC,平面PCD∩平面BGF=GF,则GF∥EC,所以λ=.
14.答案 3;
解析 因为EF∥平面BCD,EF 平面ABC,平面ABC∩平面BCD=BC,所以EF∥BC,
因为正四面体ABCD的每个面都是等边三角形,所以△AEF也为等边三角形,所以AB=BE+AE=1+2=3.
该球球面与正四面体的四个面都相交,所得的交线分为两类:一类是球面与三个侧面ABD,ABC,ACD的交线,与侧面ABC的交线为,,
又AB=3,∠BAC=60°,
所以,
球面与侧面ABD,ACD的交线与一样长,
另一类是球面与底面BCD的交线,过D作DP⊥BC,垂足为P,过A作AO⊥DP,垂足为O,则OD=,
所以AO=,故球面与底面BCD刚好相交于底面BCD各边的中点处,此时形成的交线是底面BCD的内切圆,
则内切圆半径为OP=,
故内切圆的周长为2π×π,
因此所有的交线长为3×.
15.证明 (1)如图,连接AD1,EF,BC1.
因为BC=CC1,CE=CF,所以,所以EF∥BC1.(3分)
由长方体的性质可知AD1∥BC1,所以AD1∥EF.
所以A,D1,E,F四点共面.(6分)
(2)由(1)可得AD1∥EF,AD1≠EF,则四边形AEFD1是梯形,
故直线AE与直线D1F必相交,记AE∩D1F=P.(8分)
因为P∈AE,且AE 平面ABCD,所以P∈平面ABCD,
因为P∈D1F,且D1F 平面CDD1C1,所以P∈平面CDD1C1.(10分)
因为平面ABCD∩平面CDD1C1=CD,所以P∈CD,
即直线AE,D1F,DC交于一点.(13分)
16.解析 (1)如图,分别取AB,DE的中点G,H,连接CG,FH,HG,则截面CFHG即为所求.
(3分)
理由如下:
因为AD,BE,CF均垂直于平面ABC,所以AD∥BE∥CF,
因为AD=2,BE=4,所以四边形ABED为梯形.
又G,H分别为AB,DE的中点,所以HG∥BE,HG=3,
所以HG∥CF,HG=CF,所以四边形CFHG为平行四边形.
因为AC=BC,G为AB的中点,所以CG⊥AB.
因为AD⊥平面ABC,CG 平面ABC,所以AD⊥CG.(5分)
因为AB∩AD=A,所以CG⊥平面ABED,又CG 平面CFHG,所以平面CFHG⊥平面ABED,所以截面CFHG即为所求.(6分)
(2)解法一:如图,过点A作AM⊥BC,交BC的延长线于点M.
因为BE⊥平面ABC,AM 平面ABC,所以BE⊥AM,
又BC∩BE=B,BC,BE 平面BCFE,所以AM⊥平面BCFE.(9分)
在△ABC中,AC=BC,∠ACB=120°,AB=4,易得AC=BC=4,
所以S△ABC=.
因为AM=AC·sin60°=4×,
所以VD-BCFE=,(11分)
VD-ABC=,(13分)
所以V多面体ABCDEF=VD-ABC+VD-BCFE=.(15分)
解法二:如图,将多面体ABCDEF补成直三棱柱ABC-A'B'C',
其中A'D=4,B'E=2,C'F=3,AA'=6,
则V多面体ABCDEF=VABC-A'B'C',(9分)
在△ABC中,AC=BC,∠ACB=120°,AB=4,易得AC=BC=4,
所以S△ABC=,(13分)
所以VABC-A'B'C'=S△ABC·AA'=4,
所以V多面体ABCDEF=12.(15分)
解法三:如图,在多面体ABCDEF中作直三棱柱ABC-DPQ,
则V多面体ABCDEF=VABC-DPQ+VD-EFQP,(9分)
过点A作AM⊥BC,交BC的延长线于点M,
因为BE⊥平面ABC,AM 平面ABC,所以BE⊥AM,
又BC∩BE=B,BC,BE 平面BCFE,所以AM⊥平面BCFE.
在△ABC中,AC=BC,∠ACB=120°,AB=4,易得AC=BC=4,
所以S△ABC=,(12分)
因为AM=AC·sin60°=4×,
所以VABC-DPQ=S△ABC·AD=4,
VD-EFQP=,
所以V多面体ABCDEF=VABC-DPQ+VD-EFQP=8.(15分)
17.解析 (1)证明:取BD的中点E,连接AE,CE,因为AB=AD=BC=CD,所以BD⊥CE,BD⊥AE,(2分)
因为AE∩CE=E,AE,CE 平面ACE,所以BD⊥平面ACE,
因为AC 平面ACE,所以AC⊥BD.(4分)
(2)因为AB=AC=AD=BC=CD=a,BD=a,
又AE2+CE2=a2=a2=AC2,所以△ACE为等腰直角三角形,且AE⊥CE,(6分)
又AE⊥BD,BD∩CE=E,BD,CE 平面BCD,所以AE⊥平面BCD,
所以直线AC与平面BCD所成的角为∠ACE,(8分)
在Rt△AEC中,AE=CE,
所以∠ACE=45°,所以直线AC与平面BCD所成的角为45°.(9分)
(3)取BC的中点F,连接AF,EF,则EF∥CD,且EF=,(10分)
因为BC2+CD2=a2+a2=2a2=BD2,所以BC⊥CD,
所以BC⊥EF,(11分)
因为AB=AC=BC,所以BC⊥AF,
所以∠AFE是二面角A-BC-D的平面角,(13分)
在Rt△AEF中,tan∠AFE=,
即二面角A-BC-D的正切值为.(15分)
18.解析 (1)证明:在△AOC中,
因为OA=OC,D为AC的中点,所以AC⊥DO.
又PO垂直于圆O所在的平面,所以PO⊥AC.(2分)
因为DO∩PO=O,DO,PO 平面PDO,
所以AC⊥平面PDO.(4分)
(2)因为点C在圆O上,
所以当CO⊥AB时,C到AB的距离最大,且最大值为1.
又AB=2OB=2,所以△ABC面积的最大值为×2×1=1.(7分)
因为三棱锥P-ABC的高PO=1,
所以三棱锥P-ABC的体积的最大值为.(10分)
(3)在△POB中,PO=OB=1,∠POB=90°,
所以PB=,所以PB=PC=BC.
在三棱锥P-ABC中,将△BCP绕直线PB旋转至△BC'P,使之与△ABP共面,如图所示.
当O,E,C'共线时,CE+OE取得最小值.(14分)
因为OP=OB,C'P=C'B,所以OC'垂直平分PB,则E为PB的中点.
从而OC'=OE+EC'=,
即CE+OE的最小值为.(17分)
19.解析 (1)证明:因为PE⊥ED,PE⊥EB,
EB∩ED=E,EB,ED 平面EBCD,所以PE⊥平面EBCD,
因为BC 平面EBCD,所以PE⊥BC,
因为BC⊥EB,EB∩PE=E,EB,PE 平面PEB,
所以BC⊥平面PEB,(2分)
因为EM 平面PEB,所以BC⊥EM,
因为PE=EB,PM=MB,所以EM⊥PB,(4分)
因为BC∩PB=B,BC,PB 平面PBC,所以EM⊥平面PBC,
因为EM 平面EMN,所以平面EMN⊥平面PBC.(7分)
(2)假设存在点N满足题意,如图,过M作MQ⊥EB于Q,
因为PE⊥EB,所以PE∥MQ,
由(1)知,PE⊥平面EBCD,所以MQ⊥平面EBCD,
因为EN 平面EBCD,所以MQ⊥EN,(10分)
过Q作QR⊥EN于R,连接MR,
因为MQ∩QR=Q,MQ,QR 平面MQR,所以EN⊥平面MQR,
因为MR 平面MQR,所以EN⊥MR,
所以∠MRQ为二面角B-EN-M的平面角,(12分)
不妨设PE=EB=BC=2,则MQ=1,
在Rt△EBN中,设BN=x(0
所以tan∠MRQ=,又0
综上,存在点N,使得二面角B-EN-M的平面角的正切值为,此时N为BC的中点.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
