第三章 圆锥曲线的方程章末小结复习课 课件(共35张PPT)
文档属性
| 名称 | 第三章 圆锥曲线的方程章末小结复习课 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-10-17 11:10:21 | ||
图片预览











文档简介
(共35张PPT)
第三章 圆锥曲线的方程章末复习小结
人教A版(2019)
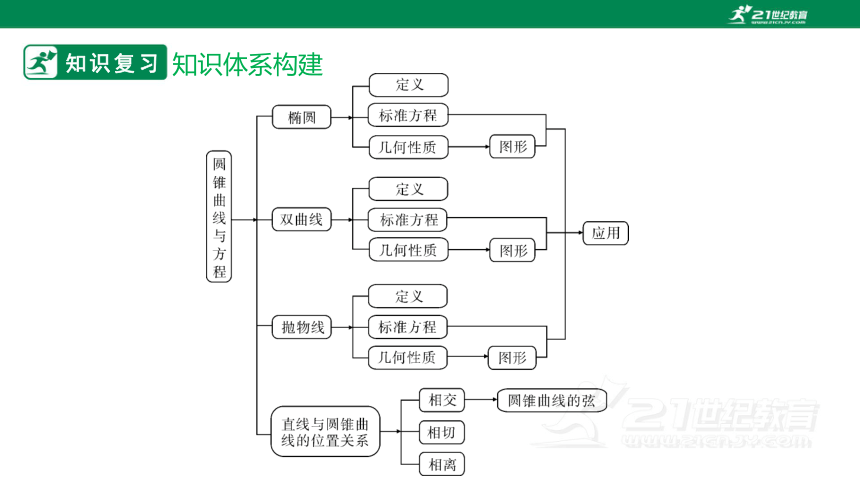
知识复习
知识体系构建
知识梳理
1.椭圆概念与简单几何性质
椭圆定义 椭圆标准方程
焦点坐标
半轴长 对称性 顶点坐标
a、b、c关系 离心率 图形
范围
把平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫做椭圆
(a>b>0).
(a>b>0).
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
关于x、y轴成轴对称;关于原点(0,0)成中心对称
A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
长半轴长为a,短半轴长为b(a>b).
A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)
a2=b2+c2(a>b>0).
e=, e∈(0,1).
F1
F2
M
x
y
O
F1
F2
M
x
y
O
-a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
知识梳理
2.双曲线的概念与简单几何性质
双曲线定义 标准方程
图像
焦点
顶点
范围
对称性 虚实轴 离心率 渐近线
F1(-c,0)
F2(c,0)
.
.
y
B2
A1
A2
B1
x
O
F2(0,c)
F1(0,-c)
x
B1
y
O
.
B2
A1
A2
.
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
x≤-a或x≥a,y∈R
y≤-a或y≥a,x∈R
对称轴:x轴、y轴;中心:原点
实轴长:2a;虚轴长:2b
e=∈(1,+∞),c2=a2+b2
.
.
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹
)
)
知识梳理
3.抛物线的概念与简单几何性质
抛物线定义 图形
标准方程
焦点坐标
准线
顶点坐标 对称轴 离心率 范围
把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
F(,0)
F(,0)
F(0,)
F(0,)
x=-.
x=.
y=-.
y=.
(0,0)
x轴
y轴
e=1
x≥0,y∈R
x≤0,y∈R
y≥0,x∈R
y≤0,x∈R
题型探究
【例1】⑴若命题甲:动点P到两定点A,B的距离之和|PA|+|PB|=2a(a>0,a是常数);命题乙:点P的轨迹是椭圆,则甲是乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
⑵平面内有两个定点F1(-5,0)和F2(5,0),动点P满足|PF1|-|PF2|=6,则动点P的轨迹方程是 .
解:
⑴若点P的轨迹是椭圆,则一定有|PA|+|PB|=2a(a>0);
∴甲是乙的必要不充分条件.故选B.
题型1:圆锥曲线的定义
反过来,若|PA|+|PB|=2a(a>0),则点P的轨迹可能是线段,也可能不存在.
⑵|PF1|-|PF2|=6<|F1F2|=10,根据双曲线的定义可知点P的轨迹为双曲线的右支,且a=3,c=5,
∴b2=16,
故轨迹方程为(x≥3).
B
(x≥3)
初试身手
1.已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N. 若M为FN的中点, 则|FN|=_______.
解:
如图,过M、N分别作抛物线准线的垂线,垂足分别为M1、N1,设抛物线的准线与x轴的交点为F1,则|NN1|=|OF1|=2,|FF1|=4.
∴|MM1|=3,
由抛物线的定义知|FM|=|MM1|=3,
∵M为FN的中点,
6
∴|FN|=2|FM|=6.
题型探究
【例2】⑴已知双曲线C: =1(a>0,b>0)的一条渐近线方程为y= x,且与椭圆+ =1有公共焦点,则C的方程为( )
A. =1 B. =1 C. =1 D. =1
解:
⑴由双曲线的渐近线方程可设双曲线方程为=k(k>0),即=1,
则由题意知,点A关于点P的对称点B(-a,2a-6)在l2上,
∵双曲线与椭圆+=1有公共焦点,
题型2:圆锥曲线的标准方程
∴4k+5k=12-3,解得k=1,
故双曲线C的方程为=1.
B
题型探究
【例2】⑵已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与C交于A,B两点. 若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( )
A. +y2=1 B. +=1 C. +=1 D.+=1
解:
⑵设|F2B|=x(x>0),则|AF2|=2x,|AB|=3x,|BF1|=3x,|AF1|=4a-(|AB|+|BF1|)=4a-6x,
由椭圆的定义知|BF1|+|BF2|=2a=4x,
∴|AF1|=2x,
题型2:圆锥曲线的标准方程
即4x2=4x2+22+8x·cos∠BF2F1 ②,
在△BF1F2中,由余弦定理得|BF1|2=|BF2|2+|F1F2|2-2|F2B|·|F1F2|cos∠BF2F1,
即9x2=x2+22-4x·cos∠BF2F1 ①,
在△AF1F2中,由余弦定理可得|AF1|2=|AF2|2+|F1F2|2-2|AF2|·|F1F2|cos∠AF2F1,
由①②得x=,所以2a=4x=2,a=,所以b2=a2-c2=2.
所以椭圆的方程为+=1.故选B.
B
初试身手
2.⑴已知椭圆的中心在原点,焦点在x轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( )
A. B. C. D.
解:
⑴∵2a=18,2c=×2a=6,
∴a=9,c=3,b2=81-9=72.
∴所求方程为.故选A.
A
初试身手
2.⑵已知双曲线C:(a>0,b>0)的一条渐近线方程为y=x,且与椭圆有公共焦点,则C的方程为( )
A. B. C. D.
解:
⑵根据双曲线C的渐近线方程为y=,
可知. ①
又椭圆的焦点坐标为(3,0)和(-3,0),
∴a2+b2=9. ②
根据①②可知a2=4,b2=5,
∴C的方程为.故选B.
B
题型探究
【例3】⑴双曲线=1(a>0,b>0)的离心率为,则其渐近线方程为( )
A. y=±x B. y=± x C. y=± x D. y=± x
题型3:圆锥曲线的简单几何性质
解:
⑴∵e=,
∴,
∴双曲线的渐近线方程为y=± x=±x.故选A.
A
题型探究
【例3】⑵已知F1,F2是椭圆C: =1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A且斜率为的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为( )
A. B. C. D.
题型3:圆锥曲线的简单几何性质
解:
⑵由题意可得直线AP的方程为y= (x+a),①
直线PF2的方程为y= (x-c).②
如图,过P向x轴引垂线,垂足为H,则PH= (a+c).
联立①②得y= (a+c),
∵∠PF2H=60°, PF2=F1F2=2c, PH= (a+c),
∴sin 60°= , 即a+c=5c, 即a=4c,
∴e= .故选D.
D
题型探究
【例2】⑶(多选)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点A(0,2),则C的方程为( )
A.y2=4x B.y2=8x C.y2=2x D.y2=16x
解:
⑵由已知得抛物线的焦点F(,0),设点M(x0,y0),
则,
题型3:圆锥曲线的简单几何性质
,
由已知得
即,y0=4,M(,4),
由|MF|=5,得
又p>0,解得p=2或p=8.
∴C的方程为y2=4x或y2=16x.故选AD.
AD
初试身手
解:
3.⑴设F为双曲线C: =1(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P,Q两点.若|PQ|=|OF|,则C的离心率为( )
A. B. C.2 D.
⑴∵|PQ|=|OF|=c,
∴P .
∴PQ过点.
∴a2= ,
又∵|OP|=a,
∴ =2, e= .故选A.
A
初试身手
解:
3.⑵已知椭圆(a>b>0)的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若,则该椭圆的离心率的取值范围为 .
⑵∵A(-a,0),B(0,b),M(),F(c,0),
∴,
又,
∴结合0<e<1,得0<e≤-1.
∴2a2-2ac-c2≥0,即e2+2e-2≤0,
0<e≤-1
初试身手
解:
3.⑶(多选)已知抛物线C:y2=2px(p>0)的焦点为F,直线l的斜率为且经过点F,直线l与抛物线C交于A,B两点(点A在第一象限),与抛物线的准线交于点D,若|AF|=4,则以下结论正确的是 ( )
A.p=2 B.F为AD中点 C.|BD|=2|BF| D.|BF|=2.
⑵如图,F(,0),直线l的斜率为,则
联立,得12x2-20px+3p2=0,
由|AF|==4,得p=2,
∴抛物线方程为y2=4x.
直线方程为y=(x-),
解得,
初试身手
解:
3.⑶(多选)已知抛物线C:y2=2px(p>0)的焦点为F,直线l的斜率为且经过点F,直线l与抛物线C交于A,B两点(点A在第一象限),与抛物线的准线交于点D,若|AF|=4,则以下结论正确的是( )
A.p=2 B.F为AD中点 C.|BD|=2|BF| D.|BF|=2.
∴,|BF|=,
|BD|+|BF|==4,则F为AD中点,
故选ABC.
∴抛物线方程为y2=4x.
|BD|=,|BD|=2|BF|.
ABC
题型探究
【例4】已知椭圆(a>b>0)的一个顶点为A(0,1),离心率为,过点B(0,-2)及左焦点F1的直线交椭圆于C,D两点,右焦点为F2.
⑴求椭圆的方程;
⑵求弦长|CD|.
题型4:直线与圆锥曲线的位置关系
解:
⑴∵椭圆(a>b>0)的一个顶点为A(0,1),
∴b=1,
又,a2=b2+c2,
∴a2=2,c=1.
∴椭圆的方程为.
⑵设C(x1,y1),D(x2,y2),
椭圆的左焦点F1(-1,0),所以直线BF1的方程为,即y=-2x-2,
联立,得9x2+16x+6=0,
题型探究
【例4】已知椭圆(a>b>0)的一个顶点为A(0,1),离心率为,过点B(0,-2)及左焦点F1的直线交椭圆于C,D两点,右焦点为F2.
⑴求椭圆的方程;
⑵求弦长|CD|.
题型4:直线与圆锥曲线的位置关系
解:
∴x1+x2=-,x1x2=,
=.
∴|CD|=.
联立,得9x2+16x+6=0,
题型探究
【例5】已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.
⑴若|AF|+|BF|=4, 求l的方程;
∴|AF|+|BF|=x1+x2+ ,
⑴由题设得F ,
设直线l:y= x+t, A(x1,y1), B(x2,y2).
题型4:直线与圆锥曲线的位置关系
由 可得9x2+12(t-1)x+4t2=0,
解:
由题设可得x1+x2=.
则x1+x2=- .
∴- = , 得t=- .
∴l的方程为y=x-.
题型探究
【例5】已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.
⑵若=3, 求|AB|
由,得y2-2y+2t=0.
⑵由=3可得y1=-3y2.
题型4:直线与圆锥曲线的位置关系
代入C的方程得x1=3, x2= .
解:
∴y1+y2=2.从而-3y2+y2=2,y2=-1, y1=3.
∴|AB|= .
初试身手
解:
4.已知椭圆C:(a>b>0)过点(1,),且焦距为2.
⑴求椭圆C的标准方程;
⑵设过点P(-2,0)的直线l与椭圆C交于不同的两点,求直线l的斜率k的取值范围.
⑴由2c=2得c=1,则a2=b2+c2=b2+1,
解得b2=1,a2=2,
⑵由题意设直线l的方程为y=k(x+2).
把(1,)代入椭圆C的方程,得,
∴故椭圆C的标准方程为.
当k=0时,显然满足题意.
当k≠0时,联立,整理得(1+2k2)x2+8k2x+8k2-2=0.
初试身手
解:
4.已知椭圆C:(a>b>0)过点(1,),且焦距为2.
⑴求椭圆C的标准方程;
⑵设过点P(-2,0)的直线l与椭圆C交于不同的两点,求直线l的斜率k的取值范围.
由Δ=(8k2)2-4(1+2k2)(8k2-2)>0,
解得,
∴斜率k的取值范围为.
当k≠0时,联立,整理得(1+2k2)x2+8k2x+8k2-2=0.
初试身手
解:
5.知抛物线C:y2=4x的焦点为F,过F的直线与C交于A、B两点,且线段AB中点的纵坐标为2,O为坐标原点,则△AOB的面积为( )
A.2 B. C.2 D.4
方法1:设直线AB的方程为x=ty+1, A(x1,y1), B(x2,y2), 线段AB的中点为M,
∴y1+y2=4t,y1y2=-4,
由yM= =2t=2, 得t=1,
由,消去x得y2-4ty-4=0,
A
∴S△AOB= |OF||y1-y2|= =2.故选A.
初试身手
解:
5.知抛物线C:y2=4x的焦点为F,过F的直线与C交于A、B两点,且线段AB中点的纵坐标为2,O为坐标原点,则△AOB的面积为( )
A.2 B. C.2 D.4
方法2:设A(x1,y1), B(x2,y2).
∴直线AB的方程为y=x-1,
由抛物线定义可得|AB|=x1+x2+2=y1+y2+4=8,
由,得kAB= = =1,
A
∴S△AOB= |AB|d=2.故选A.
而点O到直线AB的距离d= ,
题型探究
【例6】已知点P()是椭圆C:(a>b>0)上一点,A,B分别为椭圆C的左、右顶点,直线l过椭圆C的右焦点F,且点A,B到直线l的距离的比值为3.
⑴求椭圆C的标准方程;
题型5:圆锥曲线中的证明问题
⑴由点P()在椭圆C:(a>b>0)上,得 ①,
设F(c,0),由点A,B到直线l的距离的比值为3得|AF|=3|BF|,即a+c=3(a-c),a=2c,
∴a2=4c2=4a2-4b2,即3a2=4b2 ②
由①②得a2=4,b2=3,
∴椭圆C的标准方程为.
解:
题型探究
【例6】已知点P()是椭圆C:(a>b>0)上一点,A,B分别为椭圆C的左、右顶点,直线l过椭圆C的右焦点F,且点A,B到直线l的距离的比值为3.
⑵若点Q是直线x=4上且不在x轴上的动点,直线AQ,BQ分别与椭圆C交于另一点M,N,求证:M,F,N三点共线.
题型5:圆锥曲线中的证明问题
⑵由⑴知F(1,0),A(-2,0),B(2,0),
易知直线MN的斜率不为0,设直线MN的方程为x=my+t,
代入,得(3m2+4)y2+6tmy+3t2-12=0,
∴Δ=48(3m2-t2+4)>0,
设M(x1,y1),(x2,y2),(4,y0)(y0≠0),
解:
∴,
题型探究
【例6】已知点P()是椭圆C:(a>b>0)上一点,A,B分别为椭圆C的左、右顶点,直线l过椭圆C的右焦点F,且点A,B到直线l的距离的比值为3.
⑵若点Q是直线x=4上且不在x轴上的动点,直线AQ,BQ分别与椭圆C交于另一点M,N,求证:M,F,N三点共线.
题型5:圆锥曲线中的证明问题
由A,M,Q三点共线得,即,
由B,N,Q三点共线得,
∴=3,
∴t=1,直线MN的方程为x=my+1,
解:
∴直线MN的过点F,则M,F,N三点共线.
初试身手
解:
⑴∵, ∴,
∴a2=5,.
⑵证明:由⑴可知直线,点F2(3,0),
设P(,t),Q(x0,y0),则,
∵,
∴,
即.
6.已知双曲线E:(a>0)的中心为原点O,左、右焦点分别为F1,F2,离心率为,点P是直线x=上任意一点,点Q在双曲线E上,且满足.
⑴求实数a的值;
⑵证明:直线PQ与直线OQ的斜率之积是定值.
初试身手
解:
∵点Q(x0,y0)在双曲线E上,
∴,即,
∴,
∴直线PQ与直线OQ的斜率之积是定值.
即.
6.已知双曲线E:(a>0)的中心为原点O,左、右焦点分别为F1,F2,离心率为,点P是直线x=上任意一点,点Q在双曲线E上,且满足.
⑴求实数a的值;
⑵证明:直线PQ与直线OQ的斜率之积是定值.
作业布置
作业: p145 复习参考题3 第2,4,6,7,8,9题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第三章 圆锥曲线的方程章末复习小结
人教A版(2019)
知识复习
知识体系构建
知识梳理
1.椭圆概念与简单几何性质
椭圆定义 椭圆标准方程
焦点坐标
半轴长 对称性 顶点坐标
a、b、c关系 离心率 图形
范围
把平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫做椭圆
(a>b>0).
(a>b>0).
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
关于x、y轴成轴对称;关于原点(0,0)成中心对称
A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
长半轴长为a,短半轴长为b(a>b).
A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)
a2=b2+c2(a>b>0).
e=, e∈(0,1).
F1
F2
M
x
y
O
F1
F2
M
x
y
O
-a≤x≤a且-b≤y≤b
-b≤x≤b且-a≤y≤a
知识梳理
2.双曲线的概念与简单几何性质
双曲线定义 标准方程
图像
焦点
顶点
范围
对称性 虚实轴 离心率 渐近线
F1(-c,0)
F2(c,0)
.
.
y
B2
A1
A2
B1
x
O
F2(0,c)
F1(0,-c)
x
B1
y
O
.
B2
A1
A2
.
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
x≤-a或x≥a,y∈R
y≤-a或y≥a,x∈R
对称轴:x轴、y轴;中心:原点
实轴长:2a;虚轴长:2b
e=∈(1,+∞),c2=a2+b2
.
.
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹
)
)
知识梳理
3.抛物线的概念与简单几何性质
抛物线定义 图形
标准方程
焦点坐标
准线
顶点坐标 对称轴 离心率 范围
把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹
y2=2px(p>0)
y2=-2px(p>0)
x2=2py(p>0)
x2=-2py(p>0)
F(,0)
F(,0)
F(0,)
F(0,)
x=-.
x=.
y=-.
y=.
(0,0)
x轴
y轴
e=1
x≥0,y∈R
x≤0,y∈R
y≥0,x∈R
y≤0,x∈R
题型探究
【例1】⑴若命题甲:动点P到两定点A,B的距离之和|PA|+|PB|=2a(a>0,a是常数);命题乙:点P的轨迹是椭圆,则甲是乙的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
⑵平面内有两个定点F1(-5,0)和F2(5,0),动点P满足|PF1|-|PF2|=6,则动点P的轨迹方程是 .
解:
⑴若点P的轨迹是椭圆,则一定有|PA|+|PB|=2a(a>0);
∴甲是乙的必要不充分条件.故选B.
题型1:圆锥曲线的定义
反过来,若|PA|+|PB|=2a(a>0),则点P的轨迹可能是线段,也可能不存在.
⑵|PF1|-|PF2|=6<|F1F2|=10,根据双曲线的定义可知点P的轨迹为双曲线的右支,且a=3,c=5,
∴b2=16,
故轨迹方程为(x≥3).
B
(x≥3)
初试身手
1.已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N. 若M为FN的中点, 则|FN|=_______.
解:
如图,过M、N分别作抛物线准线的垂线,垂足分别为M1、N1,设抛物线的准线与x轴的交点为F1,则|NN1|=|OF1|=2,|FF1|=4.
∴|MM1|=3,
由抛物线的定义知|FM|=|MM1|=3,
∵M为FN的中点,
6
∴|FN|=2|FM|=6.
题型探究
【例2】⑴已知双曲线C: =1(a>0,b>0)的一条渐近线方程为y= x,且与椭圆+ =1有公共焦点,则C的方程为( )
A. =1 B. =1 C. =1 D. =1
解:
⑴由双曲线的渐近线方程可设双曲线方程为=k(k>0),即=1,
则由题意知,点A关于点P的对称点B(-a,2a-6)在l2上,
∵双曲线与椭圆+=1有公共焦点,
题型2:圆锥曲线的标准方程
∴4k+5k=12-3,解得k=1,
故双曲线C的方程为=1.
B
题型探究
【例2】⑵已知椭圆C的焦点为F1(-1,0),F2(1,0),过F2的直线与C交于A,B两点. 若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( )
A. +y2=1 B. +=1 C. +=1 D.+=1
解:
⑵设|F2B|=x(x>0),则|AF2|=2x,|AB|=3x,|BF1|=3x,|AF1|=4a-(|AB|+|BF1|)=4a-6x,
由椭圆的定义知|BF1|+|BF2|=2a=4x,
∴|AF1|=2x,
题型2:圆锥曲线的标准方程
即4x2=4x2+22+8x·cos∠BF2F1 ②,
在△BF1F2中,由余弦定理得|BF1|2=|BF2|2+|F1F2|2-2|F2B|·|F1F2|cos∠BF2F1,
即9x2=x2+22-4x·cos∠BF2F1 ①,
在△AF1F2中,由余弦定理可得|AF1|2=|AF2|2+|F1F2|2-2|AF2|·|F1F2|cos∠AF2F1,
由①②得x=,所以2a=4x=2,a=,所以b2=a2-c2=2.
所以椭圆的方程为+=1.故选B.
B
初试身手
2.⑴已知椭圆的中心在原点,焦点在x轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( )
A. B. C. D.
解:
⑴∵2a=18,2c=×2a=6,
∴a=9,c=3,b2=81-9=72.
∴所求方程为.故选A.
A
初试身手
2.⑵已知双曲线C:(a>0,b>0)的一条渐近线方程为y=x,且与椭圆有公共焦点,则C的方程为( )
A. B. C. D.
解:
⑵根据双曲线C的渐近线方程为y=,
可知. ①
又椭圆的焦点坐标为(3,0)和(-3,0),
∴a2+b2=9. ②
根据①②可知a2=4,b2=5,
∴C的方程为.故选B.
B
题型探究
【例3】⑴双曲线=1(a>0,b>0)的离心率为,则其渐近线方程为( )
A. y=±x B. y=± x C. y=± x D. y=± x
题型3:圆锥曲线的简单几何性质
解:
⑴∵e=,
∴,
∴双曲线的渐近线方程为y=± x=±x.故选A.
A
题型探究
【例3】⑵已知F1,F2是椭圆C: =1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A且斜率为的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为( )
A. B. C. D.
题型3:圆锥曲线的简单几何性质
解:
⑵由题意可得直线AP的方程为y= (x+a),①
直线PF2的方程为y= (x-c).②
如图,过P向x轴引垂线,垂足为H,则PH= (a+c).
联立①②得y= (a+c),
∵∠PF2H=60°, PF2=F1F2=2c, PH= (a+c),
∴sin 60°= , 即a+c=5c, 即a=4c,
∴e= .故选D.
D
题型探究
【例2】⑶(多选)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点A(0,2),则C的方程为( )
A.y2=4x B.y2=8x C.y2=2x D.y2=16x
解:
⑵由已知得抛物线的焦点F(,0),设点M(x0,y0),
则,
题型3:圆锥曲线的简单几何性质
,
由已知得
即,y0=4,M(,4),
由|MF|=5,得
又p>0,解得p=2或p=8.
∴C的方程为y2=4x或y2=16x.故选AD.
AD
初试身手
解:
3.⑴设F为双曲线C: =1(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P,Q两点.若|PQ|=|OF|,则C的离心率为( )
A. B. C.2 D.
⑴∵|PQ|=|OF|=c,
∴P .
∴PQ过点.
∴a2= ,
又∵|OP|=a,
∴ =2, e= .故选A.
A
初试身手
解:
3.⑵已知椭圆(a>b>0)的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若,则该椭圆的离心率的取值范围为 .
⑵∵A(-a,0),B(0,b),M(),F(c,0),
∴,
又,
∴结合0<e<1,得0<e≤-1.
∴2a2-2ac-c2≥0,即e2+2e-2≤0,
0<e≤-1
初试身手
解:
3.⑶(多选)已知抛物线C:y2=2px(p>0)的焦点为F,直线l的斜率为且经过点F,直线l与抛物线C交于A,B两点(点A在第一象限),与抛物线的准线交于点D,若|AF|=4,则以下结论正确的是 ( )
A.p=2 B.F为AD中点 C.|BD|=2|BF| D.|BF|=2.
⑵如图,F(,0),直线l的斜率为,则
联立,得12x2-20px+3p2=0,
由|AF|==4,得p=2,
∴抛物线方程为y2=4x.
直线方程为y=(x-),
解得,
初试身手
解:
3.⑶(多选)已知抛物线C:y2=2px(p>0)的焦点为F,直线l的斜率为且经过点F,直线l与抛物线C交于A,B两点(点A在第一象限),与抛物线的准线交于点D,若|AF|=4,则以下结论正确的是( )
A.p=2 B.F为AD中点 C.|BD|=2|BF| D.|BF|=2.
∴,|BF|=,
|BD|+|BF|==4,则F为AD中点,
故选ABC.
∴抛物线方程为y2=4x.
|BD|=,|BD|=2|BF|.
ABC
题型探究
【例4】已知椭圆(a>b>0)的一个顶点为A(0,1),离心率为,过点B(0,-2)及左焦点F1的直线交椭圆于C,D两点,右焦点为F2.
⑴求椭圆的方程;
⑵求弦长|CD|.
题型4:直线与圆锥曲线的位置关系
解:
⑴∵椭圆(a>b>0)的一个顶点为A(0,1),
∴b=1,
又,a2=b2+c2,
∴a2=2,c=1.
∴椭圆的方程为.
⑵设C(x1,y1),D(x2,y2),
椭圆的左焦点F1(-1,0),所以直线BF1的方程为,即y=-2x-2,
联立,得9x2+16x+6=0,
题型探究
【例4】已知椭圆(a>b>0)的一个顶点为A(0,1),离心率为,过点B(0,-2)及左焦点F1的直线交椭圆于C,D两点,右焦点为F2.
⑴求椭圆的方程;
⑵求弦长|CD|.
题型4:直线与圆锥曲线的位置关系
解:
∴x1+x2=-,x1x2=,
=.
∴|CD|=.
联立,得9x2+16x+6=0,
题型探究
【例5】已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.
⑴若|AF|+|BF|=4, 求l的方程;
∴|AF|+|BF|=x1+x2+ ,
⑴由题设得F ,
设直线l:y= x+t, A(x1,y1), B(x2,y2).
题型4:直线与圆锥曲线的位置关系
由 可得9x2+12(t-1)x+4t2=0,
解:
由题设可得x1+x2=.
则x1+x2=- .
∴- = , 得t=- .
∴l的方程为y=x-.
题型探究
【例5】已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.
⑵若=3, 求|AB|
由,得y2-2y+2t=0.
⑵由=3可得y1=-3y2.
题型4:直线与圆锥曲线的位置关系
代入C的方程得x1=3, x2= .
解:
∴y1+y2=2.从而-3y2+y2=2,y2=-1, y1=3.
∴|AB|= .
初试身手
解:
4.已知椭圆C:(a>b>0)过点(1,),且焦距为2.
⑴求椭圆C的标准方程;
⑵设过点P(-2,0)的直线l与椭圆C交于不同的两点,求直线l的斜率k的取值范围.
⑴由2c=2得c=1,则a2=b2+c2=b2+1,
解得b2=1,a2=2,
⑵由题意设直线l的方程为y=k(x+2).
把(1,)代入椭圆C的方程,得,
∴故椭圆C的标准方程为.
当k=0时,显然满足题意.
当k≠0时,联立,整理得(1+2k2)x2+8k2x+8k2-2=0.
初试身手
解:
4.已知椭圆C:(a>b>0)过点(1,),且焦距为2.
⑴求椭圆C的标准方程;
⑵设过点P(-2,0)的直线l与椭圆C交于不同的两点,求直线l的斜率k的取值范围.
由Δ=(8k2)2-4(1+2k2)(8k2-2)>0,
解得,
∴斜率k的取值范围为.
当k≠0时,联立,整理得(1+2k2)x2+8k2x+8k2-2=0.
初试身手
解:
5.知抛物线C:y2=4x的焦点为F,过F的直线与C交于A、B两点,且线段AB中点的纵坐标为2,O为坐标原点,则△AOB的面积为( )
A.2 B. C.2 D.4
方法1:设直线AB的方程为x=ty+1, A(x1,y1), B(x2,y2), 线段AB的中点为M,
∴y1+y2=4t,y1y2=-4,
由yM= =2t=2, 得t=1,
由,消去x得y2-4ty-4=0,
A
∴S△AOB= |OF||y1-y2|= =2.故选A.
初试身手
解:
5.知抛物线C:y2=4x的焦点为F,过F的直线与C交于A、B两点,且线段AB中点的纵坐标为2,O为坐标原点,则△AOB的面积为( )
A.2 B. C.2 D.4
方法2:设A(x1,y1), B(x2,y2).
∴直线AB的方程为y=x-1,
由抛物线定义可得|AB|=x1+x2+2=y1+y2+4=8,
由,得kAB= = =1,
A
∴S△AOB= |AB|d=2.故选A.
而点O到直线AB的距离d= ,
题型探究
【例6】已知点P()是椭圆C:(a>b>0)上一点,A,B分别为椭圆C的左、右顶点,直线l过椭圆C的右焦点F,且点A,B到直线l的距离的比值为3.
⑴求椭圆C的标准方程;
题型5:圆锥曲线中的证明问题
⑴由点P()在椭圆C:(a>b>0)上,得 ①,
设F(c,0),由点A,B到直线l的距离的比值为3得|AF|=3|BF|,即a+c=3(a-c),a=2c,
∴a2=4c2=4a2-4b2,即3a2=4b2 ②
由①②得a2=4,b2=3,
∴椭圆C的标准方程为.
解:
题型探究
【例6】已知点P()是椭圆C:(a>b>0)上一点,A,B分别为椭圆C的左、右顶点,直线l过椭圆C的右焦点F,且点A,B到直线l的距离的比值为3.
⑵若点Q是直线x=4上且不在x轴上的动点,直线AQ,BQ分别与椭圆C交于另一点M,N,求证:M,F,N三点共线.
题型5:圆锥曲线中的证明问题
⑵由⑴知F(1,0),A(-2,0),B(2,0),
易知直线MN的斜率不为0,设直线MN的方程为x=my+t,
代入,得(3m2+4)y2+6tmy+3t2-12=0,
∴Δ=48(3m2-t2+4)>0,
设M(x1,y1),(x2,y2),(4,y0)(y0≠0),
解:
∴,
题型探究
【例6】已知点P()是椭圆C:(a>b>0)上一点,A,B分别为椭圆C的左、右顶点,直线l过椭圆C的右焦点F,且点A,B到直线l的距离的比值为3.
⑵若点Q是直线x=4上且不在x轴上的动点,直线AQ,BQ分别与椭圆C交于另一点M,N,求证:M,F,N三点共线.
题型5:圆锥曲线中的证明问题
由A,M,Q三点共线得,即,
由B,N,Q三点共线得,
∴=3,
∴t=1,直线MN的方程为x=my+1,
解:
∴直线MN的过点F,则M,F,N三点共线.
初试身手
解:
⑴∵, ∴,
∴a2=5,.
⑵证明:由⑴可知直线,点F2(3,0),
设P(,t),Q(x0,y0),则,
∵,
∴,
即.
6.已知双曲线E:(a>0)的中心为原点O,左、右焦点分别为F1,F2,离心率为,点P是直线x=上任意一点,点Q在双曲线E上,且满足.
⑴求实数a的值;
⑵证明:直线PQ与直线OQ的斜率之积是定值.
初试身手
解:
∵点Q(x0,y0)在双曲线E上,
∴,即,
∴,
∴直线PQ与直线OQ的斜率之积是定值.
即.
6.已知双曲线E:(a>0)的中心为原点O,左、右焦点分别为F1,F2,离心率为,点P是直线x=上任意一点,点Q在双曲线E上,且满足.
⑴求实数a的值;
⑵证明:直线PQ与直线OQ的斜率之积是定值.
作业布置
作业: p145 复习参考题3 第2,4,6,7,8,9题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
