第十三章 等腰三角形重难点突破(含解析) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十三章 等腰三角形重难点突破(含解析) 2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 09:34:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
等腰三角形重难点突破
知等腰(一) 等边对等角
类型一 知等腰求角度
1.如图,以点 A 为圆心画弧,交直线 l于B,C两点,再分别以 A,B为圆心大于 AB 长为半径画弧交于M,N 两点,直线MN 交直线l 于点D,若 ,则∠CAD 的度数为( )
A.20° B.25° C.30° D.40°
2.如图,∠AOB=10°,射线OA,OB 上有一系列点( 且满足O n.当时,n的值为( )
A.6 B.7 C.8 D.9
类型二 隐等腰求角度
3.如图,在△ABC 中,BF 平分 交AC于点F,E 是AF 的中点,DE⊥AC交AB 于点D,连接DC 交BF于点P,则 的度数是( )
A.36° B.54° C.72° D.90°
类型三 知等腰证全等
4.如图,在. 中, D 是 BC 的中点,E 是 AC 的中点,连接AD,BE.
(1)求证:
(2)连接DE,求证:
知等腰(二)“三线合一”直接用
类型一 等腰+角平分线
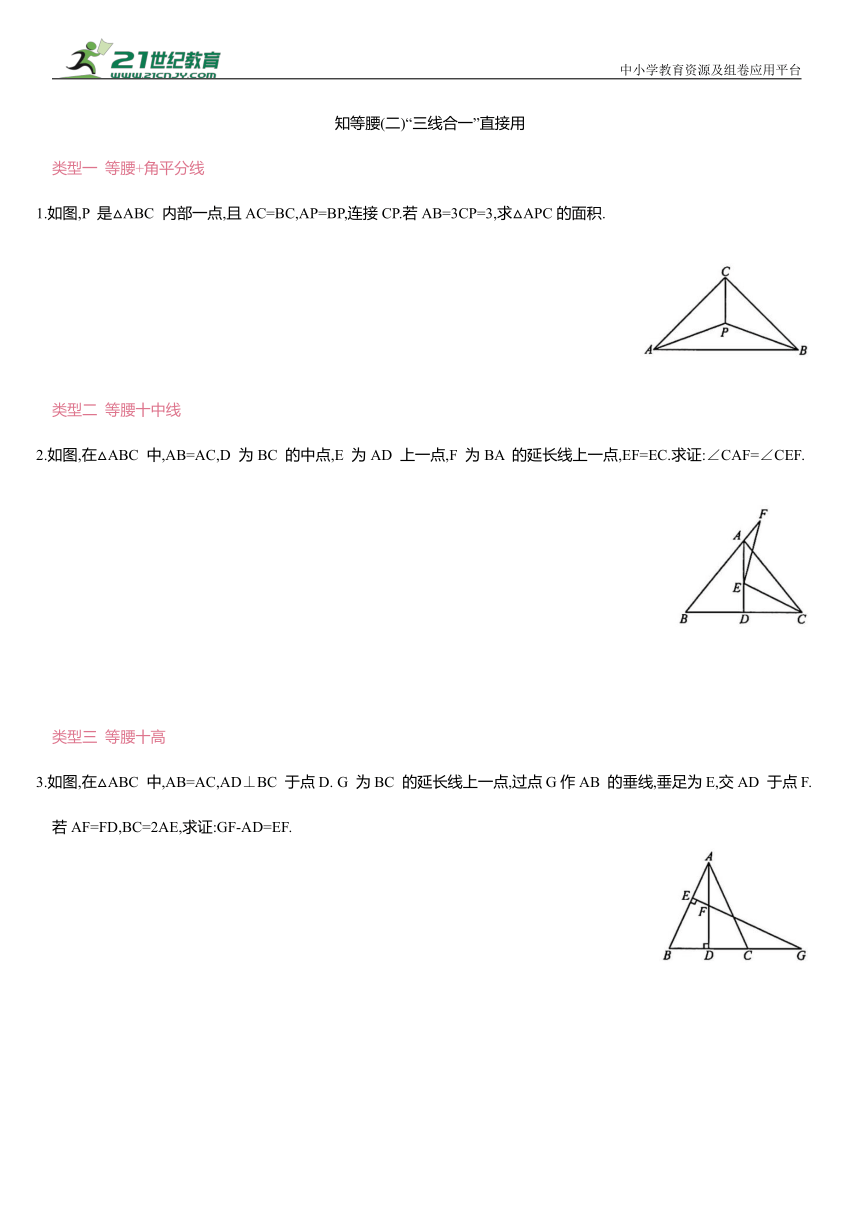
1.如图,P 是△ABC 内部一点,且AC=BC,AP=BP,连接CP.若AB=3CP=3,求△APC的面积.
类型二 等腰十中线
2.如图,在△ABC 中,AB=AC,D 为BC 的中点,E 为AD 上一点,F 为BA 的延长线上一点,EF=EC.求证:∠CAF=∠CEF.
类型三 等腰十高
3.如图,在△ABC 中,AB=AC,AD⊥BC 于点D. G 为BC 的延长线上一点,过点G作AB 的垂线,垂足为E,交AD 于点F.若AF=FD,BC=2AE,求证:GF-AD=EF.
知等腰(三)“三线合一”连接用
类型一 连中线得垂直
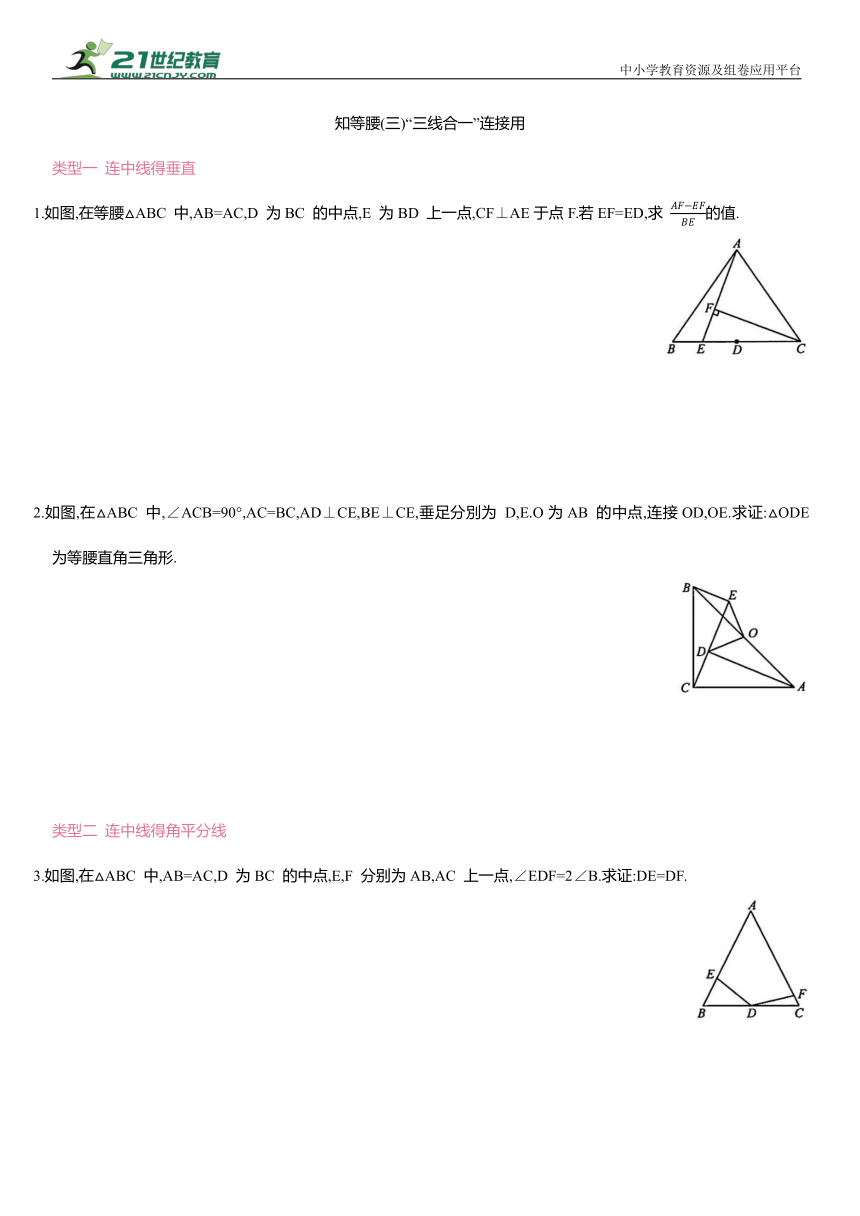
1.如图,在等腰△ABC 中,AB=AC,D 为BC 的中点,E 为BD 上一点,CF⊥AE于点F.若EF=ED,求 的值.
2.如图,在△ABC 中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分別为 D,E.O为AB 的中点,连接OD,OE.求证:△ODE 为等腰直角三角形.
类型二 连中线得角平分线
3.如图,在△ABC 中,AB=AC,D 为BC 的中点,E,F 分别为AB,AC 上一点,∠EDF=2∠B.求证:DE=DF.
知等腰(四)“三线合一”构造用
类型一 知等腰→作“三线”
1.如图,在△ABC 中,AB=AC,作等腰△ACD,使得AC=CD.若∠ACD 与∠BAC 互补,过点 C 作CH⊥AD 于点H,求证:
2.如图,在△ABC 中,CE⊥AC 交AB 于点E,D 为CE 的延长线上一点,点 B在CD 的垂直平分线上.若BE=AE,EC=1,则DE的长为 .
3.如图,在△ABC中,AB=AC,E 为边AC 上一点,过点 C 作 BC 的垂线,交BE 的延长线于点D,连接AD.若∠DAC=∠ABD,求证:AE=EC.
类型二 构等腰→用“三线”
4.如图,在△ABC中,AB=AC,D 为△ABC 外一点,AE⊥BD 于点 E,∠BDC=∠BAC,DE=3,CD=2,则BE的长为 .
知等腰(五) 方程思想求角
类型一 多等腰
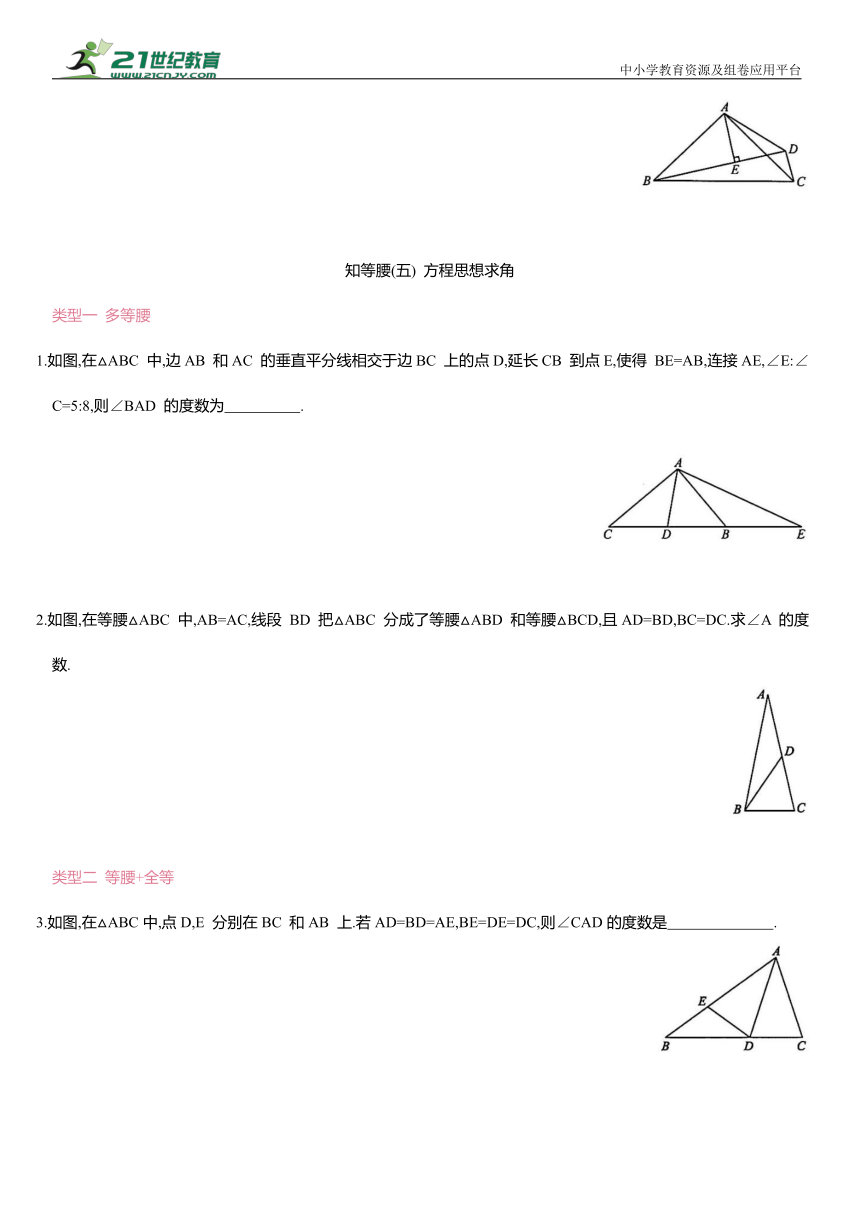
1.如图,在△ABC 中,边AB 和AC 的垂直平分线相交于边BC 上的点D,延长CB 到点E,使得 BE=AB,连接AE,∠E:∠C=5:8,则∠BAD 的度数为 .
2.如图,在等腰△ABC 中,AB=AC,线段 BD 把△ABC 分成了等腰△ABD 和等腰△BCD,且AD=BD,BC=DC.求∠A 的度数.
类型二 等腰+全等
3.如图,在△ABC中,点D,E 分别在BC 和AB 上.若AD=BD=AE,BE=DE=DC,则∠CAD的度数是 .
4.如图,在△ABC中,AD平分△ABC 的外角∠MAC,过点 C 作CE∥AB 交AD 于点E,点 F 在边AC上,且CF=AB.
(1)求证:EF=BC;
(2)若∠BCE=65°,∠AEF=2∠CEF,求∠BAC 的度数.
知等腰(六) 整体思想求角
类型一 共顶点三等腰
1如图,在四边形ABCD 中,AB=AC=AD,∠BAC=40°,则∠BDC 的度数为 .
2如图,点 D 在△ABC 内部,DB=DC,点E 在AB 上,DE 垂直平分AB.若∠ACB=75°,则∠BDE 的度数为 .
类型二 共底双等腰
3.如图,在△ABC 中,AB=AC,D 是△ABC 内部一点,DB=DC,E 是边AB上一点.若CD 平分∠ACE,∠AEC=100°,则∠BDC 的度数为 .
类型三 共顶点双等腰
4.如图,线段AB,DE 的垂直平分线交于点C,且∠ABC=∠CDE=78°,∠AEB=98°,则∠EBD 的度数为( )
A.162° B.152° C.122° D.112°
知等腰(七) 分类讨论求角
类型一 形状不明
1.在等腰△ABC中,AB=AC,两腰的垂直平分线交于点 P,已知∠BPC=90°,则等腰三角形的顶角度数为 .
2在△OPQ中,OP=OQ,OP 的垂直平分线交OP 于点D,交直线OQ于点E.若∠OEP=50°,则∠POQ的度数为 .
类型二 腰不明
3如图,在△ABC中,AB=BC,∠ABC=100°,AB 绕点B 顺时针旋转m°(0知等腰(八) 巧算面积
类型一 三角形面积→高底关联
1.如图,已知AC⊥BC,AC=BC,BE⊥CD 于点E,AD⊥CE 于点D.
(1)求证:DE=BE--AD;
(2)O为AB 的中点,连接OD,OE,若AD=4,ED=7,求△OEB 的面积.
2.如图,在四边形ABCD 中,∠ABC=∠CAB=∠ADC=45°,△ACD 面积为12,且CD 的长为6.求△BCD 的面积.
3.如图,在四边形ABCD 中,AB=AC=AD,AB⊥AC,AE⊥BD 于点E.若BD=10,AE=3,求△BCD 的面积.
类型二 多边形面积→割补计算
4.如图,在五边形ABCDE 中,∠AED=90°,BC=DE,连接AC,AD,且AB=AD,AC⊥BC,∠ABC=∠CAD,F 为BE 的中点.
(1)求证:AF⊥CD;
(2)若AE=6,DE=4,则五边形ABCDE 的面积为 .
5.如图,在四边形 ABCD 中,∠BAD+∠BCD═180°,点 E 在CD 上,点 F 在AD上,AB=AF,CB=CE,M为EF 的中点.
(1)求证:CM⊥AM;
(2)若CM=4,AM=6,求五边形ABCEF 的面积.
6.如图,在五边形ABCDE 中,∠EAB=∠EDC=90°,AB=AE,DC=DE,AE知等腰(九) 设参导角
类型一 设参得等角证垂直
1.如图,在△ABC中,AB=AC,点 E 在AB 上,以 BE 为底边作等腰△DBE,取 CE 的中点G,连接AG,DG.若BE≠AE,∠BDE+∠BAC=180°,求证:AG⊥DG.
类型二 设参导倍角证全等
2.如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 在边AC 上,点 E 在线段BD上,连接AE,且AE=BE,延长AE交BC于点F,过点A 作AG⊥AE,交BD 的延长线于点 G.
(1)求证:∠AGB=2∠GBC;
(2)若 D 是AC 的中点,求证:AF=AG.
突破 5 知等腰(一)等边对等角
1. C 解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°.
∵MN 为AB 的垂直平分线,
∴DA=DB,
∴∠BAD=∠ABC=70°,
∴∠CAD=∠BAD-∠BAC=30°.
故选 C.
2. D
3. D 解:连接DF.
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°.
∵BF 平分∠ABC,
∴∠ABF=∠FBC=36°,
∴∠BFC=∠BCF=72°.
∵AE=EF,DE⊥AF,
∴AD=DF,
∴∠DFE=36°,
∴∠DFP=72°,
∴∠DFB=∠CFB.
∵BF=BF,∠DBF=∠CBF,
∴△BDF≌△CBF,
∴BD=BC.
∵BF 平分∠ABC,
∴BP⊥CD,
∴∠BPD=90°.选 D.
4.证明:(1)∵AC=BC,
∴∠BAC=∠ABC.
∵D,E 分别为BC,AC的中点,
∴BD=DC=AE=EC.
∵AB=AB,
∴△ABE≌△BAD,
∴∠BAD=∠ABE;
(2)延长 DE 至点F,使 EF=DE.
∵∠AEF=∠DEC,AE=EC,
∴△AEF≌△CED,
∴AF=CD=BD,∠F=∠EDC,
∴AF∥CD,
∴∠FAD=∠ADB.
∵AD=DA,
∴△FAD≌△BDA,
∴AB=DF=2DE.
突破 6 知等腰(二)“三线合一”直接用
1.解: 在△ACP 和△BCP 中,AC=BC,AP=BP,CP=CP,
∴△ACP≌△BCP,
∴∠ACP=∠BCP.
延长 CP 交AB 于点 D.
∵∠ACP=∠BCP,AC=BC,
∵AB=3CP=3,即CP=1,
2.证明:过点 E 作 EG⊥AB 于点 G,EH⊥AC 于点 H.
∵AB=AC,D为BC的中点,
∴AD平分∠BAC.
∵EG⊥AB,EH⊥AC,
∴EG=EH,
∠EGF=∠EHC=90°.
∵EF=EC,
∴Rt△EGF≌Rt△EHC,
∴∠F=∠ACE,
∴∠CAF=∠CEF.
3.证明:过点 D 作 DH⊥GE 于点 H.
∵GE⊥AB,
∴∠FEA=∠DHF=90°.
∵∠AFE=∠DFH,AF=DF,
∴△AEF≌△DHF,
∴HF=EF,AE=DH.
∵AD⊥BC,AB=AC,
∴BD=CD,∠BAD=∠CAD.
∵BC=2AE,
∴AE=DH=CD.
∵∠AEF=∠GDF=90°,∠AFE=∠GFD,
∴∠BAD=∠CAD=∠G.
∵∠ADC=∠DHG=90°,
∴△DGH≌△ACD,
∴GH=AD,
∴GF- AD = GF-GH = HF =EF.
突破7 知等腰(三)“三线合一”连接用
1.解:连接AD.
∵AB=AC,D 为BC的中点,
∴AD⊥BC,BD=CD.
∵∠AED=∠CEF,EF=ED,
∴△AED≌△CEF,
∴AE=EC=ED+CD.
∵AE=AF+EF,EF=ED,
∴AF=CD=BD,
2.证明:连接 OC,设AB 与CE 交于点F.可证△ACD≌△CBE,
∴DC=EB.
∵AC=BC,∠ACB=90°,
∴∠ABC=∠BAC=45°.
∵O为AB 的中点,
∴CO⊥AB,
∴∠BCO=∠ABC,
∴OC=OB.
∵BE⊥CE,CO⊥AB,
∴∠BEC=∠BOC=90°.
又 ∵ ∠BFC = ∠BOC + ∠1 =∠BEC+∠2,
∴∠1=∠2,
∴△DCO≌△EBO,
∴DO=EO,∠BOE=∠COD.
∵∠COD+∠DOB=90°,
∴∠BOE+∠DOB=90°,
∴∠DOE=90°.
又∵DO=EO,
∴△ODE 为等腰直角三角形.
3.证明:连接 AD,过点 D 作DM⊥AB于点 M,作 DN⊥AC 于点 N.
∵AB=AC,D 为BC的中点,
∴AD平分∠BAC,∠B=∠C.
∵DM⊥AB,DN⊥AC,
∴DM=DN.
∵∠BAC+∠B+∠C=180°,
∴2∠B+∠BAC=180°.
∵∠EDF=2∠B,
∴∠EDF+∠BAC=180°,
180°.
∵∠AED+∠DEM=180°,
∴∠AFD=∠DEM.
∵∠DME=∠DNF=90°,
∴△DEM≌△DFN,
∴DE=DF.
突破 8 知等腰(四)“三线合一”构造用
1.证明:过点 A 作AE⊥BC 于点E.
∵AB=AC,
∵AC=CD,CH⊥AD,
∠CAH+∠ACH=90°.
∵∠BAC+∠ACD=180°,
∠ACD)=90°,
∴∠EAC=∠CAH.
∵CE⊥AE,CH⊥AH,
2.3 解:过点 B 作 BM⊥DC 于点 M.
∵AC⊥CD,
∴∠BME=∠ACE=90°.
∵∠BEM=∠AEC,BE=AE,
∴△BME≌△ACE(AAS),
∴ME=CE=1.
∵点 B 在 CD 的垂直平分线上,
∴BD=BC.
∵BM⊥CD,
∴DM=MC=ME+EC=2,
∴DE=DM+ME=3.
3.证明:过点 A 作 AF⊥BC,交 BD 于点 F.
∵AB=AC,
∴∠BAF=∠CAB.
∵AF⊥BC,CD⊥BC,
∴AF∥CD,
∴∠ACD=∠CAF=∠BAF.
在△ABF 和△CAD 中,
∴△ABF≌△CAD(ASA),
∴AF=CD.
又 AF∥CD,
∴△AFE≌△CDE(AAS),
∴AE=EC.
4.5 解:在BD 上截取BF=CD,连接AF.设 BD 与AC 相交于点G.
∵∠BDC=∠BAC,
∠DGC=∠AGB,
∴∠ACD=∠ABF.
∵AB=AC,BF=CD,
∴△ABF≌△ACD,
∴AF=AD.
∵AE⊥BD,
∴FE=DE=3.
∵BF=CD=2,
∴BE=BF+FE=5.
突破 9 知等腰(五)方程思想求角
1.50° 解:设∠E=5x,则∠C=8x.
∵BE=BA,
∴∠BAE=∠E=5x.
由题意,得AD=CD,AD=DB,
∴∠C=∠DAC=8x,
∠DAB=∠DBA=2∠E=10x,
∴8x+8x+10x+10x=180°,
∴∠BAD=10x=50°.
2.解:设∠A=x.
∵AD=BD,
∴∠A=∠ABD=x,
∴∠BDC=∠A+∠ABD=2x.
∵BC=DC,
∴∠BDC=∠CBD=2x,
∴∠ABC=∠ACB=3x,
∴3x+3x+x=180°,
3.36° 解:设∠B=x.
∵BE=ED,AD=BD=AE,
∴∠EDB=∠DAB=∠B=x,
∴∠ADC=2x=∠AED=∠ADE,
∴5x=180°,
∴x=36°.
可证△ADC≌△ADE,
∴∠CAD=∠BAD=36°.
4.解:(1)∵AD 平分∠MAC,CE∥MB,
∴∠CEA=∠MAD=∠CAD,
∴CE=CA.
∵AB∥CE,
∴∠BAC=∠ECF.
∵AB=CF,
∴△ABC≌△CFE,
∴EF=BC;
(2)设∠BAC=x,则∠ECF=x,
∴∠ACB=∠BCE-∠ECF=65°-x.
∵△ABC≌△CFE,
∴∠CEF=∠ACB=65°-x,
∴∠AEF=2∠CEF=2(65°-x),
∵∠ECF + ∠CEA + ∠CAE =180°,
180°,
∴x=42°,
∴∠BAC=42°.
突破 10知等腰(六)整体思想求角
1.20° 解:设∠ABD=x.
∵AC=AB=AD,∠BAC=40°,
∴∠ABC=∠ACB=70°,∠ADB=∠ABD=x,
∴∠CAD=∠BAD-∠BAC=140°—2x.
∵AC=AD,
∴∠ACD=∠ADC=20°+x,
∴∠BDC=∠ADC-∠ADB=20°.
2.75° 解:连接AD.
∵DE 垂直平分AB,
∴AD=BD.
∵DB=DC,
∴CD=AD=BD,
∴ ∠DBC = ∠DCB,∠DAC =∠DCA,∠DAB=∠DBA.
∵∠ACB=75°,
∴∠DCB + ∠DCA = ∠DBC +∠DAC=75°,
∴∠DCB + ∠DCA + ∠DBC +∠DAC=150°,
30°,
∵AD=BD,DE⊥AB,
3.80° 解:设∠ACD =∠DCE=x,∠ECB=y.
∵AB=AC,DB=DC,
∴∠ABC=∠ACB=2x+y,∠DCB=∠DBC=x+y.
∵∠AEC=∠ECB+∠EBC=2x+2y,
∴2x+2y=100°,
4. C 解:连接CE,则CD=CE,CA=CB,
∴∠BAC=∠ABC=78°,∠CED=∠CDE=78°,
∴∠ACB=∠ECD=24°,
∴∠ACE=∠BCD,
∴△ACE≌△BCD,
∴∠AEC=∠BDC.设∠CEB=x,则∠AEC=∠AEB--∠CEB=98°-x,
∴∠BED=∠CED--∠CEB=78°-x.
∵△ACE≌△BCD,
∴∠BDE=∠CDE-∠CDB=78°
故选 C.
突破 11 知等腰(七)分类讨论求角
1.45°或135° 解:①当△ABC 为锐角三角形时,如图1,连接AP.
∵AP=BP=CP,
∴∠BAP=∠ABP,
∠CAP=∠ACP,
∴易证∠BPC=∠BAP+∠CAP+∠ACP+∠ABP=2∠BAC=90°,
∴∠BAC=45°;
②当△ABC 为钝角三角形时,如图2,连接AP.
∵AP=BP=CP,
∴∠BAP=∠ABP,∠CAP=∠ACP,
∴∠BAP + ∠CAP + ∠ACP +∠ABP=2∠BAC.
∵∠PBA + ∠PCA + ∠PAB +∠PAC+∠BPC=360°,∠BPC=90°,
∴∠BAC=135°.
故答案为 45°或 135°.
2.65°或115° 解:①如图1,当△OPQ为锐角三角形时,
∵DE 垂直且平分OP,
∴∠ODE=∠PDE=90°,OE=PE,
又∵∠OEP=50°,
∴∠OED=∠PED=25°,
65°;
②如图2,当△OPQ 为钝角三角形时,
∵DE 垂直且平分OP,
∴∠ODE=∠PDE=90°,OE=PE,
又∵∠OEP=50°,
∴∠OED=∠PED=25°,
综上,∠POQ=65°或115°.
3.100°或 130°或 160°
解:(1)若AD=AC.
∵AB=AB,BD=BC,
∴△ABD≌△ABC,
∴∠ABD=∠ABC=100°,
∴m=∠ABD=100°;
(2)若AD=DC.
∵DB=DB,AB=BC,
∴△ABD≌△CBD,
∠ABC)=130°,
∴m=130°;
(3)若CD=CA.
∵CB=CB,BA=BD,
∴△CBD≌△CBA,
∴∠CBD=∠CBA=100°,
160°.
故 m 的值为 100°或130°或 160°.
突破 12 知等腰(八) 巧算面积
1.解:(1)∵AC⊥BC,AD⊥CD,BE⊥CD,
∴∠ACB=∠ADC=∠BEC=90°,
∴ ∠ACD + ∠BCE = ∠CBE +∠BCE=90°,
∴∠ACD=∠CBE.
∵AC=BC,
∴△ACD≌△CBE,
∴AD=CE,BE=CD,
∴DE=CD-CE=BE-AD;
(2)延长 DO 交 BE 于点 F.
∵∠CEB=90°,
∴AD∥BE,
∴∠DAO=∠FBO,∠ADO=∠BFO.
∵O为AB 的中点,
∴AO=BO,
∴△AOD≌△BOF,
∴BF=AD,DO=OF.
由(1)知AD=CE,
∴CE=BF.
∵BE=CD,
∴EF=DE=7,
∴EO⊥ DF,∠DEO = ∠FEO =
∵OE⊥DF,
∴∠EOF=90°,
∴∠OFE=45°,
∴∠OEF=∠OFE,
∴OE=OF.过点 O 作OM⊥EB 于点M,
∴∠EOM =∠FOM=45°,∠OEF
=∠EOM=∠FOM=∠OFM,
2.解:过点 B 作 BM⊥DC 交 DC 的延长线于点M,过点 A 作AN⊥CD 于点 N,
12,
∴AN=4.
∵AN⊥CD,∠ADC=45°,
∴DN=AN=4,
∴CN=CD--ND=2.
∵∠ABC=∠CAB=45°,
∴∠BCA=90°,
∴∠BCM+∠ACN=90°.
∵AN⊥CD,
∴∠ANC=90°,
∴∠CAN+∠ACN=90°,
∴∠BCM=∠CAN.
∵∠M=∠ANC=90°,
∴△BCM≌△CAN,
∴BM=CN=2,
=6.
3.解:过点C 分别作CF⊥AE,交 AE的延长线于点 F,作 CG⊥BD 于点G.
∵AB=AD,AE⊥BD,
∵AB = AC,AB⊥AC,∠BAE+∠CAF=∠CAF+∠ACF,
∴∠BAE=∠ACF,
∴△ABE≌△CAF,
∴BE=AF=5,
∴EF=AF-AE=2.
∵CF∥BD,
∴CG=EF=2,
4.解:(1)延长AF,BC交于点G.
∵AB = AD, ∠AED =∠ACB =90°,BC=DE,
∴△ABC≌△ADE,
∴∠BAC=∠DAE.
又∵∠ABC=∠CAD,
∴∠CAE = ∠CAD + ∠DAE =∠ABC+∠BAC=90°=∠ACB,
∴BG∥AE,
∴∠G=∠EAG.
∵EF=BF,∠AFE=∠GFB,
∴△AEF≌△GBF,
∴AE=BG.
∵AC=AE,
∴BG=AC.
∴△ABG≌△DAC,
∴∠G=∠ACD.
∵∠ACG=∠ACB=90°,即∠ACD+∠GCD=90°
∴∠G+∠GCD=90°,
∴AF⊥CD;
(2)由(1)可知,BG=AC=AE=6, =18.
∵△ABG≌△DAC,
∴S△ACD=18.
12,
S△ADE=12+18+12=42.
5.解:(1)延长 CM 至点 G,使 GM=CM,连接GF,AC,AG.
∵FM=EM,∠FMG=∠EMC,MG=MC,
∴△FGM≌△ECM,
∴∠GFM=∠CEM,FG=EC.
∵CB=CE,
∴FG=BC.在五边形 ABCEF 中,∠B+∠BAD+∠BCD+∠CEM+∠EFA=540°.
∵∠BAD+∠BCD=180°,
∴∠B+∠CEM+∠EFA=360°,
∴∠B+∠GFM+∠EFA=360°.
∵∠AFG + ∠GFM + ∠EFA =360°,
∴∠B=∠GFA.
∵AF=AB,
∴△ABC≌△AFG,
∴AG=AC.
∵CM=MG,
∴AM⊥CM;
(2)∵△FGM≌△ECM,△ABC≌△AFG,
6.4.5 解:取 BC 的中点F,连接 AF并延长至点 G,使 FG=AF,连接DF,CG,DG.
可证△AFB ≌△GFC,△AED≌△GCD,
另解过 B,C,E 三点,分别作 AD 的垂线段,证全等.
突破 13 知等腰(九) 设参导角
1.证明:设∠BAC=2x,则.
∵BD=DE,
∴∠ABD=∠DEB=x.
∵AB=AC,
延长 ED 交 BC 于点 F,延长 DG 至点 H,使 GH=DG,连接 AD,AH,HC.
∵DG=GH,∠EGD=∠CGH,EG=GC,
∴△EGD≌△CGH,
∴CH=DE=BD,
∠DEG=∠HCG,
∴DE∥HC,
∴ ∠HCB = ∠EFB = 180° -(∠ABC+∠BEF)=90°,
∴∠ACH=∠HCB-∠ACB=x,
∴∠ACH=∠ABD.
∵CH=BD,AC=AB,
∴△ABD≌△ACH,
∴AD=AH.
∵DG=GH,
∴AG⊥GH.
2.证明:(1)设∠ABE=x.
∵AB=AC,AE=BE,∠BAC=90°
∴∠BAE=∠ABE=x,
∠ABC=∠ACB=45°.
∴∠GBC=∠ABC--∠ABE=45°-x,
∠AEG=∠ABE+∠AEB=2x.
∵AG⊥AE,
2x,
∴∠AGB=2∠GBC;
(2) 过点 C 作 HC∥AG,交 BG 于点H,连接AH,
∴∠AGB=∠CHG.
∵D 是 AC 的中点,
∴AD=CD,
又∵∠ADG=∠CDH,
∴△ADG≌△CDH,
∴AG=HC.
∵∠AGB=2∠GBC,∠CHG=∠HBC+∠HCB,
∴∠HBC=∠HCB,
∴BH=CH.
又∵AB=CA,
∴HA垂直平分BC,
∴∠BAH=∠CAH=45°.
又∵∠ABE=∠BAE,AB=BA,
∴△HAB≌△FBA(ASA),
∴AF=BH.
∵BH=HC,HC=AG,
∴AF=AG.
等腰三角形重难点突破
知等腰(一) 等边对等角
类型一 知等腰求角度
1.如图,以点 A 为圆心画弧,交直线 l于B,C两点,再分别以 A,B为圆心大于 AB 长为半径画弧交于M,N 两点,直线MN 交直线l 于点D,若 ,则∠CAD 的度数为( )
A.20° B.25° C.30° D.40°
2.如图,∠AOB=10°,射线OA,OB 上有一系列点( 且满足O n.当时,n的值为( )
A.6 B.7 C.8 D.9
类型二 隐等腰求角度
3.如图,在△ABC 中,BF 平分 交AC于点F,E 是AF 的中点,DE⊥AC交AB 于点D,连接DC 交BF于点P,则 的度数是( )
A.36° B.54° C.72° D.90°
类型三 知等腰证全等
4.如图,在. 中, D 是 BC 的中点,E 是 AC 的中点,连接AD,BE.
(1)求证:
(2)连接DE,求证:
知等腰(二)“三线合一”直接用
类型一 等腰+角平分线
1.如图,P 是△ABC 内部一点,且AC=BC,AP=BP,连接CP.若AB=3CP=3,求△APC的面积.
类型二 等腰十中线
2.如图,在△ABC 中,AB=AC,D 为BC 的中点,E 为AD 上一点,F 为BA 的延长线上一点,EF=EC.求证:∠CAF=∠CEF.
类型三 等腰十高
3.如图,在△ABC 中,AB=AC,AD⊥BC 于点D. G 为BC 的延长线上一点,过点G作AB 的垂线,垂足为E,交AD 于点F.若AF=FD,BC=2AE,求证:GF-AD=EF.
知等腰(三)“三线合一”连接用
类型一 连中线得垂直
1.如图,在等腰△ABC 中,AB=AC,D 为BC 的中点,E 为BD 上一点,CF⊥AE于点F.若EF=ED,求 的值.
2.如图,在△ABC 中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分別为 D,E.O为AB 的中点,连接OD,OE.求证:△ODE 为等腰直角三角形.
类型二 连中线得角平分线
3.如图,在△ABC 中,AB=AC,D 为BC 的中点,E,F 分别为AB,AC 上一点,∠EDF=2∠B.求证:DE=DF.
知等腰(四)“三线合一”构造用
类型一 知等腰→作“三线”
1.如图,在△ABC 中,AB=AC,作等腰△ACD,使得AC=CD.若∠ACD 与∠BAC 互补,过点 C 作CH⊥AD 于点H,求证:
2.如图,在△ABC 中,CE⊥AC 交AB 于点E,D 为CE 的延长线上一点,点 B在CD 的垂直平分线上.若BE=AE,EC=1,则DE的长为 .
3.如图,在△ABC中,AB=AC,E 为边AC 上一点,过点 C 作 BC 的垂线,交BE 的延长线于点D,连接AD.若∠DAC=∠ABD,求证:AE=EC.
类型二 构等腰→用“三线”
4.如图,在△ABC中,AB=AC,D 为△ABC 外一点,AE⊥BD 于点 E,∠BDC=∠BAC,DE=3,CD=2,则BE的长为 .
知等腰(五) 方程思想求角
类型一 多等腰
1.如图,在△ABC 中,边AB 和AC 的垂直平分线相交于边BC 上的点D,延长CB 到点E,使得 BE=AB,连接AE,∠E:∠C=5:8,则∠BAD 的度数为 .
2.如图,在等腰△ABC 中,AB=AC,线段 BD 把△ABC 分成了等腰△ABD 和等腰△BCD,且AD=BD,BC=DC.求∠A 的度数.
类型二 等腰+全等
3.如图,在△ABC中,点D,E 分别在BC 和AB 上.若AD=BD=AE,BE=DE=DC,则∠CAD的度数是 .
4.如图,在△ABC中,AD平分△ABC 的外角∠MAC,过点 C 作CE∥AB 交AD 于点E,点 F 在边AC上,且CF=AB.
(1)求证:EF=BC;
(2)若∠BCE=65°,∠AEF=2∠CEF,求∠BAC 的度数.
知等腰(六) 整体思想求角
类型一 共顶点三等腰
1如图,在四边形ABCD 中,AB=AC=AD,∠BAC=40°,则∠BDC 的度数为 .
2如图,点 D 在△ABC 内部,DB=DC,点E 在AB 上,DE 垂直平分AB.若∠ACB=75°,则∠BDE 的度数为 .
类型二 共底双等腰
3.如图,在△ABC 中,AB=AC,D 是△ABC 内部一点,DB=DC,E 是边AB上一点.若CD 平分∠ACE,∠AEC=100°,则∠BDC 的度数为 .
类型三 共顶点双等腰
4.如图,线段AB,DE 的垂直平分线交于点C,且∠ABC=∠CDE=78°,∠AEB=98°,则∠EBD 的度数为( )
A.162° B.152° C.122° D.112°
知等腰(七) 分类讨论求角
类型一 形状不明
1.在等腰△ABC中,AB=AC,两腰的垂直平分线交于点 P,已知∠BPC=90°,则等腰三角形的顶角度数为 .
2在△OPQ中,OP=OQ,OP 的垂直平分线交OP 于点D,交直线OQ于点E.若∠OEP=50°,则∠POQ的度数为 .
类型二 腰不明
3如图,在△ABC中,AB=BC,∠ABC=100°,AB 绕点B 顺时针旋转m°(0
类型一 三角形面积→高底关联
1.如图,已知AC⊥BC,AC=BC,BE⊥CD 于点E,AD⊥CE 于点D.
(1)求证:DE=BE--AD;
(2)O为AB 的中点,连接OD,OE,若AD=4,ED=7,求△OEB 的面积.
2.如图,在四边形ABCD 中,∠ABC=∠CAB=∠ADC=45°,△ACD 面积为12,且CD 的长为6.求△BCD 的面积.
3.如图,在四边形ABCD 中,AB=AC=AD,AB⊥AC,AE⊥BD 于点E.若BD=10,AE=3,求△BCD 的面积.
类型二 多边形面积→割补计算
4.如图,在五边形ABCDE 中,∠AED=90°,BC=DE,连接AC,AD,且AB=AD,AC⊥BC,∠ABC=∠CAD,F 为BE 的中点.
(1)求证:AF⊥CD;
(2)若AE=6,DE=4,则五边形ABCDE 的面积为 .
5.如图,在四边形 ABCD 中,∠BAD+∠BCD═180°,点 E 在CD 上,点 F 在AD上,AB=AF,CB=CE,M为EF 的中点.
(1)求证:CM⊥AM;
(2)若CM=4,AM=6,求五边形ABCEF 的面积.
6.如图,在五边形ABCDE 中,∠EAB=∠EDC=90°,AB=AE,DC=DE,AE
类型一 设参得等角证垂直
1.如图,在△ABC中,AB=AC,点 E 在AB 上,以 BE 为底边作等腰△DBE,取 CE 的中点G,连接AG,DG.若BE≠AE,∠BDE+∠BAC=180°,求证:AG⊥DG.
类型二 设参导倍角证全等
2.如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 在边AC 上,点 E 在线段BD上,连接AE,且AE=BE,延长AE交BC于点F,过点A 作AG⊥AE,交BD 的延长线于点 G.
(1)求证:∠AGB=2∠GBC;
(2)若 D 是AC 的中点,求证:AF=AG.
突破 5 知等腰(一)等边对等角
1. C 解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°.
∵MN 为AB 的垂直平分线,
∴DA=DB,
∴∠BAD=∠ABC=70°,
∴∠CAD=∠BAD-∠BAC=30°.
故选 C.
2. D
3. D 解:连接DF.
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°.
∵BF 平分∠ABC,
∴∠ABF=∠FBC=36°,
∴∠BFC=∠BCF=72°.
∵AE=EF,DE⊥AF,
∴AD=DF,
∴∠DFE=36°,
∴∠DFP=72°,
∴∠DFB=∠CFB.
∵BF=BF,∠DBF=∠CBF,
∴△BDF≌△CBF,
∴BD=BC.
∵BF 平分∠ABC,
∴BP⊥CD,
∴∠BPD=90°.选 D.
4.证明:(1)∵AC=BC,
∴∠BAC=∠ABC.
∵D,E 分别为BC,AC的中点,
∴BD=DC=AE=EC.
∵AB=AB,
∴△ABE≌△BAD,
∴∠BAD=∠ABE;
(2)延长 DE 至点F,使 EF=DE.
∵∠AEF=∠DEC,AE=EC,
∴△AEF≌△CED,
∴AF=CD=BD,∠F=∠EDC,
∴AF∥CD,
∴∠FAD=∠ADB.
∵AD=DA,
∴△FAD≌△BDA,
∴AB=DF=2DE.
突破 6 知等腰(二)“三线合一”直接用
1.解: 在△ACP 和△BCP 中,AC=BC,AP=BP,CP=CP,
∴△ACP≌△BCP,
∴∠ACP=∠BCP.
延长 CP 交AB 于点 D.
∵∠ACP=∠BCP,AC=BC,
∵AB=3CP=3,即CP=1,
2.证明:过点 E 作 EG⊥AB 于点 G,EH⊥AC 于点 H.
∵AB=AC,D为BC的中点,
∴AD平分∠BAC.
∵EG⊥AB,EH⊥AC,
∴EG=EH,
∠EGF=∠EHC=90°.
∵EF=EC,
∴Rt△EGF≌Rt△EHC,
∴∠F=∠ACE,
∴∠CAF=∠CEF.
3.证明:过点 D 作 DH⊥GE 于点 H.
∵GE⊥AB,
∴∠FEA=∠DHF=90°.
∵∠AFE=∠DFH,AF=DF,
∴△AEF≌△DHF,
∴HF=EF,AE=DH.
∵AD⊥BC,AB=AC,
∴BD=CD,∠BAD=∠CAD.
∵BC=2AE,
∴AE=DH=CD.
∵∠AEF=∠GDF=90°,∠AFE=∠GFD,
∴∠BAD=∠CAD=∠G.
∵∠ADC=∠DHG=90°,
∴△DGH≌△ACD,
∴GH=AD,
∴GF- AD = GF-GH = HF =EF.
突破7 知等腰(三)“三线合一”连接用
1.解:连接AD.
∵AB=AC,D 为BC的中点,
∴AD⊥BC,BD=CD.
∵∠AED=∠CEF,EF=ED,
∴△AED≌△CEF,
∴AE=EC=ED+CD.
∵AE=AF+EF,EF=ED,
∴AF=CD=BD,
2.证明:连接 OC,设AB 与CE 交于点F.可证△ACD≌△CBE,
∴DC=EB.
∵AC=BC,∠ACB=90°,
∴∠ABC=∠BAC=45°.
∵O为AB 的中点,
∴CO⊥AB,
∴∠BCO=∠ABC,
∴OC=OB.
∵BE⊥CE,CO⊥AB,
∴∠BEC=∠BOC=90°.
又 ∵ ∠BFC = ∠BOC + ∠1 =∠BEC+∠2,
∴∠1=∠2,
∴△DCO≌△EBO,
∴DO=EO,∠BOE=∠COD.
∵∠COD+∠DOB=90°,
∴∠BOE+∠DOB=90°,
∴∠DOE=90°.
又∵DO=EO,
∴△ODE 为等腰直角三角形.
3.证明:连接 AD,过点 D 作DM⊥AB于点 M,作 DN⊥AC 于点 N.
∵AB=AC,D 为BC的中点,
∴AD平分∠BAC,∠B=∠C.
∵DM⊥AB,DN⊥AC,
∴DM=DN.
∵∠BAC+∠B+∠C=180°,
∴2∠B+∠BAC=180°.
∵∠EDF=2∠B,
∴∠EDF+∠BAC=180°,
180°.
∵∠AED+∠DEM=180°,
∴∠AFD=∠DEM.
∵∠DME=∠DNF=90°,
∴△DEM≌△DFN,
∴DE=DF.
突破 8 知等腰(四)“三线合一”构造用
1.证明:过点 A 作AE⊥BC 于点E.
∵AB=AC,
∵AC=CD,CH⊥AD,
∠CAH+∠ACH=90°.
∵∠BAC+∠ACD=180°,
∠ACD)=90°,
∴∠EAC=∠CAH.
∵CE⊥AE,CH⊥AH,
2.3 解:过点 B 作 BM⊥DC 于点 M.
∵AC⊥CD,
∴∠BME=∠ACE=90°.
∵∠BEM=∠AEC,BE=AE,
∴△BME≌△ACE(AAS),
∴ME=CE=1.
∵点 B 在 CD 的垂直平分线上,
∴BD=BC.
∵BM⊥CD,
∴DM=MC=ME+EC=2,
∴DE=DM+ME=3.
3.证明:过点 A 作 AF⊥BC,交 BD 于点 F.
∵AB=AC,
∴∠BAF=∠CAB.
∵AF⊥BC,CD⊥BC,
∴AF∥CD,
∴∠ACD=∠CAF=∠BAF.
在△ABF 和△CAD 中,
∴△ABF≌△CAD(ASA),
∴AF=CD.
又 AF∥CD,
∴△AFE≌△CDE(AAS),
∴AE=EC.
4.5 解:在BD 上截取BF=CD,连接AF.设 BD 与AC 相交于点G.
∵∠BDC=∠BAC,
∠DGC=∠AGB,
∴∠ACD=∠ABF.
∵AB=AC,BF=CD,
∴△ABF≌△ACD,
∴AF=AD.
∵AE⊥BD,
∴FE=DE=3.
∵BF=CD=2,
∴BE=BF+FE=5.
突破 9 知等腰(五)方程思想求角
1.50° 解:设∠E=5x,则∠C=8x.
∵BE=BA,
∴∠BAE=∠E=5x.
由题意,得AD=CD,AD=DB,
∴∠C=∠DAC=8x,
∠DAB=∠DBA=2∠E=10x,
∴8x+8x+10x+10x=180°,
∴∠BAD=10x=50°.
2.解:设∠A=x.
∵AD=BD,
∴∠A=∠ABD=x,
∴∠BDC=∠A+∠ABD=2x.
∵BC=DC,
∴∠BDC=∠CBD=2x,
∴∠ABC=∠ACB=3x,
∴3x+3x+x=180°,
3.36° 解:设∠B=x.
∵BE=ED,AD=BD=AE,
∴∠EDB=∠DAB=∠B=x,
∴∠ADC=2x=∠AED=∠ADE,
∴5x=180°,
∴x=36°.
可证△ADC≌△ADE,
∴∠CAD=∠BAD=36°.
4.解:(1)∵AD 平分∠MAC,CE∥MB,
∴∠CEA=∠MAD=∠CAD,
∴CE=CA.
∵AB∥CE,
∴∠BAC=∠ECF.
∵AB=CF,
∴△ABC≌△CFE,
∴EF=BC;
(2)设∠BAC=x,则∠ECF=x,
∴∠ACB=∠BCE-∠ECF=65°-x.
∵△ABC≌△CFE,
∴∠CEF=∠ACB=65°-x,
∴∠AEF=2∠CEF=2(65°-x),
∵∠ECF + ∠CEA + ∠CAE =180°,
180°,
∴x=42°,
∴∠BAC=42°.
突破 10知等腰(六)整体思想求角
1.20° 解:设∠ABD=x.
∵AC=AB=AD,∠BAC=40°,
∴∠ABC=∠ACB=70°,∠ADB=∠ABD=x,
∴∠CAD=∠BAD-∠BAC=140°—2x.
∵AC=AD,
∴∠ACD=∠ADC=20°+x,
∴∠BDC=∠ADC-∠ADB=20°.
2.75° 解:连接AD.
∵DE 垂直平分AB,
∴AD=BD.
∵DB=DC,
∴CD=AD=BD,
∴ ∠DBC = ∠DCB,∠DAC =∠DCA,∠DAB=∠DBA.
∵∠ACB=75°,
∴∠DCB + ∠DCA = ∠DBC +∠DAC=75°,
∴∠DCB + ∠DCA + ∠DBC +∠DAC=150°,
30°,
∵AD=BD,DE⊥AB,
3.80° 解:设∠ACD =∠DCE=x,∠ECB=y.
∵AB=AC,DB=DC,
∴∠ABC=∠ACB=2x+y,∠DCB=∠DBC=x+y.
∵∠AEC=∠ECB+∠EBC=2x+2y,
∴2x+2y=100°,
4. C 解:连接CE,则CD=CE,CA=CB,
∴∠BAC=∠ABC=78°,∠CED=∠CDE=78°,
∴∠ACB=∠ECD=24°,
∴∠ACE=∠BCD,
∴△ACE≌△BCD,
∴∠AEC=∠BDC.设∠CEB=x,则∠AEC=∠AEB--∠CEB=98°-x,
∴∠BED=∠CED--∠CEB=78°-x.
∵△ACE≌△BCD,
∴∠BDE=∠CDE-∠CDB=78°
故选 C.
突破 11 知等腰(七)分类讨论求角
1.45°或135° 解:①当△ABC 为锐角三角形时,如图1,连接AP.
∵AP=BP=CP,
∴∠BAP=∠ABP,
∠CAP=∠ACP,
∴易证∠BPC=∠BAP+∠CAP+∠ACP+∠ABP=2∠BAC=90°,
∴∠BAC=45°;
②当△ABC 为钝角三角形时,如图2,连接AP.
∵AP=BP=CP,
∴∠BAP=∠ABP,∠CAP=∠ACP,
∴∠BAP + ∠CAP + ∠ACP +∠ABP=2∠BAC.
∵∠PBA + ∠PCA + ∠PAB +∠PAC+∠BPC=360°,∠BPC=90°,
∴∠BAC=135°.
故答案为 45°或 135°.
2.65°或115° 解:①如图1,当△OPQ为锐角三角形时,
∵DE 垂直且平分OP,
∴∠ODE=∠PDE=90°,OE=PE,
又∵∠OEP=50°,
∴∠OED=∠PED=25°,
65°;
②如图2,当△OPQ 为钝角三角形时,
∵DE 垂直且平分OP,
∴∠ODE=∠PDE=90°,OE=PE,
又∵∠OEP=50°,
∴∠OED=∠PED=25°,
综上,∠POQ=65°或115°.
3.100°或 130°或 160°
解:(1)若AD=AC.
∵AB=AB,BD=BC,
∴△ABD≌△ABC,
∴∠ABD=∠ABC=100°,
∴m=∠ABD=100°;
(2)若AD=DC.
∵DB=DB,AB=BC,
∴△ABD≌△CBD,
∠ABC)=130°,
∴m=130°;
(3)若CD=CA.
∵CB=CB,BA=BD,
∴△CBD≌△CBA,
∴∠CBD=∠CBA=100°,
160°.
故 m 的值为 100°或130°或 160°.
突破 12 知等腰(八) 巧算面积
1.解:(1)∵AC⊥BC,AD⊥CD,BE⊥CD,
∴∠ACB=∠ADC=∠BEC=90°,
∴ ∠ACD + ∠BCE = ∠CBE +∠BCE=90°,
∴∠ACD=∠CBE.
∵AC=BC,
∴△ACD≌△CBE,
∴AD=CE,BE=CD,
∴DE=CD-CE=BE-AD;
(2)延长 DO 交 BE 于点 F.
∵∠CEB=90°,
∴AD∥BE,
∴∠DAO=∠FBO,∠ADO=∠BFO.
∵O为AB 的中点,
∴AO=BO,
∴△AOD≌△BOF,
∴BF=AD,DO=OF.
由(1)知AD=CE,
∴CE=BF.
∵BE=CD,
∴EF=DE=7,
∴EO⊥ DF,∠DEO = ∠FEO =
∵OE⊥DF,
∴∠EOF=90°,
∴∠OFE=45°,
∴∠OEF=∠OFE,
∴OE=OF.过点 O 作OM⊥EB 于点M,
∴∠EOM =∠FOM=45°,∠OEF
=∠EOM=∠FOM=∠OFM,
2.解:过点 B 作 BM⊥DC 交 DC 的延长线于点M,过点 A 作AN⊥CD 于点 N,
12,
∴AN=4.
∵AN⊥CD,∠ADC=45°,
∴DN=AN=4,
∴CN=CD--ND=2.
∵∠ABC=∠CAB=45°,
∴∠BCA=90°,
∴∠BCM+∠ACN=90°.
∵AN⊥CD,
∴∠ANC=90°,
∴∠CAN+∠ACN=90°,
∴∠BCM=∠CAN.
∵∠M=∠ANC=90°,
∴△BCM≌△CAN,
∴BM=CN=2,
=6.
3.解:过点C 分别作CF⊥AE,交 AE的延长线于点 F,作 CG⊥BD 于点G.
∵AB=AD,AE⊥BD,
∵AB = AC,AB⊥AC,∠BAE+∠CAF=∠CAF+∠ACF,
∴∠BAE=∠ACF,
∴△ABE≌△CAF,
∴BE=AF=5,
∴EF=AF-AE=2.
∵CF∥BD,
∴CG=EF=2,
4.解:(1)延长AF,BC交于点G.
∵AB = AD, ∠AED =∠ACB =90°,BC=DE,
∴△ABC≌△ADE,
∴∠BAC=∠DAE.
又∵∠ABC=∠CAD,
∴∠CAE = ∠CAD + ∠DAE =∠ABC+∠BAC=90°=∠ACB,
∴BG∥AE,
∴∠G=∠EAG.
∵EF=BF,∠AFE=∠GFB,
∴△AEF≌△GBF,
∴AE=BG.
∵AC=AE,
∴BG=AC.
∴△ABG≌△DAC,
∴∠G=∠ACD.
∵∠ACG=∠ACB=90°,即∠ACD+∠GCD=90°
∴∠G+∠GCD=90°,
∴AF⊥CD;
(2)由(1)可知,BG=AC=AE=6, =18.
∵△ABG≌△DAC,
∴S△ACD=18.
12,
S△ADE=12+18+12=42.
5.解:(1)延长 CM 至点 G,使 GM=CM,连接GF,AC,AG.
∵FM=EM,∠FMG=∠EMC,MG=MC,
∴△FGM≌△ECM,
∴∠GFM=∠CEM,FG=EC.
∵CB=CE,
∴FG=BC.在五边形 ABCEF 中,∠B+∠BAD+∠BCD+∠CEM+∠EFA=540°.
∵∠BAD+∠BCD=180°,
∴∠B+∠CEM+∠EFA=360°,
∴∠B+∠GFM+∠EFA=360°.
∵∠AFG + ∠GFM + ∠EFA =360°,
∴∠B=∠GFA.
∵AF=AB,
∴△ABC≌△AFG,
∴AG=AC.
∵CM=MG,
∴AM⊥CM;
(2)∵△FGM≌△ECM,△ABC≌△AFG,
6.4.5 解:取 BC 的中点F,连接 AF并延长至点 G,使 FG=AF,连接DF,CG,DG.
可证△AFB ≌△GFC,△AED≌△GCD,
另解过 B,C,E 三点,分别作 AD 的垂线段,证全等.
突破 13 知等腰(九) 设参导角
1.证明:设∠BAC=2x,则.
∵BD=DE,
∴∠ABD=∠DEB=x.
∵AB=AC,
延长 ED 交 BC 于点 F,延长 DG 至点 H,使 GH=DG,连接 AD,AH,HC.
∵DG=GH,∠EGD=∠CGH,EG=GC,
∴△EGD≌△CGH,
∴CH=DE=BD,
∠DEG=∠HCG,
∴DE∥HC,
∴ ∠HCB = ∠EFB = 180° -(∠ABC+∠BEF)=90°,
∴∠ACH=∠HCB-∠ACB=x,
∴∠ACH=∠ABD.
∵CH=BD,AC=AB,
∴△ABD≌△ACH,
∴AD=AH.
∵DG=GH,
∴AG⊥GH.
2.证明:(1)设∠ABE=x.
∵AB=AC,AE=BE,∠BAC=90°
∴∠BAE=∠ABE=x,
∠ABC=∠ACB=45°.
∴∠GBC=∠ABC--∠ABE=45°-x,
∠AEG=∠ABE+∠AEB=2x.
∵AG⊥AE,
2x,
∴∠AGB=2∠GBC;
(2) 过点 C 作 HC∥AG,交 BG 于点H,连接AH,
∴∠AGB=∠CHG.
∵D 是 AC 的中点,
∴AD=CD,
又∵∠ADG=∠CDH,
∴△ADG≌△CDH,
∴AG=HC.
∵∠AGB=2∠GBC,∠CHG=∠HBC+∠HCB,
∴∠HBC=∠HCB,
∴BH=CH.
又∵AB=CA,
∴HA垂直平分BC,
∴∠BAH=∠CAH=45°.
又∵∠ABE=∠BAE,AB=BA,
∴△HAB≌△FBA(ASA),
∴AF=BH.
∵BH=HC,HC=AG,
∴AF=AG.
