全等三角形专项突破(含解析)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 全等三角形专项突破(含解析)2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 439.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
突破1 知全等(一) 求角度
类型一 对应角结合角平分线
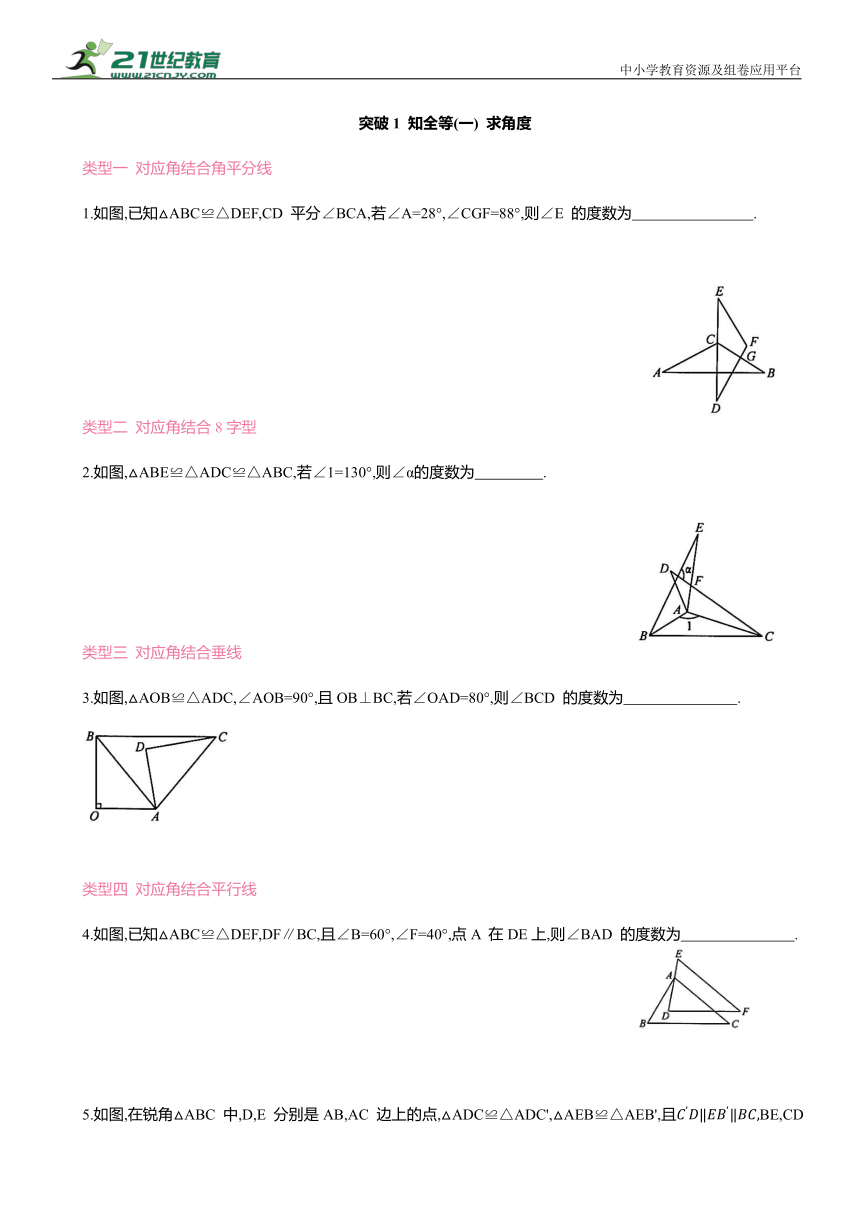
1.如图,已知△ABC≌△DEF,CD 平分∠BCA,若∠A=28°,∠CGF=88°,则∠E 的度数为 .
类型二 对应角结合8字型
2.如图,△ABE≌△ADC≌△ABC,若∠1=130°,则∠α的度数为 .
类型三 对应角结合垂线
3.如图,△AOB≌△ADC,∠AOB=90°,且OB⊥BC,若∠OAD=80°,则∠BCD 的度数为 .
类型四 对应角结合平行线
4.如图,已知△ABC≌△DEF,DF∥BC,且∠B=60°,∠F=40°,点A 在DE上,则∠BAD 的度数为 .
5.如图,在锐角△ABC 中,D,E 分别是AB,AC 边上的点,△ADC≌△ADC',△AEB≌△AEB',且BE,CD 交于点F.若∠BAC=35°,则∠BFC的度数是为 .
突破 2 知全等(二) 求长度
类型一 全等找准对应边
1.如图,△ABC 与△DEF 全等,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
类型二 对应边代换求长度
2.如图,在△ABC中,BC=6,AC=8,△DEF≌△ABC,且FE 和AC在同一直线上,若 FC=3.
(1)求 AE 的长;
(2)若AB 与 DE 相交于点 O,连接OC,S△ABC=24,OA=2OB,直接写出S△ OAE的值为 .
类型三 对应边代换算周长
3.如图,在三角形纸片 ABC 中, .沿过点B 的直线折叠这个三角形,使得点 C 落在AB 边上的点 E 处,折痕为 BD,则. 的周长为 .
4.如图,在 中,点D,点 E 分别在边 AB,BC 上,连接AE,DE,若 △BDE,AC:AB:BC=2:3:4,且△ABC的周长比 的周长大6.求 的周长.
类型四 对应边不确定
5.已知 的三边长分别为3,5,7, 的三边长分别为3,3x-2,2y-1,若这两个三角形全等,则x--y的值为 .
突破 1 知全等(一) 求角度
1.32° 解:∵△ABC≌△DEF,∠A=28°,
∴∠D=∠A=28°,∠B=∠E,
∴∠E+∠F=180°-∠D=180°-28°=152°.在四边形 ECGF 中,∠ECG=360°-∠CGF -(∠E +∠F)=360°-88°-152°=120°,
∴∠DCB=180°-∠ECG=180°-120°=60°.
∵CD平分∠BCA,
∴∠BCA=2∠DCB=120°,
∴∠E=∠B=180°-∠A-∠BCA=180°-28°-120°=32°.
2. 100° 解:∵△ABE≌△ADC≌△ABC,
∴∠BAE=∠1=130°,∠ACB=∠E,
∴∠2=360°-∠1-∠BAE=360°-130°-130°=100°,
∴∠DFE = 180°— ∠α — ∠E,∠AFC=180°-∠2-∠ACD.
∵∠DFE=∠AFC,
∴180°—∠α—∠E=180°—∠2—∠ACD,
∴∠α=∠2=100°.
3.10° 解:∵△AOB≌△ADC,
∴∠OAB=∠DAC.
∵∠OAD=∠DAB+∠OAB=80°,
∴∠BAC=∠DAB+∠DAC=80°.在△ABC 中,
∵∠ABC=∠ACB,
80°)=50°.
又∵∠AOB=90°,且OB⊥BC,
∴BC∥OA,
∴∠OAB=∠ABC=50°.
在△AOB 中,
∵∠O=90°,
∴∠ABO = ∠ACD = 90°- 50°=40°,
∴∠BCD=50°-40°=10°.
4.20° 解:∵△ABC≌△DEF,∴∠B=∠E=60°,∠C=∠F=40°.
∵DF∥BC,
∴∠1=∠C,
∴∠1=∠F,
∴AC∥EF,
∴∠2=∠E=60°.
∵∠BAC=180°-∠B-∠C=180°-60°-40°=80°,
∴∠BAD=∠BAC-∠2=80°-60°=20°.
5.110° 解:设∠C'=x,∠B'=y.
∵△ADC≌△ADC',
△AEB≌△AEB',
∠ABE = y,∠BAC =∠B'AC =35°,
∠BAC=∠C'AD=35°,
∴∠C'DB=∠C'+∠C'AD=35°+x,∠CEB'=∠B'+∠B'AC=35°+y.
∵C'D∥EB'∥BC,
∠BCE=∠CEB'=35°+y.
∵∠BAC + ∠DBC + ∠BCE =180°,
∴35°+35°+x+35°+y=180°,
∴x+y=75°,
∴∠ABE+∠ACD=x+y=75°,
∴∠FBC+∠FCB=180°--∠BAC
-(∠ABE+∠ACD)=70°,
∴ ∠BFC = 180°- (∠FBC +∠FCB)=110°.
突破 2 知全等(二) 求长度
1. A 解:由图中信息,得∠EDF 与∠A 为对应角,∴EF 与BC 为对应边,∴x=30.故选 A.
2.解:(1)∵BC=6,AC=8,
△DEF≌△ABC,
∴EF=BC=6.
∵FE 和AC 在同一直线上,FC=3,
∴AE=AC+EF--CF=8+6-3=11;
(2)∵S△ABC=24,OA=2OB,
∴S△ABC=3S△OBC,
∴S△OBC=8,S△OAC=16.
∵AE=11,AC=8,
3.7 cm 解:由折叠得 △BCD ≌△BED,
∴DE=DC,BE=BC=6cm,
∴AE=AB-BE=8-6=2( cm),
∴△AED 的周长=AD+DE+AE=AD+CD+AE=AC+AE=5+2=7( cm).
4.解:∵△ADE≌△BDE,
∴BE=AE,
∴C△AEC=AE+EC+AC=BE+EC+AC=BC+AC.
∵AC:AB: BC=2:3:4,
∴设AC=2x,AB=3x,BC=4x.
∵△ABC 的周长比△AEC 的周长大6,即C△ABC-C△AEC=6,
∴(AB+BC+AC) -(BC+AC)=6,
∴AB=3x=6,
∴x=2,
∴AC=2x=4,BC=4x=8,
∴C△AEC=BC+AC=8+4=12.
或 0 解:∵△ABC 与△DEF全等,
∴3x-2=5,2y-1=7,
或3x-2=7,2y-1=5,
解得 或x=3,y=3,
或 0.
故答案为 或 0.
突破1 知全等(一) 求角度
类型一 对应角结合角平分线
1.如图,已知△ABC≌△DEF,CD 平分∠BCA,若∠A=28°,∠CGF=88°,则∠E 的度数为 .
类型二 对应角结合8字型
2.如图,△ABE≌△ADC≌△ABC,若∠1=130°,则∠α的度数为 .
类型三 对应角结合垂线
3.如图,△AOB≌△ADC,∠AOB=90°,且OB⊥BC,若∠OAD=80°,则∠BCD 的度数为 .
类型四 对应角结合平行线
4.如图,已知△ABC≌△DEF,DF∥BC,且∠B=60°,∠F=40°,点A 在DE上,则∠BAD 的度数为 .
5.如图,在锐角△ABC 中,D,E 分别是AB,AC 边上的点,△ADC≌△ADC',△AEB≌△AEB',且BE,CD 交于点F.若∠BAC=35°,则∠BFC的度数是为 .
突破 2 知全等(二) 求长度
类型一 全等找准对应边
1.如图,△ABC 与△DEF 全等,则根据图中提供的信息,可得出x的值为( )
A.30 B.27 C.35 D.40
类型二 对应边代换求长度
2.如图,在△ABC中,BC=6,AC=8,△DEF≌△ABC,且FE 和AC在同一直线上,若 FC=3.
(1)求 AE 的长;
(2)若AB 与 DE 相交于点 O,连接OC,S△ABC=24,OA=2OB,直接写出S△ OAE的值为 .
类型三 对应边代换算周长
3.如图,在三角形纸片 ABC 中, .沿过点B 的直线折叠这个三角形,使得点 C 落在AB 边上的点 E 处,折痕为 BD,则. 的周长为 .
4.如图,在 中,点D,点 E 分别在边 AB,BC 上,连接AE,DE,若 △BDE,AC:AB:BC=2:3:4,且△ABC的周长比 的周长大6.求 的周长.
类型四 对应边不确定
5.已知 的三边长分别为3,5,7, 的三边长分别为3,3x-2,2y-1,若这两个三角形全等,则x--y的值为 .
突破 1 知全等(一) 求角度
1.32° 解:∵△ABC≌△DEF,∠A=28°,
∴∠D=∠A=28°,∠B=∠E,
∴∠E+∠F=180°-∠D=180°-28°=152°.在四边形 ECGF 中,∠ECG=360°-∠CGF -(∠E +∠F)=360°-88°-152°=120°,
∴∠DCB=180°-∠ECG=180°-120°=60°.
∵CD平分∠BCA,
∴∠BCA=2∠DCB=120°,
∴∠E=∠B=180°-∠A-∠BCA=180°-28°-120°=32°.
2. 100° 解:∵△ABE≌△ADC≌△ABC,
∴∠BAE=∠1=130°,∠ACB=∠E,
∴∠2=360°-∠1-∠BAE=360°-130°-130°=100°,
∴∠DFE = 180°— ∠α — ∠E,∠AFC=180°-∠2-∠ACD.
∵∠DFE=∠AFC,
∴180°—∠α—∠E=180°—∠2—∠ACD,
∴∠α=∠2=100°.
3.10° 解:∵△AOB≌△ADC,
∴∠OAB=∠DAC.
∵∠OAD=∠DAB+∠OAB=80°,
∴∠BAC=∠DAB+∠DAC=80°.在△ABC 中,
∵∠ABC=∠ACB,
80°)=50°.
又∵∠AOB=90°,且OB⊥BC,
∴BC∥OA,
∴∠OAB=∠ABC=50°.
在△AOB 中,
∵∠O=90°,
∴∠ABO = ∠ACD = 90°- 50°=40°,
∴∠BCD=50°-40°=10°.
4.20° 解:∵△ABC≌△DEF,∴∠B=∠E=60°,∠C=∠F=40°.
∵DF∥BC,
∴∠1=∠C,
∴∠1=∠F,
∴AC∥EF,
∴∠2=∠E=60°.
∵∠BAC=180°-∠B-∠C=180°-60°-40°=80°,
∴∠BAD=∠BAC-∠2=80°-60°=20°.
5.110° 解:设∠C'=x,∠B'=y.
∵△ADC≌△ADC',
△AEB≌△AEB',
∠ABE = y,∠BAC =∠B'AC =35°,
∠BAC=∠C'AD=35°,
∴∠C'DB=∠C'+∠C'AD=35°+x,∠CEB'=∠B'+∠B'AC=35°+y.
∵C'D∥EB'∥BC,
∠BCE=∠CEB'=35°+y.
∵∠BAC + ∠DBC + ∠BCE =180°,
∴35°+35°+x+35°+y=180°,
∴x+y=75°,
∴∠ABE+∠ACD=x+y=75°,
∴∠FBC+∠FCB=180°--∠BAC
-(∠ABE+∠ACD)=70°,
∴ ∠BFC = 180°- (∠FBC +∠FCB)=110°.
突破 2 知全等(二) 求长度
1. A 解:由图中信息,得∠EDF 与∠A 为对应角,∴EF 与BC 为对应边,∴x=30.故选 A.
2.解:(1)∵BC=6,AC=8,
△DEF≌△ABC,
∴EF=BC=6.
∵FE 和AC 在同一直线上,FC=3,
∴AE=AC+EF--CF=8+6-3=11;
(2)∵S△ABC=24,OA=2OB,
∴S△ABC=3S△OBC,
∴S△OBC=8,S△OAC=16.
∵AE=11,AC=8,
3.7 cm 解:由折叠得 △BCD ≌△BED,
∴DE=DC,BE=BC=6cm,
∴AE=AB-BE=8-6=2( cm),
∴△AED 的周长=AD+DE+AE=AD+CD+AE=AC+AE=5+2=7( cm).
4.解:∵△ADE≌△BDE,
∴BE=AE,
∴C△AEC=AE+EC+AC=BE+EC+AC=BC+AC.
∵AC:AB: BC=2:3:4,
∴设AC=2x,AB=3x,BC=4x.
∵△ABC 的周长比△AEC 的周长大6,即C△ABC-C△AEC=6,
∴(AB+BC+AC) -(BC+AC)=6,
∴AB=3x=6,
∴x=2,
∴AC=2x=4,BC=4x=8,
∴C△AEC=BC+AC=8+4=12.
或 0 解:∵△ABC 与△DEF全等,
∴3x-2=5,2y-1=7,
或3x-2=7,2y-1=5,
解得 或x=3,y=3,
或 0.
故答案为 或 0.
