等腰三角形模型重难点突破(含解析)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 等腰三角形模型重难点突破(含解析)2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
等腰三角形模型重难点突破
等腰模型(一) 手拉手
类型一 等腰直角三角形构手拉手
1.如图,在△ABC中,AC=BC,∠ACB=90°,E 为△ABC 外一点,∠AEB=90°,求∠AEC 的度数.
2如图,在五边形 AOBNM 中,AO=OB,MA=MN,∠AOB=∠AMN=90°,OM=8.求五边形 AOBNM 的面积.
类型二 等边三角形构手拉手
3.如图,△ABC 为等边三角形,D 为BC上一动点,M为AB 的延长线上一点,CD=BM. N为AD的中点,连接CN,MN.求证:MN⊥CN.
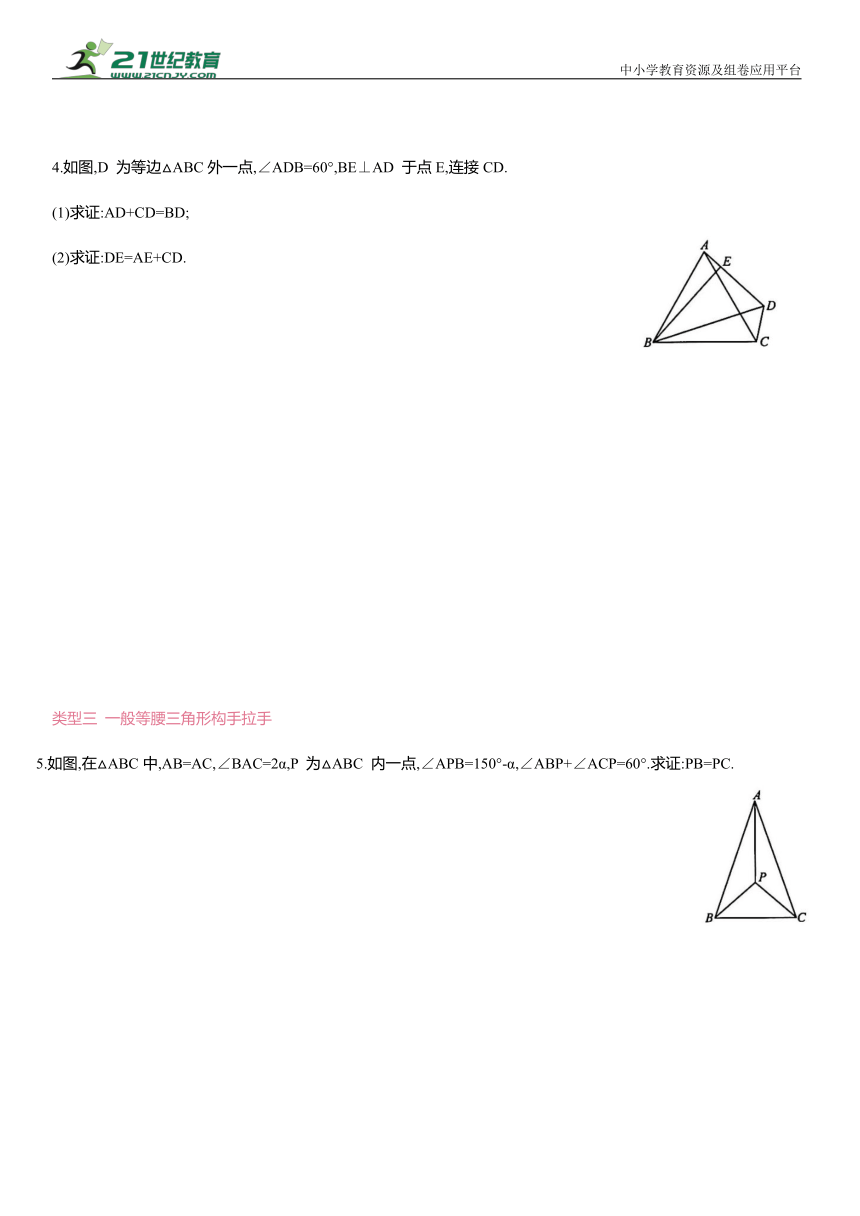
4.如图,D 为等边△ABC外一点,∠ADB=60°,BE⊥AD 于点E,连接CD.
(1)求证:AD+CD=BD;
(2)求证:DE=AE+CD.
类型三 一般等腰三角形构手拉手
5.如图,在△ABC中,AB=AC,∠BAC=2α,P 为△ABC 内一点,∠APB=150°-α,∠ABP+∠ACP=60°.求证:PB=PC.
等腰模型(二) 对角互补
类型一 90°对 90°
1.如图,在四边形 ABCD 中,∠BAD=∠BCD=90°,AB=AD,E 为BD上一点,∠BAE=∠DBC=22.5°.求证:BC=AE+CD.
类型二 60°对 120°
2.如图,在等边△ABC 中,D 是BC 边上的中点,E 为AB 的延长线上一点,F 为AC 上一点,∠EDF=120°,延长 DF,交 BA 的延长线于点 M.
(1)求证:ED=DF;
(2)若 BD=2AF,求证:AM=2BE.
3如图,在等边△ABC 中,E 为△ABC外一点,O 为BE 的中点,D 为AC 上一点,△DOE 为等边三角形,求证:OC=OD.
等腰模型(三) 一线三等角
类型一 等腰直角三角形背景
1.如图,△ABC 为等腰直角三角形,∠ABC=90°,△ABD 为等腰三角形,AD=AB=BC,E 为DB 延长线上一点,∠BAD=2∠CAE.若AE=a,BE=b,CE=c,则△ABC的面积为 .(用含a,b,c的式子表示)
类型二 等腰三角形背景
2.如图,△ABC 为等边三角形,直线l经过点C,在l上位于点C 右侧的点D 满足∠BDC=60°,点 F,G 在直线l上,连接AF,在l 上方作∠AFH=120°,且AF=HF,∠HGF=120°,求证:HG+BD=CF.
类型三 等边三角形背景
3.【问题情境】(1)如图1,△ABC 和△ADE 都是等边三角形,连接 BD,CE,求证:△ABD≌△ACE;
【迁移应用】(2)如图2,△ABC 和△ADE 都是等边三角形,A,B,E 三点在同一条直线上,M是AD 的中点,N 是AC 的中点,点 P 在BE 上,且△MNP 是等边三角形,求证:P 是 BE 的中点.
4.如图,在△ABC中,∠BAC=60°,D 是△ABC 外一点,△BCD 是等边三角形,过点 D 分别作AB,AC 的垂线,垂足分别为E,F,若CF=3BE,则 的值为( )
等腰模型(四) 夹半角
类型一 60°夹30°
1.如图,在等边△ABC 中,在AC 边上取点M,N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n 为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.随x,m,n 的值而定
类型二 120°夹60°
2.如图,在△ABC 中,∠BAC=120°,AB=AC,E,F 为BC 上两点,∠EAF=60°,∠AEF=75°,BE=10,求CF 的长.
类型三 90°夹 45°
3.如图,在△ABC中,AB=AC,∠BAC=90°. M,N为BC 上两点,∠AMN=75°,∠MAN=45°,探究 MN 与 CN 之间的数量关系.
4.如图,在△ABC中,AC=BC,∠ACB=90°,D 为AB 上一点,E 为AB 的延长线上一点,∠DCE=45°,∠CED=30°,求证:BD=BE.
等腰模型(五)“十字架”
类型一 等边三角形中的“十字架”
1.如图,在等边△ABC 中,D,E 分别为边AB,BC 上的点,AD=BE,AE 与CD 交于点 F.
(1)求证:△ABE≌△CAD;
(2)在 FC 上截取FG=AF,过点G 作GH∥BC 交AE 于点H.求证:GH=AD.
类型二 等腰三角形中的“十字架”
2.如图,在等腰△ABC中,AB=BC,∠BAC=30°,D,E,F 分别为线段AB,BC,AC 上的点,∠ABF=∠BED,DE 交BF 于点G.
(1)求∠BGD 的度数;
(2)若 BD=CE,点 H 在BF 的延长线上,BH=DE,连接AH.求证:AH∥BC.
等腰模型(六)“胖瘦三角形”
1如图,在△ABC中,AB=AC,点 E 在线段AC 上,点 D 在AB 的延长线上,连接DE 交 BC 于点 F,过点 E 作 EG⊥BC 于点G.
(1)若∠A=50°,∠D=30°,则∠GEF 的度数为 ;
(2)若BD=CE,求证:FG=BF+CG.
2.如图,在平面直角坐标系中,A(0,4),B(4,0),点M,N 分别在y轴和x 轴上,点N在点B 右侧,且AM=BN.连接MN交AB 的延长线于点C.求证:MC=CN.
3.如图,在△ABC 中,∠ABC=2∠ACB,BD 为△ABC 的角平分线.若 E 为线段BD 上一点,∠DEC=∠A,求证:AB=EC.
等腰模型(七)“镜面角”
类型一 反向延长构角平分线
1.如图,C 是等腰 Rt△OAB(OB=OA)中直角边 BO 延长线上的一点,过点 B 作 BD⊥AC 于点 D.若∠OAC=∠BAD,则 的值为( )
B.2
2.如图,在△ABD 中,E 为BA 的延长线上一点,DA=DE,点 F 在BD 上,且∠AFB=∠EFD,求证:∠FAD=∠FED.
类型二 作腰的平行线构双等腰
3.如图,在△ACE 中,AC=AE,延长 EC 至点B,BD⊥AE 交EA 的延长线于点D,若∠BAD=∠CAE,AB=6,AE=2,则AD 的长为 .
等腰模型(八) 角格点三角形
类型一 在60°角顶点处作等边构全等
1.如图,在四边形 ABCD 中,DB=DC,∠DCA=60°,∠DAC=78°,∠CAB=24°,则∠ACB 的度数为 .
2.如图,在△ABC 中,∠ABC=60°,∠ACB=80°,点D 在△ABC外,连接AD,BD,CD.若∠DBA=20°,∠ACD=30°,则∠BAD 的度数是( )
A.20° B.25° C.30° D.35°
类型二 无 60°角作等边构全等
3.如图,在△ABC 中,AC=AB=6,∠BAC=80°,O 为△ABC 内一点,∠OBC=10°,∠OCB=30°,则线段 BO 的长为 .
突破 34 等腰模型(一) 手拉手
1.解:过点 C 作 CF⊥CE 交 AE 于点F,设AE 与 BC 交于点D,
∴∠FCE=∠ACB=90°,
∴∠ACF=∠BCE.
∵∠AEB=∠ACB=90°,且∠ADC=∠BDE,
∴∠CAD=∠CBE.
∵AC=BC,
∴△ACF≌△BCE,
∴CF=CE.
∵∠FCE=90°,
∴∠AEC=∠CFE=45°.
2.解:过点 M 作 ME⊥OM,且 ME=OM=8,连接 NE,OE 交 BN 于点F,
∴∠OME=∠AMN=90°,
∴∠NME=∠AMO.
∵MA=MN,
∴△AMO≌△NME,
∴NE=OA=OB,∠MNE=∠A.
∵∠A+∠MNB+∠B+∠AMN+∠AOB=540°,∠AOB=∠AMN=90°,
∴∠MNE+∠MNB+∠B=360°.
∵∠MNE + ∠MNB + ∠ENB =360°,
∴∠B=∠ENB.
∵∠EFN=∠OFB,
∴△OBF≌△ENF,
∴S△ENF=S△OBF.
ME=32.
3.证明:延长 CN 至点 P,使 NP =CN,连接AP,MC,MP.
∵N 为AD 的中点,
∴AN=ND.
∵∠ANP=∠CND,
∴△ANP≌△DNC,
∴AP=CD,PN=NC,∠APN=∠NCD,
∴AP∥CB,
∴∠PAC+∠ACB=180°.
∵△ABC 为等边三角形,
∴AC=BC,∠ACB=∠ABC=60°,
∴∠PAC=∠CBM=120°.
∵CD=AP,CD=BM,
∴AP=BM,
∴△PAC≌△MBC,
∴MC=PC,∠PCA=∠MCB,
∴∠PCM=∠ACB=60°,
∴△PCM 为等边三角形,
∴PM=MC.
∵PN=NC,
∴MN⊥CN.
4.证明:(1)在 BD 上截取 DH=AD,连接AH.
∴△ADH 为等边三角形,
∴∠HAD=∠AHD=60°,AH=AD.
∵△ABC 为等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAC=∠HAD,
∴∠BAH=∠CAD,
∴△BAH≌△CAD,
∴BH=CD,
∴AD+CD=DH+BH=BD;
(2)在 ED 上截取 DM = DC,连接BM.
由(1)知△BAH≌△CAD,
∴ ∠ADC = ∠AHB = 180° -∠AHD=120°,
∴∠BDC=∠ADC--∠ADB=60°,
∴∠ADB=∠BDC.
∵DM=DC,DB=DB,
∴△BDM≌△BDC,
∴BC=BM.
∵AB=BC,
∴AB=BM.
∵BE⊥AD,
∴AE=EM,
∴DE=EM+DM=AE+CD.
5. 证明:在 AP 左 侧作 AE = AP,∠EAP =∠BAC= 2α,连接 EB,EP,
∴∠EAB=∠PAC.
∵AB=AC,
∴△AEB≌△APC,
∴EB=PC,∠ABE=∠ACP,
∴∠EBP = ∠ABE + ∠ABP =∠ACP+∠ABP=60°.
∵AP=AE,∠EAP=2α,
∴∠APE=∠AEP=90°-α,
∴ ∠EPB = ∠APB - ∠APE =
=60°,
∴∠BEP=∠EPB,
∴PB=EB,
∴PB=PC.
突破35 等腰模型(二)对角互补
1.证明:连接 AC,交 BD 于点 H,过点A 作AC 的垂线交CB 的延长线于点M.
∵∠BAD=∠BCD=90°,
-∠BCD=180°.
∵∠ABC+∠ABM=180°,
∴∠ABM=∠ADC.
∵∠MAC=∠BAD=90°,
∴∠MAB=∠CAD.
∵AB=AD,
∴△ABM≌△ADC,
∴AM=AC,
∴∠M=∠ACM=45°.
∵AB=AD,∠BAD=90°,
∴∠ABD=∠ADB=45°.
∵∠DBC=∠BAE=22.5°,
∴∠ABC=67.5°,
∠AED=∠BAE+∠ABD=67.5°,∠AHB=∠DBC+∠ACB=67.5°,
∴∠AED=∠AHE,
∴AE=AH,
∠CHD=∠AHB=67.5°.
∵∠BDC=90°-∠DBC=67.5°,
∴∠CHD=∠CDB,
∴CH=CD.
∵∠BAC=180°-∠ABC--∠ACB=67.5°,
∴∠ABC=∠BAC,
∴BC = AC = AH + CH = AE +CD.
2.证明:(1)取 AC 的中点 N,连接DN.
∵△ABC 为等边三角形,
∴AC=BC,∠ABC=∠C=60°.
∵D,N分别为BC,AC 的中点,
∴BD=CD=AN=CN,
∴△CDN 为等边三角形,
∴DN=CD=BD,∠CND=∠CDN=60°,
∴ ∠AND = ∠BDN = 120°=∠EDF=∠EBD,
∴∠EDB=∠FDN,
∴△EDB≌△FDN,
∴DE=DF;
(2)连接AD.
∵AB=AC,D 为BC的中点,
30°,
∴ ∠ADN = 180° ∠AND
∴∠DAN=∠ADN,
∴AN=DN.
∵BD=CD=CN=AN,BD=2AF,
∴AF=FN.
∠DNF=120°,
∴∠MAF=∠DNF.
∵∠AFM=∠DFN,
∴△AMF≌△NDF,
∴AM=DN.
∵DN=CN=AN,AN=2FN,
∴AM=DN=2FN.
由(1)知△EDB≌△FDN,
∴BE=FN,
∴AM=2BE.
3.证明:过点 O分别作OM⊥AC 于点M,ON⊥AB 于点 N,连接AO.
∵△ODE 为等边三角形,
∴∠DOE=60°,OD=OE,
∴∠BOD=120°.
∵O为BE 的中点,
∴OB=OE,
∴OD=OB.
∵△ABC 为等边三角形,
∴∠BAC=60°,
∴∠BOD+∠BAC=180°,
180°.
∵∠ODC+∠ADO=180°,
∴∠ABO=∠ODC.
∵ON⊥AB,OM⊥AC,
∴∠ONB=∠OMD=90°,
∴△ONB≌△OMD,
∴OM=ON,
∴AO平分∠BAC,
∴∠BAO=∠CAO.
∵AB=AC,AO=AO,
∴△ABO≌△ACO,
∴OC=OB.
∵OD=OE=OB,
∴OC=OD.
突破 36 等腰模型(三)一线三等角
解:过点 A,C分别作AF⊥DE,CG⊥DE,垂足分别为 F,G,
∴∠AFB=∠ABC=∠CGB=90°.
又∵AD=AB=BC,
∠BAD=2∠CAE,
∴∠BAC=∠ACB=45°,
∵∠ABC=90°,AF⊥DE,
∴∠FAB + ∠FBA = ∠FBA +∠CBG=90°,
∴∠FAB=∠CBG=∠CAE,∠AFB=∠CGB,AB=BC,
∴△BAF≌△CBG,
∴AF=BG,BF=CG.
∵∠CAE+∠BAE=45°,
∴∠FAB+∠BAE=45°,
∴∠AEF=∠FAE=45°,
∴AF=EF=BG.
又∵BF=CG,
∴BF=EG=CG,
∴∠CEG=∠AEF=45°,
∴∠AEC=90°,
∴CG=BF=EF-BE=AF-BE.
∵S△ABC=S△AEB+S△AEC=S△BEC,
b ).
2.证明:在l 上位于点C 左侧取一点E,
使∠AEC=60°,连接AE.
∵△ABC 是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠BCD+∠ACE=120°.
∵∠AEC=60°,
∴∠ACE+∠EAC=120°,
∴∠BCD=∠EAC.
∵∠AEC=∠BDC=60°,
∴△AEC≌△CDB,
∴BD=CE.
∵∠AEF=∠AFH=120°,
∴∠AFE + ∠FAE = ∠AFE +∠GFH=60°,
∴∠FAE=∠GFH.
∵∠HGF =∠AEF = 120°,AF =FH,
∴△HGF≌△FEA(AAS),
∴GH=EF,
∴CF=EF+CE=HG+BD.
3.证明:(1)∵△ABC 和△ADE 均为等边三角形,
∴AB=AC,AD=AE,
∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
∴△ABD≌△ACE;
(2)取 AE 的中点 K ,取 AB 的中点G,连接MK,NG.
∵M 为AD 的中点,N 为 AC 的中点,
AB=AC,AD=AE,
∴AN=AG,AM=AK.
∵∠CAB=∠DAE=60°,
∴△NAG 和△MAK 均为等边三角形.
∵△MPN 为等边三角形,
∴可证△MKP≌△PGN,
∴PK=NG=AG=BG,PG=MK=AK=EK,
∴EK+PK=PG+GB,
即EP=PB,
∴P 为EB 的中点.
4. A 解:过点 D 作直线 MN,点 M,N 分 别 在 射 线 AB, AC 上, 且∠AMN=60°.
∵∠A=60°,
∴△AMN 为等边三角形,
∴AM=AN=MN,∠ANM=60°.
∵△BCD 为等边三角形,
∴BC=CD=BD,∠BCD=∠CBD=∠BDC.
易证△ABC≌△MDB≌△NCD,
∴AC=BM=DN,CN=AB=MD.
设 BE=x,EM=y,
∵CF=3BE,
∴CF=3x,
∴BM=DN=AC=x+y,
AB=MD=CN=2y,
∴FN=CN-CF=2y-3x.
∵DN=2FN,
∴x+y=2(2y-3x)=4y-6x,
∴7x=3y,
∴AB=2y,AC=x+y= y,
选 A.
突破37 等腰模型(四) 夹半角
1. C 解:在 BC 下方作∠CBE =∠ABM,BE=BM,连接 NE,CE,则△CBE≌△ABM,
∴CE=AM=m,∠BCE=∠A=60°.由△MBN≌△EBN,得 NE=MN=x.
∵∠NCE = ∠ACB + ∠BCE =120°,
∴△NEC 为钝角三角形,选C.
2. 解: 将 △AEF 沿 AF 翻 折, 得△AGF, 连 接 CG, 则 △AEF ≌△AGF,
∴∠GAF =∠EAF =60°,∠AFG
∴∠CFG=∠EFG=90°,∠EAG=120°=∠BAC,
∴∠CAG=∠BAE.
∵AB=AC,AE=AG,
∴△ABE≌△ACG,
∴∠ACG=∠B=∠ACB=30°,
∴∠FCG=60°,
∴∠FGC=30°,
3.解:将△ABM 绕点 A 逆时针旋转90°,得到△ACD,连接DN,
则∠ACD=∠B=45°,
∠ADC=∠AMB=105°,
∴∠DCN=90°.
易证△AMN≌△ADN,
∴∠ADN=∠AMN=75°,DN=MN,
∴∠NDC = ∠ADC - ∠ADN =30°,
∴DN=2CN,
∴MN=2CN.
4.证明:过点 C 向右作CM⊥CD,CM=CD,连接 DM,BM,ME.
∵CA=CB,
∠DCE=45°,
∴∠ACD=∠BCM,∠MCE=45°,
∴△ACD≌△BCM,
∴∠MBC=∠CAD=45°,
∴∠MBA=90°,
∴∠MBE=90°.
∵CD=CM,CE=CE,
∴△CDE≌△CME,
∴∠MEC=∠CEB=30°,DE=ME,
∴△DME 是等边三角形.
又∵MB⊥DE,
∴BD=BE.
突破 38 等腰模型(五)“十字架”
1.证明:(1)∵△ABC为等边三角形,
∴AB=AC,∠ABC=∠BAC.
∵AD=BE,
∴△ABE≌△CAD;
(2)在 FH 上截取FM=FD.
∵∠AFD=∠GFM,AF=FG,
∴△AFD≌△GFM,
∴∠ADF=∠GMF,MG=AD.
∵△ABE≌△CAD,
∴∠ADC=∠AEB,
∴∠AEB=∠GMF,
∴∠AEC=∠GMH.
∵GH∥BC,
∴∠AHG=∠AEC,
∴∠AHG=∠GMH,
∴HG=GM,
∴HG=AD.
2.解:(1)∵AB=BC,
∴∠BAC=∠C=30°,
∴∠ABC=120°.
∵ ∠BGD = ∠GBE + ∠BED,∠ABF=∠BED,
∴∠BGD = ∠GBE + ∠ABF =∠ABC=120°;
(2)在 BA 上截取 BI = BE,连接IH.
∵BI=BE,∠IBH=∠BED,BH=DE,
∴△IBH≌△BED,
∴BD=IH,
∠BIH=∠EBD=120°,
∴∠AIH=60°.
∵BD=CE,AB=BC,
∴AD=BE,
∴BI=BE=AD,
∴AI=DB.
又∵BD=IH,
∴AI=IH,
∴△IAH 为等边三角形,
∴∠IAH=60°,
∴∠IAH+∠ABE=180°,
∴AH∥BC.
突破39 等腰模型(六)“胖瘦三角形”
1.解:(1)55°;
(2)过点 E 作 EH∥AB 交 BC 于点H,
则∠ABC=∠EHC,
∠D=∠FEH.
∵AB=AC,
∴∠ABC=∠C,
∴∠EHC=∠C,
∴EC=EH.
∵BD=CE,
∴BD=EH.
∵∠EFH=∠BFD,
∴△BDF≌△HEF(AAS),
∴BF=FH.
又∵EC=EH,EG⊥BC,
∴CG=HG,
∴FG=FH+HG=BF+CG.
2.证明:过点 M 作y 轴的垂线,交AB的延长线于点G.
∵A(0,4),B(4,0),∠AOB=90°,∠OAB=∠OBA=45°.
∵MG⊥y轴,
∴∠AMG=∠AOB=90°,
∴OB∥MG,
∴∠BNC=∠CMG,
∠G=∠OBA=45°,
∴∠MAG=∠G,
∴MG=AM=BN.
∵∠BCN=∠GCM,
∴△BCN≌△GCM,
∴MC=CN.
3.解:延长BD 到点T,使得CD=CT.
∵∠ABD=∠DBC=∠ACB,
∴BD=CD.
∵CD=CT,
∴∠T=∠CDT=∠ADB.
∵BD=CD,
∴BD=CT.
在△ABD 和△ECT 中,∠A=∠CET,∠ADB=∠T,BD=CT,
∴△ABD≌△ECT,
∴AB=EC.
突破 40 等腰模型(七)“镜面角”
1. B 解:延长 BD,OA 交于点 E,则∠BAD=∠OAC=∠EAD.
∵∠ADB=∠ADE=90°,
AD=AD,
∴△ADB≌△ADE,
∴BD=DE,
∴BE=2BD.
∵∠E=∠C,∠BOE=∠COA,OB=OA,
∴△BOE≌△AOC,
∴AC=BE=2BD,
选 B.
2.证明:过点 D 作 DM⊥EF 于点 M,DN⊥AF,交AF 的延长线于点 N.
∵∠AFB=∠DFN,
∠AFB=∠EFD,
∴∠DFN=∠EFD.
又∵DM⊥EF,DN⊥AF,
∴DM=DN.
在 Rt△DME 和 Rt△DNA 中,
DE=DA,DM=DN,
∴Rt△DME≌Rt△DNA,
∴∠DEM=∠DAN,
即∠FAD=∠FED.
3.2 解:过点 B 作 BG∥AC 交ED 的延长线于点G,
∴∠GBE=∠ACE,∠G=∠CAE.
∵AC=AE,∠BAD=∠CAE,
∴∠ACE=∠E,∠G=∠BAD,
∴∠GBE=∠GEB,BA=BG,
∴GE=BG=BA=6,
∴GA=GE--AE=4.
∵BA=BG,BD⊥DE,
突破 41 等腰模型(八)角格点三角形
1.18° 解:延长 CA 到点E,使 AE=AB,连接DE.
∵∠DAC=78°,
∴∠DAE=102°.
∵∠DAB=∠DAC+∠CAB=78°
∴∠DAE=∠DAB.
∵DA=DA,
∴△DAB≌△DAE(SAS),
∴DE=DB=DC.
∵∠DCA=60°,
∴△DEC 是等边三角形,
∴∠EDC=60°.
∴∠ADB=∠EDA=18°,
78°,
∴∠ACB=∠DCB-∠DCA=18°.
2. C 解:在AC 上取点E,使∠CBE=∠ABD=20°,连接DE.
∵∠ABC=60°,∠ACB=80°,
∴∠BAC=40°.
∵∠CBE=20°,∠ACB=80°,
∴∠BEC=80°,
∴BC=BE.
∵∠ACB=80°,∠ACD=30°,
∴∠BCD=50°.
∵∠ABC=60°,∠ABD=20°,
∴∠DBC=80°,
∴∠BDC=180°-∠DBC-∠BCD=50°,
∴∠BDC=∠BCD,
∴BD=BC,
∴BD=BE.
∵∠DBE=∠DBC-∠EBC=60°,
∴△DBE是等边三角形,
∴∠DEB=60°,DE=BE,
∴∠ABE=∠BEC-∠BAC=40°.
∵∠ABE=∠BAC=40°,
∴BE=AE=DE,
∴∠EAD=∠ADE.
∴∠DAE=70°,
∴∠BAD=∠DAE--∠BAC=30°.选 C.
3.6 解:在BC 上方作等边△DBC,连接 DA,AO,
∴DB=DC,∠BDC=60°.
∵AB=AC,DA=DA,
∴△DAB≌△DAC,
∴∠BDA=∠CDA,
∵∠BCO=30°,
∴∠BDA=∠BCO.
∵AB=AC,∠BAC=80°,
∴∠ABC=∠ACB=50°.
∵∠DBC=60°,∠OBC=10°,
∴∠DBA=10°,
∴∠DBA=∠OBC.
∵DB=BC,
∴△DBA≌△CBO,
∴OB=AB=6.
等腰三角形模型重难点突破
等腰模型(一) 手拉手
类型一 等腰直角三角形构手拉手
1.如图,在△ABC中,AC=BC,∠ACB=90°,E 为△ABC 外一点,∠AEB=90°,求∠AEC 的度数.
2如图,在五边形 AOBNM 中,AO=OB,MA=MN,∠AOB=∠AMN=90°,OM=8.求五边形 AOBNM 的面积.
类型二 等边三角形构手拉手
3.如图,△ABC 为等边三角形,D 为BC上一动点,M为AB 的延长线上一点,CD=BM. N为AD的中点,连接CN,MN.求证:MN⊥CN.
4.如图,D 为等边△ABC外一点,∠ADB=60°,BE⊥AD 于点E,连接CD.
(1)求证:AD+CD=BD;
(2)求证:DE=AE+CD.
类型三 一般等腰三角形构手拉手
5.如图,在△ABC中,AB=AC,∠BAC=2α,P 为△ABC 内一点,∠APB=150°-α,∠ABP+∠ACP=60°.求证:PB=PC.
等腰模型(二) 对角互补
类型一 90°对 90°
1.如图,在四边形 ABCD 中,∠BAD=∠BCD=90°,AB=AD,E 为BD上一点,∠BAE=∠DBC=22.5°.求证:BC=AE+CD.
类型二 60°对 120°
2.如图,在等边△ABC 中,D 是BC 边上的中点,E 为AB 的延长线上一点,F 为AC 上一点,∠EDF=120°,延长 DF,交 BA 的延长线于点 M.
(1)求证:ED=DF;
(2)若 BD=2AF,求证:AM=2BE.
3如图,在等边△ABC 中,E 为△ABC外一点,O 为BE 的中点,D 为AC 上一点,△DOE 为等边三角形,求证:OC=OD.
等腰模型(三) 一线三等角
类型一 等腰直角三角形背景
1.如图,△ABC 为等腰直角三角形,∠ABC=90°,△ABD 为等腰三角形,AD=AB=BC,E 为DB 延长线上一点,∠BAD=2∠CAE.若AE=a,BE=b,CE=c,则△ABC的面积为 .(用含a,b,c的式子表示)
类型二 等腰三角形背景
2.如图,△ABC 为等边三角形,直线l经过点C,在l上位于点C 右侧的点D 满足∠BDC=60°,点 F,G 在直线l上,连接AF,在l 上方作∠AFH=120°,且AF=HF,∠HGF=120°,求证:HG+BD=CF.
类型三 等边三角形背景
3.【问题情境】(1)如图1,△ABC 和△ADE 都是等边三角形,连接 BD,CE,求证:△ABD≌△ACE;
【迁移应用】(2)如图2,△ABC 和△ADE 都是等边三角形,A,B,E 三点在同一条直线上,M是AD 的中点,N 是AC 的中点,点 P 在BE 上,且△MNP 是等边三角形,求证:P 是 BE 的中点.
4.如图,在△ABC中,∠BAC=60°,D 是△ABC 外一点,△BCD 是等边三角形,过点 D 分别作AB,AC 的垂线,垂足分别为E,F,若CF=3BE,则 的值为( )
等腰模型(四) 夹半角
类型一 60°夹30°
1.如图,在等边△ABC 中,在AC 边上取点M,N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n 为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.随x,m,n 的值而定
类型二 120°夹60°
2.如图,在△ABC 中,∠BAC=120°,AB=AC,E,F 为BC 上两点,∠EAF=60°,∠AEF=75°,BE=10,求CF 的长.
类型三 90°夹 45°
3.如图,在△ABC中,AB=AC,∠BAC=90°. M,N为BC 上两点,∠AMN=75°,∠MAN=45°,探究 MN 与 CN 之间的数量关系.
4.如图,在△ABC中,AC=BC,∠ACB=90°,D 为AB 上一点,E 为AB 的延长线上一点,∠DCE=45°,∠CED=30°,求证:BD=BE.
等腰模型(五)“十字架”
类型一 等边三角形中的“十字架”
1.如图,在等边△ABC 中,D,E 分别为边AB,BC 上的点,AD=BE,AE 与CD 交于点 F.
(1)求证:△ABE≌△CAD;
(2)在 FC 上截取FG=AF,过点G 作GH∥BC 交AE 于点H.求证:GH=AD.
类型二 等腰三角形中的“十字架”
2.如图,在等腰△ABC中,AB=BC,∠BAC=30°,D,E,F 分别为线段AB,BC,AC 上的点,∠ABF=∠BED,DE 交BF 于点G.
(1)求∠BGD 的度数;
(2)若 BD=CE,点 H 在BF 的延长线上,BH=DE,连接AH.求证:AH∥BC.
等腰模型(六)“胖瘦三角形”
1如图,在△ABC中,AB=AC,点 E 在线段AC 上,点 D 在AB 的延长线上,连接DE 交 BC 于点 F,过点 E 作 EG⊥BC 于点G.
(1)若∠A=50°,∠D=30°,则∠GEF 的度数为 ;
(2)若BD=CE,求证:FG=BF+CG.
2.如图,在平面直角坐标系中,A(0,4),B(4,0),点M,N 分别在y轴和x 轴上,点N在点B 右侧,且AM=BN.连接MN交AB 的延长线于点C.求证:MC=CN.
3.如图,在△ABC 中,∠ABC=2∠ACB,BD 为△ABC 的角平分线.若 E 为线段BD 上一点,∠DEC=∠A,求证:AB=EC.
等腰模型(七)“镜面角”
类型一 反向延长构角平分线
1.如图,C 是等腰 Rt△OAB(OB=OA)中直角边 BO 延长线上的一点,过点 B 作 BD⊥AC 于点 D.若∠OAC=∠BAD,则 的值为( )
B.2
2.如图,在△ABD 中,E 为BA 的延长线上一点,DA=DE,点 F 在BD 上,且∠AFB=∠EFD,求证:∠FAD=∠FED.
类型二 作腰的平行线构双等腰
3.如图,在△ACE 中,AC=AE,延长 EC 至点B,BD⊥AE 交EA 的延长线于点D,若∠BAD=∠CAE,AB=6,AE=2,则AD 的长为 .
等腰模型(八) 角格点三角形
类型一 在60°角顶点处作等边构全等
1.如图,在四边形 ABCD 中,DB=DC,∠DCA=60°,∠DAC=78°,∠CAB=24°,则∠ACB 的度数为 .
2.如图,在△ABC 中,∠ABC=60°,∠ACB=80°,点D 在△ABC外,连接AD,BD,CD.若∠DBA=20°,∠ACD=30°,则∠BAD 的度数是( )
A.20° B.25° C.30° D.35°
类型二 无 60°角作等边构全等
3.如图,在△ABC 中,AC=AB=6,∠BAC=80°,O 为△ABC 内一点,∠OBC=10°,∠OCB=30°,则线段 BO 的长为 .
突破 34 等腰模型(一) 手拉手
1.解:过点 C 作 CF⊥CE 交 AE 于点F,设AE 与 BC 交于点D,
∴∠FCE=∠ACB=90°,
∴∠ACF=∠BCE.
∵∠AEB=∠ACB=90°,且∠ADC=∠BDE,
∴∠CAD=∠CBE.
∵AC=BC,
∴△ACF≌△BCE,
∴CF=CE.
∵∠FCE=90°,
∴∠AEC=∠CFE=45°.
2.解:过点 M 作 ME⊥OM,且 ME=OM=8,连接 NE,OE 交 BN 于点F,
∴∠OME=∠AMN=90°,
∴∠NME=∠AMO.
∵MA=MN,
∴△AMO≌△NME,
∴NE=OA=OB,∠MNE=∠A.
∵∠A+∠MNB+∠B+∠AMN+∠AOB=540°,∠AOB=∠AMN=90°,
∴∠MNE+∠MNB+∠B=360°.
∵∠MNE + ∠MNB + ∠ENB =360°,
∴∠B=∠ENB.
∵∠EFN=∠OFB,
∴△OBF≌△ENF,
∴S△ENF=S△OBF.
ME=32.
3.证明:延长 CN 至点 P,使 NP =CN,连接AP,MC,MP.
∵N 为AD 的中点,
∴AN=ND.
∵∠ANP=∠CND,
∴△ANP≌△DNC,
∴AP=CD,PN=NC,∠APN=∠NCD,
∴AP∥CB,
∴∠PAC+∠ACB=180°.
∵△ABC 为等边三角形,
∴AC=BC,∠ACB=∠ABC=60°,
∴∠PAC=∠CBM=120°.
∵CD=AP,CD=BM,
∴AP=BM,
∴△PAC≌△MBC,
∴MC=PC,∠PCA=∠MCB,
∴∠PCM=∠ACB=60°,
∴△PCM 为等边三角形,
∴PM=MC.
∵PN=NC,
∴MN⊥CN.
4.证明:(1)在 BD 上截取 DH=AD,连接AH.
∴△ADH 为等边三角形,
∴∠HAD=∠AHD=60°,AH=AD.
∵△ABC 为等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAC=∠HAD,
∴∠BAH=∠CAD,
∴△BAH≌△CAD,
∴BH=CD,
∴AD+CD=DH+BH=BD;
(2)在 ED 上截取 DM = DC,连接BM.
由(1)知△BAH≌△CAD,
∴ ∠ADC = ∠AHB = 180° -∠AHD=120°,
∴∠BDC=∠ADC--∠ADB=60°,
∴∠ADB=∠BDC.
∵DM=DC,DB=DB,
∴△BDM≌△BDC,
∴BC=BM.
∵AB=BC,
∴AB=BM.
∵BE⊥AD,
∴AE=EM,
∴DE=EM+DM=AE+CD.
5. 证明:在 AP 左 侧作 AE = AP,∠EAP =∠BAC= 2α,连接 EB,EP,
∴∠EAB=∠PAC.
∵AB=AC,
∴△AEB≌△APC,
∴EB=PC,∠ABE=∠ACP,
∴∠EBP = ∠ABE + ∠ABP =∠ACP+∠ABP=60°.
∵AP=AE,∠EAP=2α,
∴∠APE=∠AEP=90°-α,
∴ ∠EPB = ∠APB - ∠APE =
=60°,
∴∠BEP=∠EPB,
∴PB=EB,
∴PB=PC.
突破35 等腰模型(二)对角互补
1.证明:连接 AC,交 BD 于点 H,过点A 作AC 的垂线交CB 的延长线于点M.
∵∠BAD=∠BCD=90°,
-∠BCD=180°.
∵∠ABC+∠ABM=180°,
∴∠ABM=∠ADC.
∵∠MAC=∠BAD=90°,
∴∠MAB=∠CAD.
∵AB=AD,
∴△ABM≌△ADC,
∴AM=AC,
∴∠M=∠ACM=45°.
∵AB=AD,∠BAD=90°,
∴∠ABD=∠ADB=45°.
∵∠DBC=∠BAE=22.5°,
∴∠ABC=67.5°,
∠AED=∠BAE+∠ABD=67.5°,∠AHB=∠DBC+∠ACB=67.5°,
∴∠AED=∠AHE,
∴AE=AH,
∠CHD=∠AHB=67.5°.
∵∠BDC=90°-∠DBC=67.5°,
∴∠CHD=∠CDB,
∴CH=CD.
∵∠BAC=180°-∠ABC--∠ACB=67.5°,
∴∠ABC=∠BAC,
∴BC = AC = AH + CH = AE +CD.
2.证明:(1)取 AC 的中点 N,连接DN.
∵△ABC 为等边三角形,
∴AC=BC,∠ABC=∠C=60°.
∵D,N分别为BC,AC 的中点,
∴BD=CD=AN=CN,
∴△CDN 为等边三角形,
∴DN=CD=BD,∠CND=∠CDN=60°,
∴ ∠AND = ∠BDN = 120°=∠EDF=∠EBD,
∴∠EDB=∠FDN,
∴△EDB≌△FDN,
∴DE=DF;
(2)连接AD.
∵AB=AC,D 为BC的中点,
30°,
∴ ∠ADN = 180° ∠AND
∴∠DAN=∠ADN,
∴AN=DN.
∵BD=CD=CN=AN,BD=2AF,
∴AF=FN.
∠DNF=120°,
∴∠MAF=∠DNF.
∵∠AFM=∠DFN,
∴△AMF≌△NDF,
∴AM=DN.
∵DN=CN=AN,AN=2FN,
∴AM=DN=2FN.
由(1)知△EDB≌△FDN,
∴BE=FN,
∴AM=2BE.
3.证明:过点 O分别作OM⊥AC 于点M,ON⊥AB 于点 N,连接AO.
∵△ODE 为等边三角形,
∴∠DOE=60°,OD=OE,
∴∠BOD=120°.
∵O为BE 的中点,
∴OB=OE,
∴OD=OB.
∵△ABC 为等边三角形,
∴∠BAC=60°,
∴∠BOD+∠BAC=180°,
180°.
∵∠ODC+∠ADO=180°,
∴∠ABO=∠ODC.
∵ON⊥AB,OM⊥AC,
∴∠ONB=∠OMD=90°,
∴△ONB≌△OMD,
∴OM=ON,
∴AO平分∠BAC,
∴∠BAO=∠CAO.
∵AB=AC,AO=AO,
∴△ABO≌△ACO,
∴OC=OB.
∵OD=OE=OB,
∴OC=OD.
突破 36 等腰模型(三)一线三等角
解:过点 A,C分别作AF⊥DE,CG⊥DE,垂足分别为 F,G,
∴∠AFB=∠ABC=∠CGB=90°.
又∵AD=AB=BC,
∠BAD=2∠CAE,
∴∠BAC=∠ACB=45°,
∵∠ABC=90°,AF⊥DE,
∴∠FAB + ∠FBA = ∠FBA +∠CBG=90°,
∴∠FAB=∠CBG=∠CAE,∠AFB=∠CGB,AB=BC,
∴△BAF≌△CBG,
∴AF=BG,BF=CG.
∵∠CAE+∠BAE=45°,
∴∠FAB+∠BAE=45°,
∴∠AEF=∠FAE=45°,
∴AF=EF=BG.
又∵BF=CG,
∴BF=EG=CG,
∴∠CEG=∠AEF=45°,
∴∠AEC=90°,
∴CG=BF=EF-BE=AF-BE.
∵S△ABC=S△AEB+S△AEC=S△BEC,
b ).
2.证明:在l 上位于点C 左侧取一点E,
使∠AEC=60°,连接AE.
∵△ABC 是等边三角形,
∴AC=BC,∠ACB=60°,
∴∠BCD+∠ACE=120°.
∵∠AEC=60°,
∴∠ACE+∠EAC=120°,
∴∠BCD=∠EAC.
∵∠AEC=∠BDC=60°,
∴△AEC≌△CDB,
∴BD=CE.
∵∠AEF=∠AFH=120°,
∴∠AFE + ∠FAE = ∠AFE +∠GFH=60°,
∴∠FAE=∠GFH.
∵∠HGF =∠AEF = 120°,AF =FH,
∴△HGF≌△FEA(AAS),
∴GH=EF,
∴CF=EF+CE=HG+BD.
3.证明:(1)∵△ABC 和△ADE 均为等边三角形,
∴AB=AC,AD=AE,
∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
∴△ABD≌△ACE;
(2)取 AE 的中点 K ,取 AB 的中点G,连接MK,NG.
∵M 为AD 的中点,N 为 AC 的中点,
AB=AC,AD=AE,
∴AN=AG,AM=AK.
∵∠CAB=∠DAE=60°,
∴△NAG 和△MAK 均为等边三角形.
∵△MPN 为等边三角形,
∴可证△MKP≌△PGN,
∴PK=NG=AG=BG,PG=MK=AK=EK,
∴EK+PK=PG+GB,
即EP=PB,
∴P 为EB 的中点.
4. A 解:过点 D 作直线 MN,点 M,N 分 别 在 射 线 AB, AC 上, 且∠AMN=60°.
∵∠A=60°,
∴△AMN 为等边三角形,
∴AM=AN=MN,∠ANM=60°.
∵△BCD 为等边三角形,
∴BC=CD=BD,∠BCD=∠CBD=∠BDC.
易证△ABC≌△MDB≌△NCD,
∴AC=BM=DN,CN=AB=MD.
设 BE=x,EM=y,
∵CF=3BE,
∴CF=3x,
∴BM=DN=AC=x+y,
AB=MD=CN=2y,
∴FN=CN-CF=2y-3x.
∵DN=2FN,
∴x+y=2(2y-3x)=4y-6x,
∴7x=3y,
∴AB=2y,AC=x+y= y,
选 A.
突破37 等腰模型(四) 夹半角
1. C 解:在 BC 下方作∠CBE =∠ABM,BE=BM,连接 NE,CE,则△CBE≌△ABM,
∴CE=AM=m,∠BCE=∠A=60°.由△MBN≌△EBN,得 NE=MN=x.
∵∠NCE = ∠ACB + ∠BCE =120°,
∴△NEC 为钝角三角形,选C.
2. 解: 将 △AEF 沿 AF 翻 折, 得△AGF, 连 接 CG, 则 △AEF ≌△AGF,
∴∠GAF =∠EAF =60°,∠AFG
∴∠CFG=∠EFG=90°,∠EAG=120°=∠BAC,
∴∠CAG=∠BAE.
∵AB=AC,AE=AG,
∴△ABE≌△ACG,
∴∠ACG=∠B=∠ACB=30°,
∴∠FCG=60°,
∴∠FGC=30°,
3.解:将△ABM 绕点 A 逆时针旋转90°,得到△ACD,连接DN,
则∠ACD=∠B=45°,
∠ADC=∠AMB=105°,
∴∠DCN=90°.
易证△AMN≌△ADN,
∴∠ADN=∠AMN=75°,DN=MN,
∴∠NDC = ∠ADC - ∠ADN =30°,
∴DN=2CN,
∴MN=2CN.
4.证明:过点 C 向右作CM⊥CD,CM=CD,连接 DM,BM,ME.
∵CA=CB,
∠DCE=45°,
∴∠ACD=∠BCM,∠MCE=45°,
∴△ACD≌△BCM,
∴∠MBC=∠CAD=45°,
∴∠MBA=90°,
∴∠MBE=90°.
∵CD=CM,CE=CE,
∴△CDE≌△CME,
∴∠MEC=∠CEB=30°,DE=ME,
∴△DME 是等边三角形.
又∵MB⊥DE,
∴BD=BE.
突破 38 等腰模型(五)“十字架”
1.证明:(1)∵△ABC为等边三角形,
∴AB=AC,∠ABC=∠BAC.
∵AD=BE,
∴△ABE≌△CAD;
(2)在 FH 上截取FM=FD.
∵∠AFD=∠GFM,AF=FG,
∴△AFD≌△GFM,
∴∠ADF=∠GMF,MG=AD.
∵△ABE≌△CAD,
∴∠ADC=∠AEB,
∴∠AEB=∠GMF,
∴∠AEC=∠GMH.
∵GH∥BC,
∴∠AHG=∠AEC,
∴∠AHG=∠GMH,
∴HG=GM,
∴HG=AD.
2.解:(1)∵AB=BC,
∴∠BAC=∠C=30°,
∴∠ABC=120°.
∵ ∠BGD = ∠GBE + ∠BED,∠ABF=∠BED,
∴∠BGD = ∠GBE + ∠ABF =∠ABC=120°;
(2)在 BA 上截取 BI = BE,连接IH.
∵BI=BE,∠IBH=∠BED,BH=DE,
∴△IBH≌△BED,
∴BD=IH,
∠BIH=∠EBD=120°,
∴∠AIH=60°.
∵BD=CE,AB=BC,
∴AD=BE,
∴BI=BE=AD,
∴AI=DB.
又∵BD=IH,
∴AI=IH,
∴△IAH 为等边三角形,
∴∠IAH=60°,
∴∠IAH+∠ABE=180°,
∴AH∥BC.
突破39 等腰模型(六)“胖瘦三角形”
1.解:(1)55°;
(2)过点 E 作 EH∥AB 交 BC 于点H,
则∠ABC=∠EHC,
∠D=∠FEH.
∵AB=AC,
∴∠ABC=∠C,
∴∠EHC=∠C,
∴EC=EH.
∵BD=CE,
∴BD=EH.
∵∠EFH=∠BFD,
∴△BDF≌△HEF(AAS),
∴BF=FH.
又∵EC=EH,EG⊥BC,
∴CG=HG,
∴FG=FH+HG=BF+CG.
2.证明:过点 M 作y 轴的垂线,交AB的延长线于点G.
∵A(0,4),B(4,0),∠AOB=90°,∠OAB=∠OBA=45°.
∵MG⊥y轴,
∴∠AMG=∠AOB=90°,
∴OB∥MG,
∴∠BNC=∠CMG,
∠G=∠OBA=45°,
∴∠MAG=∠G,
∴MG=AM=BN.
∵∠BCN=∠GCM,
∴△BCN≌△GCM,
∴MC=CN.
3.解:延长BD 到点T,使得CD=CT.
∵∠ABD=∠DBC=∠ACB,
∴BD=CD.
∵CD=CT,
∴∠T=∠CDT=∠ADB.
∵BD=CD,
∴BD=CT.
在△ABD 和△ECT 中,∠A=∠CET,∠ADB=∠T,BD=CT,
∴△ABD≌△ECT,
∴AB=EC.
突破 40 等腰模型(七)“镜面角”
1. B 解:延长 BD,OA 交于点 E,则∠BAD=∠OAC=∠EAD.
∵∠ADB=∠ADE=90°,
AD=AD,
∴△ADB≌△ADE,
∴BD=DE,
∴BE=2BD.
∵∠E=∠C,∠BOE=∠COA,OB=OA,
∴△BOE≌△AOC,
∴AC=BE=2BD,
选 B.
2.证明:过点 D 作 DM⊥EF 于点 M,DN⊥AF,交AF 的延长线于点 N.
∵∠AFB=∠DFN,
∠AFB=∠EFD,
∴∠DFN=∠EFD.
又∵DM⊥EF,DN⊥AF,
∴DM=DN.
在 Rt△DME 和 Rt△DNA 中,
DE=DA,DM=DN,
∴Rt△DME≌Rt△DNA,
∴∠DEM=∠DAN,
即∠FAD=∠FED.
3.2 解:过点 B 作 BG∥AC 交ED 的延长线于点G,
∴∠GBE=∠ACE,∠G=∠CAE.
∵AC=AE,∠BAD=∠CAE,
∴∠ACE=∠E,∠G=∠BAD,
∴∠GBE=∠GEB,BA=BG,
∴GE=BG=BA=6,
∴GA=GE--AE=4.
∵BA=BG,BD⊥DE,
突破 41 等腰模型(八)角格点三角形
1.18° 解:延长 CA 到点E,使 AE=AB,连接DE.
∵∠DAC=78°,
∴∠DAE=102°.
∵∠DAB=∠DAC+∠CAB=78°
∴∠DAE=∠DAB.
∵DA=DA,
∴△DAB≌△DAE(SAS),
∴DE=DB=DC.
∵∠DCA=60°,
∴△DEC 是等边三角形,
∴∠EDC=60°.
∴∠ADB=∠EDA=18°,
78°,
∴∠ACB=∠DCB-∠DCA=18°.
2. C 解:在AC 上取点E,使∠CBE=∠ABD=20°,连接DE.
∵∠ABC=60°,∠ACB=80°,
∴∠BAC=40°.
∵∠CBE=20°,∠ACB=80°,
∴∠BEC=80°,
∴BC=BE.
∵∠ACB=80°,∠ACD=30°,
∴∠BCD=50°.
∵∠ABC=60°,∠ABD=20°,
∴∠DBC=80°,
∴∠BDC=180°-∠DBC-∠BCD=50°,
∴∠BDC=∠BCD,
∴BD=BC,
∴BD=BE.
∵∠DBE=∠DBC-∠EBC=60°,
∴△DBE是等边三角形,
∴∠DEB=60°,DE=BE,
∴∠ABE=∠BEC-∠BAC=40°.
∵∠ABE=∠BAC=40°,
∴BE=AE=DE,
∴∠EAD=∠ADE.
∴∠DAE=70°,
∴∠BAD=∠DAE--∠BAC=30°.选 C.
3.6 解:在BC 上方作等边△DBC,连接 DA,AO,
∴DB=DC,∠BDC=60°.
∵AB=AC,DA=DA,
∴△DAB≌△DAC,
∴∠BDA=∠CDA,
∵∠BCO=30°,
∴∠BDA=∠BCO.
∵AB=AC,∠BAC=80°,
∴∠ABC=∠ACB=50°.
∵∠DBC=60°,∠OBC=10°,
∴∠DBA=10°,
∴∠DBA=∠OBC.
∵DB=BC,
∴△DBA≌△CBO,
∴OB=AB=6.
